Similar presentations:
Законы и основные уравнения электромагнитного поля. Тема № 2
1. МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ ИРКУТСКИЙ ФИЛИАЛ КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТГРАЖДАНСКОЙ АВИАЦИИ
ИРКУТСКИЙ ФИЛИАЛ
КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И ПИЛОТАЖНОНАВИГАЦИОННЫХ КОМПЛЕКСОВ
ЛЕКЦИЯ № 2.3
по дисциплине
Теория электромагнитного поля
ТЕМА № 2
Законы и основные уравнения электромагнитного
поля
2. Вопросы лекции
15Вопросы лекции
2.2. Постоянный ток:
2.2.1. Ток и плотность тока проводимости.
2.2.2. Закон Ома в дифференциальной форме.
2.2.3. Закон Джоуля –Ленца в дифференциальной форме.
2.2.4. Первый закон Кирхгофа в дифференциальной
форме.
2.2.5. Граничные условия.
3. 2.2. Постоянный ток: 2.2.1. Ток и плотность тока проводимости.
14Если в проводнике существует электрическое поле, оно вызывает
упорядоченное движение зарядов, представляющее собой ток проводимости. В
металлических проводниках ток проводимости определяется движением
электронов. Мерой тока служит предел отношения заряда q, проходящего
сквозь заданную поверхность в течение некоторого времени t, к величине t,
когда t стремится к нулю как к пределу:
dq dq
t 0 dt
dt
i lim
Ток – величина скалярная. Если значение тока не зависит от времени, ток
называется постоянным. Ток измеряется в амперах (А). Плотностью тока
называют векторную величину , численное значение которой равно пределу
отношения тока, протекающего через некоторую площадку, расположенную
нормально к направлению движения зарядов, к величине площади этой
площадки, когда она стремится к нулю как к пределу:
di
di
lim
Sn 0 dS
dSn
n
4.
Направление вектора (дельта) выбирается таким образом, чтобы оно13
совпадало с направлением движения положительных зарядов (или было
противоположно направлению движения отрицательных зарядов). Ток и
плотность тока связаны соотношением
(1)
i dS .
S
Ток сквозь поверхность S равен потоку вектора плотности тока сквозь ту же
поверхность. Плотность тока измеряется в амперах на квадратный метр (А/м2).
При постоянном токе распределение зарядов в проводнике не изменяется во
времени. Поле таких зарядов такое же, как и в случае неподвижных зарядов,
равных по величине и знаку и распределенных так же.
5. 2.2.2. Закон Ома в дифференциальной форме.
12В однородном (состоящем из одного и того же вещества) изотропном (не
зависящем от направления действия векторов Е и ) проводнике плотность тока
проводимости пропорциональна
напряженности электрического поля Е
(2)
E .
Формула (2) выражает связь между плотностью тока проводимости и
напряженностью электрического поля в данной точке проводящей среды и
представляет собой закон Ома в дифференциальной форме. Коэффициент
называется удельной проводимостью и измеряется в Сим/м.
Если в электростатическое поле внести проводник, то в нем произойдет
перемещение зарядов. Заряды эти распределятся таким образом, что поле,
созданное ими, скомпенсирует внешнее поле. Для того чтобы в проводнике
длительно проходил ток, необходимо наличие электрического поля, силы
которого перемещают заряды. Такое поле может быть создано и будет
поддерживаться процессами неэлектростатического происхождения
(химическими, термоэлектрическими и др.) и носит название стороннего
электрического поля.
Так как при прохождении тока по проводнику все время происходит
преобразование электрической энергии в тепловую, энергия поля должна
непрерывно пополняться за счет внешнего источника. Только при этом условии
может длительно существовать ток.
6.
Следовательно, стороннее поле всегда связано с источником энергии,который преобразует какую-либо форму энергии (химическую, тепловую,
механическую) в энергию электрическую и поддерживает ток в проводнике.
Напряженность стороннего электрического поля обозначают Естор. Если на
заряд q в проводнике действует сторонняя сила Fстор, то
E стор lim
Fстор
q 0
q
11
.
Если в проводнике одновременно действуют и электростатические и
сторонние силы, напряженность результирующего поля равна:
Ерез= Е-Естор.
Линейный интеграл напряженности стороннего поля между двумя точками а
и b заданного пути интегрирования а – 1 - b называют электродвижущей
силой (э. д. с.)
e a1b E стор dl
a1b
.
Если путь интегрирования замкнут, то величина
ea1b E стор dl
L
называется э. д. с, действующей в контуре L.
(3)
7.
Линейный интеграл напряженности результирующего поля называетсянапряжением вдоль пути интегрирования или падением напряжения на
этом участке
u a1b E резdl
a1b
Величины напряжения и э.д.с. зависят от выбора пути интегрирования.
Напомним, что в электростатическом поле
Edl 0,
b
Edl
L
а линейный интеграл a
не зависит от выбора пути интегрирования. Он
равен разности потенциалов начальной и конечной точек пути
b
Edl .
a
b
a
Связь между напряжением, разностью потенциалов и э.д.с. следующая:
E dl Edl E
рез
a1b
или
a1b
стор
dl ,
a1b
u a1b a b e a1b .
10
8.
Если путь интегрирования представляет собой замкнутую кривую, то:u E dl E dl e .
рез
L
9
стор
L
(так как циркуляция вектора напряженности Е электростатического поля всегда
равна нулю). В контуре L сумма падений напряжения равна э. д. с. Напряжение
и э. д. с. измеряются в вольтах (В).
Рассмотрим проводящий контур а-1-b-2-а (рис. 1). На участке b-2-а
действуют сторонние силы, и на этом участке
E сторdl e .
a1b
Рис.1. Перемещение из одной точки поля в другую по
разным путям
На участке а-1-b сторонних сил нет, поэтому
u a1b a b
.
В замкнутой цепи сумма падений напряжения равна э.
д. с.
,
u a1b u b 2a e
или
a b e u b 2a .
9.
8Разность потенциалов между двумя точками рассматриваемого контура
меньше э. д. с., действующей в этом контуре.
Ток на участке а-1-b идет от точки а (точки высшего потенциала) к точке b
(точке низшего потенциала).
Если бы в цепи не было сторонних сил, то потенциалы точек а и b
выравнялись бы и ток прекратился. Наличие сторонних сил заставляет заряды
перемещаться от точки b к точке а по пути b-2-а и поддерживает потенциалы
точек а и b постоянными. Энергия стороннего поля расходуется на тепловые
потери как на участке а-1-b, так и на участке b-2-а. В тех областях проводника, в
которых имеются сторонние силы, закон Ома записывается следующим
образом:
E рез (E E стор ).
(4)
Закон Ома в дифференциальной форме справедлив как для постоянных, так
и для переменных электрических полей.
10. 2.2.3. Закон Джоуля –Ленца в дифференциальной форме.
Мощность тепловых потерь в проводнике равна произведению тока инапряжения Р = IU.
Если рассмотреть в проводящей среде элемент объема dV (рис. 2), то
мощность тепловых потерь
dP dIdU dSEdl EdV
Рис. 2. Элемент объема в проводящей среде.
2
dP
Откуда
E E 2
dV
. (5)
Формула (5) является дифференциальной
формой закона Джоуля-Ленца. Мощность
тепловых потерь в объеме V можно выразить
следующим образом:
P E 2 dV .
V
(6)
7
11. 2.2.4. Первый закон Кирхгофа в дифференциальной форме.
6Замкнутая поверхность S охватывает узел цепи, к которому подходят токи I1
и I2 и из которого выходят токи I3 и I4 (рис. 3). Согласно первому закону
Кирхгофа в интегральной форме
I1+ I2 = I 3 + I 4.
Рис. 3. Поток вектора плотности тока сквозь
замкнутую поверхность
Выразим токи через плотность тока,
считая положительную нормаль к
поверхности S направленной в наружную
сторону,
I1 dS;
I 2 dS;
I 3 dS;
I 4 dS
S1
S3
S2
S4
или
dS 0
S1 S 2 S 3 S 4
.
(7)
12.
Так как вне площадок S1, S2, S3, S4 плотность тока равна нулю, то можнораспространить интеграл на всю замкнутую поверхность S, тогда
dS 0 .
5
S
Поток вектора плотности тока сквозь замкнутую поверхность равен нулю.
Это значит, что заряд, входящий в любой объем, равен заряду, выходящему из
него за тот
же промежуток времени. Постоянный ток непрерывен. Линии
вектора замкнуты.
dS div dV .
По теореме Остроградского
S
V
Так как поверхность S, а следовательно, и объем V выбраны произвольно, то
можно считать, что
div 0.
(8)
Плотность тока проводимости не имеет источников. Формула (8) выражает в
дифференциальной форме непрерывность постоянного тока. Так как
дивергенция плотности тока проводимости равна нулю, то линии вектора
замкнуты; поэтому формулу (8) называют уравнением непрерывности для
постоянного тока.
13.
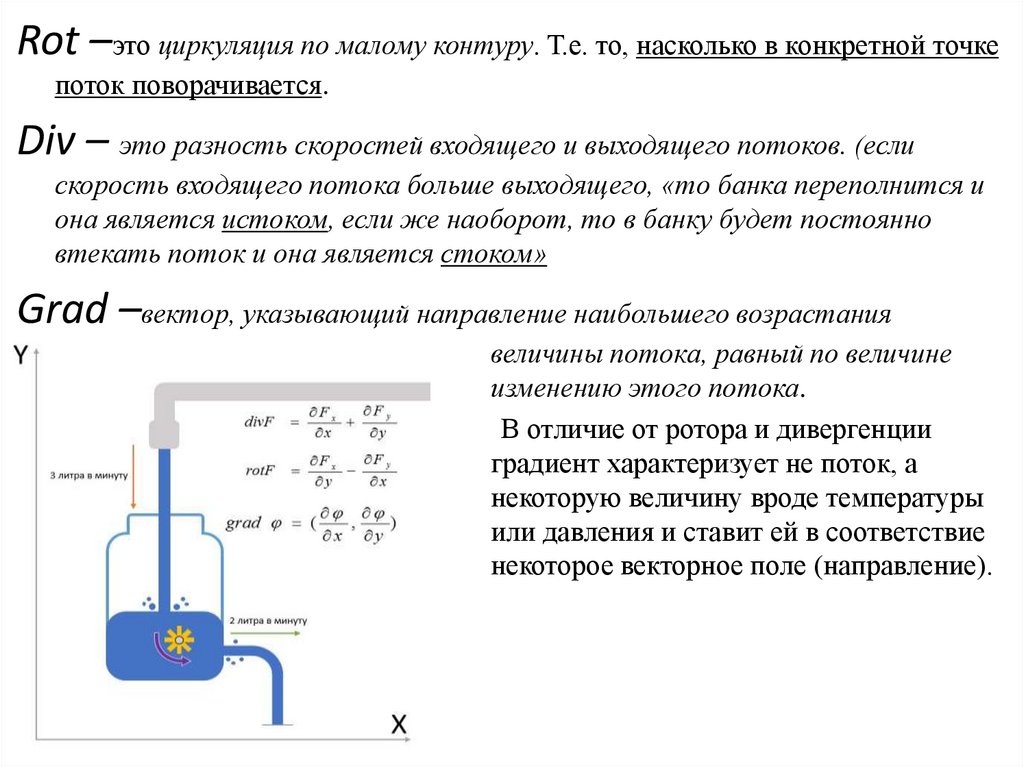
Rot –это циркуляция по малому контуру. Т.е. то, насколько в конкретной точкепоток поворачивается.
Div – это разность скоростей входящего и выходящего потоков. (если
скорость входящего потока больше выходящего, «то банка переполнится и
она является истоком, если же наоборот, то в банку будет постоянно
втекать поток и она является стоком»
Grad –вектор, указывающий направление наибольшего возрастания
величины потока, равный по величине
изменению этого потока.
В отличие от ротора и дивергенции
градиент характеризует не поток, а
некоторую величину вроде температуры
или давления и ставит ей в соответствие
некоторое векторное поле (направление).
14.
4Постоянный ток имеет в различных сечениях неразветвленной цепи одно и
то же значение, так как в противном случае были бы такие участки, в которых
заряд или увеличивается, или уменьшается, а это невозможно.
Отметим, что дивергенция плотности переменного тока может быть отлична
от нуля, так как в цепях переменного тока могут быть участки, на которых
заряды увеличиваются или уменьшаются (конденсатор в цепи переменного
тока).
15. 2.2.5. Граничные условия.
32.2.5. Граничные условия.
Рассмотрим границу двух проводящих сред, проводимости которых равны
1 и 2. Построим цилиндрическую поверхность S так, как показано на рис. 4.
Так как ток равен потоку вектора
плотности тока, то:
dS 0 1dS 2dS dS .
S
S1
S2
Sбок
Если высоту цилиндра уменьшить так, чтобы
площадки S1 = S2 совпали с граничной
поверхностью, и учитывая, что для небольших S
вектор можно считать одинаковым во всех точках этих
площадок, получим:
1n S 2n S 0
Ток сквозь боковую поверхность при этом станет
равным нулю. Сокращая на S, получим граничное
условие
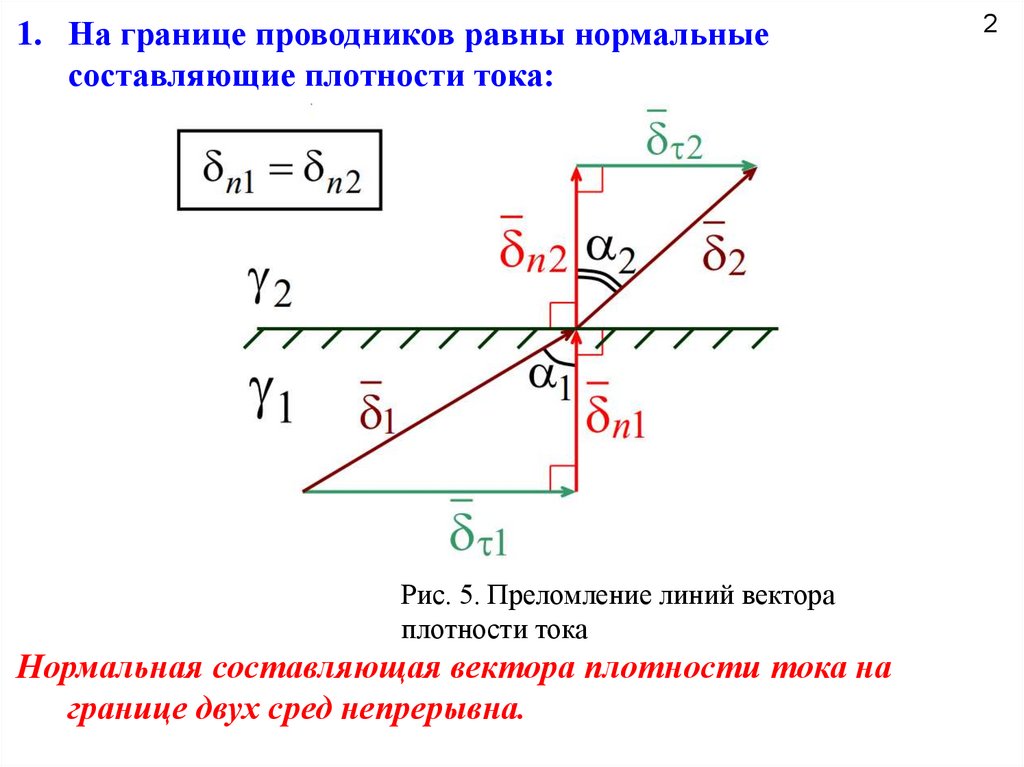
1n 2n .
Рис.4. Граничные условия для
вектора плотности тока
16.
1. На границе проводников равны нормальныесоставляющие плотности тока:
Рис. 5. Преломление линий вектора
плотности тока
Нормальная составляющая вектора плотности тока на
границе двух сред непрерывна.
2
17.
2Рис.4. Граничные условия для
вектора плотности тока
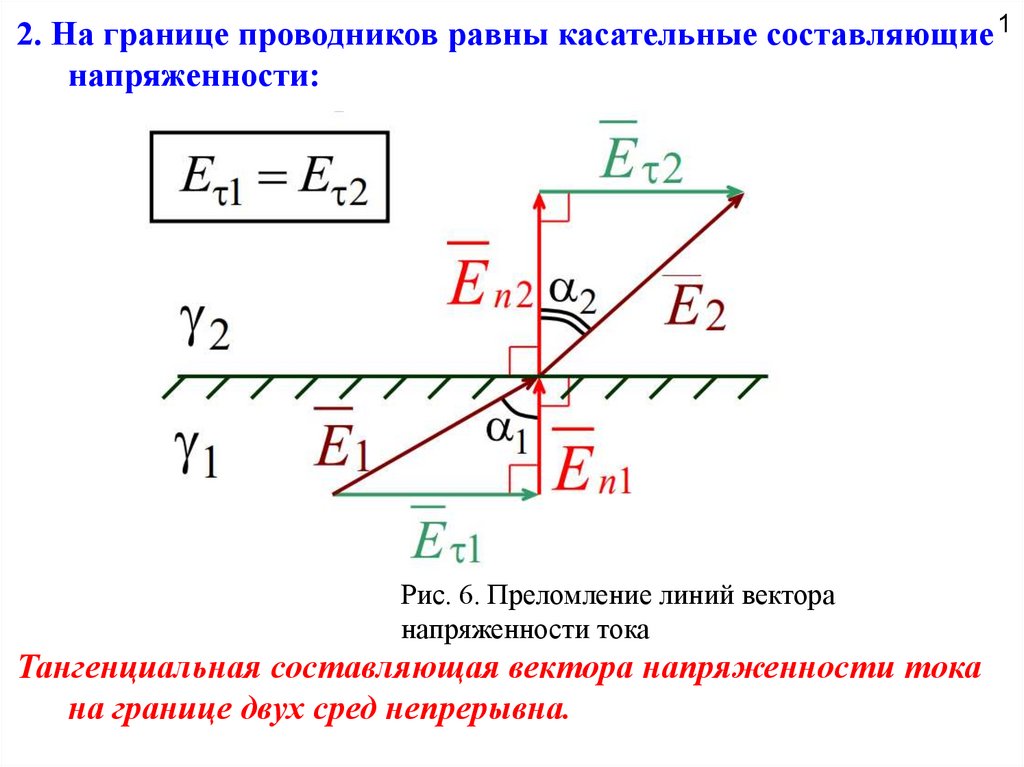
Если на границе этих сред нет сторонних сил, то касательные
(тангенциальные) составляющие вектора напряженности электрического поля
также должны быть непрерывны у границы E1 E 2 .
18.
2. На границе проводников равны касательные составляющие 1напряженности:
Рис. 6. Преломление линий вектора
напряженности тока
Тангенциальная составляющая вектора напряженности тока
на границе двух сред непрерывна.
19.
0Если векторы и Е образуют с нормалью к границе угол 1 в первой среде и
угол 2 — во второй среде (рис. 5 и 6), то
Так как 1= 1E1; 2= 2E2, то
E1sin 1= E2sin 2;
1cos 1= 2cos 2.
1 tg 1
2 tg 2
.
Следовательно удельная проводимость испытывает скачек
на границе двух проводников.
20.
Задача 1. На границе раздела двух проводников с удельнымипроводимостями γ1 и γ2 заданы модули векторов плотности тока δ1=20 (А/мм2
); δ2=30,41 (А/мм2 ) и угол α1=30°. Определить для удельных проводимостей
отношение γ2 /γ1
Решение. Из равенства нормальных составляющих плотностей тока на
границе раздела двух проводников δ1 cos(α1 ) =δ2cos(α2) находим угол выхода
вектора плотности тока в проводнике с γ2 :
Далее из уравнения
определяем искомое отношение:
21.
Задача 2. На границе раздела двух проводников с удельнымипроводимостями γ1=3γ0 и γ2 =γ0 заданы модуль вектора напряженности
Е1=11,547 (В/м) и угол α1=60°. Определить модуль вектора напряженности Е2
(В/м) в проводнике с удельной проводимостью γ2 =γ0 .
Решение. Из уравнения (1) находим угол выхода вектора напряженности в
проводнике с γ2 :
Далее из равенства касательных составляющих напряженностей Esin( 1) =E
sin( 2) определяем искомый модуль вектора напряженности:
22. заключение
Т. о., в результате рассмотрения материала вы получили знания о:- токе и плотности тока проводимости;
- законе Ома в дифференциальной форме;
- законе Джоуля –Ленца в дифференциальной форме;
- первом законе Кирхгофа в дифференциальной форме;
- граничных условиях.



















 physics
physics








