лк2

1.

Тема 2
Основные законы теории
электромагнитного поля
Лекции № 1
1. Система уравнений электродинамики.
1

2.

Вопросы:
1.
Введение. Основные понятия
электродинамики.
2.
Уравнения Максвелла в интегральной и
дифференциальной формах.
2

3.

1 Введение. Основные понятия электродинамики
Электродинамика – наука, описывающая
поведение электромагнитного поля,
осуществляющего взаимодействие между
зарядами.
Электромагнитное поле - особый вид материи,
оказывающий на заряженные частицы силовое
воздействие, зависящее от скорости и заряда
частиц, определяемый во всех точках двумя
векторными величинами, которые характеризуют
две его стороны, называемые соответственно
электрическим полем и магнитным полем.
3

4.

Классическая электродинамика - макроскопическая.
Это определяется оперированием со значениями
электромагнитных величин, усредненными по времени и
пространству.
Усреднение производится для интервалов времени,
значительно больших периодов обращения или
колебания элементарных заряженных частиц в атомах
или молекулах, а также для участков поля, объемы
которых во много раз превышают объемы атомов и
молекул.
4

5.

История развития электродинамики
Простейшие электрические и магнитные явления были
известны еще в древние времена.
1600г. англичанин У.Гильберт разграничил данные явления.
17 – первая половина 18 вв. - многочисленные опыты с
наэлектризованными телами.
Вторая половина 18 века
- начало количественного
изучения электрических явлений:
- появление измерительных приборов (электроскопы
различных конструкций);
- экспериментальное установление основного закона
электростатики
(взаимодействие
неподвижных
точечных электрических зарядов; англичанин
- Г. Кавендиш и француз Ш. Кулон).
5

6.

19 век
- экспериментальное и теоретическое
исследование:
- 1820г.
- выявление связи между электрическими и
магнитными явлениями (датчанин Ч.Эрстед);
- 1826г. – выявление количественной зависимости
электрического тока от напряжения (немец Г.Ом);
- 1830г. – основная теорема электростатики (теорема
Гаусса);
- 1830-1840гг. – развитие ЭД англичанином М. Фарадеем
(электрические и магнитные явления рассматриваются с
единой точки зрения);
- 1861-1873гг. – теоретические исследования и обобщения
Дж.
Максвеллом
(Англия)
формулировка
фундаментальных уравнений электродинамики;
- 1886-1889гг.
– экспериментальное подтверждение
теории Максвелла – работы Г.Герца;
- 1896г. – создание радио А.С. Поповым.
6

7.

Основные понятия электродинамики
Одно из проявлений существования ЭМП – воздействие поля с
силой Лоренца F на движущийся со скоростью v
электрический заряд Q:
F ( p, t ) Q( E ( p, t ) [v, B( p, t )])
(1.1)
где E ( p, t ) - вектор напряженности электрического поля;
B( p, t ) - вектор магнитной индукции;
t – время.
7

8.

Основные понятия электродинамики
Векторы
Электрическое поле
Магнитное поле
напряженности
E
[В/м]
H
[А/м]
индукции
D
[Кл/м]
B
[Тл]
Материальные
уравнения:
D a E
B a H
a 0 , a 0 - абсолютные диэлектрическая и магнитная
проницаемости среды соответственно;
0 10 9 /(36 ) [Ф/м] – электрическая постоянная;
0 4 10 7
[Гн/м] – магнитная постоянная;
, относительные
диэлектрическая
и
магнитная
проницаемости.
Объемная плотность электрического заряда: lim q
V 0 V
8

9.

Основные понятия электродинамики
Объемная плотность электрического заряда:
q
lim
V 0 V
Векторное поле объемной плотности тока проводимости:
I
j lim i0
S 0
S
э
где q - заряд, содержащийся в объеме V ;
S - площадка, ориентированная перпендикулярно движению
зарядов;
i0 - орт нормали, указывающий направление движения;
I - ток, проходящий через S .
Предельные переходы здесь следует понимать как условные (должны
содержать достаточно большое число элементарных частиц).
Закон Ома в дифференциальной форме:
- удельная проводимость вещества.
j E
9

10.

2. Уравнения Максвелла в
интегральной и
дифференциальной формах.
10

11.

Уравнения, сформулированные Джеймсом
Клерком Максвеллом, возникли на основе
ряда важных экспериментальных открытий,
которые были сделаны в начале XIX века.
В частности, были известны:
закон Кулона, описывающий силу взаимодействия между
электрическими зарядами, теорема Гаусса,
закон
БиоСавара,
описывающий
магнитные
поля,
возбуждаемые движущимися электрическими зарядами и
закон Ампера,
Сила Лоренца - сила, с которой, в рамках классической
физики, электромагнитное поле действует на точечную
заряженную частицу.
законы электромагнитной индукции Фарадея, согласно
которым изменение магнитного потока порождает
электрическое поле и индуцирует ток в проводниках (см.
также Правило Ленца).
гипотеза об отсутствии в природе магнитных монополей.
11

12.

Теория Максвелла
Анализируя связь между величинами электрического
и магнитного поля и обобщая результаты опытов Эрстеда и
Фарадея, Максвелл создал теорию электромагнитного
поля. Теория Максвелла – теория близкодействия, согласно
которой электрические и магнитные взаимодействия
распространяются со скоростью, равной скорости света в
данной среде.
В основе теории Максвелла лежат два положения.
1. Всякое переменное электрическое поле порождает
вихревое магнитное поле.
2. Всякое переменное магнитное поле порождает
вихревое электрическое поле
12

13.

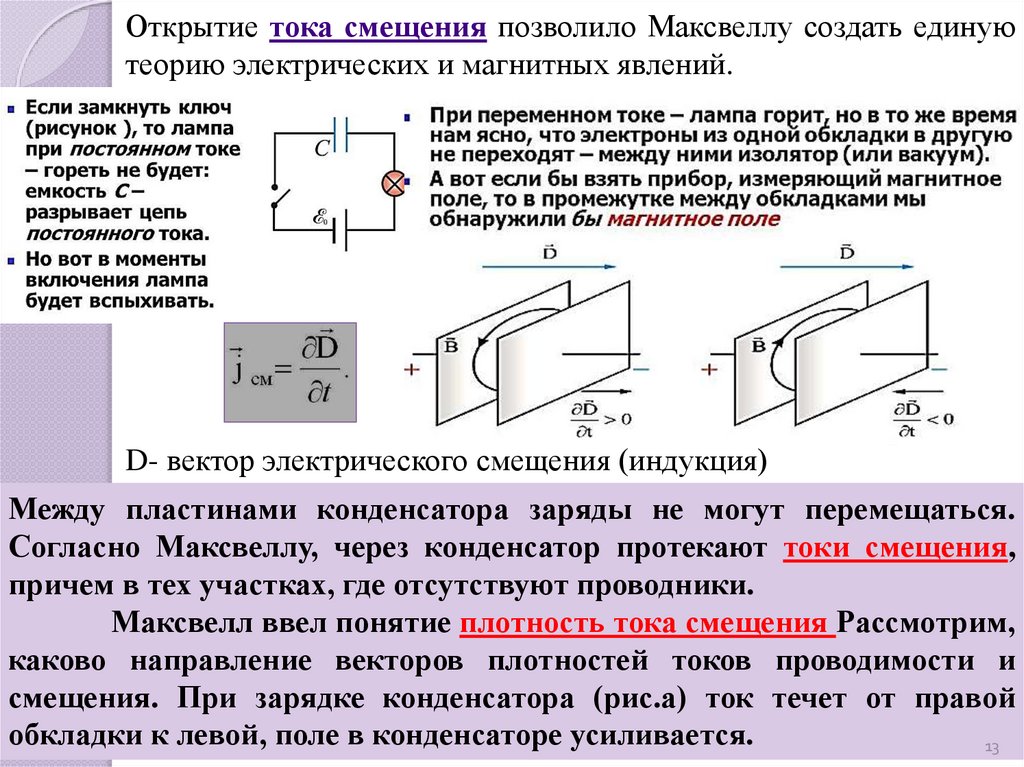
Открытие тока смещения позволило Максвеллу создать единую
теорию электрических и магнитных явлений.
D- вектор электрического смещения (индукция)
Между пластинами конденсатора заряды не могут перемещаться.
Согласно Максвеллу, через конденсатор протекают токи смещения,
причем в тех участках, где отсутствуют проводники.
Максвелл ввел понятие плотность тока смещения Рассмотрим,
каково направление векторов плотностей токов проводимости и
смещения. При зарядке конденсатора (рис.а) ток течет от правой
обкладки к левой, поле в конденсаторе усиливается.
13

14.

В природе можно выделить два вида токов:
ток связанных зарядов и ток проводимости.
это
перемещение
средних
положений
связанных электронов и
ядер,
составляющих
молекулу, относительно
центра молекулы
это направленное движение на
большие расстояния свободных
зарядов (например, ионов или
свободных электронов).
В случае, если этот ток идёт не в
веществе,
а
в
свободном
пространстве,
нередко
вместо
термина
«ток проводимости» употребляют
термин «ток переноса». Иначе
говоря, ток переноса обусловлен
переносом электрических зарядов в
свободном
пространстве
заряженными частицами или телами
под действием электрического поля.
14

15.

В общем случае, токи проводимости и смещения в
пространстве не разделены, они находятся в одном и том же
объеме. Поэтому Максвелл ввёл понятие полного тока
Закон показывает, что причиной возникновения магнитного
поля является в равной степени и ток переноса, и ток
смещения, а также устанавливает количественную связь между
током и магнитным полем.
Ток смещения называется током, потому что его
действие такое же, как тока переноса. Физически ток смещения
обнаруживается потому, что переменное электрическое поле
вызывает появление магнитного поля.
15

16.

В среде движутся электрические заряды
образуя
конвекционный ток, плотность тока jk.
Электрический ток вызывает магнитное поле Н.
Выделим в пространстве контур L на который опирается
поверхность S. Величина тока который пронизывает эту
поверхность равна интегралу плотности тока по поверхность S,
количественную
связь
между
величиной
тока
и
напряженностью магнитного поля установил АМПЕР,
опытным путем он установил ток
пронизывающий поверхность S
равен
циркуляции
вектора
напряженности магнитного поля по
контуру L. Чтобы вычислить
циркуляцию надо в каждой точки
контура вектор напряженности поля
скалярно умножить на векторный
элемент дуги dl и проинтегрировать
по контуру.
16

17.

Будем заряжать плоский конденсатор от
электрической батареи
Рассмотрим
состояние
системы
в
некоторый момент времени
Построим поверхность S опирающийся
на контур L.
если уменьшать контур L стягивая в
точку , циркуляция вектора магнитного
поля будет стремиться к нулю, между
тем амперметр в цепи конденсатора
показывает , что ток втекает внутрь
поверхность
s
,таким
образом
интегралы не равны друг другу
17

18.

Как разрешить эти противоречия, предположим что через
поверхность S наружу вытекает такой же ток какой втекает во
внутрь тогда сумма токов будет равна нулю Максвелл назвал это
ток смещения. Ток смещения связан с изменением во времени
электрического поля и плотность его равна скорости изменения
вектора электрической индукции D.
Мы получили закон полного тока (первое
уравнение
электродинамики)
в
интегральной форме.
Согласно этому закону, циркуляция вектора напряженности
магнитного поля по замкнутому контуру равна полному току,
протекающему сквозь поверхность, натянутую на этот контур 18

19.

Первое уравнение электродинамики: закон полного тока
(Закон Ампера).
Закон полного тока в дифференциальной форме ( для решения
задач:
э
D
ro tH j
t
Согласно этому закону, вихрь вектора напряженности
магнитного поля в каждой точке равен объемной плотности
полного тока в этой точке.
Для получения закона полного тока в интегральной форме
проинтегрируем уравнение по произвольной поверхности S
rot HdS Hdl ,
S
Используя теорему Стокса о
связи между интегралами по
контуру и по поверхности
l
19

20.

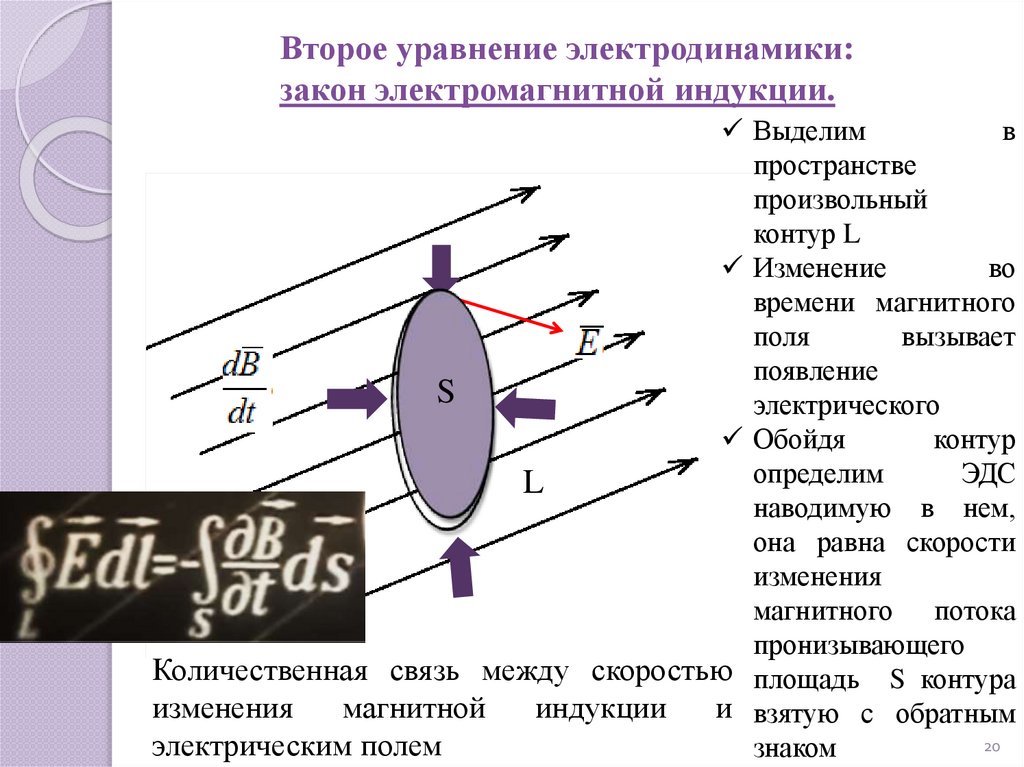
Второе уравнение электродинамики:
закон электромагнитной индукции.
Выделим
в
пространстве
произвольный
контур L
Изменение
во
времени магнитного
поля
вызывает
появление
S
электрического
Обойдя
контур
определим
ЭДС
L
наводимую в нем,
она равна скорости
изменения
магнитного потока
пронизывающего
Количественная связь между скоростью площадь S контура
изменения
магнитной
индукции
и взятую с обратным
20
электрическим полем
знаком

21.

Второе уравнение электродинамики:
закон электромагнитной индукции.
Закон электромагнитной индукции в интегральной форме
магнитный поток
(поток
вектора
магнитной
индукции) через
поверхность S.
Согласно этому закону, меняющееся во времени магнитное
поле вызывает независимо от параметров среды такое
электрическое поле, что для всякого произвольного контура
циркуляция вектора напряженности этого поля равна взятой с
обратным знаком скорости увеличения магнитного потока через
поверхность, ограниченную этим контуром.
21

22.

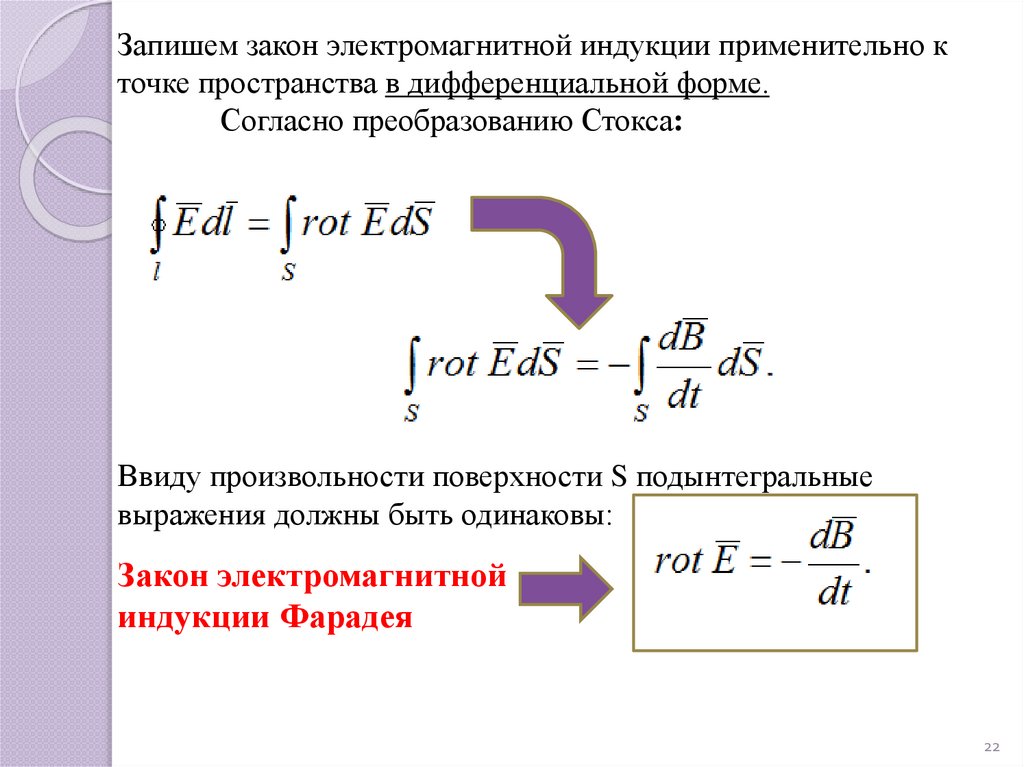
Запишем закон электромагнитной индукции применительно к
точке пространства в дифференциальной форме.
Согласно преобразованию Стокса:
Ввиду произвольности поверхности S подынтегральные
выражения должны быть одинаковы:
Закон электромагнитной
индукции Фарадея
22

23.

Третье уравнение электродинамики: закон
непрерывности магнитного поля.
B dS 0
S
В магнитной поле
выделим объем V ,
линии магнитного
поля
замкнуты,
сколько их входит в
объем столько же
выходит
наружу,
следовательно
поток вектора Вഥ по
замкнутой
поверхности равен
нулю
МАГНИТНЫЕ ЗАРЯДЫ В ПРИРОДЕ НЕ СУЩЕСТВУЮТ И
СИЛОВЫЕ ЛИНИИ МАГНИТНОГО ПОЛЯ ЗАМКНУТЫ САМИ
23
НА СЕБЯ

24.

Третье уравнение электродинамики: закон
непрерывности магнитного поля.
Закон непрерывности магнитного поля в интегральной форме:
Согласно этому закону, магнитный поток сквозь замкнутую
поверхность равен нулю. Для того чтобы получить этот закон в
дифференциальной
форме,
используем
преобразование
Остроградского-Гаусса
Так как объем V произволен, то
подынтегральное
выражение
равно нулю
24

25.

Мы получили закон (уравнение) непрерывности магнитного поля
в дифференциальной форме. Он показывает, что магнитное поле
не имеет истоков. Линии индукции магнитного поля всегда
замкнутые.
Закон непрерывности справедлив для любых полей в любой
среде, потому что в любой среде индукции поля учитывают и
внешнее, и наведенное поле.
25

26.

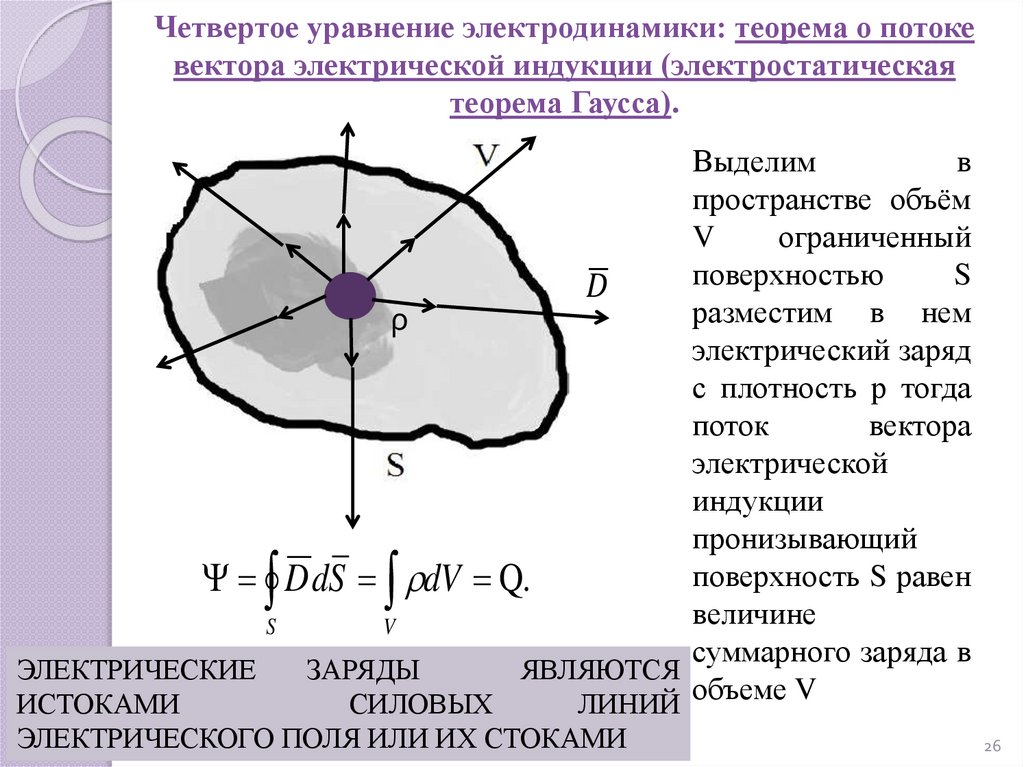
Четвертое уравнение электродинамики: теорема о потоке
вектора электрической индукции (электростатическая
теорема Гаусса).
Выделим
в
пространстве объём
V
ограниченный
поверхностью
S
ഥ