Similar presentations:
Чертежи и развертки простых геометрических тел
1. «Чертежи и развертки простых геометрических тел»
«Чертежи и развертки простыхгеометрических тел»
Путь от идей до воплощенья долог,
Извилист, полон терний, и тяжел.
И здесь конструктор - главный идеолог
С рабочим инструментом - чертежом.
Чертёж, идей и мыслей переводчик,
Первоначально нужен нам затем,
Чтоб поняли технолог и расчётчик
Всю логику моделей, схем, систем.
Да и рабочих целая бригада Все знают, не великий здесь секрет Без чертежа не сделает как надо
Ракету, самолет и табурет.
2.
3.
Классификация геометрическихобъектов
Линии
4.
Классификация геометрическихобъектов
Линии
Плоские фигуры
5.
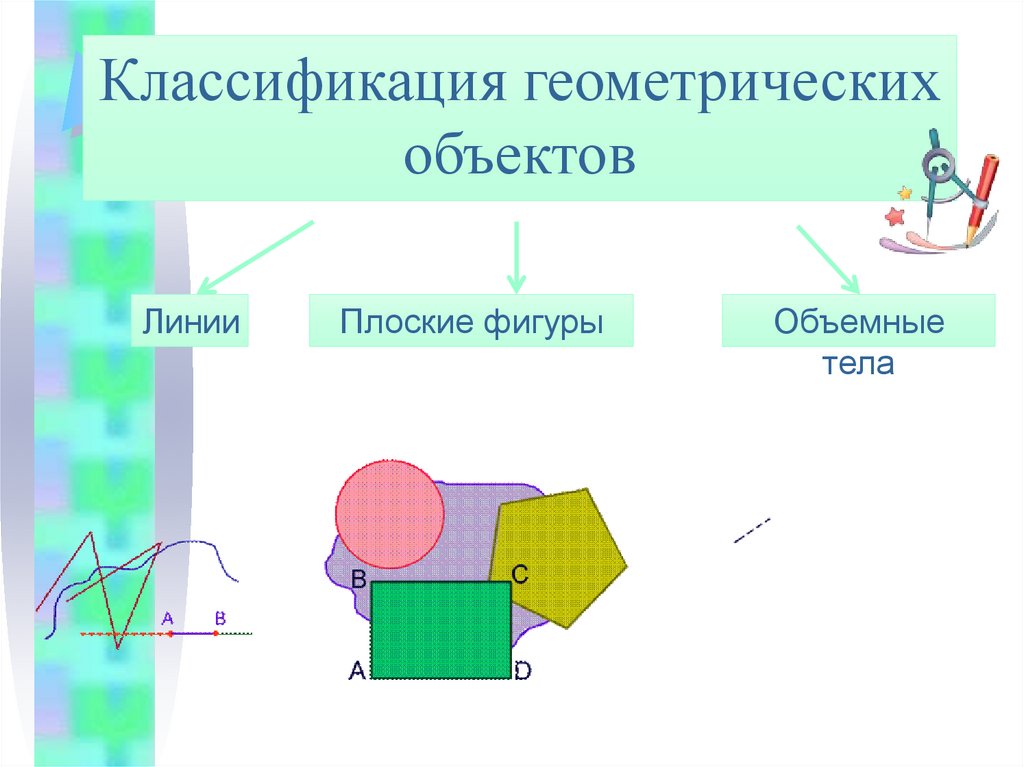
Классификация геометрическихобъектов
Линии
Плоские фигуры
Объемные
тела
6.
ЛинииКривая
Ломаная
Прямая
7.
Плоские фигурыКруг
Многоугольники
Овал
Четырехугольник
Треугольники
n-угольники
8.
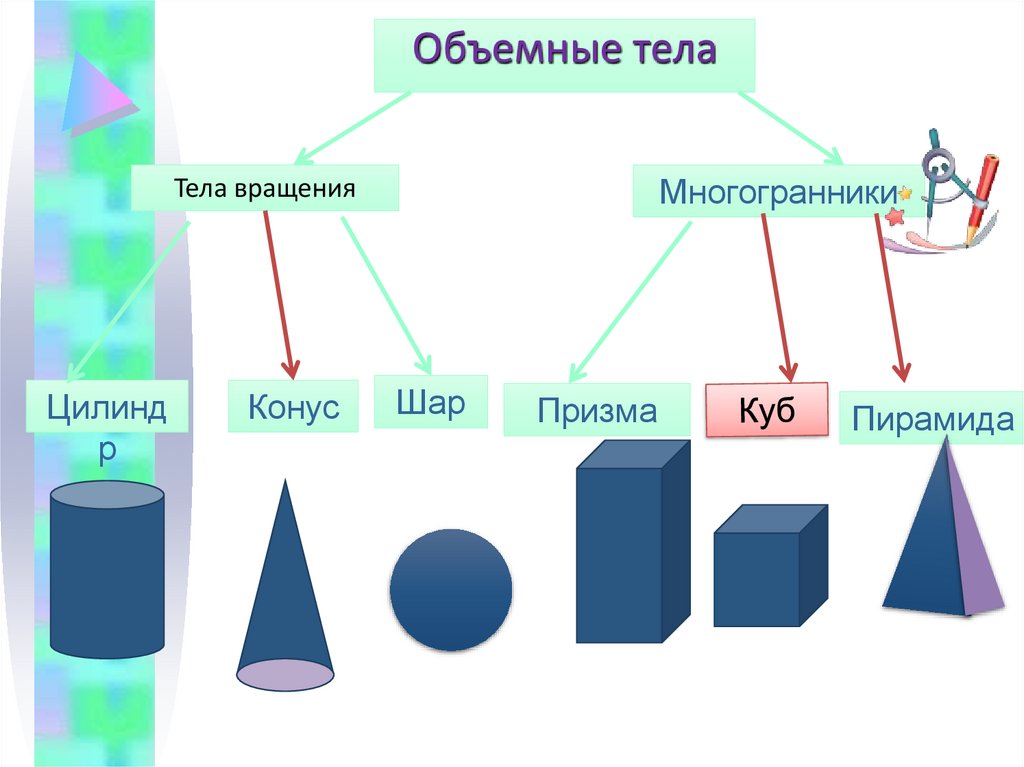
Объемные телаМногогранники
Тела вращения
Цилинд
р
Конус
Шар
Призма
Пирамида
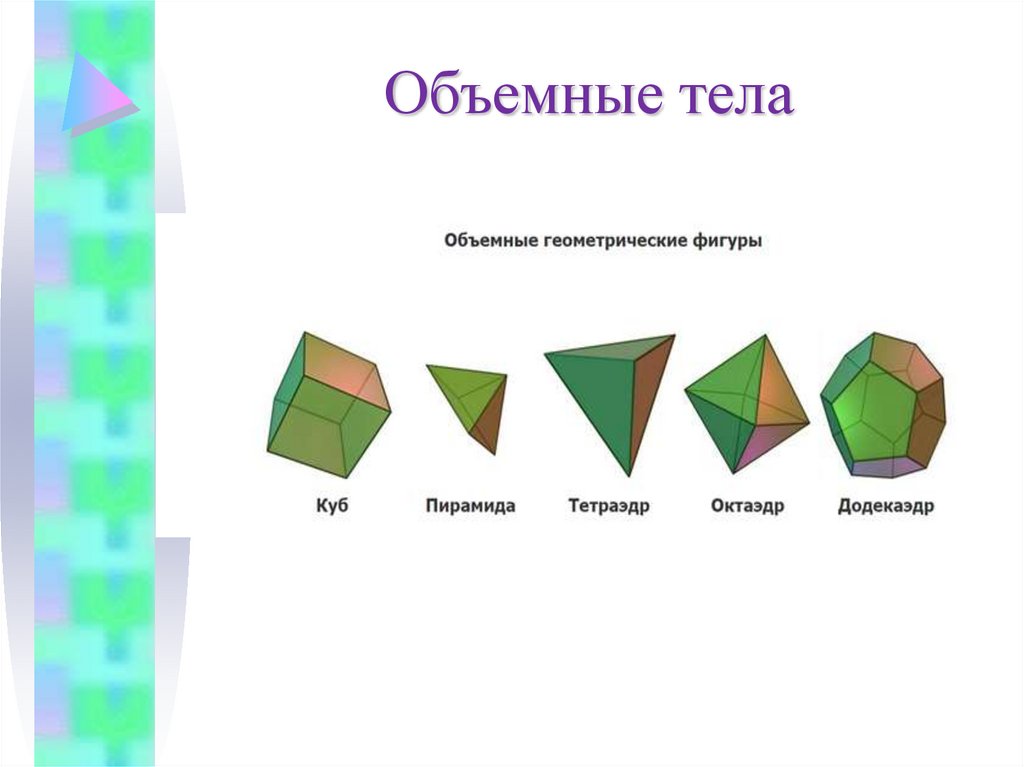
9. Объемные тела
10. Объемные тела
• Моделирование из бумаги макетовгеометрических тел
11. РАЗВЕРТКА
• С развёртками поверхностей мы частовстречаемся в обыденной жизни, на
производстве, в строительстве. Чтобы
изготовить упаковку для сока, конфет,
духов, праздничную коробочку или
кулёк и т.п., надо уметь строить
развёртки поверхностей
геометрических тел.
12. РАЗВЕРТКА
• «Развёртка» - представляет собойплоский многоугольник, состоящий из
меньших многоугольников – граней
исходного многогранника.
13. Изготовление развертки
• Изготовить объемное тело при помощиразвертки можно, вычертив
необходимое количество фигур,
соединённых между собой линиями
сгиба (штрихпунктирная с двумя
точками) и равных сторонами (гранями)
этого объемного тела
14. Инструменты и материалы, необходимые для выполнения макетов геометрических тел
15. Развертка КУБА
Для построения развертки куба достаточно знать размер ребра
куба. Допустим размер ребра куба = 70 мм.
Берем в руки линейку и карандаш. (Помним правила техники
безопасности при работе с чертежными инструментами,
ножницами).
Чертим в середине листа картона квадрат со сторонами 70 мм.
Сколько у куба граней? Правильно – 6. Достраиваем развертку.
Вырезаем, склеиваем.
16.
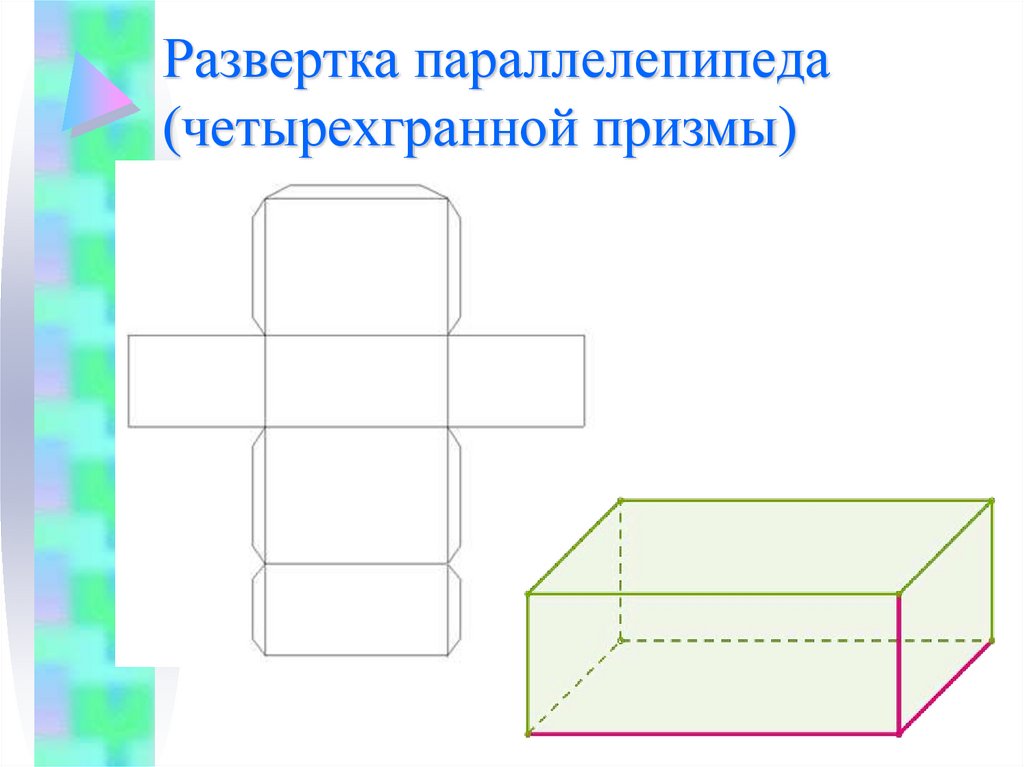
17. Развертка параллелепипеда (четырехгранной призмы)
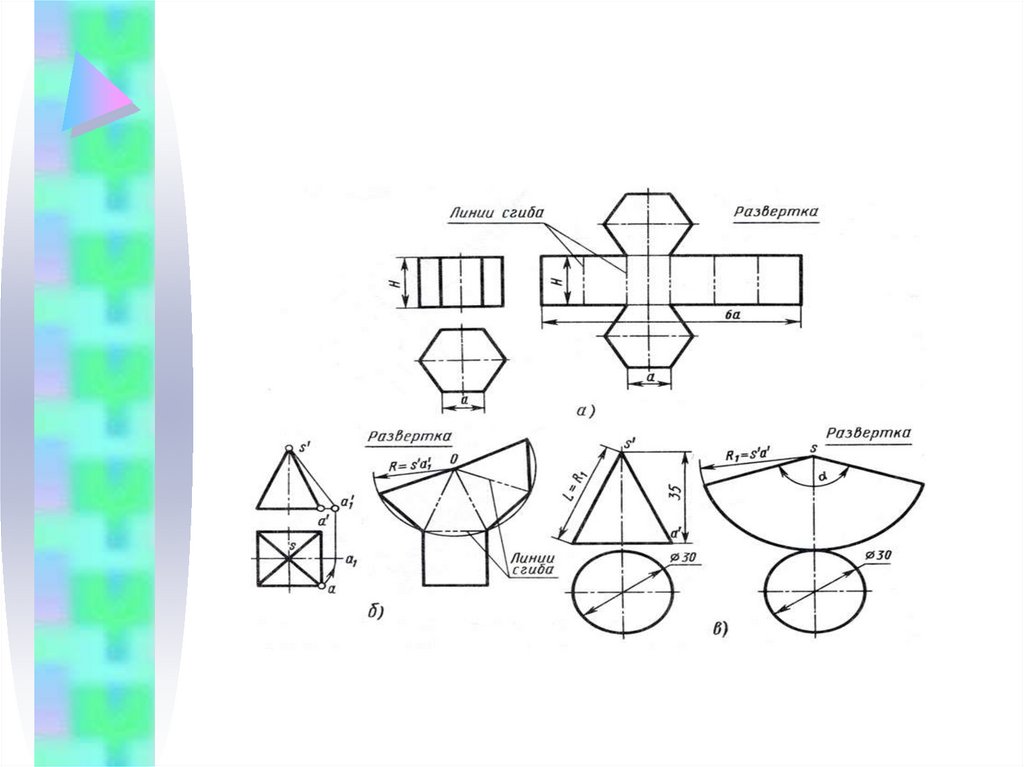
18. Развертка ПИРАМИДЫ
Для того чтобы выполнить развёртку, давайте определим из каких
фигур состоит пирамида.
Боковая поверхность пирамиды состоит из четырех равных
треугольников. Для построения треугольника необходимо знать
величины его сторон. Равные ребра пирамиды служат боковыми
сторонами граней (треугольниками). Из произвольной точки
описываем дугу радиусом, равным длине бокового ребра пирамиды. На этой дуге откладываем четыре отрезка, равные
стороне основания. Крайние точки соединяем прямыми с центром
описанной дуги. Затем пристраиваем квадрат, равный основанию
пирамиды.
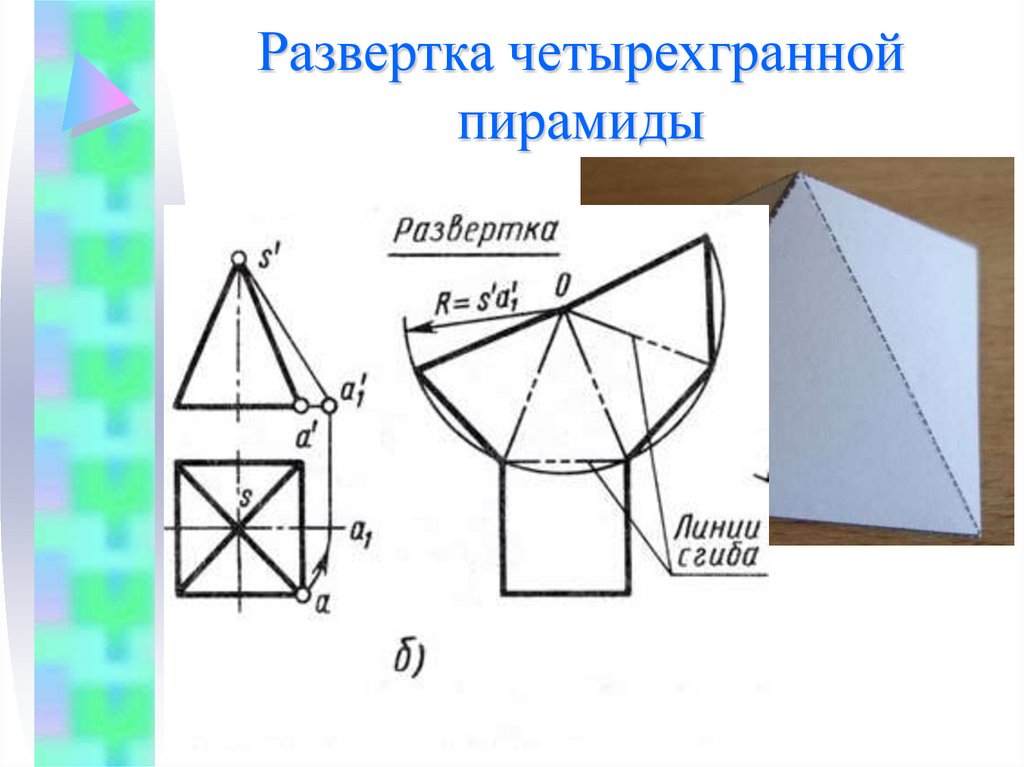
19. Развертка четырехгранной пирамиды
20. Развертка шестигранной пирамиды
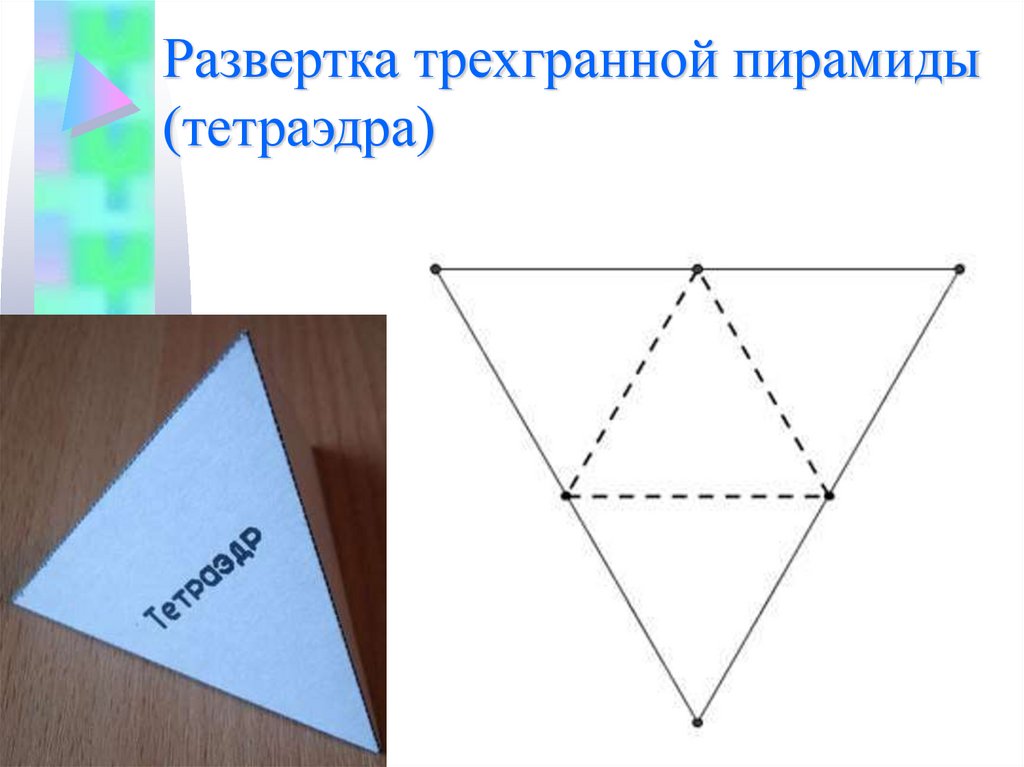
21. Развертка трехгранной пирамиды (тетраэдра)
22.
23.
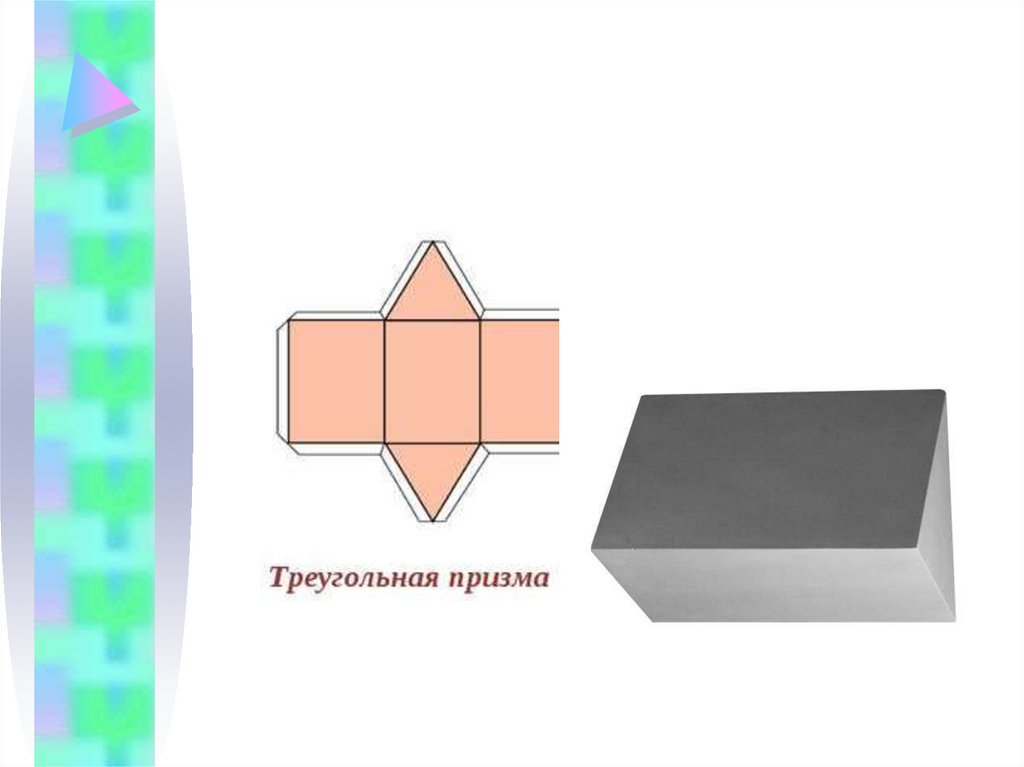
24. Развертка трехгранной призмы
25.
26. Развертка шестигранной призмы
27. Развертка пятигранной призмы
28.
29. Развертка цилиндра
Развёртка боковой поверхности цилиндра состоит из прямоугольника и двухкругов. Одна сторона прямоугольника равна высоте цилиндра, другая –
длине окружности основания.
Длина окружности высчитывается по формуле: L= Пи*D.
На чертеже развёртки к прямоугольнику пристраивают два круга, диаметр
которых равен диаметру основания цилиндра.
30. Развертка цилиндра
31.
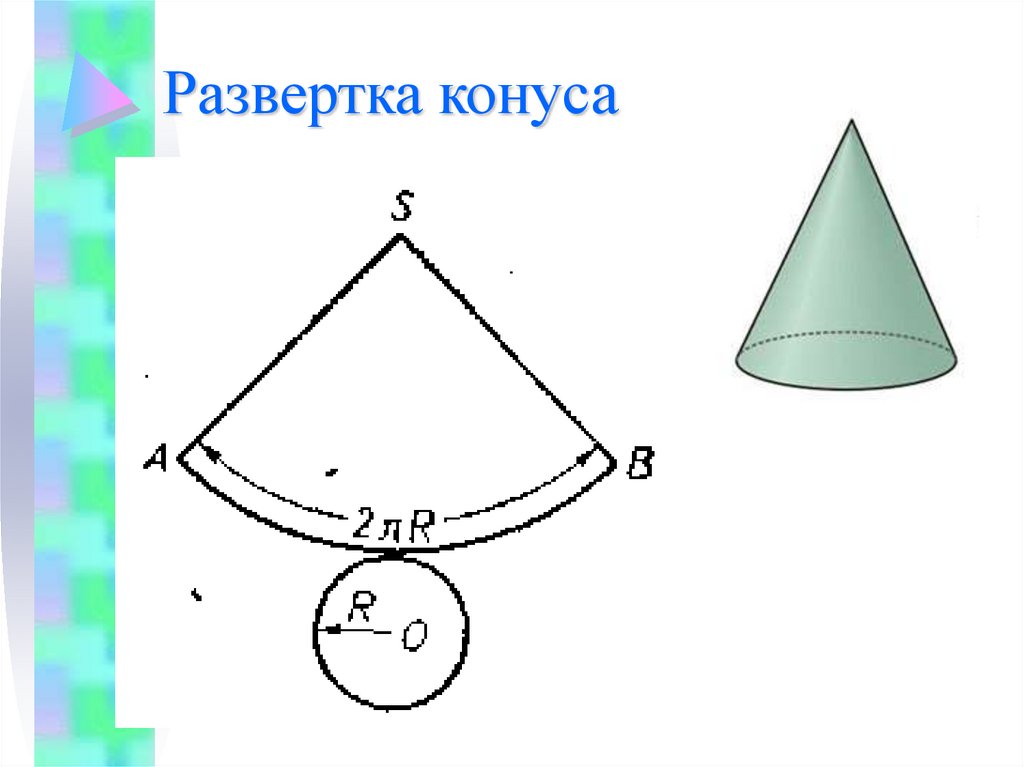
32. Развертка конуса
33. Развертка конуса
34.
35. Развертка додекаэдра
36.
37.
38.
39.
40.
41.
42. Домашнее задание
• Изготовить модельгеометрического тела высотой не
менее 20 см

































 mathematics
mathematics








