Similar presentations:
Теория вероятностей. Математическая статистика
1.
математическая статистика2.
Статистическое исследованиеСтатистическая совокупность
Статистическая закономерность
Признак
Статистический ряд
3.
Математическая статистикаМатематическая статистика – наука, изучающая
методы сбора, сокращения, анализа и интерпретации
статистических данных, относящихся к случайным
явлениям
Статистика исследует массовые явления и процессы,
выступающие как множество отдельных факторов,
обладающих как индивидуальными, так и общими
признаками
4.
Функции статистикиИнформационная – сбор, обобщение и представление
информации
Прогностическая – оценивание вероятностей тех или
иных случайных событий
Аналитическая – количественное исследование
тенденций процесса, изучение процесса в динамике,
измерение связей между факторами, влияющими на
процесс
5.
Основные понятияматематической статистики
Объект
статистического
исследования
–
статистическая совокупность
Статистическая совокупность – множество единиц,
обладающих
массовостью,
однородностью,
определенной целостностью, взаимозависимостью
состояния отдельных единиц и наличием вариации
Каждая
единица
обладает
некоторым
набором
признаков
Признаки
могут быть общими
совокупности и индивидуальными
у
всех
единиц
6.
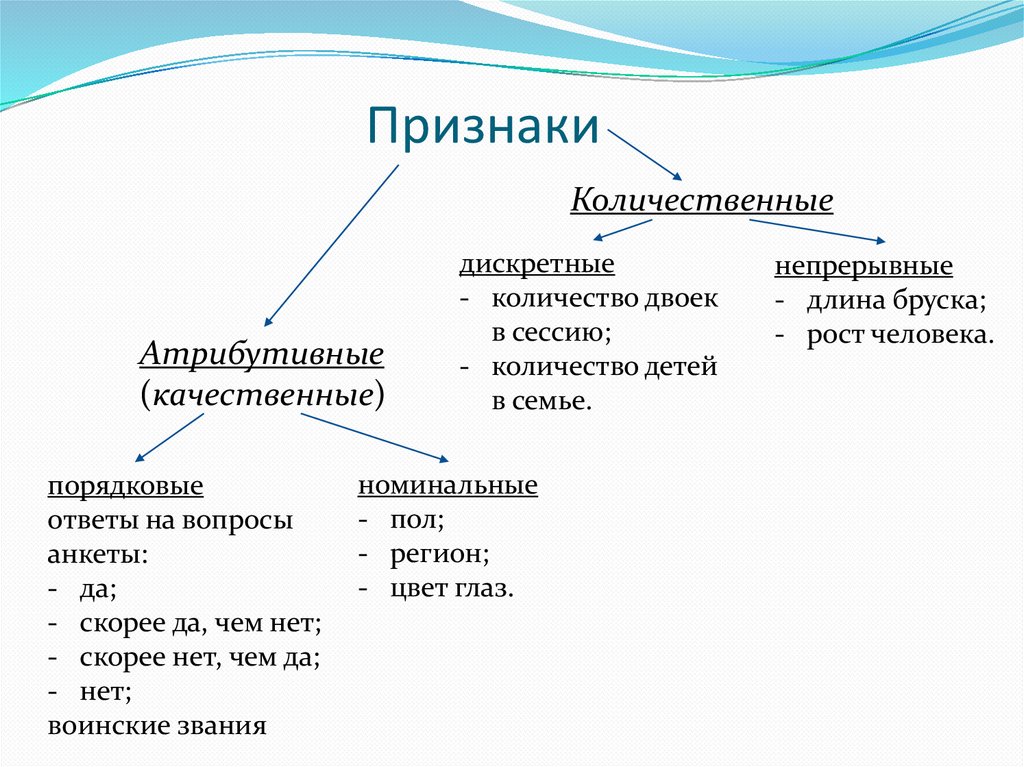
ПризнакиКоличественные
Атрибутивные
(качественные)
порядковые
ответы на вопросы
анкеты:
- да;
- скорее да, чем нет;
- скорее нет, чем да;
- нет;
воинские звания
дискретные
- количество двоек
в сессию;
- количество детей
в семье.
номинальные
- пол;
- регион;
- цвет глаз.
непрерывные
- длина бруска;
- рост человека.
7.
Статистические рядыВариационные
Атрибутивные
по атрибутивному
признаку
дискретные
Интервальные
по дискретному по непрерывному
признаку
признаку или
по дикретному
с большим числом
вариант
8.
Статистические рядыВарианта – отдельное значение признака, которое он
принимает в вариационном ряду
Частота – численность каждой группы
вариационного ряда
Частость – частота, выраженная в долях единицы или
в процентах к итогу
9.
Статистические рядыЧисло детей в
семье, чел.
Удельный вес, %
Число семей, ед.
к итогу
1
600
60,0
2
300
30,0
3
100
10,0
Итого
1000
100
10.
Статистическое исследованиеЗадача статистики – выявление статистических
закономерностей на основе анализа массовых данных
Этапы статистического исследования:
статистическое наблюдение (сбор и регистрация
данных);
сводка и группировка результатов наблюдения
(предварительная обработка полученных данных);
анализ полученных показателей.
11.
12.
СводкаСводка – это комплекс последовательных операций по
обобщению конкретных единичных фактов,
образующих совокупность, для выявления типичных
черт и закономерностей, присущих изучаемому
явлению в целом.
Простая сводка — это операция по подсчету общих
итогов по совокупности единиц наблюдения.
Сложная сводка — это комплекс операций,
включающих группировку единиц наблюдения,
подсчет итогов по каждой группе и по всему объекту
и представление результатов группировки и сводки в
виде статистических таблиц.
13.
Сводка и группировкаЭтапы сложной сводки:
выбор группировочного признака;
определение порядка формирования групп;
разработка системы статистических показателей для
характеристики групп и объекта в целом;
разработка макетов статистических таблиц для
представления результатов сводки.
Группировкой называется разделение единиц
изучаемой совокупности на однородные группы по
определенным, существенным для них признакам.
14.
Число интервалов группировкиФормула Стерджесса
k 1 log n 1 3,322 lg n
2
n , n 100
k
(2 4) lg n, n 100
Величина интервала
R x x
h
k
k
max
min
15.
Виды группировокТипологическая – разделение качественно
неоднородной совокупности на отдельные качественно
однородные группы и выявление на этой основе
различных типов явлений
Структурная – выявление закономерностей
распределения единиц однородной совокупности по
варьирующим значениям исследуемого признака
Аналитическая – исследование взаимосвязей
варьирующих признаков (двух или более) в пределах
однородной совокупности
16.
ПримерИмеются данные об успеваемости 30 студентов по
некоторому предмету: 5, 4, 3, 3, 5, 4, 4, 4, 3, 4, 4, 5, 4, 4, 3,
2, 5, 3, 4, 4, 4, 3, 2, 5, 2, 5, 5, 2, 3, 3.
Построить
типологическую группировку, взяв за
группировочный признак успеваемость студента
(успевает [3 и выше]/не успевает [2]);
структурную группировку по оценкам, полученным в
сессию.
17.
ПримерУспевающих
Не успевающих
26
4
Оценка
2
3
4
5
Количество
человек
4
8
11
7
18.
ПримерИзвестны следующие данные о численности населения
Центрального федерального округа РФ на 01.01.2002 г. в
разрезе областей (млн.чел):
1,5 1,2 2,2 1,6 1,9 1,1 0,9 1,8
1,6 0,8 1,3 1,1 1,2 2,1 2,4 1,3
Построить структурную группировку с равными
открытыми интервалами
Решение
Границы
Количество интервалов n = 4
Менее 1,2
Величина интервала h = 0,4
1,2 – 1,6
1,6 – 2,0
2,0 и более
19.
ПримерКоличество
областей
Менее 1,2
4
1,2 – 1,6
5
1,6 – 2,0
4
2,0 и более
3
Границы
20.
ПримерДана информация о рабочих одной из бригад
Тарифный 4
3
4
5
3
5
5
4
5
5
4
разряд
Дневная
выработка
140 100 120 200 120 170 140 120 180 160 160
деталей,
шт.
Построить аналитическую группировку. В качестве
факторного признака взять тарифный разряд, в
качестве результативного – дневную выработку
21.
ПримерТарифный
разряд
3
4
5
Число
рабочих
2
4
5
11
Дневная выработка деталей
одним рабочим, x, шт
110
120, 120, 140, 160
140, 160, 170, 180, 200
22.
Эмпирическая функция распределенияПолигон
Гистограмма
23.
Первичный анализЭмпирическая функция распределения случайной
величины ξ – частота того, что величина ξ примет
значение, меньшее, чем аргумент функции.
Определяется формулой:
Анализ рядов распределения наглядно можно
проводить на основе их графического изображения.
Для этой цели строят графики — полигон и
гистограмму частот.
24.
ПримерНа телефонной станции проводились наблюдения над
числом неправильных соединений в минуту.
Наблюдения в течение 30 минут дали результаты,
приведенные в таблице
Построить дискретный вариационный ряд и
выборочную функцию распределения
3
0
1
5
1
2
4
5
3
4
2
4
2
0
2
3
1
3
2
1
4
3
0
2
1
0
4
2
3
2
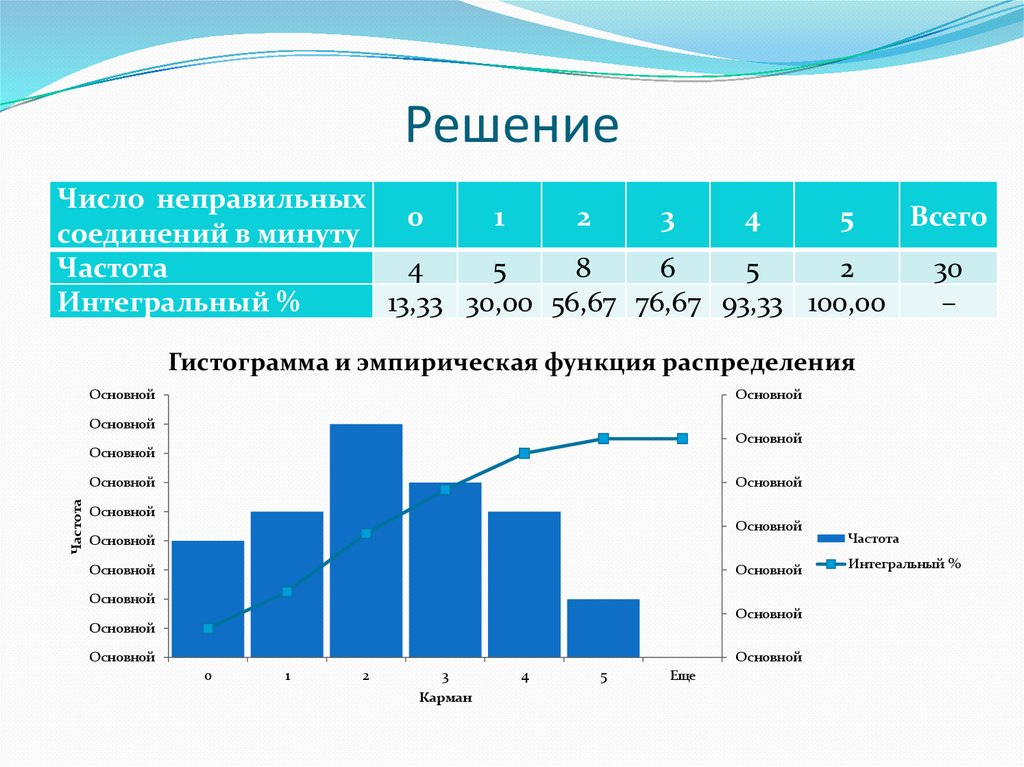
25.
РешениеЧисло неправильных
0
1
2
3
4
5
Всего
соединений в минуту
Частота
4
5
8
6
5
2
30
Интегральный %
13,33 30,00 56,67 76,67 93,33 100,00
–
Гистограмма и эмпирическая функция распределения
Основной
Основной
Основной
Основной
Основной
Частота
Основной
Основной
Основной
Основной
Основной
Основной
Основной
Основной
Основной
Основной
Основной
Основной
0
1
2
3
Карман
4
5
Еще
Частота
Интегральный %
26.
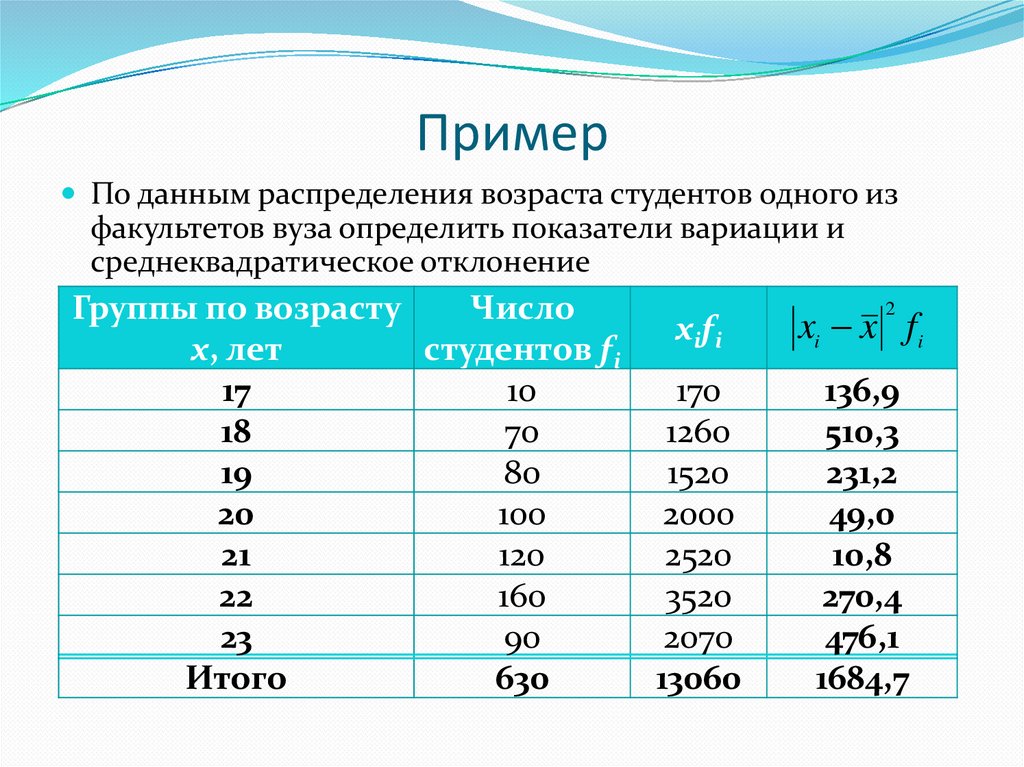
ПримерИсследуется рост учащихся (в сантиметрах) в
студенческой группе из 25 человек. Получена выборка
из 25 значений
Построить выборочную функцию распределения.
184 182 182 180 177 178 185 173 179 165
179 173 179 192 173 179 173 179 166 170
190 163 177 186 170
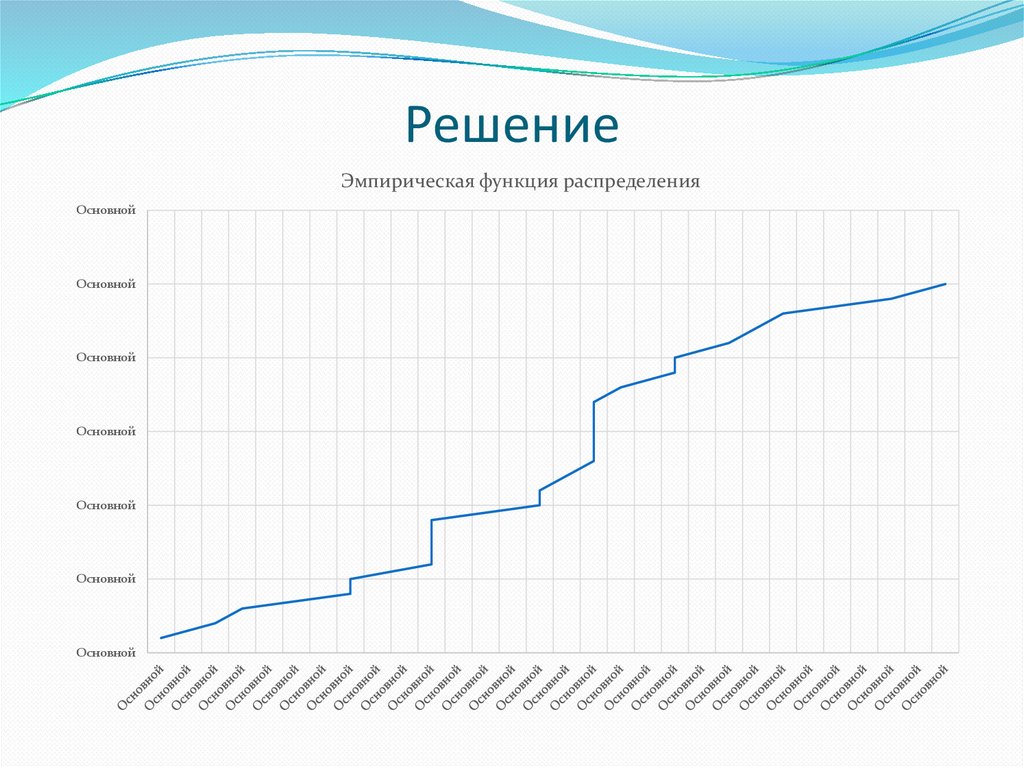
27.
РешениеЭмпирическая функция распределения
Основной
Основной
Основной
Основной
Основной
Основной
Основной
28.
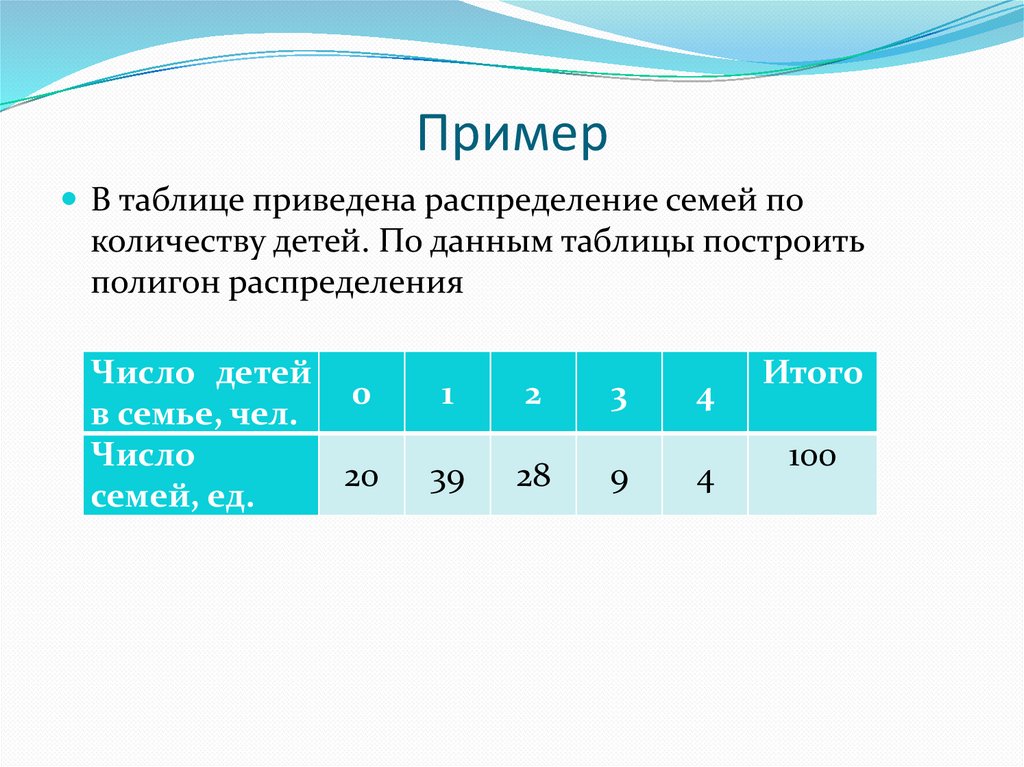
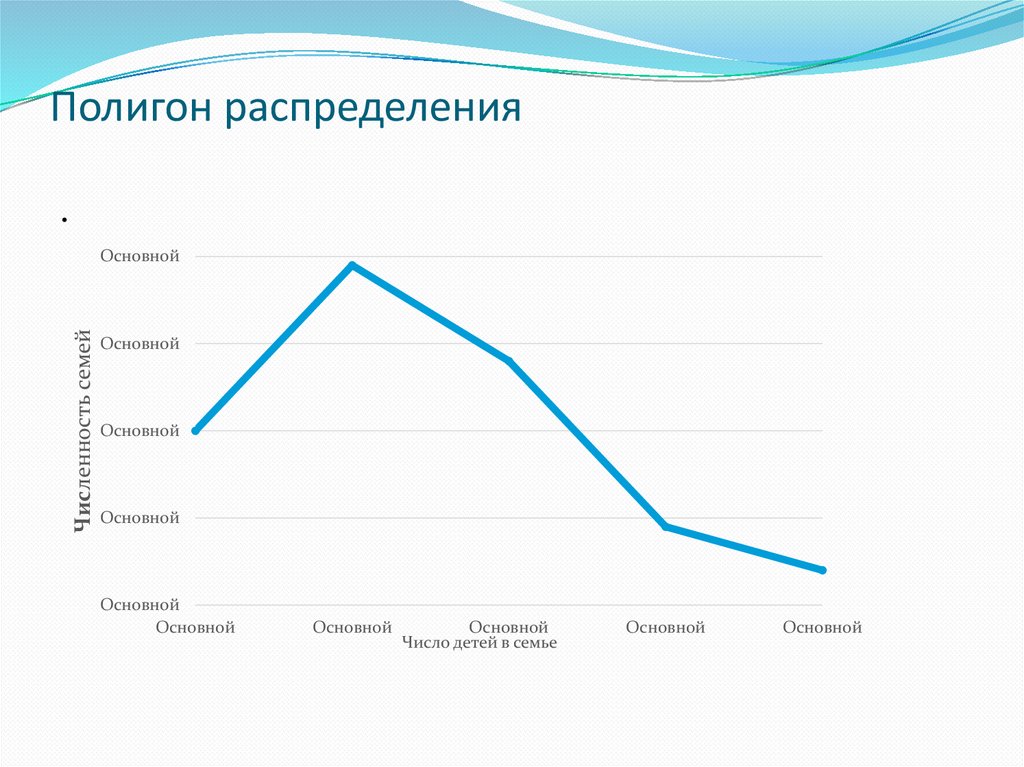
ПримерВ таблице приведена распределение семей по
количеству детей. По данным таблицы построить
полигон распределения
Число детей
0
в семье, чел.
Число
20
семей, ед.
1
39
2
28
3
9
4
4
Итого
100
29.
Полигон распределения.
Численность семей
Основной
Основной
Основной
Основной
Основной
Основной
Основной
Основной
Число детей в семье
Основной
Основной
30.
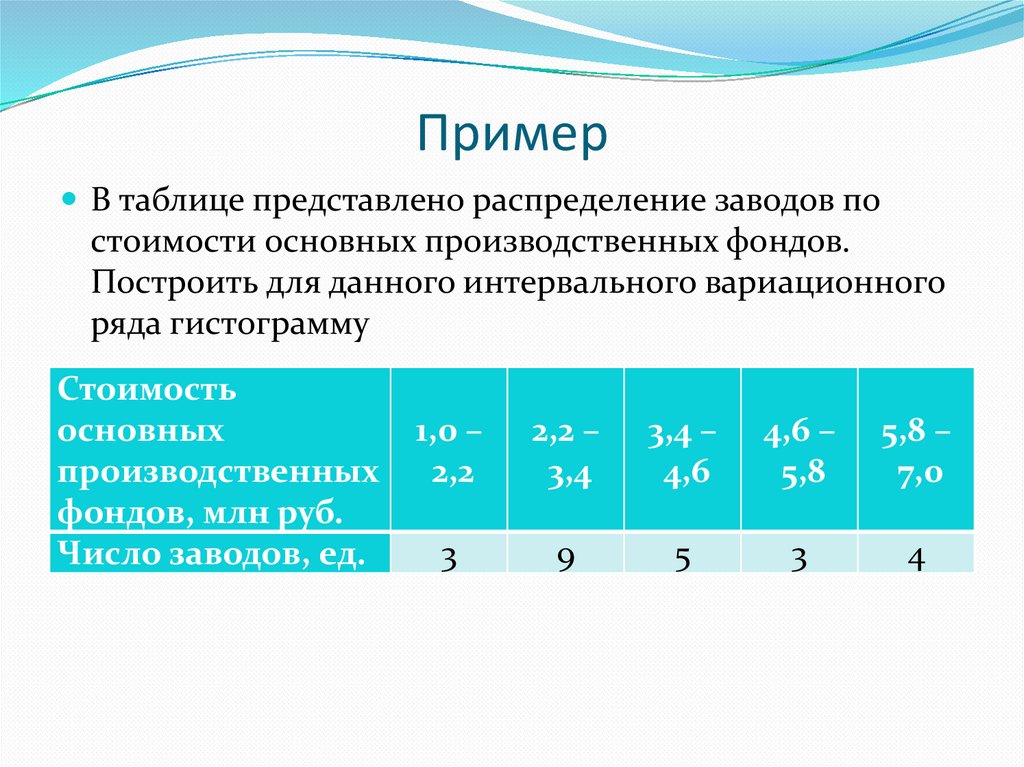
ПримерВ таблице представлено распределение заводов по
стоимости основных производственных фондов.
Построить для данного интервального вариационного
ряда гистограмму
Стоимость
основных
производственных
фондов, млн руб.
Число заводов, ед.
1,0 –
2,2
2,2 –
3,4
3,4 –
4,6
4,6 –
5,8
5,8 –
7,0
3
9
5
3
4
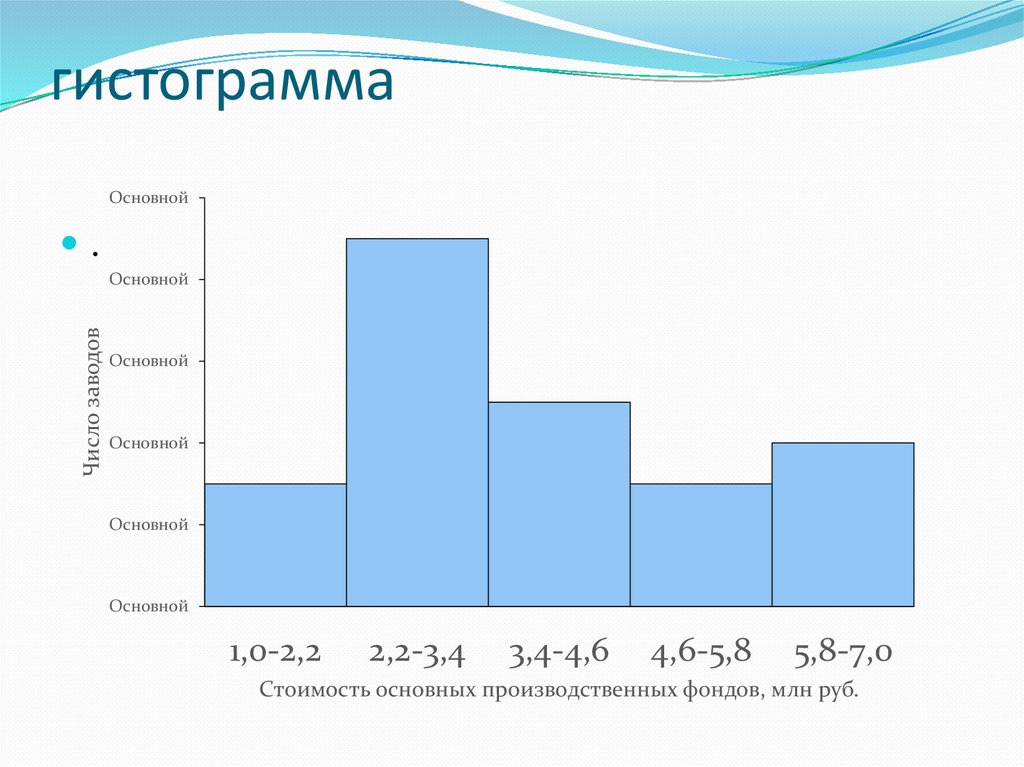
31.
гистограммаОсновной
.
Число заводов
Основной
Основной
Основной
Основной
Основной
1,0-2,2
2,2-3,4
3,4-4,6
4,6-5,8
5,8-7,0
Стоимость основных производственных фондов, млн руб.
32.
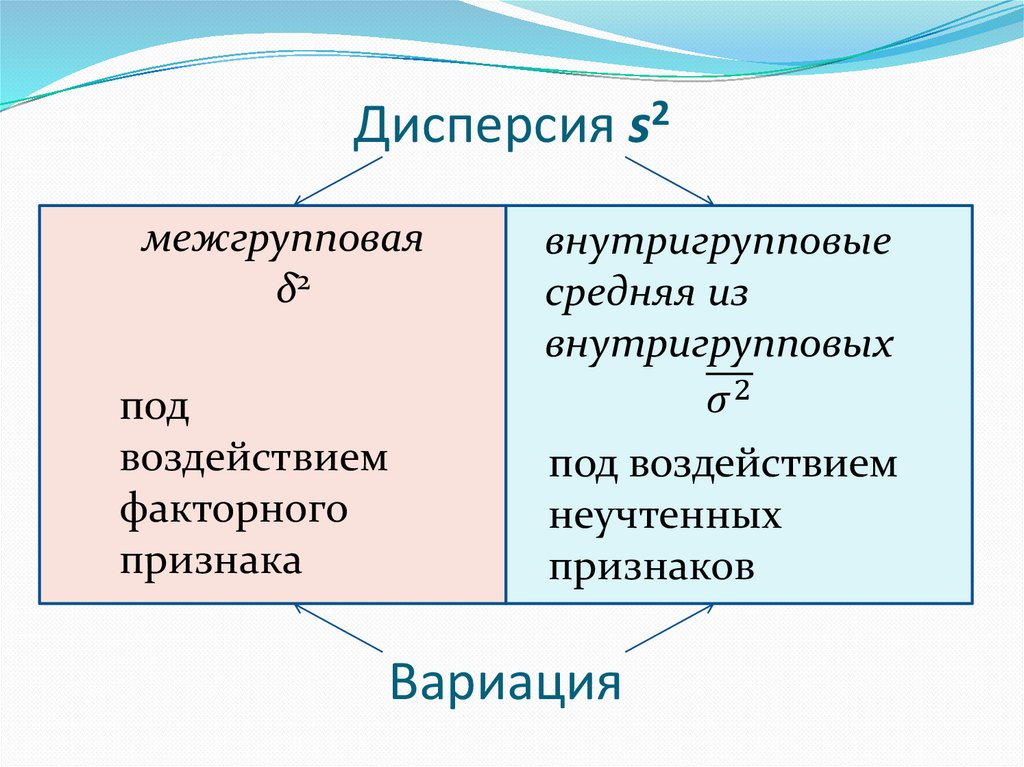
Частотные показателиПоказатели центра
Показатели вариации
Показатели формы
33.
Частотные показателичастота (f i)
частость или относительная частота (di)
кумулятивная (накопленная) частота (si) – объем
совокупности, со значениями вариантов не
превосходящих xi
плотность частоты (qi) – частота на единицу
интервала. Данный показатель используется, если
интервалы неравные и необходимо построить
гистограмму, а также при расчете Моды
34.
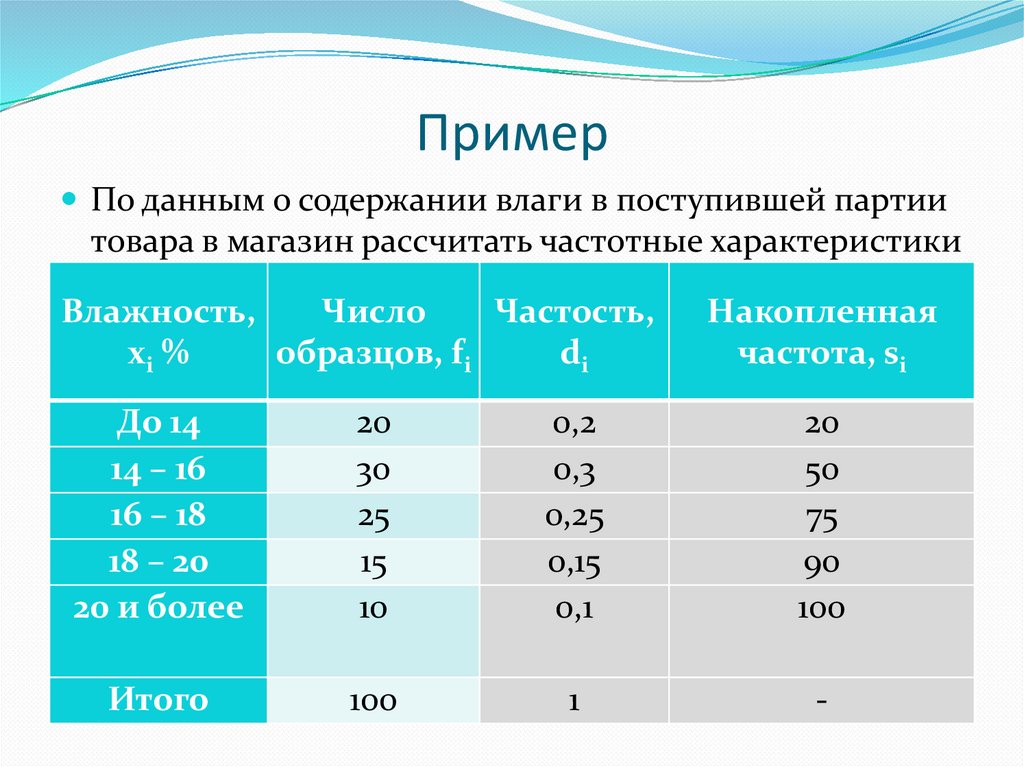
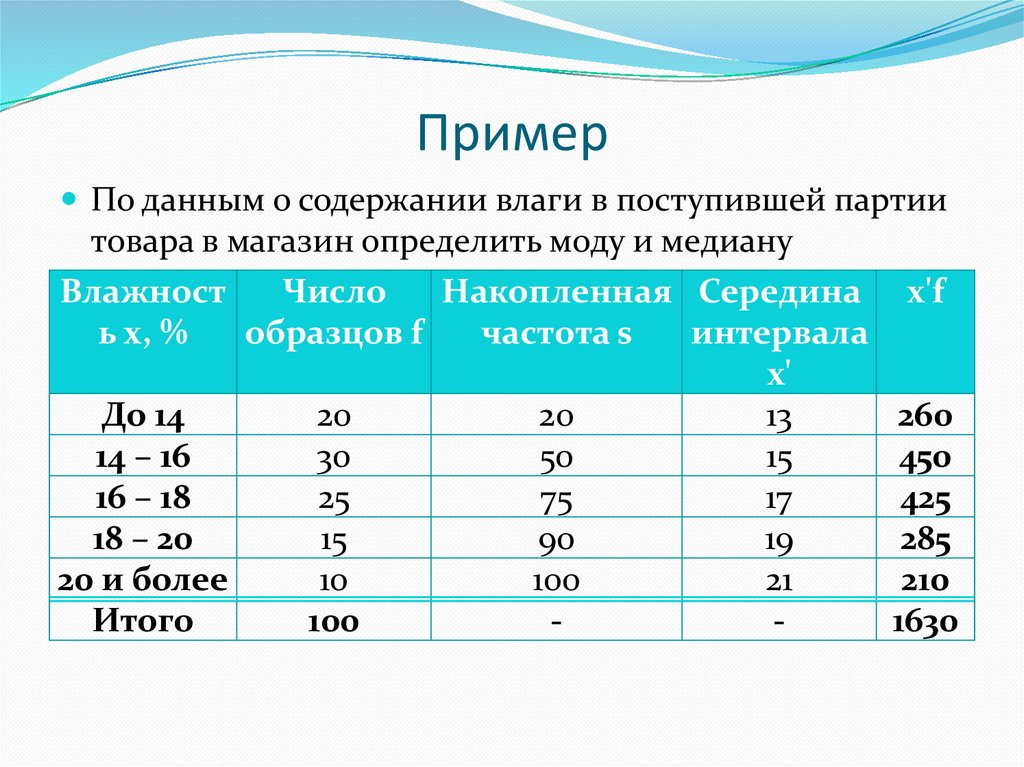
ПримерПо данным о содержании влаги в поступившей партии
товара в магазин рассчитать частотные характеристики
Влажность,
Число
Частость,
xi %
образцов, fi
di
Накопленная
частота, si
До 14
14 – 16
16 – 18
18 – 20
20 и более
20
30
25
15
10
0,2
0,3
0,25
0,15
0,1
20
50
75
90
100
Итого
100
1
-
35.
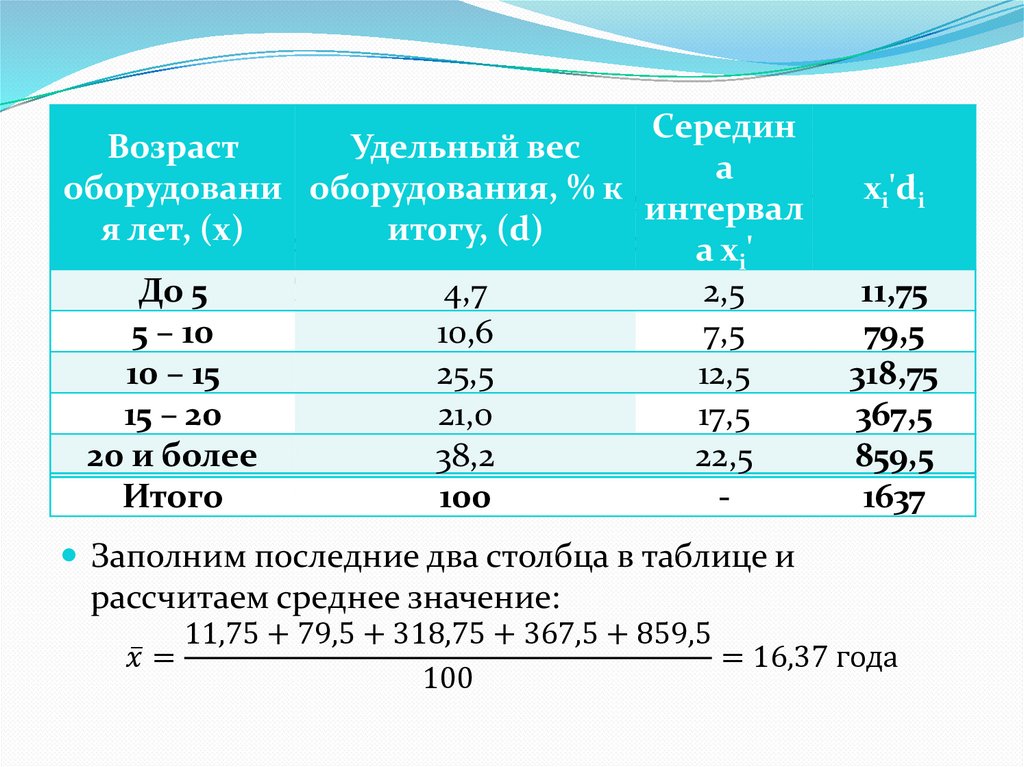
Показатели центра распределенияСреднее значение характеризует типичный уровень
признака в совокупности
для не сгруппированного ряда вычисляется как
среднее арифметическое
1 n
x xi
n i 1
для сгруппированного ряда – как среднее
взвешенное
k
x
x f
i 1
k
i
f
i 1
i
k
xi d i
i 1
i
36.
ПримерДана таблица взаимосвязи зарплаты рабочих и фонда
заработной платы
Заработная плата, тыс.
Фонд заработной платы,
руб.
тыс. руб.
10
300
30
150
50
100
Итого
550
Средняя зарплата ищется не как среднее
арифметическое (22,73), а как среднее гармоническое
300 + 150 + 100 550
=
= 14,86
300 150 100
37
+
+
10
30
50
37.
ПримерДана таблица темпов роста цен на жилье
Год Темп роста
2010
1,6
2011
0,9
2012
1,2
2013
1,3
Средний темп роста вычисляется как среднее
геометрическое
4






















































 mathematics
mathematics








