Similar presentations:
Математические основы статистики
1.
РАНХГСк.т.н., доцент
Куприянов В.Е.
2.
Лекция по теме № 2«Математические
основы статистики»
3.
Учебные вопросыЛекции по теме № 2
1) Основы теории вероятностей.
2) Основы математической
статистики.
4.
1. Основы теории вероятностей.Математическая основа статистики теория вероятностей.
ØТеория вероятностей есть математическая наука,
изучающая
закономерности
в
случайных
явлениях.
ØСлучайное явление — это такое явление, которое
при неоднократном воспроизведении одного и
того же опыта протекает каждый раз несколько
по-иному.
ØСлучайное событие - всякий факт, который в
результате опыта может произойти или не
произойти.
5.
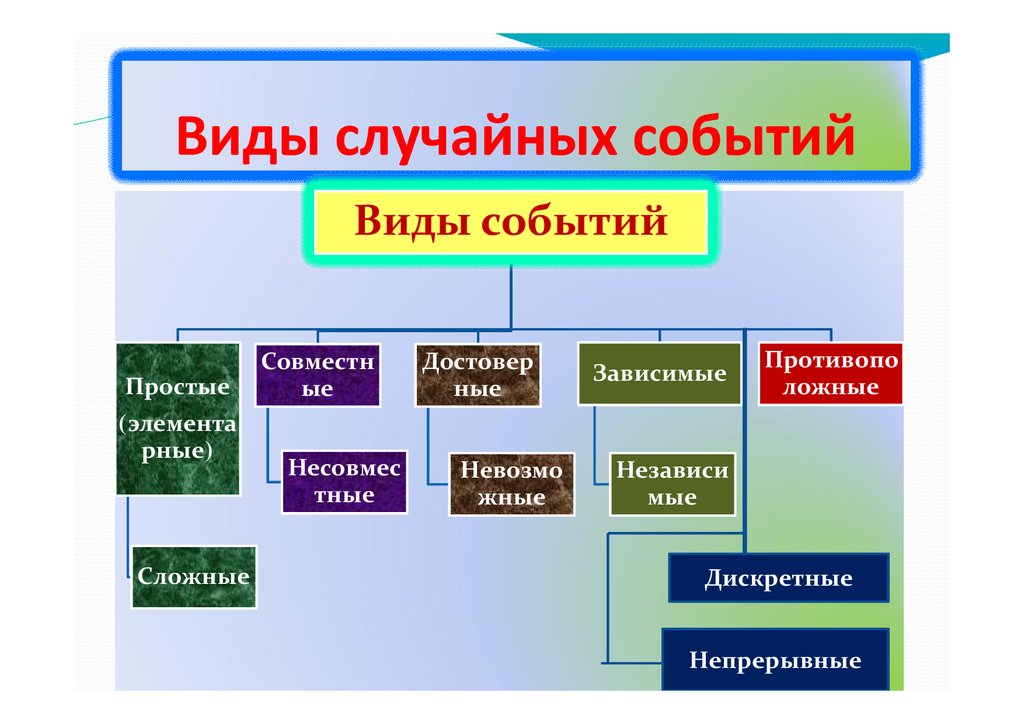
Виды случайных событийВиды событий
Простые
(элемента
рные)
Сложные
Совместн
ые
Несовмес
тные
Достовер
ные
Невозмо
жные
Зависимые
Противопо
ложные
Независи
мые
Дискретные
Непрерывные
6.
Виды случайных событийØПростое (элементарное) событие – каждый из
возможных результатов опыта.
ØСложное событие – событие, состоящее из 2-х и
более простых событий.
ØВсе события принято обозначать – буквами
латинского алфавита A, B, C, D или A1, A2, A3 …
B1, B2, B3 …
ØСлучайная величина – это величина, которая в
результате опыта (испытания) примет одно и
только одно возможное значение, наперед не
известное и зависящее от случайных причин,
которые заранее не могут быть учтены.
7.
Виды случайных событийØДискретное
событие
(дискретная
случайная
величина) - событие (величина), которое(ая)
принимает отдельные, изолированные возможные
значения с определенными вероятностями.
— Число возможных значений дискретной случайной
величины может быть конечным или бесконечным.
ØНепрерывной называют случайную величину,
которая может принимать все значения из
некоторого конечного или бесконечного
промежутка.
— Число возможных значений непрерывной
случайной величины бесконечно.
8.
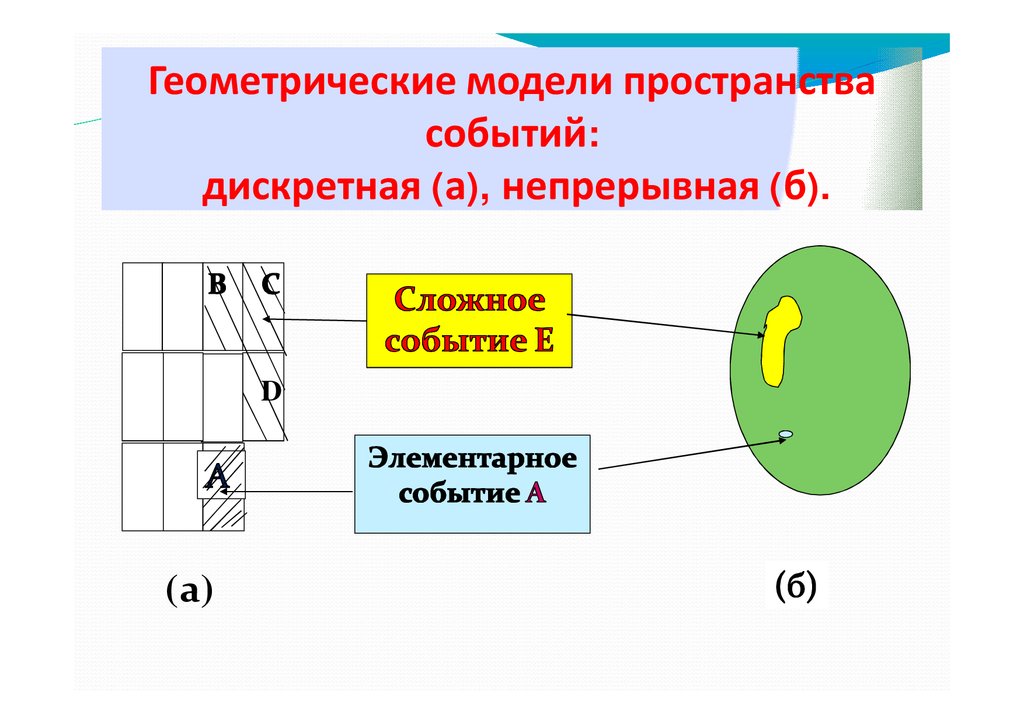
Геометрические модели пространствасобытий:
дискретная (а), непрерывная (б).
D
(а)
9.
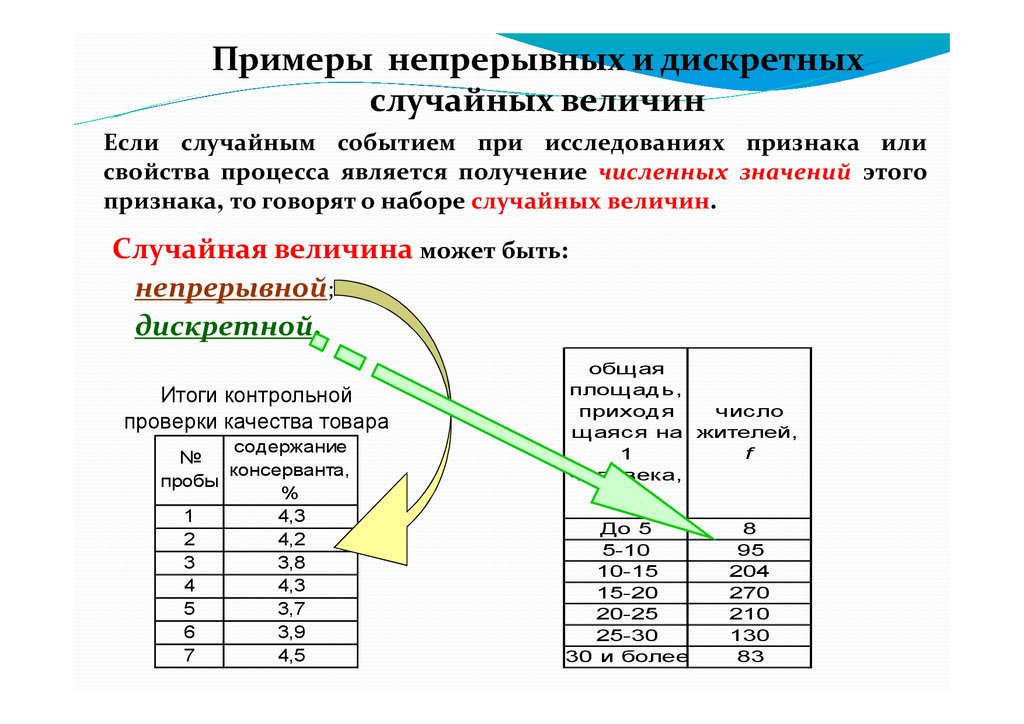
Примеры непрерывных и дискретныхслучайных величин
Если случайным событием при исследованиях признака или
свойства процесса является получение численных значений этого
признака, то говорят о наборе случайных величин.
Случайная величина может быть:
ü непрерывной;
ü дискретной.
Итоги контрольной
проверки качества товара
содержание
№
консерванта,
пробы
%
1
4,3
2
4,2
3
3,8
4
4,3
5
3,7
6
3,9
7
4,5
общ ая
площ адь,
приходя
число
щ аяся на жителей,
f
1
человека,
кв.м
До 5
5-10
10-15
15-20
20-25
25-30
30 и более
8
95
204
270
210
130
83
10.
Виды случайных событий— События
называют
совместными,
если
появление одного из них не исключает
появление других событий в одном и том же
испытании.
— События называют несовместными,
если
появление одного из них исключает появление
других событий в одном и том же испытании.
— Событие
достоверно,
если
каждый
элементарный
исход
испытания
благоприятствует этому событию.
— Событие невозможно, если ни один из
элементарных
исходов
испытания
не
благоприятствует этому событию.
11.
Виды случайных событий— Событие А называется независимым от
события В, если вероятность события А не
зависит от того, произошло событие В или нет.
— Событие А называется зависимым от события
В, если вероятность события А меняется в
зависимости от того, произошло событие В или
нет.
— Противоположными называют два единственно
возможных события, образующих полную
группу.
— Несколько событий образуют полную группу
событий, если в результате испытания появится
хотя бы одно из них.
12.
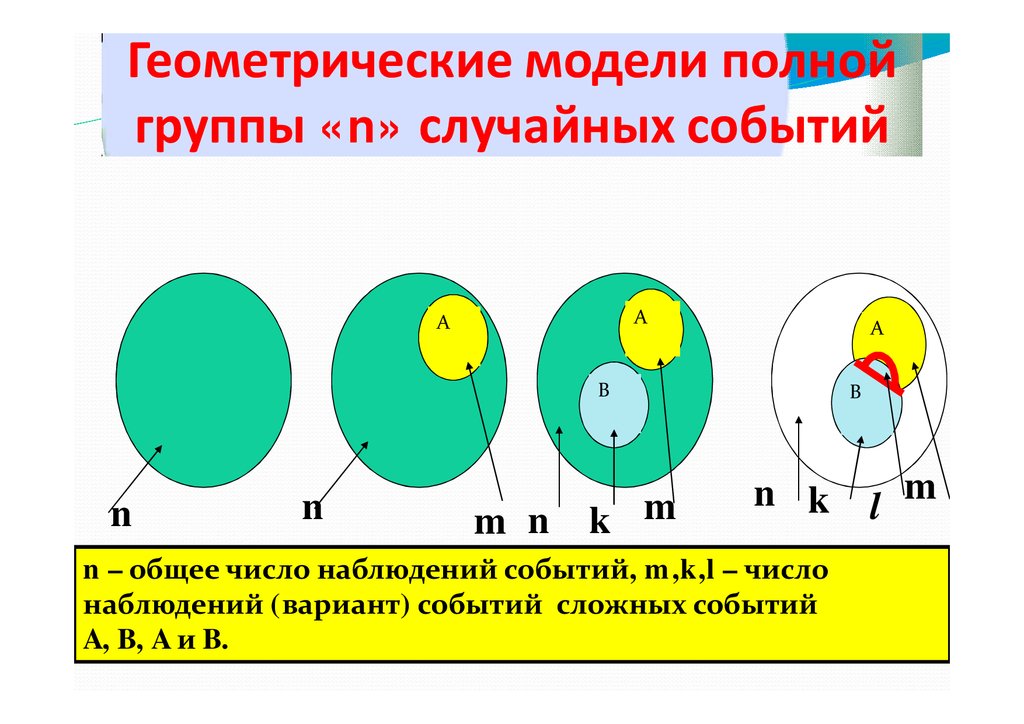
Геометрические модели полнойгруппы «n» случайных событий
A
A
A
B
n
n
m n k m
B
n k l m
n – общее число наблюдений событий, m,k,l – число
наблюдений (вариант) событий сложных событий
A, B, A и B.
13.
Определение вероятностиE Вероятность (в общем случае) есть число,
характеризующее
степень
объективной
возможности появления события.
— Классическое определение вероятности:
E Вероятностью наступления события А называют
отношение числа благоприятствующих этому
событию исходов (m) к общему числу всех
равновозможных несовместных элементарных
исходов, образующих полную группу (n).
m
p ( A) =
n
14.
Определение вероятности— Относительной частотой события W(A) называют
отношение числа испытаний, в которых событие
появилось (m), к общему числу фактически
произведенных испытаний (n).
W(A)= m/n
Статистическое определение вероятности
E Вероятность события
есть относительная
частота или число, близкое к ней.
m
lim = p ( A) ≈ W ( A)
n →∞ n
15.
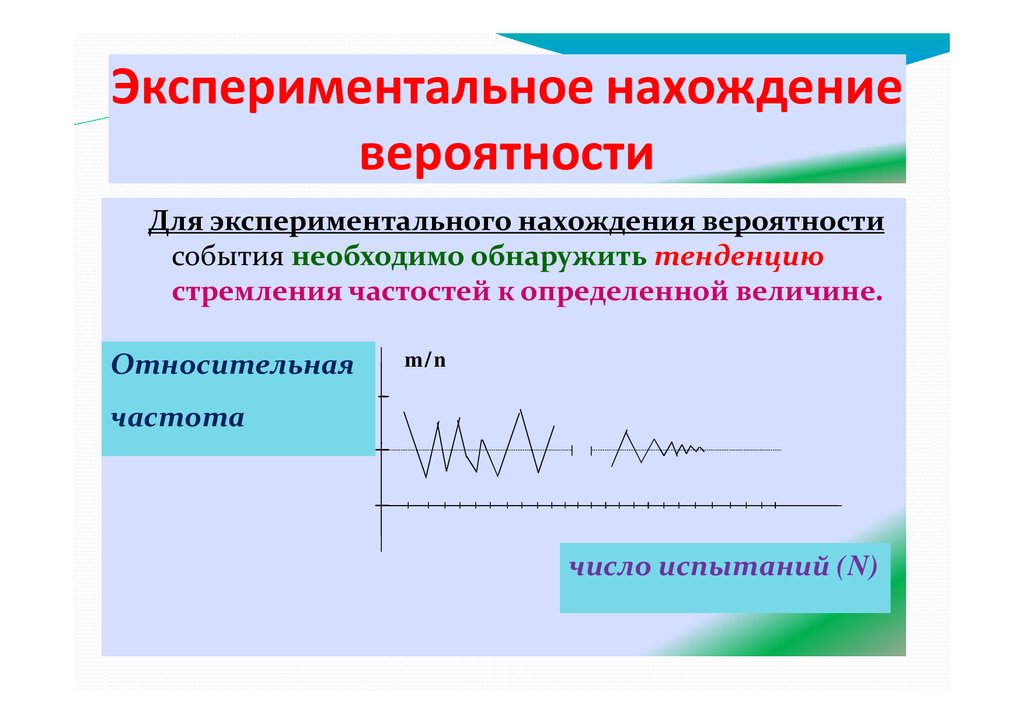
Экспериментальное нахождениевероятности
Для экспериментального нахождения вероятности
события необходимо обнаружить тенденцию
стремления частостей к определенной величине.
Относительная
m/n
частота
число испытаний (N)
16.
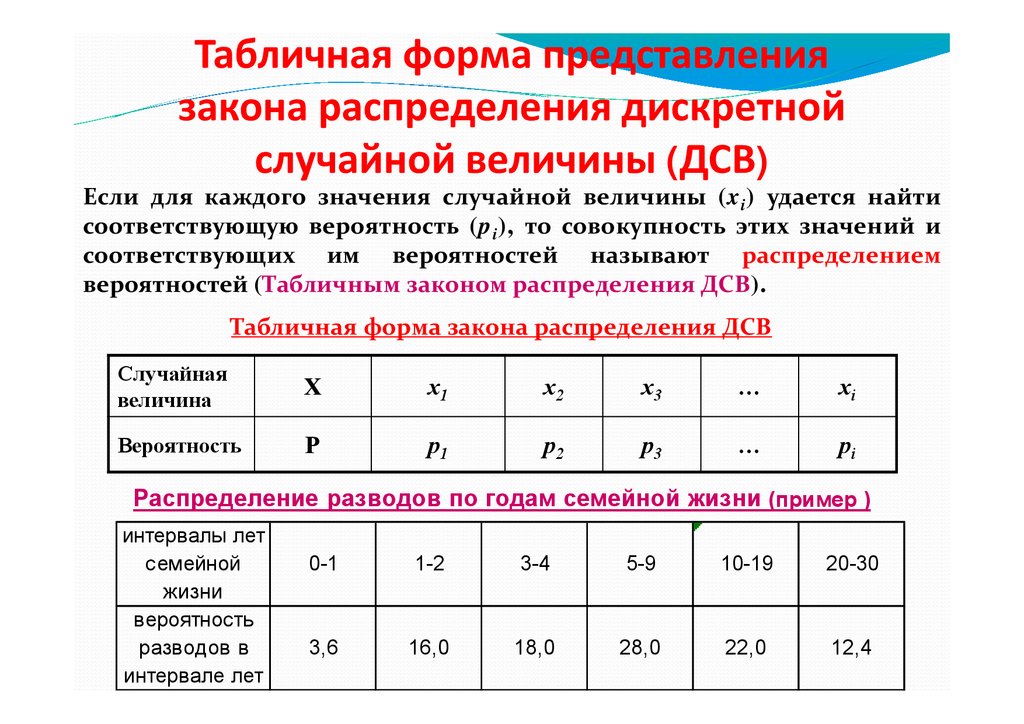
Табличная форма представлениязакона распределения дискретной
случайной величины (ДСВ)
Если для каждого значения случайной величины (xi) удается найти
соответствующую вероятность (pi), то совокупность этих значений и
соответствующих им вероятностей называют распределением
вероятностей (Табличным законом распределения ДСВ).
Табличная форма закона распределения ДСВ
Случайная
величина
X
x1
x2
x3
…
xi
Вероятность
P
p1
p2
p3
…
pi
Распределение разводов по годам семейной жизни (пример )
интервалы лет
семейной
жизни
вероятность
разводов в
интервале лет
0-1
1-2
3-4
5-9
10-19
20-30
3,6
16,0
18,0
28,0
22,0
12,4
17.
Закон распределения непрерывнойслучайной величины
Если обозначить Δр – вероятность попадания случайной величины X
в интервал ее значений Δx, то можно рассчитать вероятность,
соответствующую единичному интервалу значений случайной
величины, т.е. вычислить отношение Δр/Δx.
∆p
= f (x) плотность вероятности (дифференциальный
∆x
закон распределения)
Распределение разводов по годам семейной жизни (пример)
интервалы лет
семейной
жизни
вероятность
разводов в
интервале лет
величина
интервала,
года
плотность
распределения разводов
0-1
1-2
3-4
5-9
10-19
20-30
3,6
16,0
18,0
28,0
22,0
12,4
1
1
1
4
9
10
3,60
16,00
18,00
7,00
2,44
1,24
18.
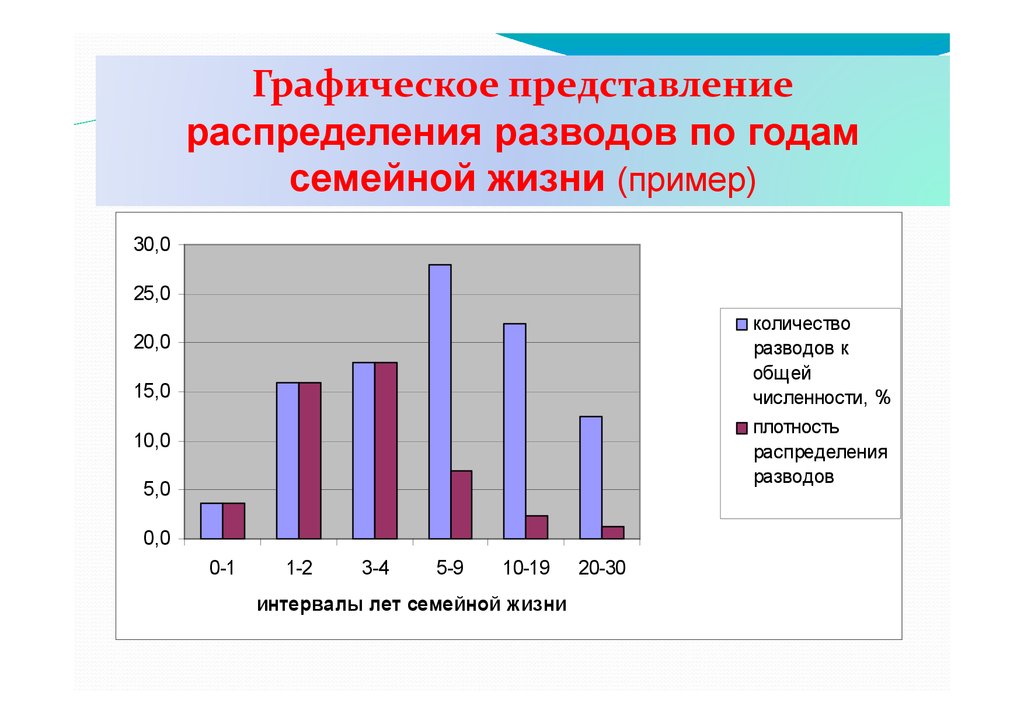
Графическое представлениераспределения разводов по годам
семейной жизни (пример)
30,0
25,0
количество
разводов к
общей
численности, %
плотность
распределения
разводов
20,0
15,0
10,0
5,0
0,0
0-1
1-2
3-4
5-9
10-19
интервалы лет семейной жизни
20-30
19.
2. Основы математическойстатистики
Наиболее распространенными методами обработки
и анализа первичной статистической информации
являются сводка и группировка данных.
Статистическая
сводка
это
Научно организационная обработка
материалов
статистического
наблюдения в целях получения
обобщенных
характеристик
изучаемого
явления
по
ряду
существенных для него признаков
Основные задачи статической сводки
Обработать данные
статистического
наблюдения
Дать характеристику всей совокупности
фактов при помощи обобщающих
статистических показателей
20.
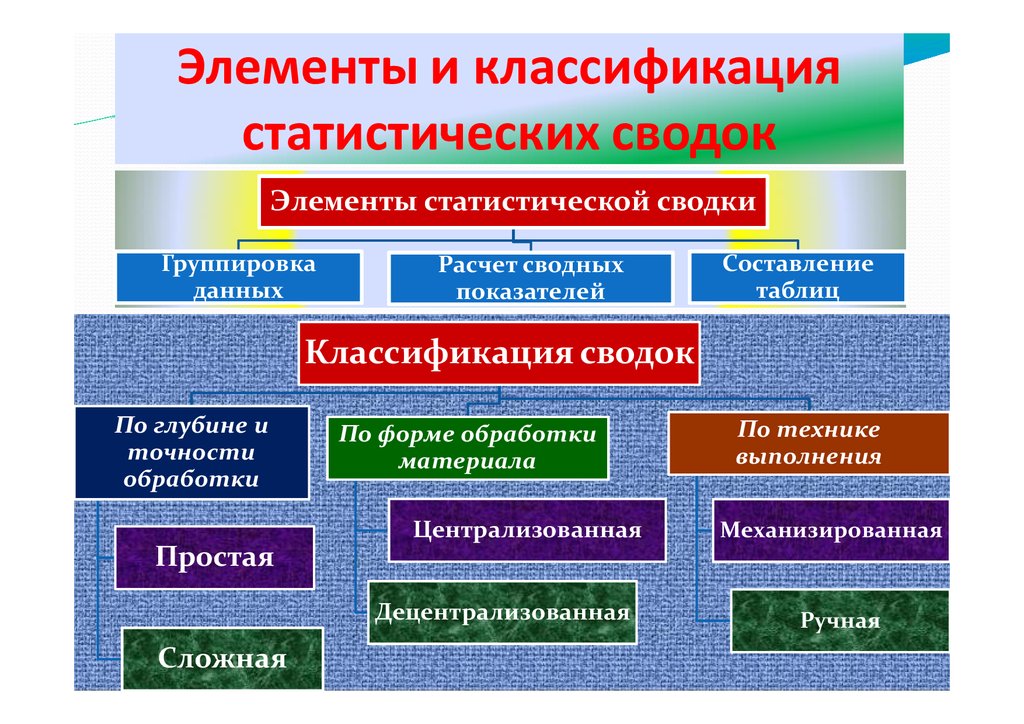
Элементы и классификациястатистических сводок
Элементы статистической сводки
Группировка
данных
Расчет сводных
показателей
Составление
таблиц
Классификация сводок
По глубине и
точности
обработки
Простая
По форме обработки
материала
Централизованная
Децентрализованная
Сложная
По технике
выполнения
Механизированная
Ручная
21.
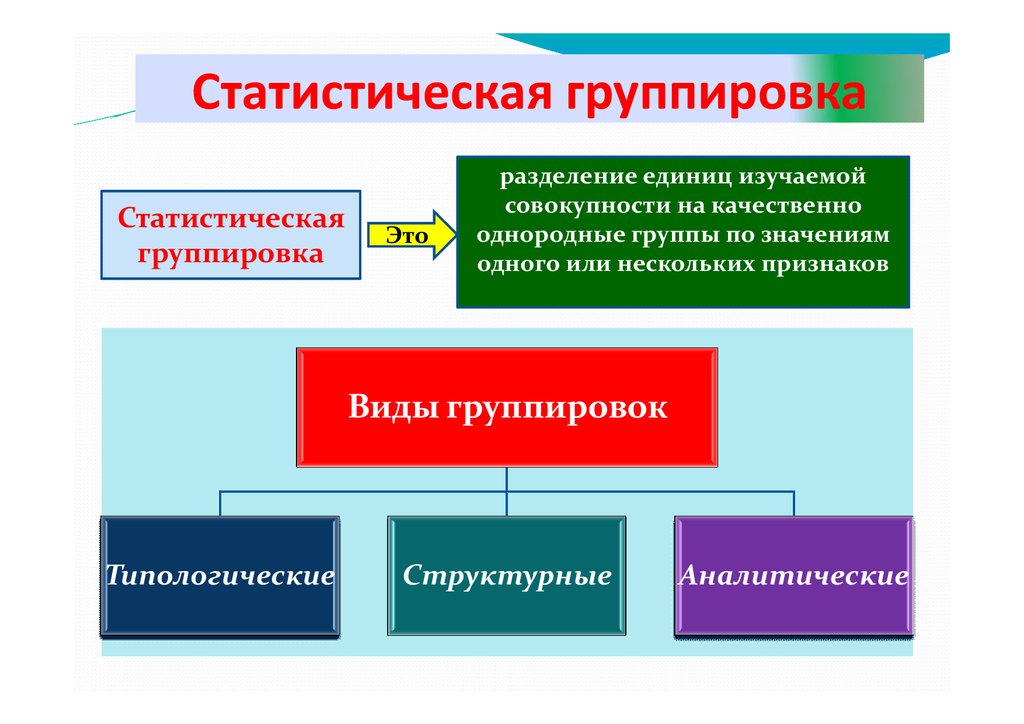
Статистическая группировкаСтатистическая
группировка
Это
разделение единиц изучаемой
совокупности на качественно
однородные группы по значениям
одного или нескольких признаков
Виды группировок
Типологические
Структурные
Аналитические
22.
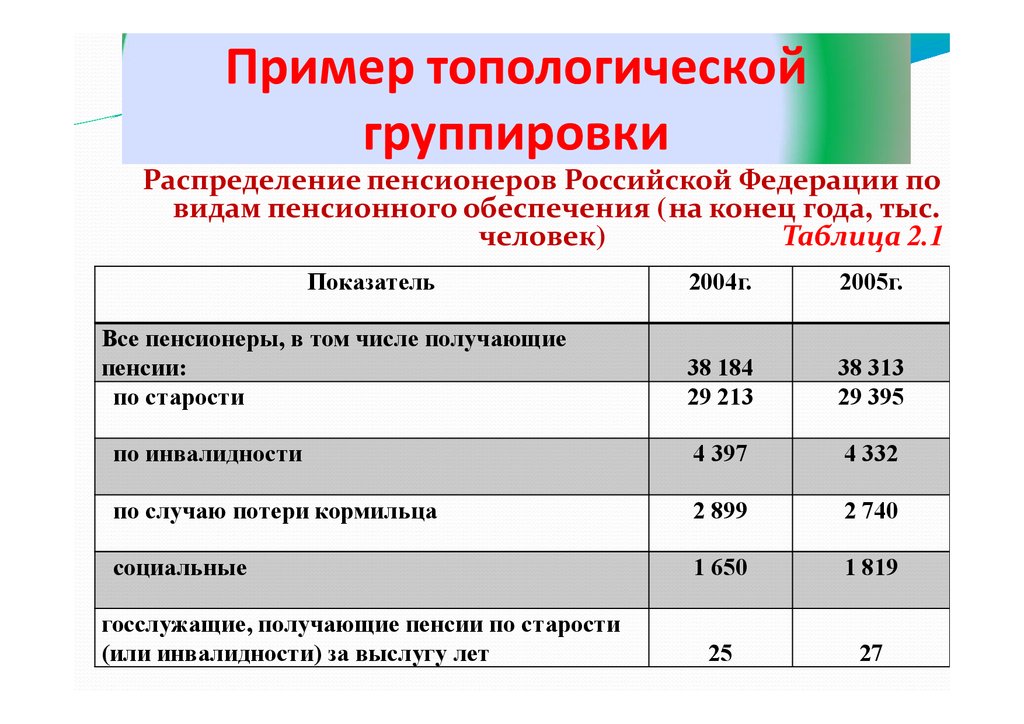
Пример топологическойгруппировки
Распределение пенсионеров Российской Федерации по
видам пенсионного обеспечения (на конец года, тыс.
человек)
Таблица 2.1
Показатель
2004г.
2005г.
38 184
29 213
38 313
29 395
по инвалидности
4 397
4 332
по случаю потери кормильца
2 899
2 740
социальные
1 650
1 819
25
27
Все пенсионеры, в том числе получающие
пенсии:
по старости
госслужащие, получающие пенсии по старости
(или инвалидности) за выслугу лет
23.
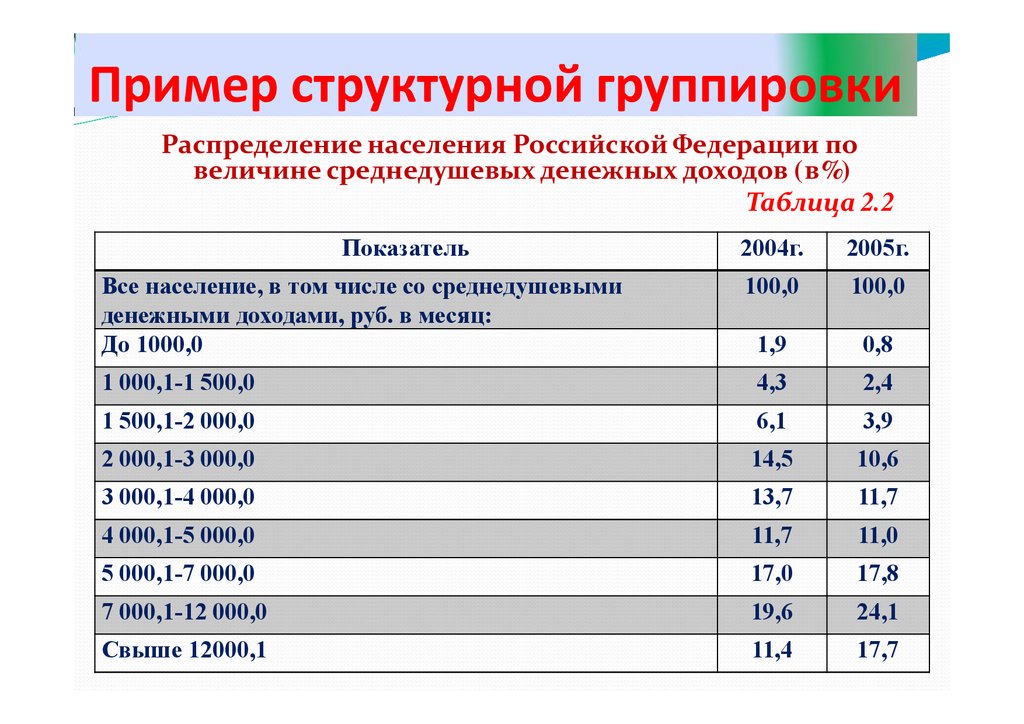
Пример структурной группировкиРаспределение населения Российской Федерации по
величине среднедушевых денежных доходов (в%)
Таблица 2.2
Показатель
2004г.
2005г.
100,0
100,0
1,9
0,8
1 000,1-1 500,0
4,3
2,4
1 500,1-2 000,0
6,1
3,9
2 000,1-3 000,0
14,5
10,6
3 000,1-4 000,0
13,7
11,7
4 000,1-5 000,0
11,7
11,0
5 000,1-7 000,0
17,0
17,8
7 000,1-12 000,0
19,6
24,1
Свыше 12000,1
11,4
17,7
Все население, в том числе со среднедушевыми
денежными доходами, руб. в месяц:
До 1000,0
24.
Пример аналитической группировкиРаспределение регионов по численности занятых в
экономике (данные условные) Таблица 2.3
гру
пп
ы
Группы регионов
по численности
занятых в
экономике, тыс.
человек
Число
регио
нов
А
Б
1
№
Численность занятых
в экономике.
тыс.чел.
Валовый
региональный
продукт, млрд.
руб.
всего
в
среднем
на один
регион
всего
в
среднем
на один
регион
1
2
3
4
5
220-350
4
1 240
310
107,1
26,8
2
350-480
9
3 645
405
285,3
31,7
3
480-610
11
6 028
548
383,9
34,9
4
610-740
7
4 767
681
245,7
35,1
5
740-870
5
4 000
800
192,0
38,4
36
19 680
547
1 214,0
33,7
Итого
25.
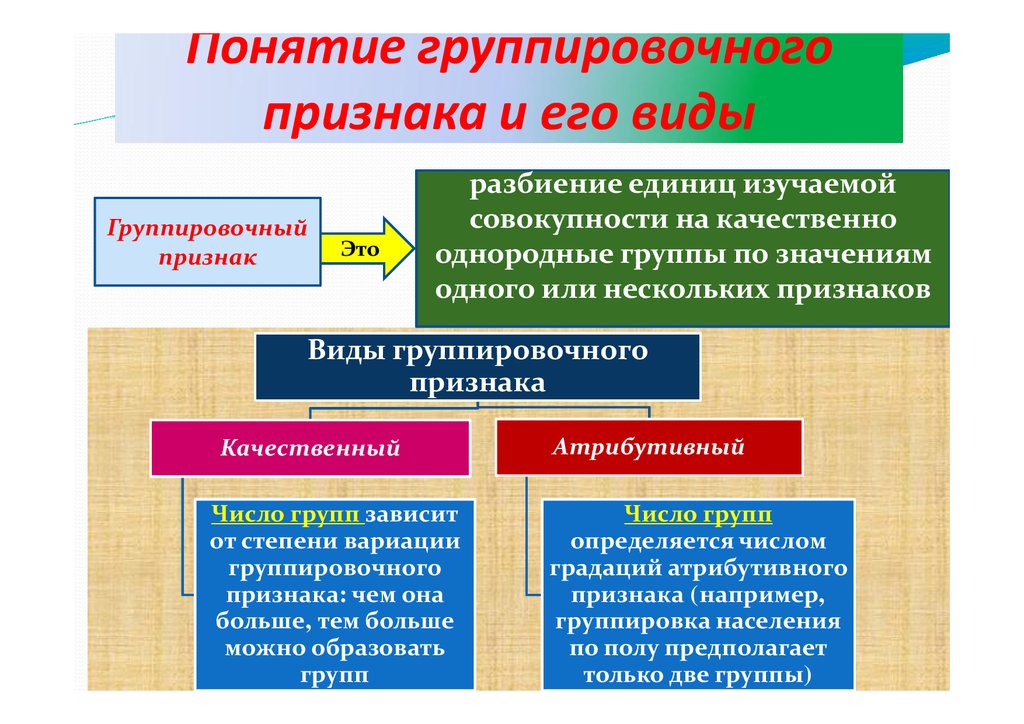
Понятие группировочногопризнака и его виды
Группировочный
признак
Это
разбиение единиц изучаемой
совокупности на качественно
однородные группы по значениям
одного или нескольких признаков
Виды группировочного
признака
Качественный
Число групп зависит
от степени вариации
группировочного
признака: чем она
больше, тем больше
можно образовать
групп
Атрибутивный
Число групп
определяется числом
градаций атрибутивного
признака (например,
группировка населения
по полу предполагает
только две группы)
26.
Формула определения числагрупп
Если основание группировки служит
количественный признак, то для определения
количества групп (группировка с равными
интервалами) можно воспользоваться
формулой американского ученого Стерджесса.
Формула
Стерджесса
n = 1 + 3,322 lgN,
где n – число групп;
N – число единиц
совокупности
(1)
27.
Понятие интервалагруппировки и его параметры
— Когда определенно число групп, то следует
установить интервалы группировки.
Интервал
группировки
Значение варьирующего признака,
лежащего в определенных границах
— Интервал имеет величину (ширину), верхнюю и
нижнюю границы или хотя бы одну их них.
— Нижняя граница интервала – это минимальное
значение признака, верхняя граница –
наибольшее значение признака в интервале.
— Величина интервала (ширина) представляет
собой разность между верхней и нижней
границами интервала.
28.
Классификация интерваловгруппировки
Виды интервалов группировки
Равные
Применяется
в тех случаях,
когда
вариация
признака
происходит в
сравнительно
узких
границах
более или
менее
равномерно
(см. табл. 2.3)
Неравные
Применяется
в тех случаях,
когда размах
вариации
признака в
совокупности
велик и
значения
признака
варьируют
неравномерно
(см. табл. 2.2)
Открытые
Интервал, у
которого
указана
только одна
граница:
верхняя – у
первого,
нижняя – у
последнего
(см. табл. 2.2)
Закрытые
Интервал, у
которого есть
верхняя и
нижняя
границы
(см. табл. 2.3)
29.
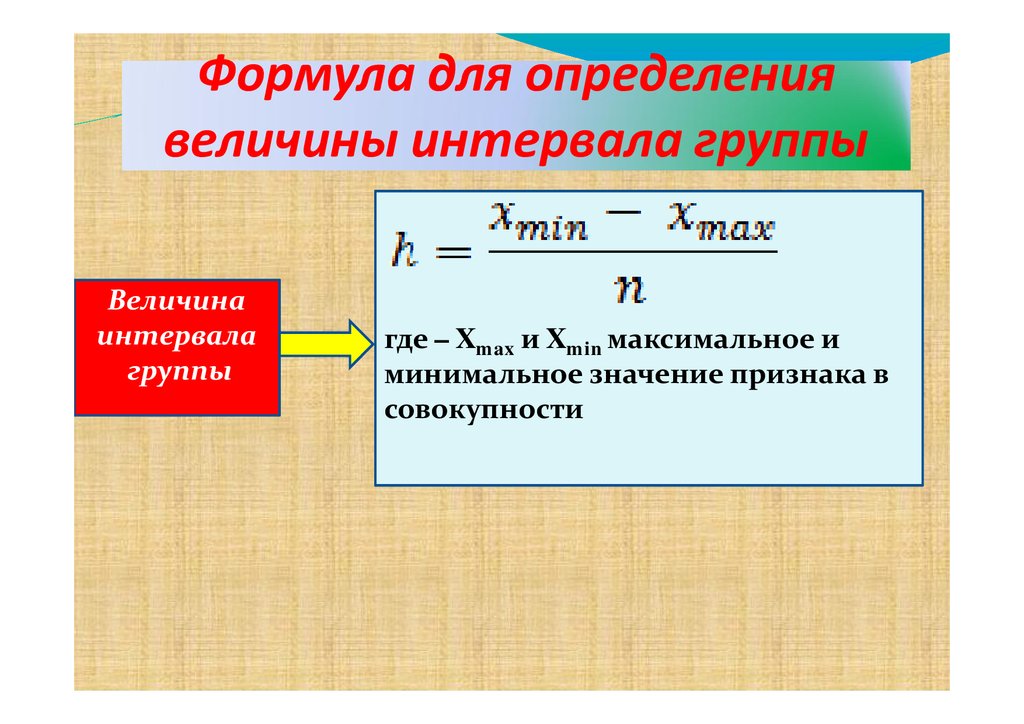
Формула для определениявеличины интервала группы
Величина
интервала
группы
где – Xmax и Xmin максимальное и
минимальное значение признака в
совокупности
30.
Правила определенияинтервала группировки
1. Если величина интервала, рассчитанная по формуле (2),
2.
3.
имеет один знак до запятой (например, 0,7; 0,58; 2,359),
то полученное значение следует округлить до десятых
(в приведенном примере это будут значения 0,7; 0,6;
2,4).
Если величина интервала, рассчитанная по формуле (2),
имеет две значащие цифры до запятой и несколько
после запятой (например, 11,2; 23,385), то это значение
следует округлить до целого числа (в указанном
примере это будут значения 11; 23).
Если величина интервала, рассчитанная по формуле (2),
представляет собой трехзначное число (например, 123;
757), то это число целесообразно округлить до
ближайшего числа, кратного 10 (в приведенном
примере это будут значения 120; 760)
31.
Правила определенияинтервала группировки
4. Если
интервал групп закрытые и основанием
группировки служит непрерывный признак, то нижняя
граница формируется по принципу «включительно», а
верхняя – по принципу «исключительная» (например,
если нижняя граница i – группы равна 50, а верхняя –
100, то единица совокупности со значением признака,
равным 100, попадает в группу i + 1 ) (табл. 2.3).
5. Если значения признака совпадает с границами
интервалов, то можно использовать открытые
интервалы, введя слова «до», «менее» и «более» (табл.
2.2).
6. Если в основании группировки лежит дискретный
признак, то верхняя граница i-го интервала равна
нижней границе (i + 1)-го интервала, увеличенной на 1
32.
Понятие статистическогоряда распределения
— После определения группировочного признака и
границ групп
распределения.
Статистический
ряд
распределения
строится
статистический
ряд
упорядоченной
распределение единиц
изучаемой совокупности на
группы по определенному
варьирующему признаку
33.
Виды рядов распределенияВиды рядов
распределения
Атрибутивные
(группы строятся
по качественному
признаку)
Вариационные
(группы строятся по
количественному
признаку)
Дискретные (группы
строятся по признаку,
изменяющему дискретно)
Интервальные
(группы строятся
по признаку,
принимающему в
определенном
интервале любые
значения)
34.
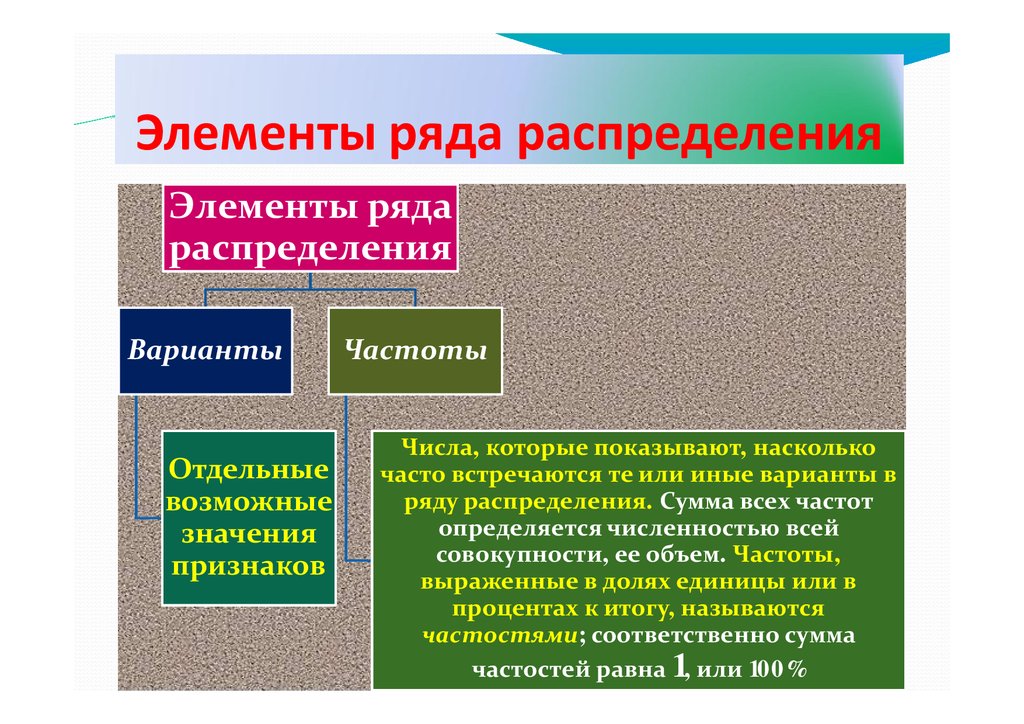
Элементы ряда распределенияЭлементы ряда
распределения
Варианты
Отдельные
возможные
значения
признаков
Частоты
Числа, которые показывают, насколько
часто встречаются те или иные варианты в
ряду распределения. Сумма всех частот
определяется численностью всей
совокупности, ее объем. Частоты,
выраженные в долях единицы или в
процентах к итогу, называются
частостями; соответственно сумма
частостей равна 1, или 100%
35.
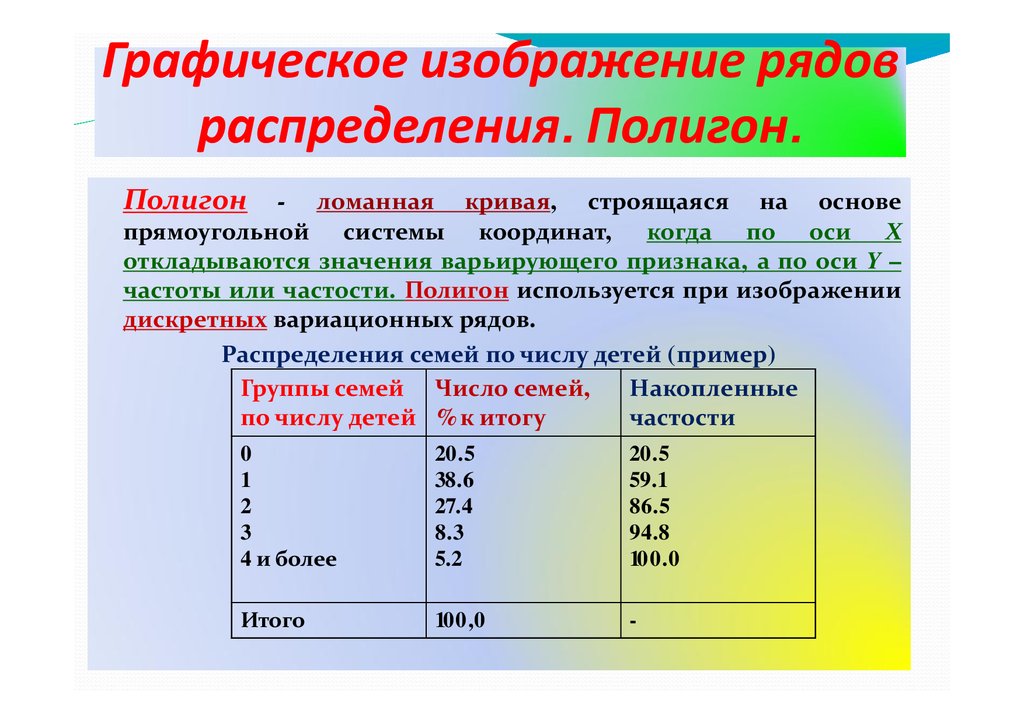
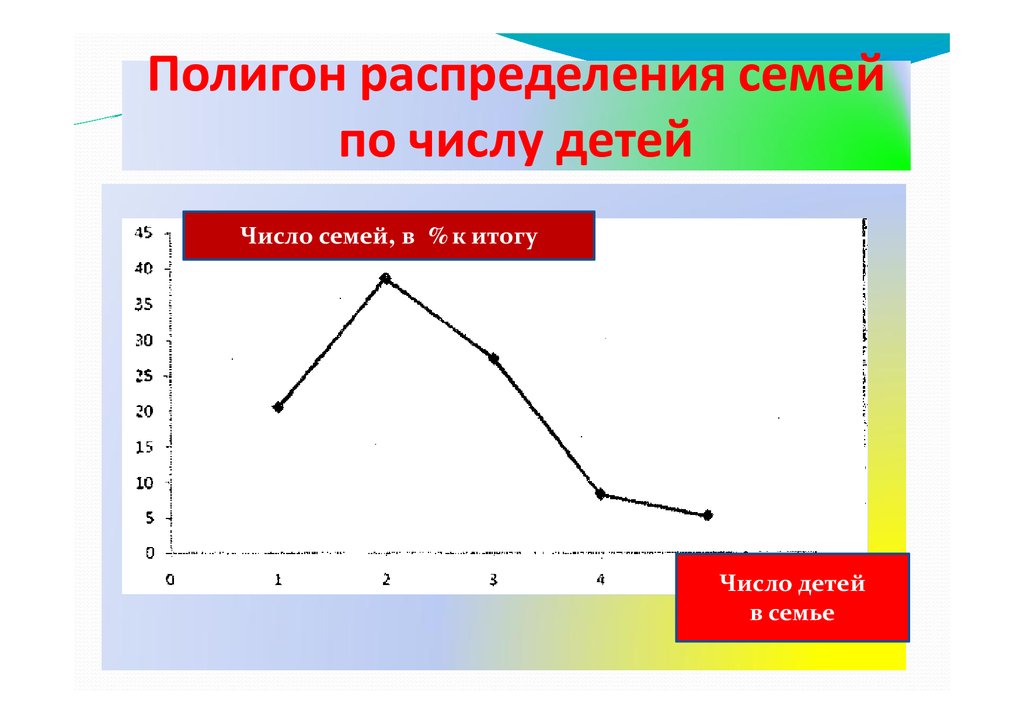
Графическое изображение рядовраспределения. Полигон.
— Полигон
- ломанная кривая, строящаяся на основе
прямоугольной системы координат, когда по оси Х
откладываются значения варьирующего признака, а по оси Y –
частоты или частости. Полигон используется при изображении
дискретных вариационных рядов.
Распределения семей по числу детей (пример)
Группы семей Число семей,
Накопленные
по числу детей % к итогу
частости
0
1
2
3
4 и более
20.5
38.6
27.4
8.3
5.2
20.5
59.1
86.5
94.8
100.0
Итого
100,0
-
36.
Полигон распределения семейпо числу детей
Число семей, в % к итогу
Число детей
в семье
37.
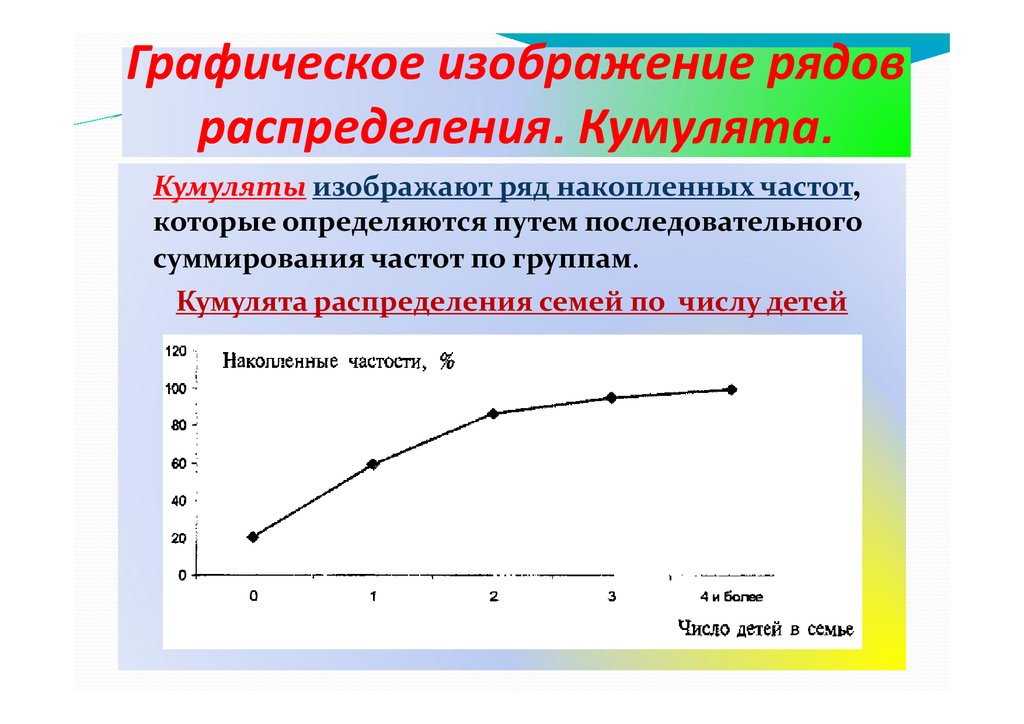
Графическое изображение рядовраспределения. Кумулята.
— Кумуляты изображают ряд накопленных частот,
которые определяются путем последовательного
суммирования частот по группам.
Кумулята распределения семей по числу детей
38.
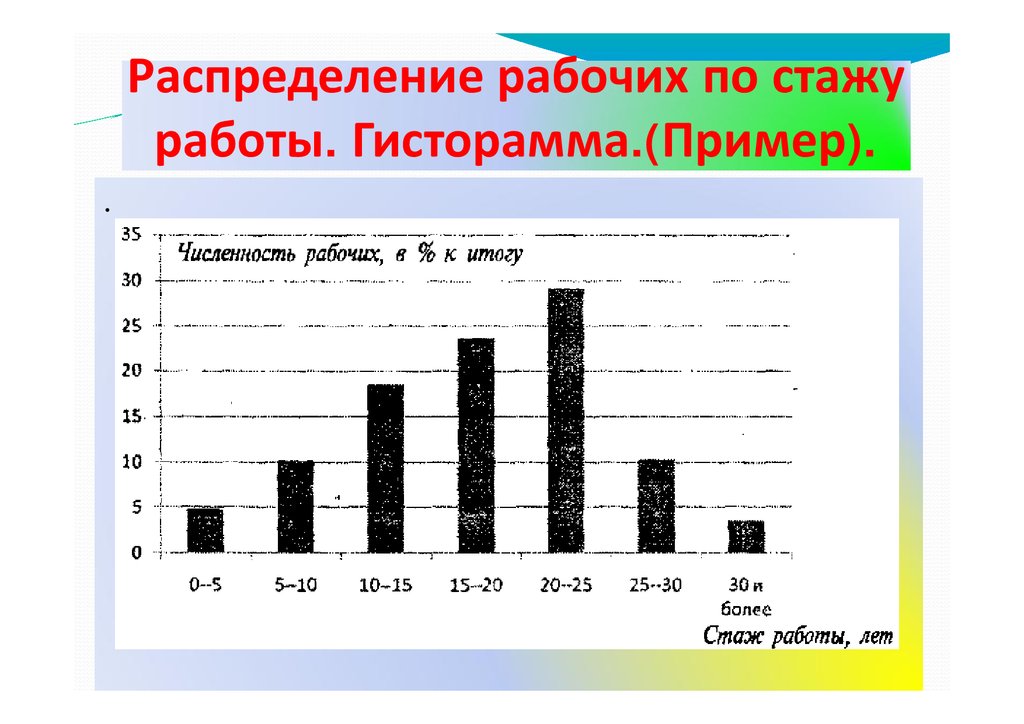
Графическое изображение рядовраспределения. Гистограмма.
Гистограмма применяется для изображения
интервального вариационного ряда. При построении
гистограммы на оси абсцисс откладываются величины
интервалов, а частоты изображаются
прямоугольниками, построенными на
соответствующих интервалах.
Распределение рабочих по стажу работы (пример)
39.
Распределение рабочих по стажуработы. Гисторамма.(Пример).
.
40.
Понятие средней величины,виды средних величин
Средняя
величина
Это
Обобщающий показатель, который дает
количественную характеристику признака
в статистической совокупности в условиях
конкретного места и времени
Виды средних величин
Степенные
Гармоническая
Геометрическая
Структурные
Мода
Медиана
Арифметическая
Квартили
Квадратическая
Децили
Кубическая
Квинтили
41.
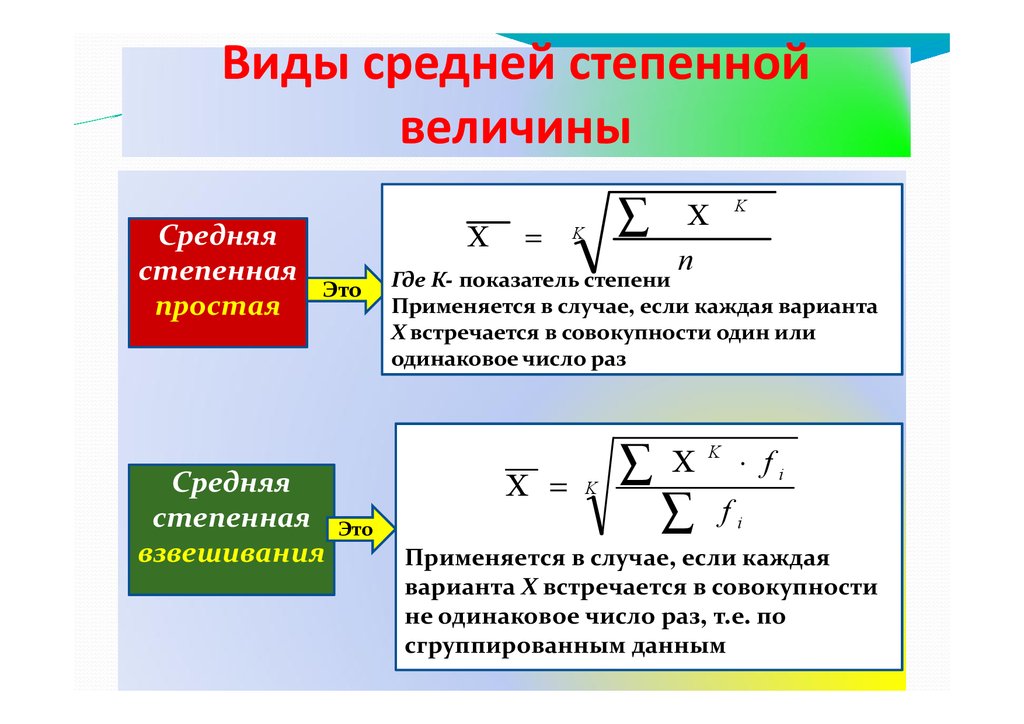
Виды средней степеннойвеличины
∑
где
Средняя
степенная
простая
Χ
Это
Средняя
степенная
взвешивания
=
K
n
Где К- показатель степени
Применяется в случае, если каждая варианта
Х встречается в совокупности один или
одинаковое число раз
Χ =
Это
K
Χ
K
∑
Χ
∑
K
⋅ fi
fi
Применяется в случае, если каждая
варианта Х встречается в совокупности
не одинаковое число раз, т.е. по
сгруппированным данным
42.
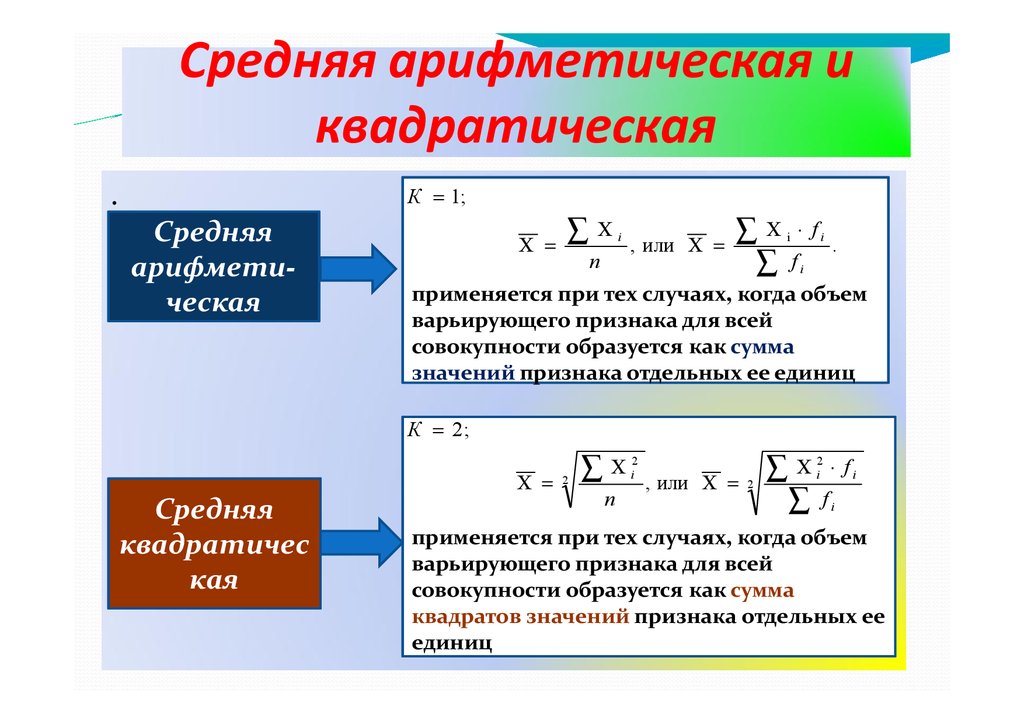
Средняя арифметическая иквадратическая
.
К = 1;
Средняя
арифметическая
Χ =
∑
Χi
n
, или Χ =
∑Χ
∑
i
⋅ fi
fi
.
применяется при тех случаях, когда объем
варьирующего признака для всей
совокупности образуется как сумма
значений признака отдельных ее единиц
К = 2;
Средняя
квадратичес
кая
Χ =
2
∑Χ
n
2
i
, или Χ =
2
∑Χ
∑
2
i
⋅ fi
fi
применяется при тех случаях, когда объем
варьирующего признака для всей
совокупности образуется как сумма
квадратов значений признака отдельных ее
единиц
43.
Мода и медиана— Моду и медиану используют для изучения
внутреннего строения и структуры рядов
распределения значений признака.
Величина признака (варианта), которая
Мода
Медиана
чаще всего встречается в данной совокупности.
В вариационном дискретном ряду модой
выступает варианта, имеющая наибольшую
частоту
Варианта, которая находится в середине
вариационного ряда.
Медиана делит ряд пополам, по обе
стороны от нее (вверх и вниз) находится
одинаковое количество единиц
совокупности
44.
Методика расчёта модыВ интервальных рядах с равными интервалами мода
вычисляется по формуле
Мо = X0 +i (ƒm–ƒm-1)
(ƒm – ƒm-1) + (ƒm – ƒm+1)
— где X0 – минимальная граница модального интервала;
— i – величина модального интервала;
— ƒm – частота модального интервала;
— ƒm-1 – частота интервала, предшествующего
модальному интервалу;
— ƒm+1 – частота интервала, следующего за модальным.
— Модальный интервал в интервальном ряду
определяется по наибольшей частоте
45.
Методика расчёта медианы— В дискретном вариационном ряду определение
медианного значения признака сводится к определению
номера медианной единицы ряда по формуле
Nме= (n+1)/ 2
где n – объем совокупности.
В интервальном ряду с равными интервалами медиана
рассчитывается по формуле
Me=X0+i * (½∑ƒ – Sm-1)
ƒm
— где X0 – начальное значение медианного интервала;
— i– величина медианного интервала;
— ∑ƒ – сумма частот ряда;
— Sm-1 – сумма накопленных частот в интервалах,
предшествующих медианному;
— ƒm – частота медианного интервала.
46.
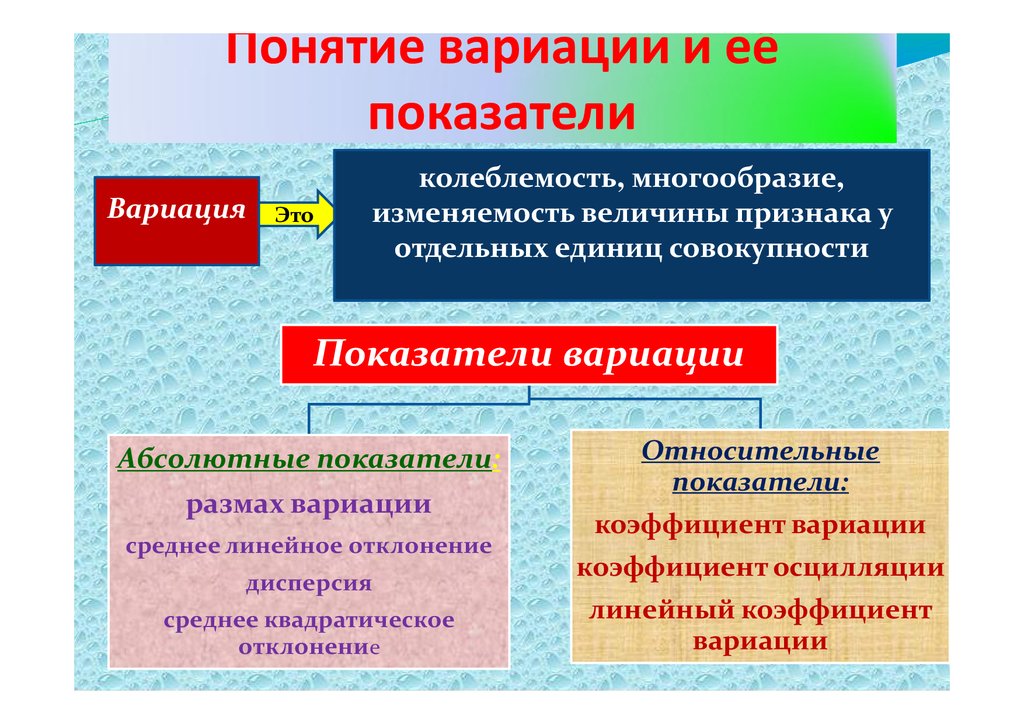
Понятие вариации и еёпоказатели
Вариация
Это
колеблемость, многообразие,
изменяемость величины признака у
отдельных единиц совокупности
Показатели вариации
Абсолютные показатели:
размах вариации
среднее линейное отклонение
дисперсия
среднее квадратическое
отклонение
Относительные
показатели:
коэффициент вариации
коэффициент осцилляции
линейный коэффициент
вариации
47.
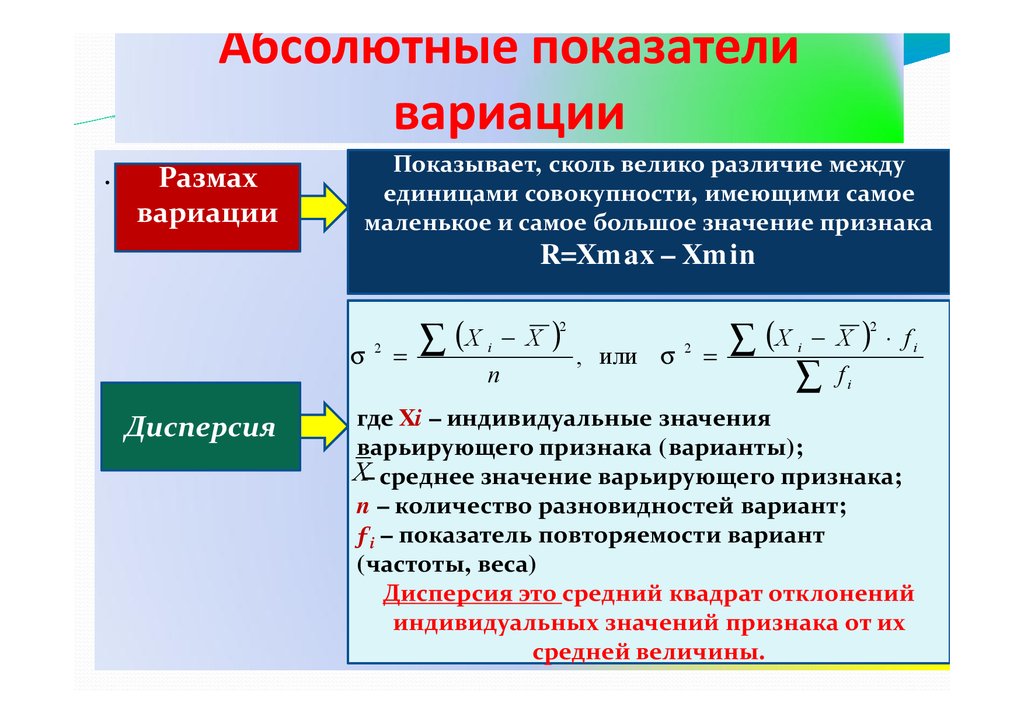
Абсолютные показателивариации
.
Размах
вариации
Показывает, сколь велико различие между
единицами совокупности, имеющими самое
маленькое и самое большое значение признака
R=Xmax – Xmin
σ
Дисперсия
2
=
∑ (X
i
n
− X
)
2
, или σ
2
=
∑ (X
i − X
∑ fi
)
2
⋅ fi
где Xi – индивидуальные значения
варьирующего признака (варианты);
X– среднее значение варьирующего признака;
n – количество разновидностей вариант;
ƒi – показатель повторяемости вариант
(частоты, веса)
Дисперсия это средний квадрат отклонений
индивидуальных значений признака от их
средней величины.
48.
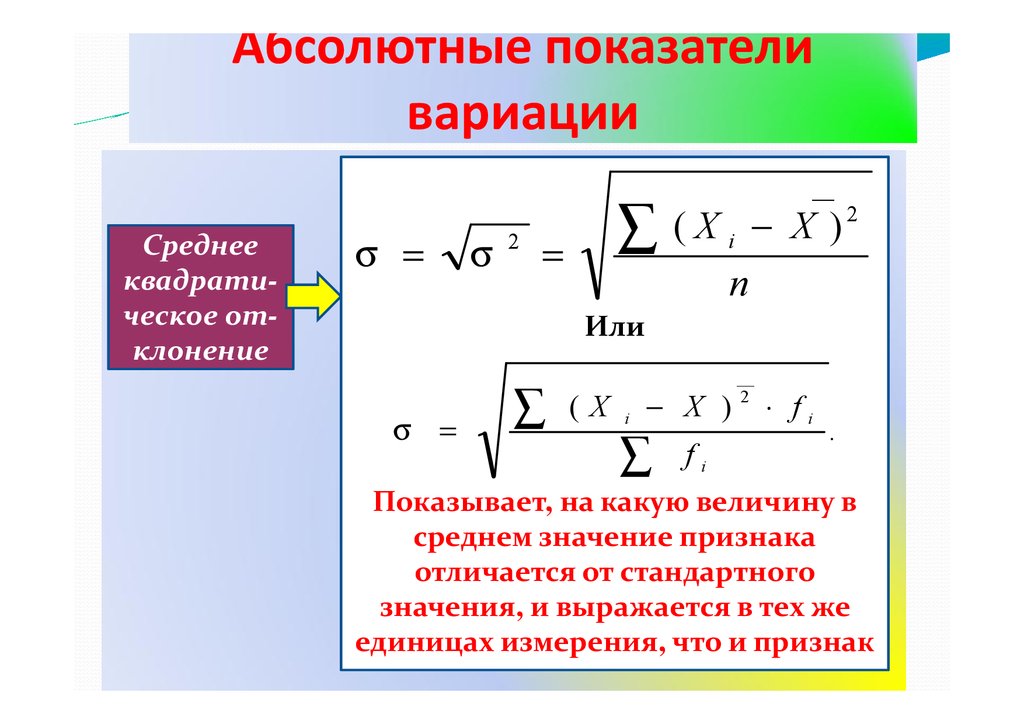
Абсолютные показателивариации
Среднее
квадратическое отклонение
σ =
σ
2
∑
=
__
( X i − X )2
n
Или
σ =
∑
(X
i
− X )
∑
fi
__
2
⋅ fi
.
Показывает, на какую величину в
среднем значение признака
отличается от стандартного
значения, и выражается в тех же
единицах измерения, что и признак
49.
СпасибоЗа внимание !

























 mathematics
mathematics








