matematicheskaya-statistika-v-meditsine

1. Математическая статистика

1

2.

Статистические данные – это сведения о
числе объектов какого - либо множества,
обладающих некоторым признаком
Пример:сведения о числе разводов на число
вступивших в брак.
Математическая статистика изучает
математические методы систематизации,
обработки и использования статистических
данных для научных и производственных
целей
2

3.

Основной метод обработки данных – выборочный
Основа - теория вероятности, в которой
изучаются математические модели реальных
случайных явлений
Математическая статистика связывает реальные
случайные явления и их математические
вероятностные модели
Математическая статистика возникла в 17 веке
одновременно с теорией вероятности
3

4. Статистическое исследование

Сплошное
Исследуется каждый
объект совокупности
Выборочное
Исследуется
отобранные некоторым
образом объекты
4

5.

Генеральная совокупность – совокупность
всех исследуемых объектов
Выборочная совокупность (выборка) –
совокупность случайно отобранных объектов
Случайный отбор – это такой отбор, при
котором все объекты генеральной совокупности
имеют одинаковую вероятность попасть в
выборку
5

6. Выборка

повторная
Объект извлекается из
генеральной совокупности,
исследуется и возвращается
в генеральную
совокупность, берется
следующий, исследуется и
возвращается и т.д.
бесповторная
Объект извлекается из
генеральной совокупности,
исследуется и не
возвращается, берется
следующий и т.д.
6

7.

Объём генеральной совокупности – это число
равное количеству объектов генеральной
совокупности.
Объём выборки – это число равное количеству
объектов выборочной совокупности.
Пример.
Из 10000 упаковок лекарства для контроля
отобрали 100 упаковок
Объем генеральной совокупности равен 10000,
объем выборки – 100
7

8.

Математическая статистика занимается
вопросом: можно ли установив свойство выборки,
считать, что оно присуще всей генеральной
совокупности
Для этого выборка должна быть достаточно
представительной (репрезентативной), т.е.
достаточно полно отражать изучаемое свойство
объектов
Поэтому отбор объектов в выборку
осуществляется случайно, а изучаемому свойству
должна быть присуща статистическая
устойчивость: при многократном повторении
исследования наблюдаемые события повторяются
достаточно часто (статистическая устойчивость
частот)
8

9.

Для статистической обработки результаты
исследования объектов, составляющих выборку,
представляют в виде числовой выборки
(последовательность чисел): x1 , x 2 ,..., x n
Вариационный ряд – это последовательность
элементов выборки, записанная в порядке
неубывания их значений.
Разность между наибольшим значением
числовой выборки и наименьшим называется
размахом выборки
P xmax xmin
9

10.

Рассмотрим числовую выборку объема n, полученную
при исследовании некоторой генеральной совокупности
Значение x1 встречается в выборке n1 раз x2 встречается
n2 раза …….xn встречается nn раз.
Наблюдаемые значения xi называют вариантами, а
последовательность вариант, записанных в
возрастающем порядке, - вариационным рядом.
Числа n1 , n2 ,..., nn называются частотами значений
nn
n1 n2
,
,...,
Отношения частот к объему выборки
n n
n
называются относительными частотами значений
n1 n2 ... nn n
nn
n1 n2
...
1
n n
n
10

11.

Статистическим распределением выборки
называют перечень вариант и соответствующих им
частот:
x1 x2 x3 … xn
n1 n2 n3 … nn
Или относительных частот:
x1
x2
x3
…
n1/n n2/n n3/n …
xn
nn/n
11

12.

Пример.
Для выборки определить объем и размах, найти
статистический ряд и выборочное распределение:
3, 8, -1, 3, 0, 5, 3, -1, 3, 5
Объем: n = 10, размах = 8 – (-1) =9
Статистический ряд:
xi
-1
0
3
5
8
ni
2
1
4
2
1
Выборочное распределение:
xi
-1
0
3
5
8
ni
n
0,2
0,1
0,4
0,2
0,1
(убеждаемся 0,2 + 0,1 + 0,4 + 0,2 + 0,1 = 1)
12

13. Графические изображения выборки

Если выборка задана значениями и их частотами
или статистическим рядом, то строится полигон
Полигон частот
Полигон относительных частот
Это ломаная с вершинами в точках
Это ломаная с вершинами в точках
x1 ; n1 , x2 ; n2 ,..., xn ; nn
nn
n2
n1
x1 ; , x 2 ; ,..., x n ;
n
n
n
13

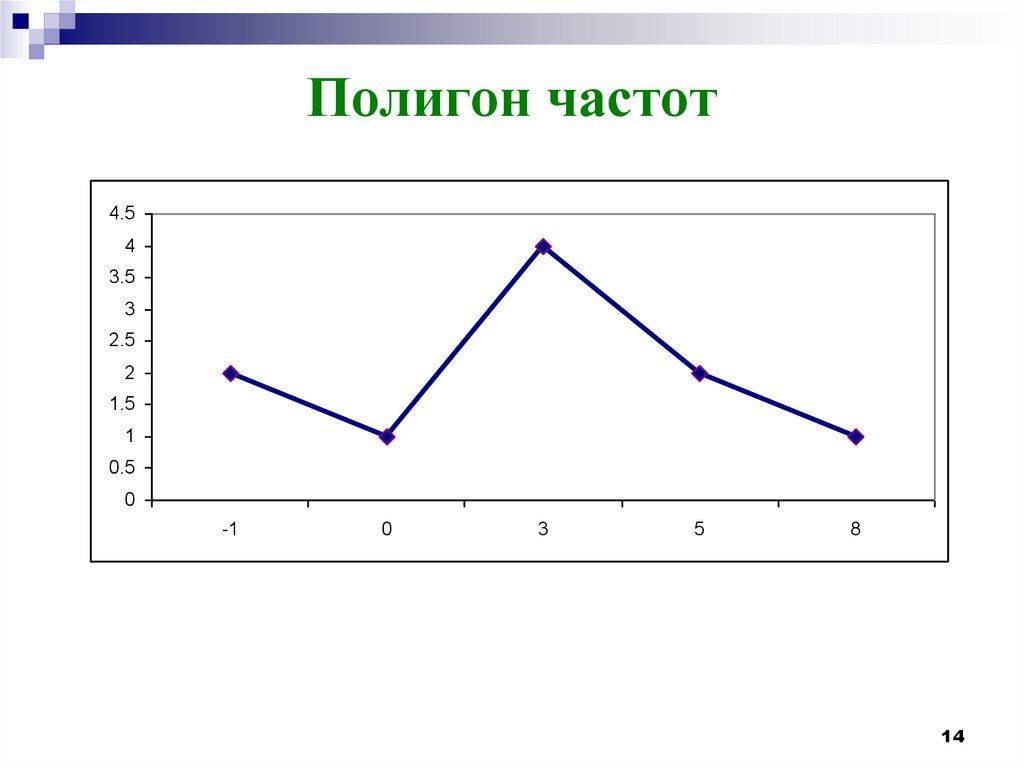
14. Полигон частот

4.5
4
3.5
3
2.5
2
1.5
1
0.5
0
-1
0
3
5
8
14

15.

При большом объеме выборки строится
гистограмма
Гистограмма частот
гистограмма относительных частот
Для построения гистограммы промежуток от наименьшего значения выборки
до наибольшего разбивают на несколько частичных промежутков длины h
Для каждого частичного промежутка подсчитывают сумму частот значений
выборки, попавших в этот промежуток (Si)
Значение выборки, совпавшее с правым концом частичного промежутка
(кроме последнего промежутка), относится к следующему промежутку
Затем на каждом промежутке, как на основании, строим прямоугольник с
высотой S i
h
Ступенчатая фигура, состоящая из таких прямоугольников, называется
гистограммой частот
Площадь такой фигуры равна объёму выборки
15

16.

Гистограммой относительных частот называют
ступенчатую фигуру, состоящую из прямоугольников,
основанием которых являются частичные промежутки
длины h, а высотой отрезки длиной i
h
где i – сумма относительных частот значений выборки,
попавших в i промежуток
Площадь такой фигуры равна 1
16

17.

Пример.
В результате измерения напряжения в электросети
получена выборка. Построить гистограмму частот,
если число частичных промежутков равно 5.
218, 224, 222, 223, 221, 220, 227, 216, 215, 220, 218,
224, 225, 219, 220, 225, 225, 221, 223, 220, 217, 219,
230, 222
n = 24
Наибольшее значение – 230
Наименьшее значение – 215
Размах: 230 – 215 = 15
Длина частичных промежутков: h 15 3
5
17

18.

№
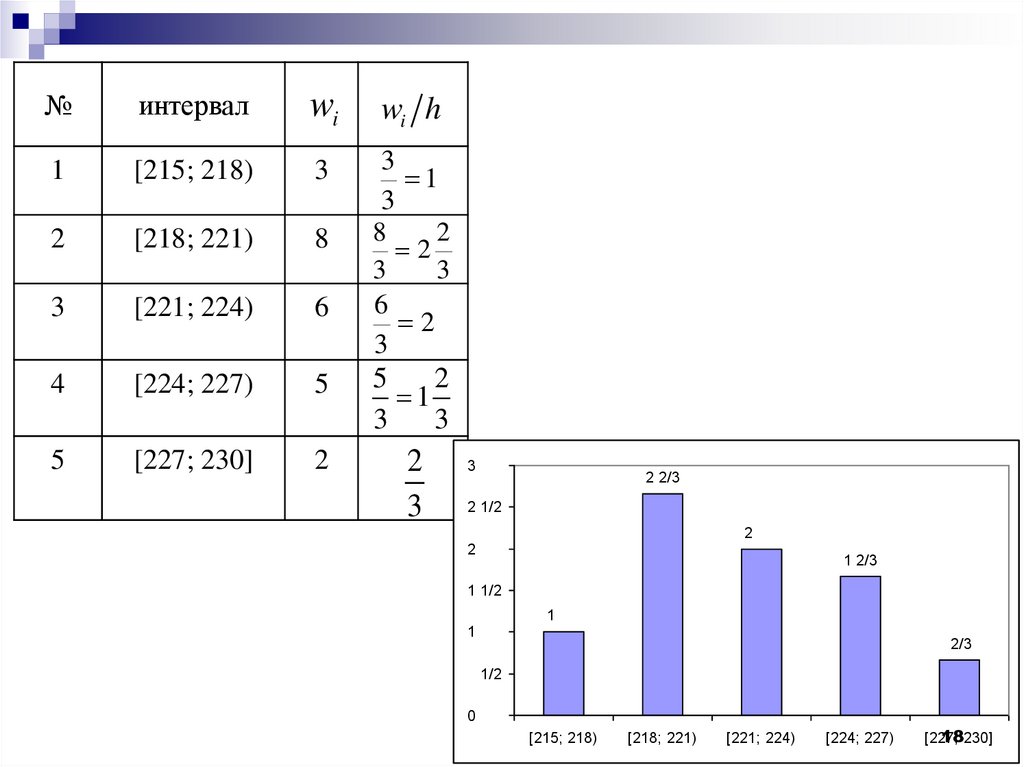
интервал
wi
wi h
1
[215; 218)
3
2
[218; 221)
8
3
[221; 224)
6
4
[224; 227)
5
3
1
3
8
2
2
3
3
6
2
3
5
2
1
3
3
5
[227; 230]
2
2
3
3
2 2/3
2 1/2
2
2
1 2/3
1 1/2
1
1
2/3
1/2
0
[215; 218)
[218; 221)
[221; 224)
[224; 227)
18230]
[227;

19. Выборочные характеристики

Для выборки объема n x1 , x2 ,..., xn
1. Выборочное статистическое ожидание
(выборочное среднее) – это среднее арифметическое
значений выборки
x1 x2 ... xn
x
n
Если выборка задана статистическим рядом, то
n1 x1 n2 x2 ... nn xn
x
n
19

20.

Выборочные характеристики
2. Выборочная дисперсия – это среднее
арифметическое квадратов отклонений значений
выборки от выборочного среднего
x x x x ... x x
S
2
1
2
2
2
0
n
n
Если выборка задана статистическим рядом, то
n1 x1 x n2 x2 x ... nn xn x
S0
n
2
2
3. Среднее квадратическое
(или стандартное) отклонение:
2
S0
20

21.

Выборочные характеристики
Упрощенная формула для дисперсии:
S0 x x
2
2
2
Здесь x - средний квадрат значений признака,
2
x - квадрат среднего.
Пример. Найдем дисперсию по заданному распределению
xi
1
2
3
4
ni
20
15 10 5
x
20 1 15 2 10 3 5 4 100
2
20 15 10 5
50
20 12 15 22 10 32 5 42
x
5
50
2
S0 x 2 x 5 22 1
2
21

22.

Выборочные характеристики
4. Мода – значение варианты, имеющей
наибольшую частоту появления.
Ряд чисел может иметь более одной моды или
не иметь моды совсем
Пример: 35, 35, 36, 36, 36, 36, 37, 37, 38, 39, 39
36 – мода ряда
22

23.

5. Медиана (срединный элемент) - элемент
упорядоченного вариационного ряда, левее и
правее которого имеется одинаковое количество
элементов выборки.
Если в упорядоченном ряду чисел нечётное
число членов, то медиана – это среднее в ряду
число.
Если в упорядоченном ряду чисел чётное число
членов, то медиана – это среднее
арифметическое чисел, записанных посередине.
1) 64, 72, 72, 75, 78, 82, 85, 91, 93
2) 64, 72, 72, 75, 78, 82, 85, 88, 91, 93
(78+82):2=80
23

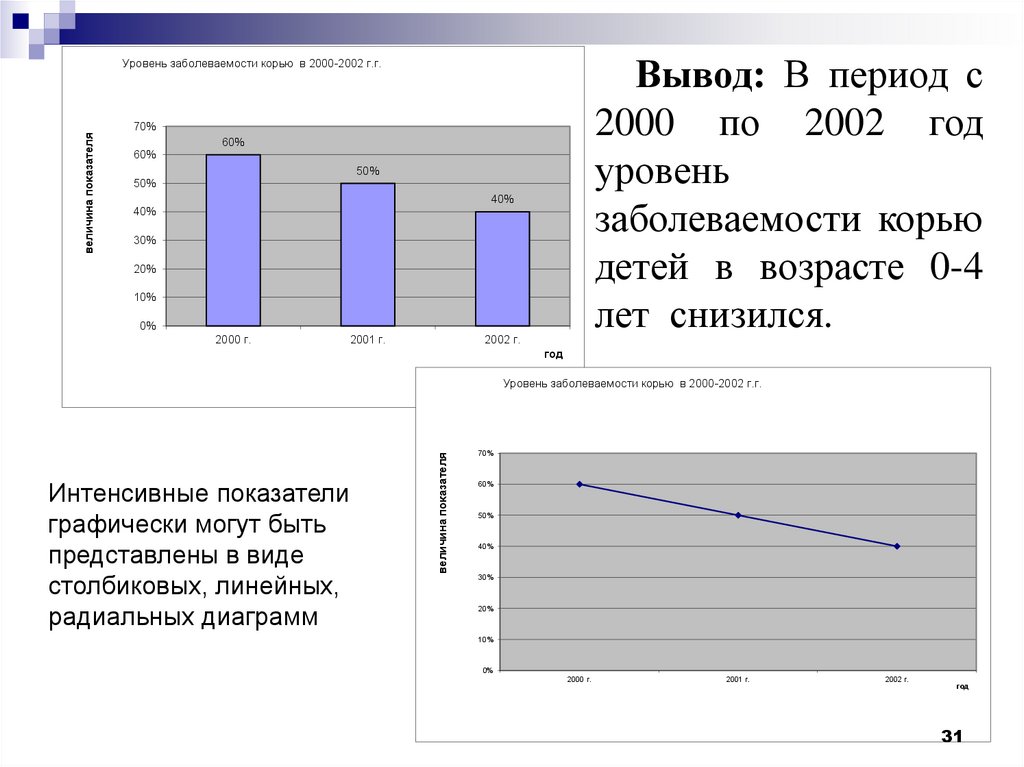
24. Медицинская статистика

24

25.

Медицинская
статистика
определяет
проблемы
современного здравоохранения на основе изучения и анализа
общепринятых статистически показателей, характеризующих:
- здоровье населения – оценка здоровья населения по
совокупности показателей демографических, физического
развития и заболеваемости;
-структуру и реальные возможности здравоохранения – сеть
лечебно-профилактических организаций, их состояние и
оснащенность,
медицинские
кадры
(структура,
профессиональный уровень, повышение квалификации),
медицинские программы и технологии.
На основании анализа статистических данных выстраивают
прогноз – обоснованное суждение о возможном состоянии
объекта в будущем, альтернативных путях и сроках
достижения этих состояний (инновационные программы
развития, инновационные технологии).
25

26.

Точность прогноза определена объемом истинных (верифицированных)
исходных данных, периодом их сбора, методиками и подходами
прогнозирования.
Традиционная статистическая система в здравоохранении основана на
получении данных в виде отчетов. Система отчетов имеет единую
номенклатуру, единые показатели объема работы и использования ресурсов,
обеспечивающих сравнимость данных.
Анализ и обобщение ситуации осуществляют не только на основании
данных отчетов, но и путем проводимых выборочных статистических
исследований.
Статистическое исследование включает три основных этапа.
- Статистическое наблюдение – формирование первичных статистических
данных.
- Сводка и группировка данных – первичные статистические данные
делят по признакам различия и объединяют по признакам сходства.
Подсчитывают суммарные показатели по группам и в целом. Изучаемые
явления, в зависимости от существенных признаков, подразделяют на типы,
группы и подгруппы.
Обработка
и
анализ
полученных
данных,
обнаружение
закономерностей. Рассчитывают относительные и средние величины,
показатели, характеризующие наличие связей между признаками случаев,
обосновывают динамику явлений. Цифровой материал представляют в виде
26
таблиц и графиков.

27. Типы относительных величин

МЕДИЦИНСКАЯ СТАТИСТИКА
Типы относительных величин
Интенсивные показатели
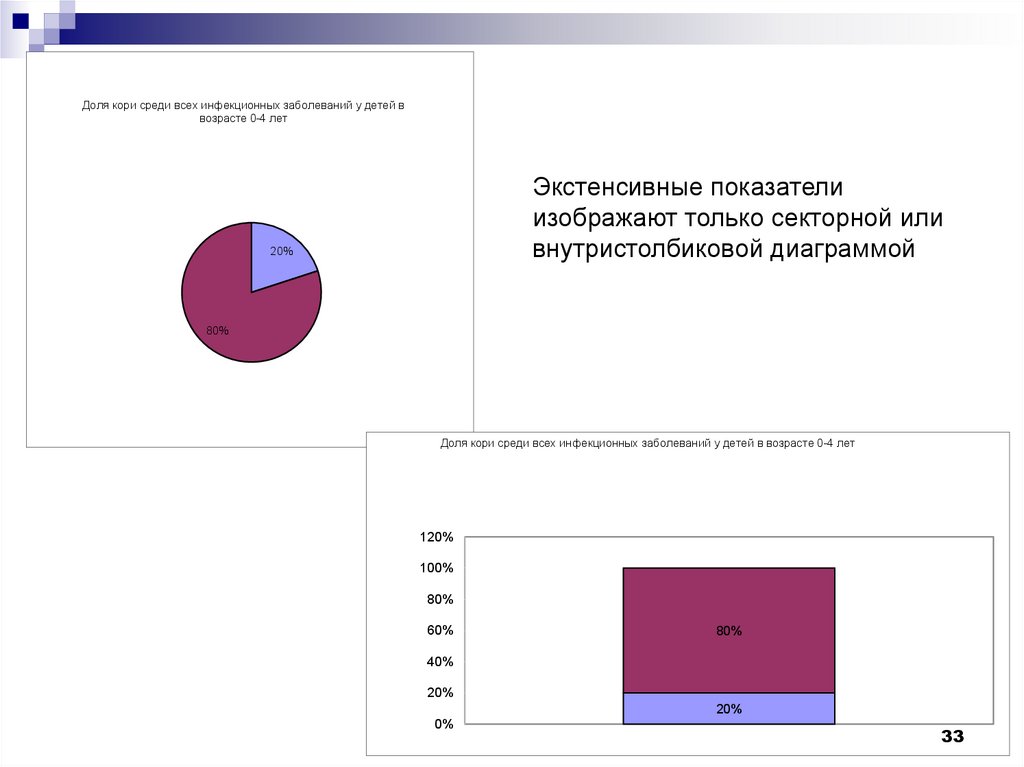
Экстенсивные показатели
Показатели соотношения
Показатели наглядности
27

28.

Интенсивный показатель (показатель частоты)
определяет интенсивность развития (частоту,
уровень, распространенность) явления во
взаимосвязанной с ним среде, которая
продуцирует это явление.
явление
Интенсивный показатель =
∙ 10