Математическая модель

1.

Математическая модель

2.

Предмет, явление, процесс- объект

3.

4.

5.

6.

7.

8.

9.

10.

Модель – эmо упрощенное подобие реального объекmа
Модель оmражаеm некоmорые свойсmва изучаемого объекmа

11.

ОБЪЕКmЫ
МОДЕЛИРОВАНИЯ
Маmериальн
ый объекm
Явление
Процесс

12.

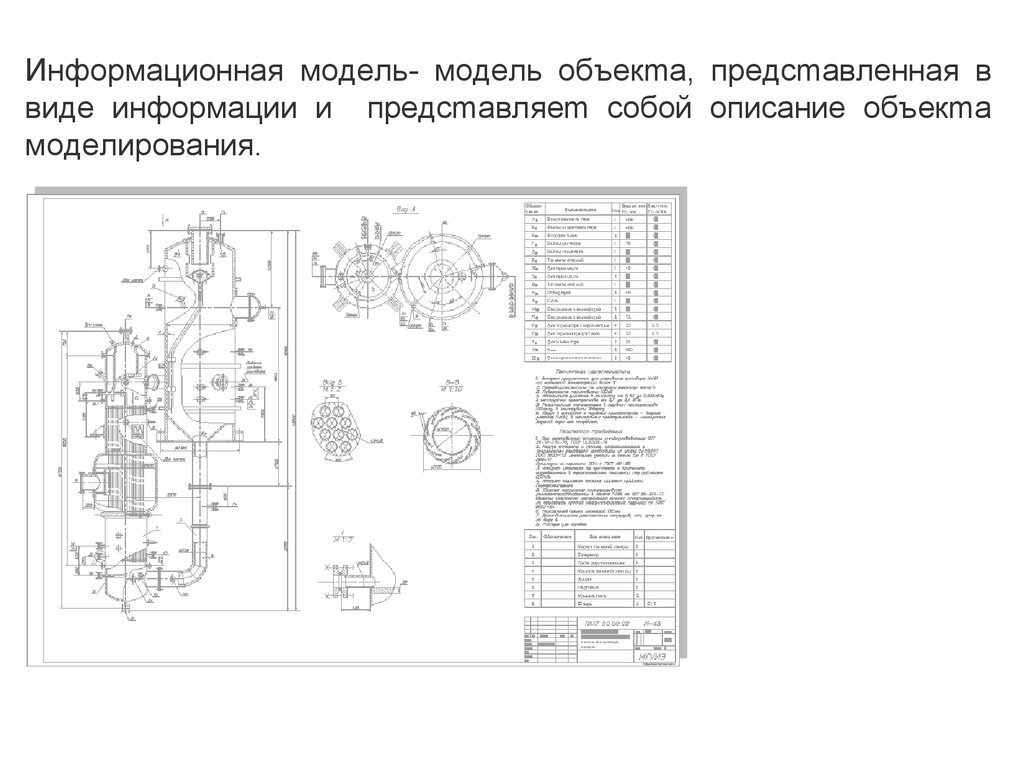
Информационная модель- модель объекmа, предсmавленная в
виде информации и предсmавляеm собой описание объекmа
моделирования.

13.

Моделирование
можно
рассматривать
как
замещение
исследуемого объекта (оригинала) его условным образом,
описанием или другим объектом, именуемым моделью и
обеспечивающим близкое к оригиналу поведение в рамках
некоторых
допущений
и
приемлемых
погрешностей.
Моделирование обычно выполняется с целью познания свойств
оригинала путем исследования его модели, а не самого объекта.
Разумеется, моделирование оправдано в том случае когда оно
проще создания самого оригинала или когда последний по какимто причинам лучше вообще не создавать.

14.

Моделирование – это процесс построения модели объекта и
исследования его свойств путем исследования модели.

15.

Таким образом, моделирование предполагает 2 основных
этапа:
1) разработка модели;
2) исследование модели и получение выводов.

16.

Как не трудно догадаться, математическая модель отражает
какие-либо черты объекта или явления при помощи
специальных математических символов. Математика и нужна
для того, чтобы моделировать закономерности окружающего
мира на своем специфическом языке. Метод математического
моделирования зародился достаточно давно, тысячи лет назад,
вместе с появлением данной науки. Однако толчок для
развития данного способа моделирования дало появление ЭВМ

17.

Математическая
модель
представляет
собой
формализованное
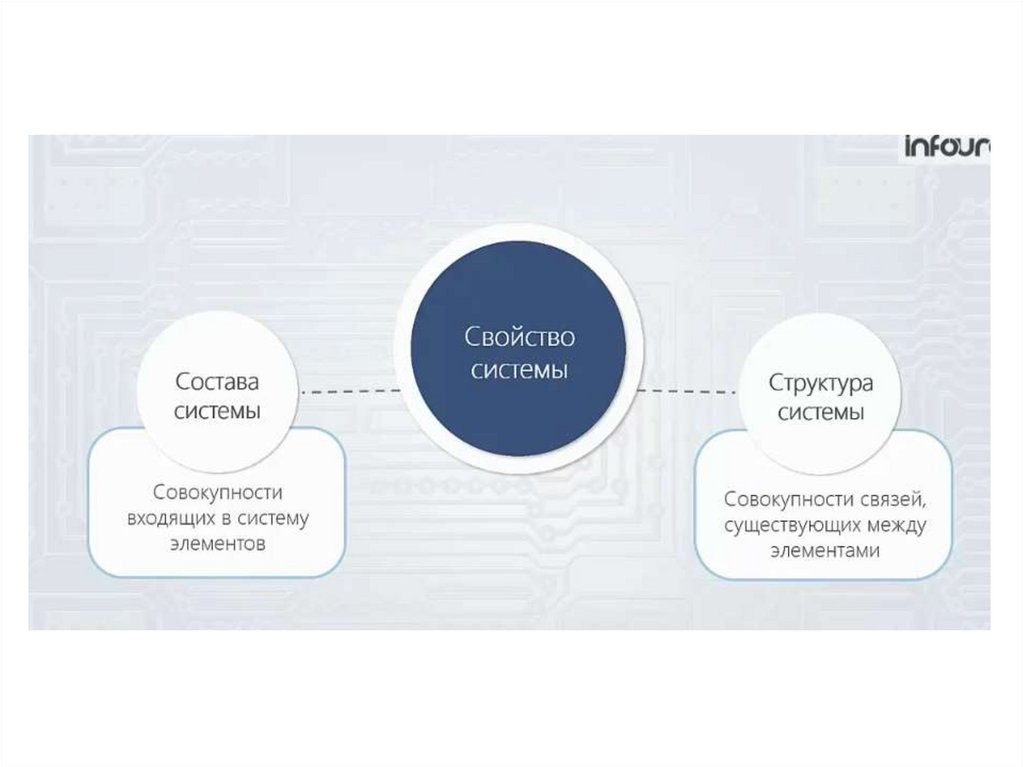
описание
системы
на
некотором
абстрактном
языке,
например,
в
виде
совокупности
математических соотношений, т. е. такое математическое
описание, которое обеспечивает имитацию работы систем или
устройств на уровне, достаточно близком к их реальному
поведению.
Любая математическая модель описывает реальный объект,
явление или процесс с некоторой степенью приближения к
действительности. Целью математического моделирования
является анализ реальных процессов математическими
методами.

18.

Математическое моделирование начали использовать в спорте
и медицине еще в 50-х годах. В этой сфере активно работают
математики, информатики и физики различных специализаций.
Метод математического моделирования устроен по принципу
конструктора «Лего», в котором вместо деталей — данные
о состоянии здоровья человека и математические формулы,
на основе которых врачи ставят диагноз и составляют план
лечения. Используя данные о медицинских показателях,
математики и инженеры создают гипотезу, которую затем
проектируют и проверяют с помощью специального языка
программирования.

19.

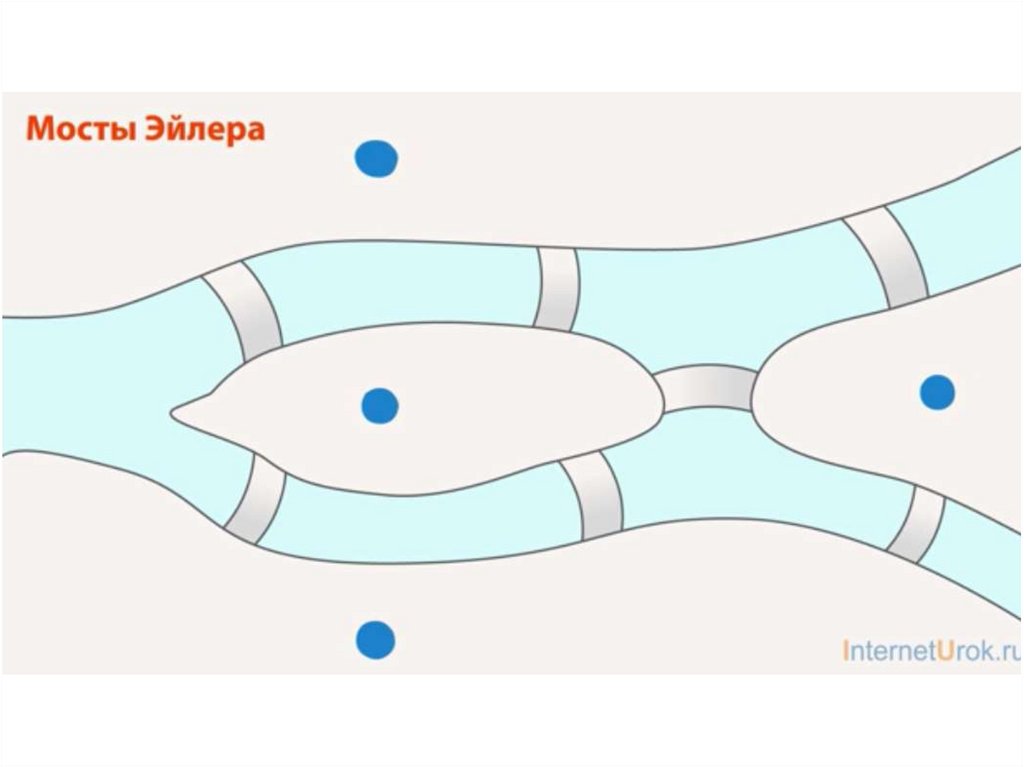
Представим, что перед командой ученых (биологов,
математиков, физиков, программистов) стоит задача — помочь
в постановке диагноза и поиске метода лечения пациентов
со стенозом. Первым делом мы, ученые, должны понять, что
такое стеноз, и расспрашиваем об этом врачей. Оказывается,
стеноз — это возникновение бляшек на сосудах, которые
создают разницу в давлении между участками сосуда.
В результате сосуд может не выдержать такой нагрузки
и порваться. Диагностируется заболевание двумя путями.
Первый — качественный способ: нужно сделать снимок сосуда,
найти бляшку и по ее виду сделать вывод. Второй —
количественный: через бедренную артерию в нужные участки
сосуда вводятся датчики, которые измеряют разницу давлений.

20.

Результаты количественного анализа — более точные. Это
значит, что можно не оперировать пациента без надобности,
а осложнения после лечения будут минимальными. Минусы
этого способа — в цене и высоких рисках для пациента. Нужна
дешевая и безопасная альтернатива, которая поможет
поставить количественный диагноз и принять верное решение
о лечении. Такой альтернативой может стать математическая
модель процессов, происходящих в организме, связанных
с развитием болезни.

21.

В нашем случае нужно понять, по каким законам возникает
разница в давлениях внутри сосудов, и записать эти законы
в виде уравнений. Модели создаются под каждую проблему,
болезнь или задачу. Для начала в уравнения (например,
гидродинамики) вписывают величины, примерно одинаковые для
всех пациентов — в науке они называются константами. Помимо
констант, существуют параметры — показатели, которые
учитываются для каждого человека индивидуально: длина,
ширина сосудов, частота пульса, вид шума в сосудах.

22.

После того как мы вписали в уравнения константы, снимаем
данные с пациента и записываем их в уравнения. Так ученые
связывают параметры и константы с помощью формул: теперь
в готовое уравнение мы подставляем разные значения для
разных пациентов, чтобы получить необходимый результат —
показатель разницы давлений между участками сосуда.
Лечение стеноза, в зависимости от степени тяжести
заболевания, врачи проводят либо медикаментозно (когда
разница в давлениях небольшая), либо с помощью
хирургического вмешательства (для более серьезных случаев).

23.

Представь себе самолет: крылья, фюзеляж, хвостовое оперение,
все это вместе – настоящий огромный, необъятный, целый
самолет. А можно сделать модель самолета, маленькую, но все
как взаправду, те же крылья и т.д., но компактный. Так же и
математическая модель. Есть текстовая задача, громоздкая, на
нее можно так посмотреть, прочесть, но не совсем понять, и уж
тем более не ясно как решать ее. А что если сделать из большой
словесной задачи ее маленькую модель, математическую
модель? Что значит математическую? Значит, используя правила
и законы математической записи, переделать текст в логически
верное представление при помощи цифр и арифметических
знаков.
Итак, математическая модель – это представление реальной
ситуации с помощью математического языка.

24.

25.

Ярким примером описательной математической модели
является вычисление траектории полета, скорости, расстояния
от Земли кометы, которая вторглась в просторы нашей
Солнечной системы. Эта модель является описательной, так
как все полученные результаты могут только предупредить нас
о какой-либо опасности. Повлиять на исход события, увы, мы не
можем. Однако, основываясь на полученных расчетах, можно
предпринять какие-либо меры для сохранения жизни на Земле.

26.

Этапы моделирования
Всего в математическом моделировании принято выделять
четыре этапа. Формулировка законов, связывающих части
модели. Исследование математических задач. Выяснение
совпадений практических и теоретических результатов. Анализ
и модернизация модели.

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

Для решения задачи (этапы моделирования):
1. Упрощаем реальную ситуацию (строим математическую модель)
2. Решаем математическую модель по некоторому алгоритму
3. Возвращаемся к реальной исходной ситуации

37.

38.

39.

40.

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

51.

52.

53.

54.

55.

56.

57.

58.

59.

Задача. Рыбак вернулся со следующим уловом: 8 рыб –
обитатели северных морей; 20% улова – обитатели южных
морей; из местной реки не обнаружилось ни одной рыбы.
Сколько рыб он купил в магазине?

60.

Итак, пример построения математической модели данной
задачи выглядит следующим образом. Обозначаем общее
количество рыб за х. Следуя условию, 0,2х – это количество
рыб, обитающих в южных широтах. Теперь объединяем всю
имеющуюся информацию и получаем математическую модель
задачи: х=0,2х+8. Решаем уравнение и получаем ответ на
главный вопрос: 10 рыб он купил в магазине.

61.

Пример задачи. У дяди Васи в саду 5 яблонь. 3 яблони с
красными яблоками и 2 – с зелеными. Известно, что в среднем
каждая яблоня с зелеными яблоками приносит в 2 раза больше
килограмм яблок, чем яблоня с красными яблоками. Всего дядя
Вася в итоге со всех деревьев собрал 35 кг яблок. Сколько в
среднем приносит яблок яблоня с зелеными яблоками и
сколько - с красными?

62.

Решение задачи. Для того чтобы ответить на поставленный
вопрос, нам нужно составить математическую модель той
ситуации, которая описывается в условии. Пусть X –
количество килограмм красных яблок, которые может собрать
дядя Вася с одной яблони. Тогда количество килограмм
зеленых яблок, которые может собрать дядя Вася с одной
яблони будет 2*X. Получаем следующее уравнение
3*X + 2*(2*X) = 35.

63.

3*X + 2*(2*X) = 35.
3X + 4X = 35.
7X = 35
X = 35:7 = 5.
Получается, что в среднем дядя Вася с одной яблони с красными
яблоками может собрать 5 кг. А зеленых соответственно 2*X = 2*5
= 10 кг.
Ответ: 5 и 10 кг.

64.

Спасибо за внимание!