Математические модели

1.

Математические модели

2.

Алгебраические
модели

3.

Формальные модели на языке
алгебры:
Решение уравнений – выполнение
равносильных преобразований выражений,
которые позволяют выразить неизвестную
величину с помощью формулы.
ax bx c 0
2
D b 4ac
2
x1, 2
b D
2a
cos x b
x arccos b 2 n

4.

Постановка задачи:
Дано: уравнение x2 = 8 - х
Найти: корни уравнения
графический
Способ решения

5.

Графическая модель
х 2,3
х - 3,3

6.

Постановка задачи:
Дано: уравнение x3 + 5 = 0
Найти: корни уравнения
Способ решения подбором

7.

Числовая модель
«Половинное деление»
Построим график функции y= x3+5 и на оси Ох возьмем интервал,
содержащий точку пересечения графика функции с осью Ох
С=(А+В)/2
y (В) > 0
y (C) > 0
y (A) < 0
С=В
А
С
В

8.

Числовая модель
«Половинное деление»
С=(А+В)/2
y (В) > 0
y (C) < 0
А
y (A) < 0
С
A
В
С=A
Пока
B A
E
2
A B
x
2
корни определяются с заданной точностью Е

9.

Составим алгоритм решения
1. Вводим данные: А, В, Е
2. Пока B A E
делать: 2
3. С=(А+В)/2
4. Если у(A) * у(C) < 0 то B=C
иначе A=C
5. Конец ветвления
6. Конец цикла
7. X=(A+B)/2

10.

Геометрические модели
(планиметрия)

11.

Информационная модель
графического объекта
Объект
Рисунок или
фрагмент
рисунка
Параметры
Действия
Размеры,
пропорции,
цвет,
форма
Перемещение,
тиражирование,
редактирование,
поворот, отражение,
изменение размеров и
пропорций

12.

Для построения компьютерных моделей
необходимо решить задачи:
Моделирование геометрических
операций, обеспечивающих точные
построения в графическом редакторе;
Моделирование геометрических
объектов с заданными свойствами, в
частности, формой и размерами.

13.

I этап: Постановка задачи
ЦЕЛЬ МОДЕЛИРОВАНИЯ
При отсутствии специальных инструментов
(линейки, транспортира, циркуля)
смоделировать основные геометрические
операции.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Исходные геометрические объекты (отрезок,
радиус, угол) задаются в левом верхнем углу
рабочего поля. Для построений
используются их копии. Построение
основывается на законах геометрии.

14.

II этап: Разработка модели
МОДЕЛЬ 1. Деление отрезков (моделирование функций линейки)
Алгоритм деления отрезка пополам
a
a
1/2a
Построение основано на том, что высота в
равнобедренном треугольнике является
одновременно биссектрисой и медианой. Для
построения достаточно инструмента Линия и
клавиши Shift

15.

МОДЕЛЬ 1. Деление отрезков (моделирование функций линейки)
Алгоритм деления отрезка на n равных частей (для n=3)
x
x
x
x
Для выполнения операции деления используется
отрезок произвольной длины х. Построение основано
на подобии треугольников. Параллельность линий
достигается копированием.

16.

МОДЕЛЬ 2. Построение окружности заданного радиуса и
определение ее центра (моделирование функций циркуля)
Алгоритм построения окружности с заданным радиусом.
a
a
a
Окружность в графическом редакторе вписывается в
квадрат со стороной, равной удвоенному радиусу.

17.

МОДЕЛЬ 2.Деление угла пополам (моделирование функции транспортира).
Алгоритм деления угла пополам.
А
А
К
β
β
О
В C
β/2
О
В
В качестве дополнительного построения используется окружность любого
радиуса. В ее центр помещается копия угла, подлежащего делению. Углы
АОВ и АСВ относятся как 2:1 (докажите это). Отсюда, если линия КО
параллельна линии АС, то она является биссектрисой заданного угла.
Построение сводится к копированию части отрезка АС и установке его копии
к точке О. Полученная параллельная линия КО разделит заданный угол
пополам.

18.

III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
1. Тестирование построенной по заданному
алгоритму модели 1 совмещением отрезков,
полученных при делении.
2. Тестирование построенной по заданному
алгоритму модели 2 совмещением исходного и
повернутого на 90° отрезка с радиусами
полученной окружности.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
Докажите правильность алгоритмов построения.

19.

IV этап. Анализ результатов
Если результаты тестирования
отрицательные, увеличить точность
выполнения алгоритма за счет работы в
увеличенном масштабе (под лупой).

20.

Моделирование объектов с заданными
геометрическими свойствами.
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Задачи на построение возникли в глубокой
древности и были связаны с практическими
потребностями. Можно добиться точности, даже
если под рукой нет специальных измерительных
инструментов, а есть подсобные предметы: кусок
веревки, ровная палочка
Поэтому необходимо научиться строить модели
геометрических фигур с заданными свойствами:
равносторонний треугольник, шестиугольник,
равнобедренный треугольник и пр. Это можно
сделать, используя законы геометрии.

21.

ЦЕЛЬ МОДЕЛИРОВАНИЯ
В среде графического редактора научиться
моделировать геометрические объекты с
заданными свойствами.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Геометрическая фигура характеризуется длиной
сторон и углами, которые необходимо задать в
виде отрезков и углов на рабочем поле
графического редактора перед началом
построения.

22.

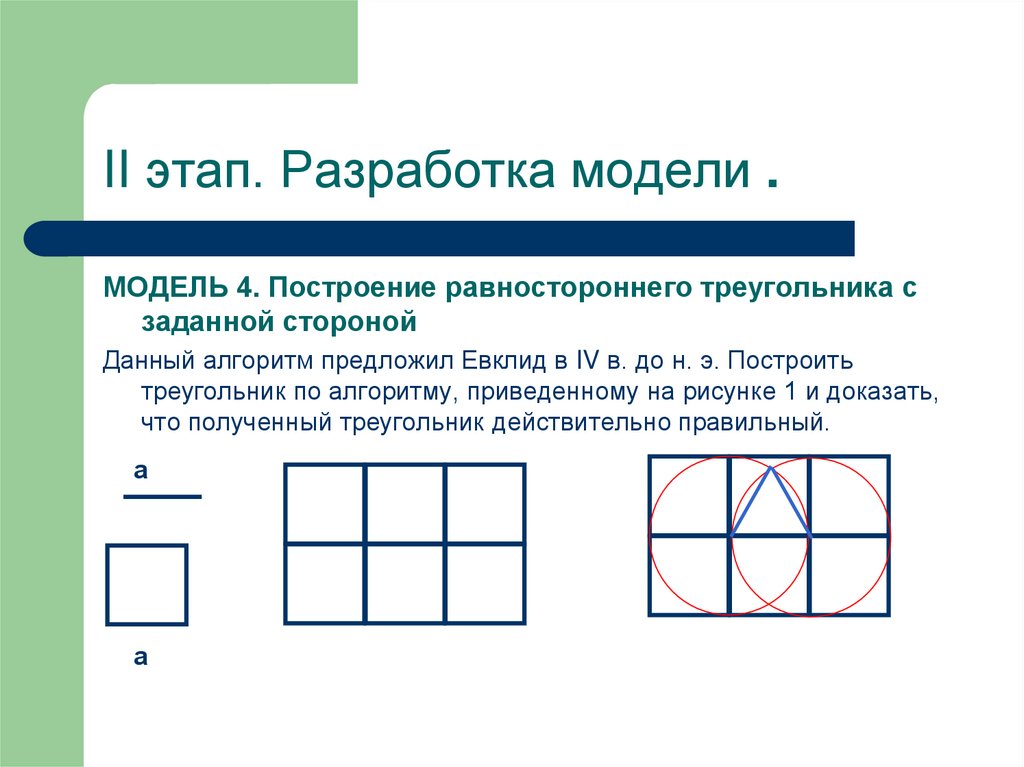
II этап. Разработка модели .
МОДЕЛЬ 4. Построение равностороннего треугольника с
заданной стороной
Данный алгоритм предложил Евклид в IV в. до н. э. Построить
треугольник по алгоритму, приведенному на рисунке 1 и доказать,
что полученный треугольник действительно правильный.
а
а

23.

МОДЕЛЬ 5. Построение правильного шестиугольника с
заданной стороной
а
Используя свойство правильных фигур вписываться в
окружность и то, что сторона равностороннего
шестиугольника равна радиусу описанной окружности,
выполнить построение по алгоритму на рисунке. Начать
построение окружности с радиусом, равным заданной
стороне шестиугольника.
а
а
а
а

24.

III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
1.
Тестирование построенной по заданному алгоритму
модели совмещением с исходными отрезками и углами.
2.
Построение и тестирование модели по собственному
алгоритму с теми же исходными данными.
3. Исследование и анализ двух алгоритмов построения с
целью определения наилучшего.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Докажите правильность приведенного и собственного
алгоритмов для каждой модели.
2. Совместите построения, выполненные по разным
алгоритмам.

25.

IV этап. Анализ результатов
Если при совмещении фигуры не совпали,
то изменить алгоритм построения или
увеличить точность выполнения
алгоритма за счет работы в увеличенном
масштабе (под лупой). Если совпали, то
выберите наиболее удобный алгоритм.

26.

Геометрические модели
(стереометрия)

27.

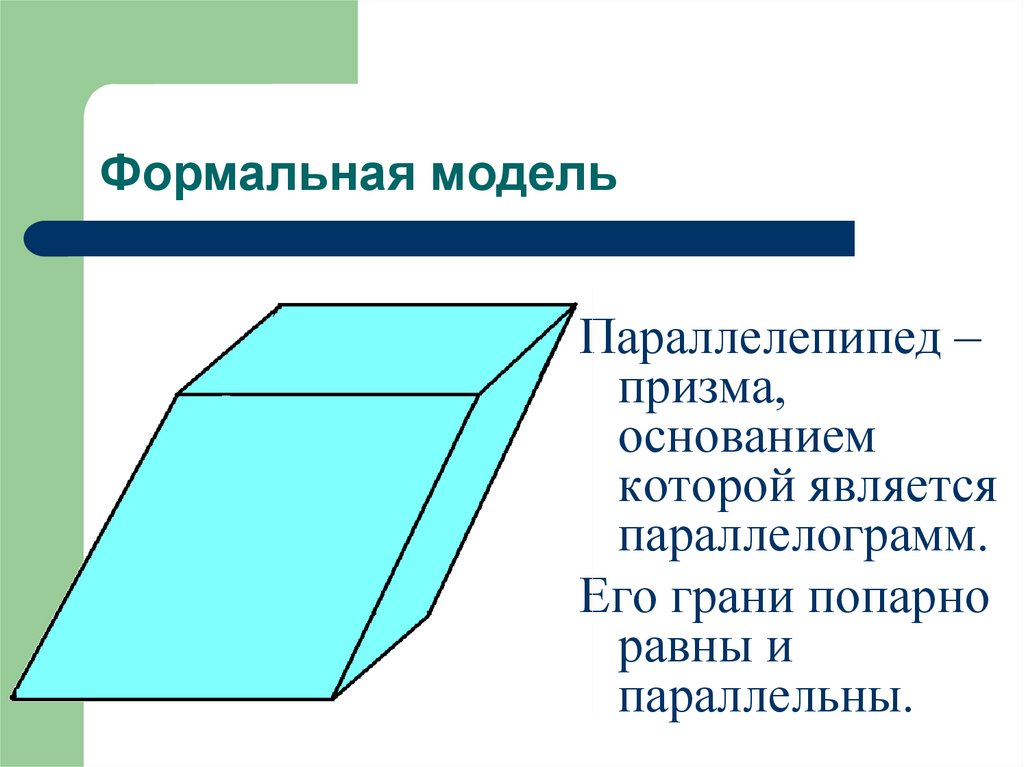
Формальная модель
Параллелепипед –
призма,
основанием
которой является
параллелограмм.
Его грани попарно
равны и
параллельны.

28.

A
D
B
C
К
H
F
М
Прямоугольный параллелепипед –
параллелепипед, все грани которого
прямоугольники. Прямоугольный
параллелепипед с равными ребрами – куб.

29.

A
D
B
C
К
H
Назовите измерения параллелепипеда.
Как найти диагональ?
HB2 = HD2 + HM2 + HK2
Как найти объем?
V = HD * HM * HK
F
М