Представление случайного эксперимента в виде дерева

1.

8 класс
вероятность
и статистика

2.

§ 56
ПРЕДСТАВЛЕНИЕ
СЛУЧАЙНОГО
ЭКСПЕРИМЕНТА В ВИДЕ
ДЕРЕВА

3.

ВВЕДЕНИЕ
Рассмотрим ещё один инструмент
для решения задач на нахождение
вероятности — дерево случайного
опыта. Наряду с диаграммами Эйлера
дерево позволяет наглядно представить
условия данного опыта. Дерево —
разновидность графа. Вспомним его
определение.

4.

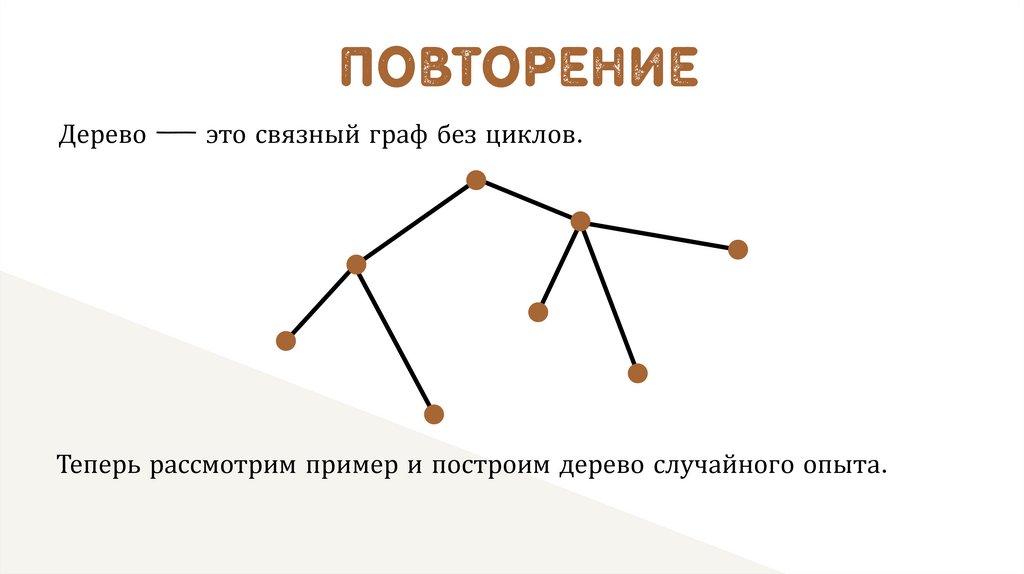
ПОВТОРЕНИЕ
Дерево — это связный граф без циклов.
Теперь рассмотрим пример и построим дерево случайного опыта.

5.

изучение нового материала
Пример:
стрелок стреляет по мишени и с
вероятностью 0,8 может попасть в
мишень. Найди вероятность того,
что стрелок попал при первом
выстреле,
а
при
втором
промахнулся.

6.

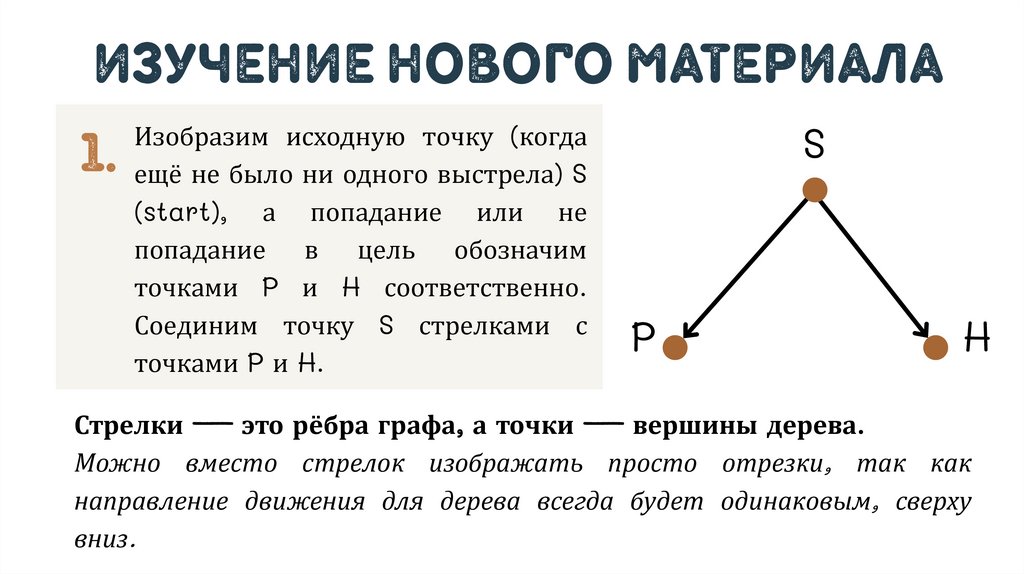
изучение нового материала
1.
Изобразим исходную точку (когда
ещё не было ни одного выстрела) S
(start), а попадание или не
попадание в цель обозначим
точками P и H соответственно.
Соединим точку S стрелками с
точками P и H.
S
P
H
Стрелки — это рёбра графа, а точки — вершины дерева.
Можно вместо стрелок изображать просто отрезки, так как
направление движения для дерева всегда будет одинаковым, сверху
вниз.

7.

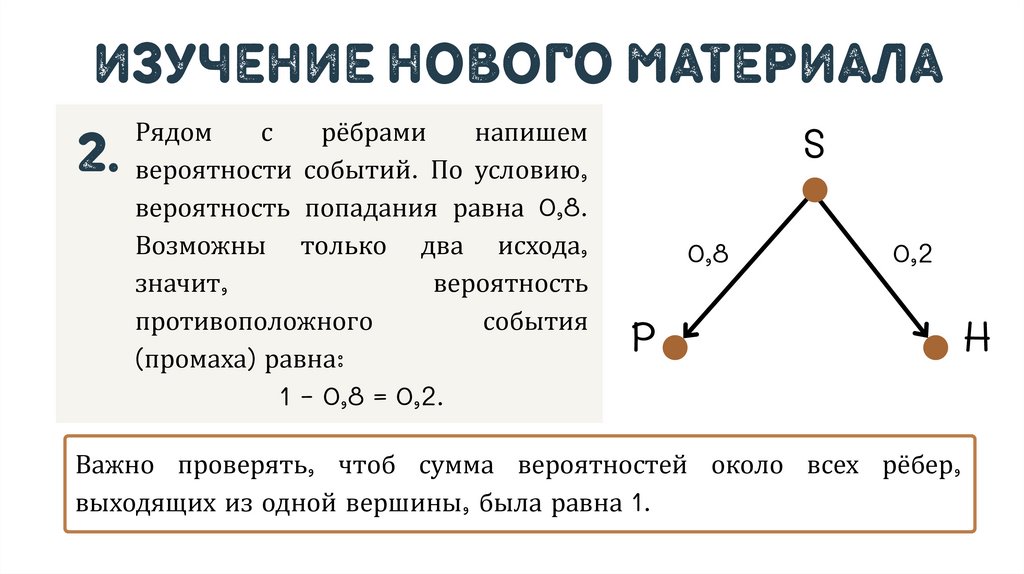
изучение нового материала
2.
Рядом
с
рёбрами
напишем
вероятности событий. По условию,
вероятность попадания равна 0,8.
Возможны только два исхода,
значит,
вероятность
противоположного
события
(промаха) равна:
1 − 0,8 = 0,2.
S
0,8
0,2
P
Важно проверять, чтоб сумма вероятностей около всех рёбер,
выходящих из одной вершины, была равна 1.
H

8.

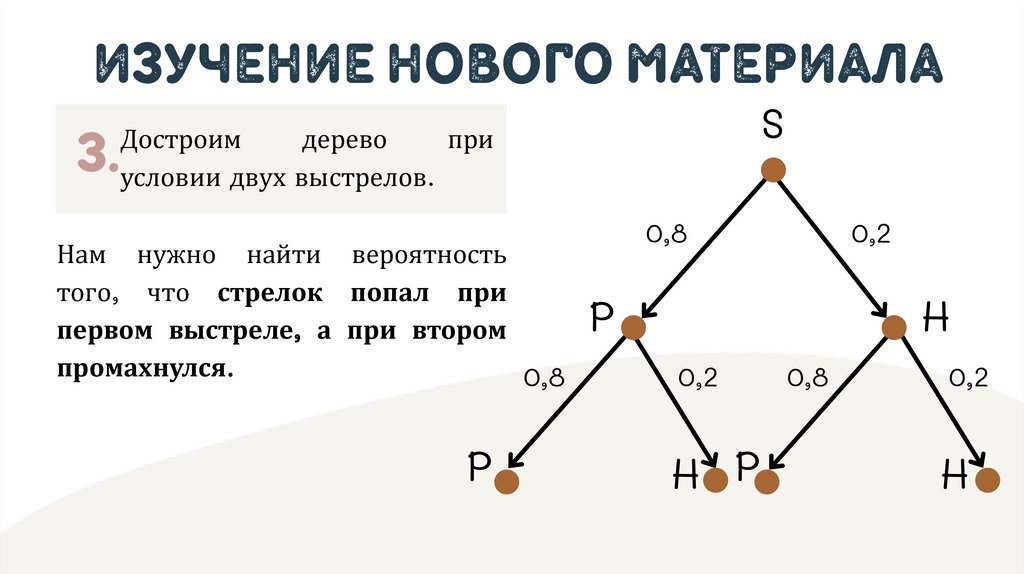
изучение нового материала
3.
S
Достроим
дерево
при
условии двух выстрелов.
Нам нужно найти вероятность
того, что стрелок попал при
первом выстреле, а при втором
промахнулся.
0,8
P
0,8
0,2
P
H
0,2
H P
0,8
0,2
H

9.

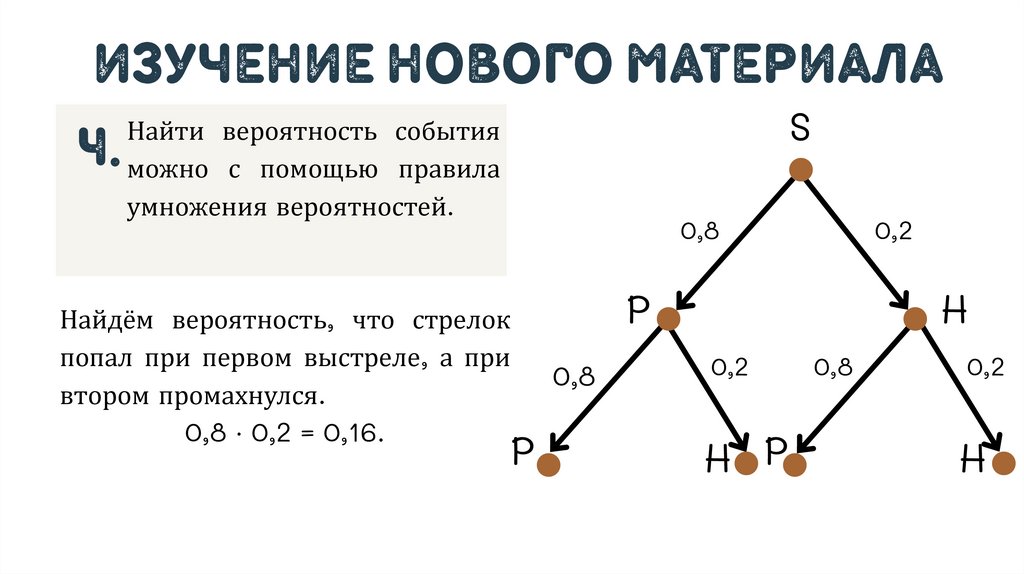
изучение нового материала
Найти вероятность события
S
4. можно с помощью правила
умножения вероятностей.
Найдём вероятность, что стрелок
попал при первом выстреле, а при
втором промахнулся.
0,8 ⋅ 0,2 = 0,16.
0,8
0,2
P
0,8
P
H
0,2
H P
0,8
0,2
H

10.

правило
Чтобы найти вероятность события с
помощью дерева случайного опыта,
нужно найти произведение вероятностей
вдоль цепочки, идущей от начальной
вершины к вершине, изображающей
нужное элементарное событие.

11.

изучение нового материала
S
А если нам нужно узнать
вероятность события «стрелок
один раз попал и один раз
промахнулся
при
двух
выстрелах»?
0,8
0,2
P
0,8
P
H
0,2
H P
0,8
0,2
H

12.

изучение нового материала
S
В этом случае нам подойдут
две цепочки: попал первый раз,
второй
раз
промахнулся
и
промахнулся первый раз, второй
раз попал.
Тут действует правило сложения
вероятностей.
Найдём эту вероятность.
0,8 ⋅ 0,2 + 0,2 ⋅ 0,8 = 0,32.
0,8
0,2
P
0,8
P
H
0,2
H P
0,8
0,2
H

13.

правило
Чтобы найти вероятность события с
помощью дерева случайного опыта,
нужно
сложить
вероятности
всех
цепочек, ведущих к этому событию от
начальной вершины.

14.

закрепление изученного
материала
S
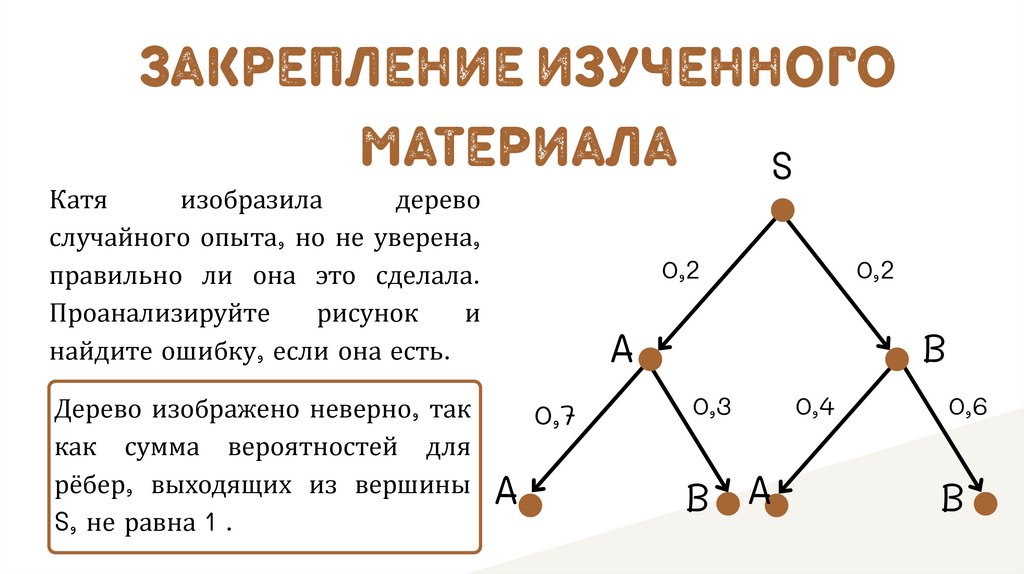
Катя
изобразила
дерево
случайного опыта, но не уверена,
правильно ли она это сделала.
Проанализируйте
рисунок
и
найдите ошибку, если она есть.
Дерево изображено неверно, так
как сумма вероятностей для
рёбер, выходящих из вершины
S, не равна 1 .
0,2
0,2
A
0,7
A
B
0,3
B A
0,4
0,6
B

15.

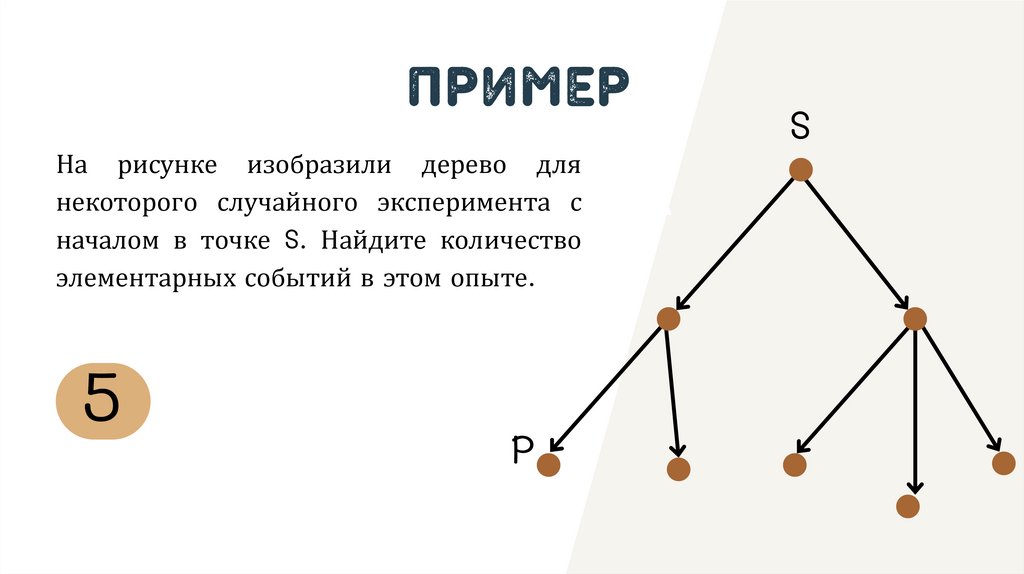
Пример
На рисунке изобразили дерево для
некоторого случайного эксперимента с
началом в точке S. Найдите количество
элементарных событий в этом опыте.
5
P
S
A

16.

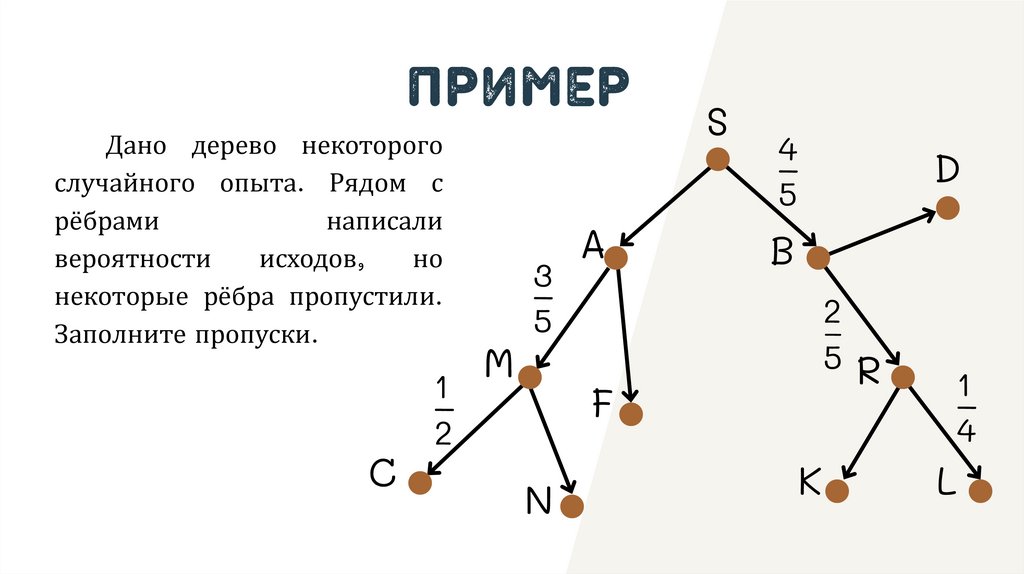
Пример
Дано дерево некоторого
случайного опыта. Рядом с
рёбрами
написали
вероятности
исходов,
но
некоторые рёбра пропустили.
Заполните пропуски.
C
1_
2
M
3
_
5
A
S
4
_
5
D
B
2_
5 R
F
N
K
1_
4
L

17.

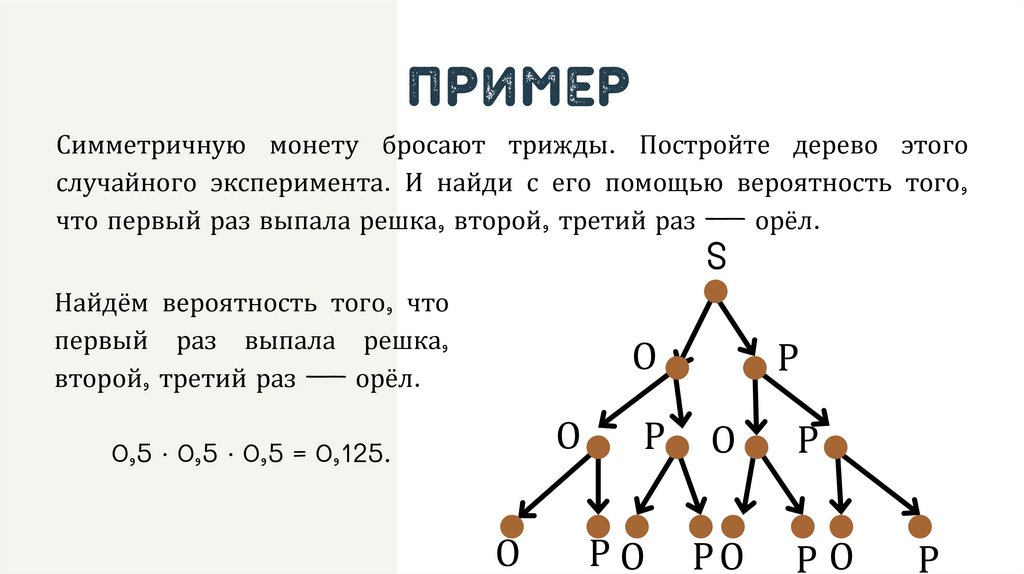
пример
Симметричную монету бросают трижды. Постройте дерево этого
случайного эксперимента. И найди с его помощью вероятность того,
что первый раз выпала решка, второй, третий раз — орёл.
S
Найдём вероятность того, что
первый раз выпала решка,
второй, третий раз — орёл.
О
О
0,5 ⋅ 0,5 ⋅ 0,5 = 0,125.
О
Р
Р
О
Р
РО
РО
РО
Р

18.

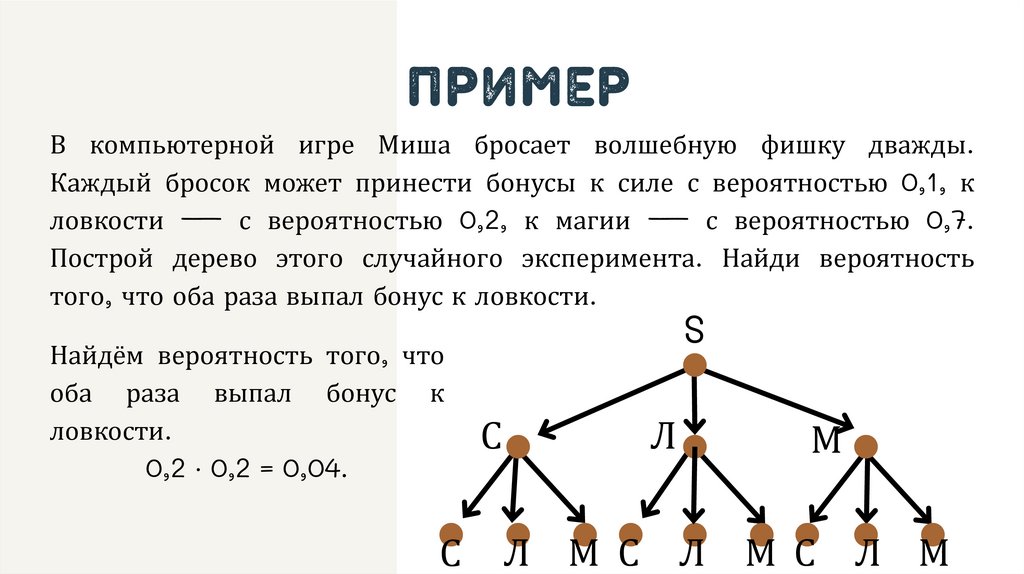
пример
В компьютерной игре Миша бросает волшебную фишку дважды.
Каждый бросок может принести бонусы к силе с вероятностью 0,1, к
ловкости — с вероятностью 0,2, к магии — с вероятностью 0,7.
Построй дерево этого случайного эксперимента. Найди вероятность
того, что оба раза выпал бонус к ловкости.
Найдём вероятность того, что
оба раза выпал бонус к
ловкости.
0,2 ⋅ 0,2 = 0,04.
С
S
С
Л
М
Л М С Л М С Л М

19.

§ 56, стр 42
№ 111, 113
домашнее
задание