Спин и четность ядер. Лекция 4

1.

2.

11. Полный момент количества движения (спин) ядра.
12. Принцип тождественности частиц. Квантовая
статистика.
13. Пространственная четность. Четность ядер.
14. Изотопический спин. Спектры ядер.
01.05.2024
2

3.

11. Полный момент количества движения ядра.
Вращательное движение частицы характеризуется моментом количества
движения (МКД), который в квантовой механике квантуется. При этом, согласно
правилам квантовой механики, одновременно можно определить модуль
вектора, и его проекцию на выбранное направление.
Для орбитального МКД имеем:
1 ,
z
max
,
где =0,1,2… – орбитальное квантовое число.
Остальные возможные проекции на тоже направление можно получить из
вычитая , т.е. величина проекции МКД может принимать всего 2 1
целочисленных значений. Только при 1 величина проекции практически
совпадает со значением МКД, а свойства микрочастицы со свойствами
классической частицы.
01.05.2024
3

4.

Многие частицы обладают собственным МКД, который имеет квантовую
природу и не связан с перемещением частицы как целого:
s s s 1 ,
s
z
max
s ,
где s – квантовое число спин (от англ. spin – вращаться, вертеться), может
равняться как целому, так и полуцелому числу s=0,1/2,1,3/2,2,.... Что же касается
электрона, протона и нейтрона, то у них максимальное значение проекции спина
равно 1/2.
01.05.2024
4

5.

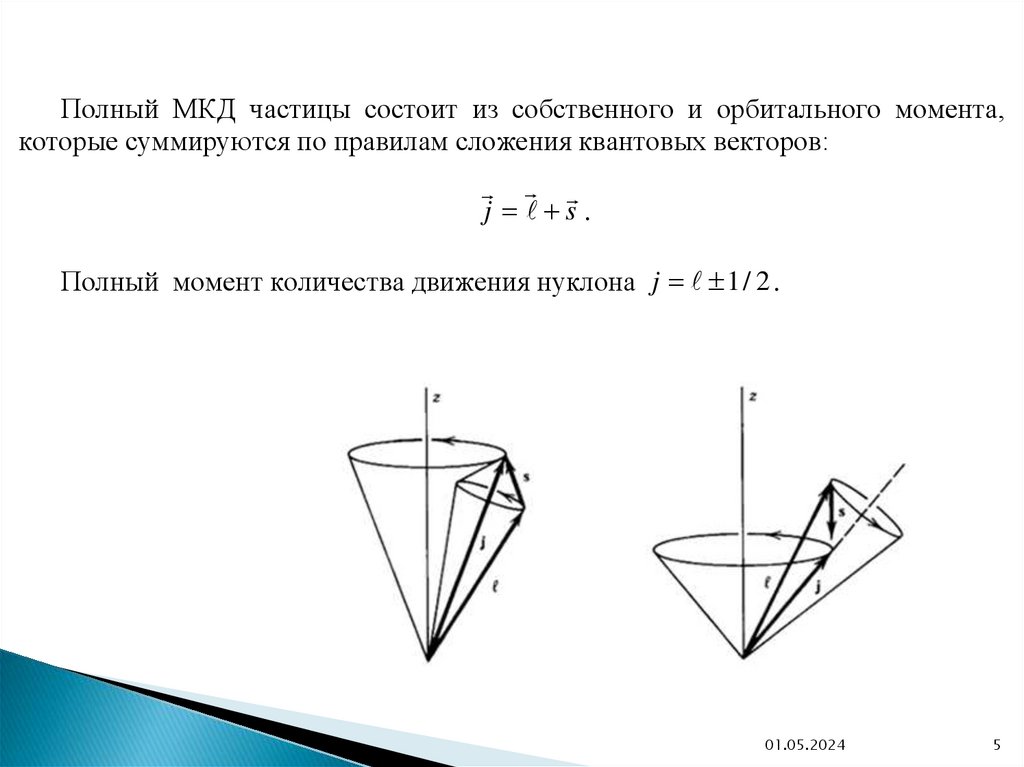
Полный МКД частицы состоит из собственного и орбитального момента,
которые суммируются по правилам сложения квантовых векторов:
j s .
Полный момент количества движения нуклона j 1 / 2 .
01.05.2024
5

6.

Полный МКД ядра состоит из МКД входящих в него протонов и нейтронов.
Последние в свою очередь обладают спиновым и орбитальным МКД,
обусловленным движением относительно общего центра инерции ядра. Атомное
ядро в каждом состоянии характеризуется полным моментом количества
движения J, который в системе покоя ядра называется спином ядра, поскольку,
как и для отдельного нуклона это внутренний момент движения системы-ядра,
рассматриваемого в целом как одна частица. Его можно получить двумя
способами, все зависит от того как взаимодействуют нуклоны:
A
A
1. (jj)-связь J ядра i s i j i .
i 1
i 1
A A
2. ( s )-связь J ядра L S , где L li , S si .
i 1
i 1
Тогда J J ( J 1) , J z mJ , mJ может принимать 2 J 1 значений от J до
-J, J L S , L S 1,..., L S .
Если ядро находится в состоянии с определенным значением спина и его
проекции, то оно описывается волновой функцией J ,m , которая является
2
собственной функцией операторов J z и J :
2
2
J J ,m J ( J 1) J ,m , J z J ,m mJ J ,m .
J
J
J
J
J
01.05.2024
6

7.

Для спинов атомных ядер экспериментально установлены следующие
закономерности:
если A – чётное, то J = n (n = 0, 1, 2, 3,...), т.е. спин ядра имеет
целочисленное значение;
если A – нечётное, то J = n + 1/2, т.е. спин ядра имеет полуцелое значение;
чётно-чётные ядра в основном состоянии имеют значение спина J = 0, что
указывает на взаимную компенсацию моментов нуклонов в основном
состоянии ядра – особое свойство межнуклонного взаимодействия;
cпины всех известных стабильных ядер не превышают 9 2 , т. е. очень
малы по сравнению с суммой абсолютных величин спинов и орбитальных
моментов всех входящих в ядро частиц. Этот факт свидетельствует о том,
что большинство нуклонов прочно связаны в замкнутых оболочках,
имеющих нулевой суммарный момент, и не участвует в создании спина
ядра.
Если частица обладает векторными или тензорными характеристиками
любой природы, то они должны
выражаться через вектор спина: A аJ , где a –
константа, характеризующая A .
01.05.2024
7

8.

12. Принцип тождественности частиц. Квантовая статистика.
В квантовой механике при рассмотрении систем частиц важную роль играет
принцип тождественности: если две частицы одного сорта, имеющие абсолютно
одинаковые (тождественные) свойства, поменять местами, то их невозможно
экспериментально различить.
Пусть r1 , J 1 , r2 , J 2 1,2 – волновая функция системы двух
тождественных частиц. Введем оператор перестановки P 12 и подействуем им
дважды на волновую функцию (1,2) .
Тогда P12 P12 (1,2) P12 (2,1) P12 (1,2) , отсюда собственное значение
оператора P12 1, т.е. возможны два случая:
P 12 (1,2) (2,1) – функция симметричная по частицам;
P 12 (1,2) (2,1) – функция антисимметричная по частицам.
01.05.2024
8

9.

Частицам одного сорта свойственен лишь один из этих типов симметрии. Это
называется квантовой статистикой. Она определяет коллективное поведение
системы тождественных частиц.
Частицы подчиняются статистике Бозе-Эйнштейна и называются бозонами,
если b (1,2,3,..., n) b (2,1,3,..., n) симметричная по частицам.
Частицы подчиняются статистике Ферми-Дирака и называются фермионами,
если f (1,2,3,..., n) f (2,1,3,..., n) антисимметричная.
Статистика тесным образом связана со спином частицы. Эта связь
доказывается в квантовой теории поля и носит название теоремы ПаулиЛюдерса. Одна из её формулировок гласит следующие: частицы с целым спином
подчиняются статистике Бозе-Эйнштейна ( S 0,1,2,... ), частицы с полуцелым
спином – статистике Ферми-Дирака ( S 1 / 2,3 / 2,5 / 2,... ).
С симметрией волновых функций связан также принцип Паули: в одном и
том же квантовом состоянии не может находиться более одного фермиона.
01.05.2024
9

10.

Сатьендра Нат Бо́зе или
Шотендронат Бо́шу —
индийский физик, специалистя
в математической физике. Один
из создателей квантовой
статистики (статистика Бозе —
Эйнштейна), теории конденсата
Бозе — Эйнштейна. В его честь
назвали бозон.
Родился: 1 января 1894 г., Калькутта, Индия
Умер: 4 февраля 1974 г. (80 лет), Калькутта, Индия
01.05.2024
10

11.

Поль Адриен Морис
Дира́к — английский физик-
теоретик, один из создателей
квантовой механики. Лауреат
Нобелевской премии по физике
1933 года (совместно с
Эрвином Шрёдингером).
Родился: 8 августа 1902 г., Бристоль, Великобритания
Умер: 20 октября 1984 г. (82 года), Таллахасси, Флорида, США
01.05.2024
11

12.

Во́льфганг Эрнст
Па́ули —
австро-швейцарский
физик-теоретик,
работавший в области
физики элементарных
частиц и квантовой
механики.
Лауреат
Нобелевской
премии
по физике за 1945 год.
Родился: 25 апреля 1900, Вена, Австро-Венгрия
Умер:
15 декабря 1958 (58 лет),Цюрих, Швейцария
01.05.2024
12

13.

13. Пространственная четность. Четность ядер.
Пространственная чётность характеризует свойства симметрии физической
величины при зеркальном отражении (пространственной инверсии). Это
квантовая характеристика системы частиц.
Пусть (r )
– волновая функция частицы. Введем оператор
пространственной инверсии P и подействуем им дважды на волновую функцию
(r ) . Тогда P( P (r )) P ( r ) P (r ) , отсюда собственное значение
оператора P 1, т.е. возможны два случая:
P (r ) ( r ) (r ) – функция является четной;
P (r ) ( r ) (r ) – функция является нечетной.
Если волновая функция не меняет свой знак при инверсии всех координат, то
состояние системы, которую она описывает, называется четным и обозначается
P 1, а если меняет – нечетным ( P 1 ).
01.05.2024
13

14.

Юджин Ви́гнер или
Енё Пал Вигнер —
венгерско-американский
физиктеоретик,
внёсший
вклад
в
математическую физику. Он получил
американское гражданство в 1937
году и Нобелевскую премию по
физике в 1963 году «за вклад в
теорию
атомного
ядра
и
элементарных частиц, в частности, за
открытие
и
применение
фундаментальных
принципов
симметрии».
Родился: 17 ноября 1902 г., Будапешт, Королевство Венгрия, Австро-Венгрия
Умер:
1 января 1995 г. (92 года), Принстон, Нью-Джерси, США
01.05.2024
14

15.

Кроме четности волновой функции, легко обнаруживаемой по известной
зависимости r , частицы обладают так называемой внутренней четностью. Её
происхождение можно определить как результат того, что частица имеет
некоторую внутреннюю структуру, так Pp Pn Pe 1, т.е. четные частицы.
В квантовой механике для изолированной системы четность не меняется с
течением времени. Четность системы из двух не взаимодействующих частиц A и
B определяется как произведение их внутренних четностей и четностей
волновых функций, описывающих движение частиц относительно центра
инерции:
PA B PB PA ( 1) ( 1) ,
(4.1)
B
A
где A и B – орбитальные квантовые числа характеризующие движение частиц.
Если между частицами действуют электромагнитные и ядерные силы, то
четность системы сохраняется, т.е. если система вначале имела четность +1, то
после взаимодействия у этой или новой системы частиц четность останется той
же. Но в слабых взаимодействиях закон сохранения четности не работает.
01.05.2024
15

16.

Если атомное ядро представлять в виде совокупности независимо
движущихся нуклонов, то четность ядра будет равна произведению внутренних
A
четностей нуклонов на ( 1)
i
i 1
в соответствии с формулой (4.1), т.е.
A
Pяд ( 1)
i
i 1
,
где i – орбитальное квантовое число определяющие характер движения
данного нуклона.
Внутренняя четность нуклона +1, значит, его состояние будет четное или
нечетное, в зависимости от четности , и четность системы нуклонов (ядра)
будет определяться суммой всех . Т.к. четность замкнутой системы
сохраняется, то четность ядра может измениться в результате испускания или
захвата частиц, находящихся в нечетном состоянии.
01.05.2024
16

17.

14. Изотопический спин ядра. Спектры ядер.
Как основное, так и возбужденные состояния ядер помимо
рассмотренных ранее энергии, спина и четности характеризуются
квантовыми числами, которые называются изоспином I (либо T) и
проекцией изоспина Iz (либо Tz).
Введение этих квантовых чисел связано с тем фактом, что ядерные
силы инвариантны относительно замены протонов на нейтроны. Это
особенно ярко проявляется в спектрах т.н. ”зеркальных” ядер, т.е.
ядер-изобар, у которых число протонов одного равно числу
нейтронов другого (например, 13C и 13N). Для всех известных пар
таких ядер имеет место подобие спектров низших возбужденных
состояний: спины и четности низших состояний одинаковы, а энергии
возбуждения близки.
01.05.2024
17

18.

С точки зрения теории изоспина, нейтрон и протон являются одной и той
же частицей – нуклоном с изоспином I = 1/2 – в двух разных состояниях,
различающихся проекцией изоспина на выделенную ось (Iz = I3) в
пространстве изоспина. Таких проекций для I = 1/2 может быть только две:
Iz = +1/2 (протон) и Iz = –1/2 (нейтрон).
Квантовая теория изоспина построена по аналогии с теорией спина. Однако
пространство
изоспина
не
совпадает
с
обычным
координатным
пространством. Каждой частице соответствует некоторое направление, на нем
откладывается вектор длины I. На изотопическую ось проектируют вектор.
Число возможных проекций (2I+1) равно числу зарядовых состояний
частицы.
Система Z протонов и N нейтронов – ядро – имеет проекцию изоспина
Iz (A,Z) = Z(+1/2) + N(–1/2) = (Z – N)/2.
Изоспин системы
составляющих:
нуклонов
является
векторной
суммой
01.05.2024
изоспинов
18

19.

Ядерные (т.е. сильные) взаимодействия не зависят от проекции изоспина,
или, точнее, сильные взаимодействия инвариантны относительно вращений в
изоспиновом пространстве. Однако от величины изоспина ядерные силы
зависят!
Низшим по энергии состояниям системы нуклонов, т.е. основным
состоянием ядра, является состояние с низшим возможным значением
изоспина, которое равно
I0 = |Iz| = |Z–N|/2 = |2Z–A|/2.
Возбужденные состояния ядер могут иметь более высокие значения изоспина,
но с той же проекцией.
Частицы или системы частиц, имеющие одинаковый изоспин и разные
проекции изоспина, составляют изоспиновые мультиплеты (дублеты, триплеты,
и т.д.). Особенностью членов такого мультиплета является то, что они
одинаковым образом участвуют в сильном взаимодействии. Простейший
пример дублета – нейтрон и протон. Состояния зеркальных ядер 17O (8
протонов, 9 нейтронов) и 17F (9 протонов, 8 нейтронов) являются другим
примером. Электромагнитное взаимодействие протонов ядра разрушает
изоспиновую симметрию.
01.05.2024
19

20.

Квантовый характер атомных ядер проявляется в картинах их
спектров возбуждения. На схемах спектров ядер указывают энергии
уровней ядра в МэВ или кэВ, а также спин, четность и изоспин
состояний (поскольку на схемах спектров даны энергии возбуждения
уровней, энергия основного состояния принимается за начало отсчета).
Каждый уровень характеризуется не только энергией, но и
определенной шириной Г. Поскольку каждый из возбужденных уровней
спектра имеет конечное среднее время жизни τ, то ширина уровня Г
также конечна и связана со средним временем жизни соотношением,
являющимся следствием соотношения неопределенности для энергии и
времени Δt·ΔE ≥ ћ, т.е. τ·Г ≥ ћ.
Ширина уровня Г ~ 10-2 эВ.
01.05.2024
20

21.

В области энергий возбуждения E < Eотд , т.е.
при энергиях, меньших, чем энергия отделения
нуклона, спектры ядер – дискретные.
Дискретный характер спектра возбуждений не
означает, что ширины уровней в этом спектре
равны 0. Это означает, что ширины спектральных
уровней меньше расстояния между уровнями
Г < ΔE.
Спонтанные переходы ядер из более высоких
возбужденных состояний дискретного спектра
ядра в более низкие (в том числе в основное
состояние) реализуются, как правило, путем
излучения
γ-квантов,
т.е.
за
счет
электромагнитных взаимодействий.
01.05.2024
21

22.

В области больших энергий возбуждения,
когда E > Eотд, ширины уровней возбужденного
ядра резко возрастают. Дело в том, что в
отделении нуклона от ядра главную роль играют
ядерные силы, т.е. сильные взаимодействия.
Вероятность сильных взаимодействий на порядки
выше вероятности электромагнитных, поэтому
ширины распада по сильным взаимодействиям
велики и уровни ядерных спектров в области
E > Eотд перекрываются – спектр ядра становится
непрерывным (ширины спектральных уровней
больше расстояния между уровнями Г > ΔE).
Главным
механизмом
распада
высоковозбужденных состояний из этой области
энергий
является
испускание
нуклонов
и
кластеров (α-частиц и дейтронов). Излучение γквантов в этой области высоких энергий
возбуждения E > Eотд происходит с меньшей
вероятностью,
чем
испускание
нуклонов.
Возбужденное
ядро
имеет,
как
правило,
несколько путей, или каналов, распада.
01.05.2024
22

23.

Спектр состояний ядра 12С
Спектр выше 16 МэВ является непрерывным.
Ширина уровня Г ~ 10-2 эВ.
01.05.2024
23