Similar presentations:
Треугольник Паскаля. Опыты с большим числом равновозможных элементарных событий
1.
Треугольник Паскаля.Опыты с большим числом
равновозможных элементарных
событий.
Вычисление вероятностей в опытах
с применением комбинаторных
формул. Испытания Бернулли.
Успех и неудача. Вероятности
событий в серии испытаний
Бернулли
2.
Историческая справка• Первое упоминание треугольника
Паскаля встречается в комментарии индийского
математика X века Халаюдхи. Треугольник
исследуется также Омаром Хайямом около 1100
года, поэтому в Иране эту схему называют
треугольником Хайяма. В 1303 году была
выпущена книга «Яшмовое зеркало четырёх
элементов» китайского математика Чжу Шицзе, в
которой был изображен треугольник Паскаля на
одной из иллюстраций; считается, что изобрёл
его другой китайский математик, Ян
Хуэй (поэтому китайцы называют его
треугольником Яна Хуэя). На титульном листе
учебника арифметики, написанном в 1529
году Петром Апианом, астрономом из
Ингольтштадского университета, также
изображён треугольник Паскаля. А в 1653 году (в
других источниках в 1655 году) вышла книга
Блеза Паскаля «Трактат об арифметическом
3.
• Паскаль умер, когда емубыло 39 лет, но, несмотря
на столь короткую жизнь,
он вошел в историю как
выдающийся математик,
физик, философ и
писатель. Его именем
благодарными потомками
названы единица
давления (паскаль) и
получивший чрезвычайно
широкое распространение
язык программирования.
4.
Что такое треугольник Паскаля?• Треугольник Паскаля
это арифметический
треугольник.
5.
Принцип построения треугольникаПаскаля
• Каждое число равно сумме 2-х чисел, стоящих над ним.
6.
Свойство № 1Треугольник Паскаля бесконечен
7.
Свойство № 2Сумма чисел в строках треугольника
Паскаля - 2n, где n - номер строки
1=2°
1+1=2¹
1+2+1=4=2²
1+3+3+1=8=2³
1+4+6+4+1=16= 24
8.
Свойство № 3Треугольник Паскаля симметричен
относительно центрального столбца
9.
Свойство № 4Первая диагональ треугольника Паскаля - это
натуральные числа, идущие по порядку.
10.
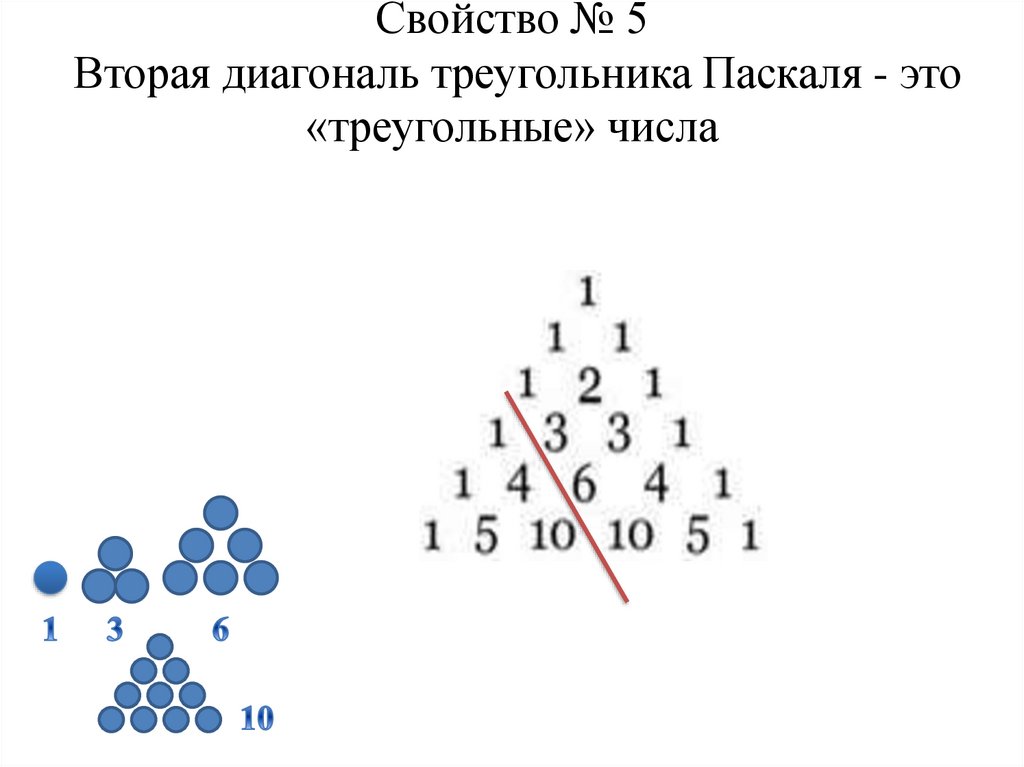
Свойство № 5Вторая диагональ треугольника Паскаля - это
«треугольные» числа
11.
Свойство № 6Третья диагональ треугольника Паскаля - это
«пирамидальные» числа
12.
Свойство № 7Каждое число треугольника Паскаля равно
сумме чисел предыдущей диагонали, стоящей
над этим числом.
1+2+3+4=10
13.
Свойство № 8В каждой строке треугольника Паскаля сумма чисел
на нечётных местах равна сумме чисел на чётных
местах.
1+6+1=4+4=8
14.
Свойство № 9Если номер строки треугольника Паскаля –
простое число, то все числа этой строки,
кроме 1, делятся на это число.
N=5
5,10,10,5- делятся на 5
15.
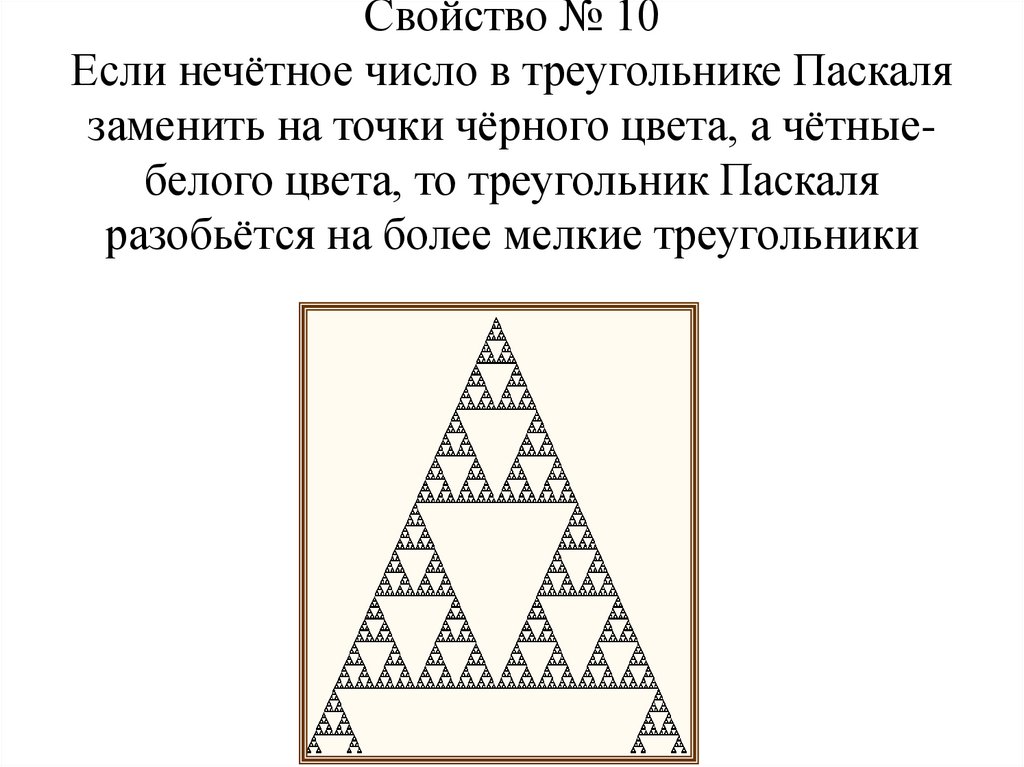
Свойство № 10Если нечётное число в треугольнике Паскаля
заменить на точки чёрного цвета, а чётныебелого цвета, то треугольник Паскаля
разобьётся на более мелкие треугольники
16.
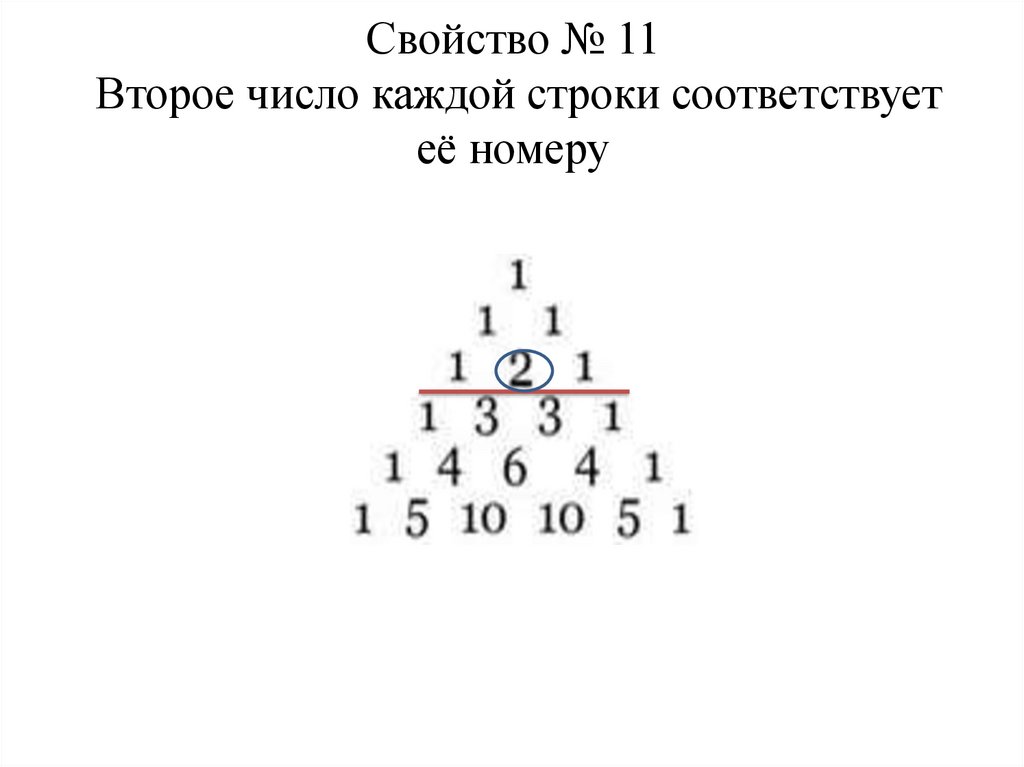
Свойство № 11Второе число каждой строки соответствует
её номеру
17.
Применение свойств треугольника Паскаля в решенииматематических задач
Свойства треугольника Паскаля, наверное, были
бы не столь значимы если бы на их основе
нельзя было решать математические задачи.
Рассмотрим задачи которые можно решат с
помощью треугольника Паскаля.
18.
Задача ( олимпиадная)В город А можно попасть по
единственному входу. На каждом
перекрестке дорога расходится на
две. В город вошли 210 человек.
На каждом перекрестке они
делятся пополам. Сколько
человек окажется на каждом
перекрестке, когда они уже не
смогут разделиться?
Ответ:1,10,45,120,
210,252,210,120,45,
10,1ч.
19.
Задача ( алгебраическая)Представить в виде многочлена
выражение (а+в)4
(а+в)0=1
(а+в)1=1а+1в
(а+в)2=1а2+2ав+1в2
……………………………….
(а+в)4=1а4+4а3в+6а2в2+4ав3+1в4

















 mathematics
mathematics