Similar presentations:
Теорема Пифагора
1.
Теорема Пифагора«Геометрия владеет двумя сокровищами:
одно из них – это теорема Пифагора…»
Иоганн Кеплер
c² = a² + b²
2.
«Теорема Пифагора»c² = a² + b²
с
b
а
3.
Исторический экскурсРассказ о Пифагоре(стр 115прочитайте)
Пифагор жил в
VI в. до н. э. в
Древней Греции
Основал
философскую
школу –
пифагорейский
союз.
4.
Пифагорейцы занималисьматематикой, философией,
естественными науками.
Ими были сделаны важные
открытия в арифметике и
геометрии. В школе
существовало правило, по
которому авторство всех
работ приписывалось
Пифагору. Так что
достоверно неизвестно,
какие открытия
принадлежат самому
ученому.
5.
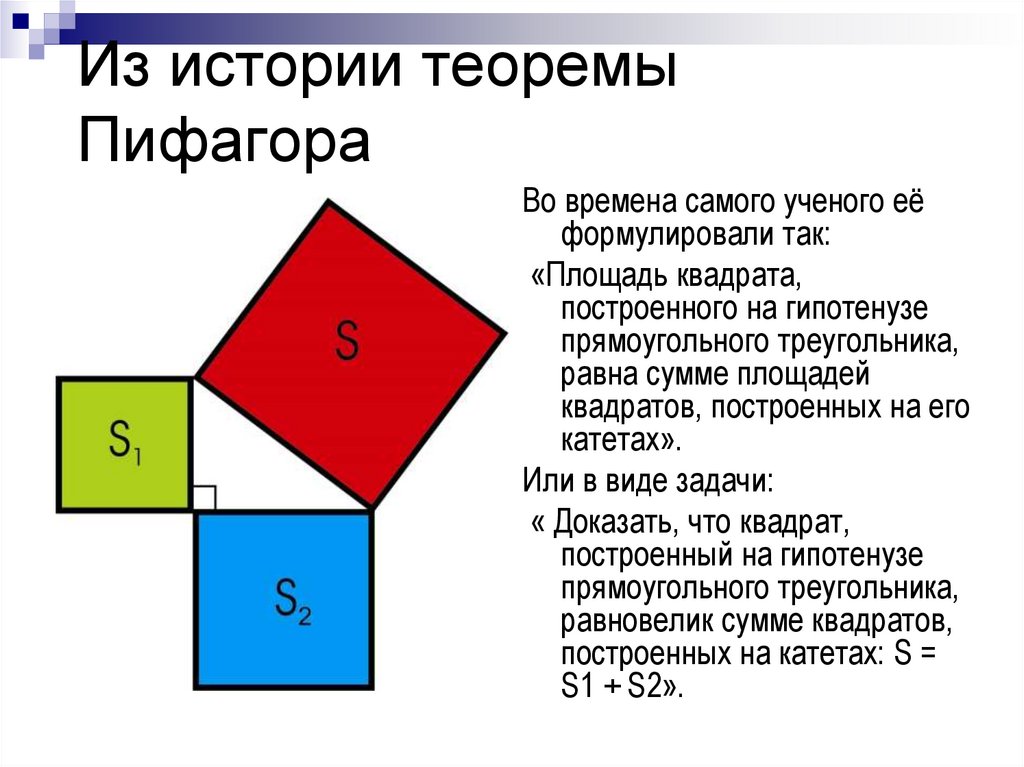
Из истории теоремыПифагора
Во времена самого ученого её
формулировали так:
«Площадь квадрата,
построенного на гипотенузе
прямоугольного треугольника,
равна сумме площадей
квадратов, построенных на его
катетах».
Или в виде задачи:
« Доказать, что квадрат,
построенный на гипотенузе
прямоугольного треугольника,
равновелик сумме квадратов,
построенных на катетах: S =
S1 + S2».
6.
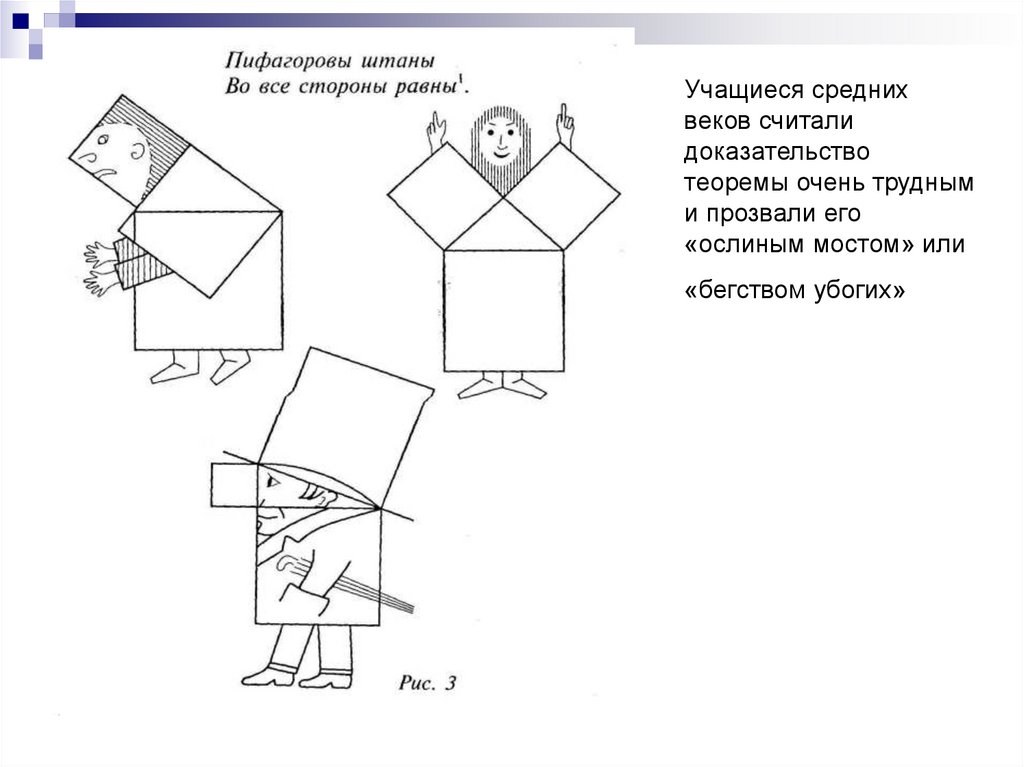
Учащиеся среднихвеков считали
доказательство
теоремы очень трудным
и прозвали его
«ослиным мостом» или
«бегством убогих»
7.
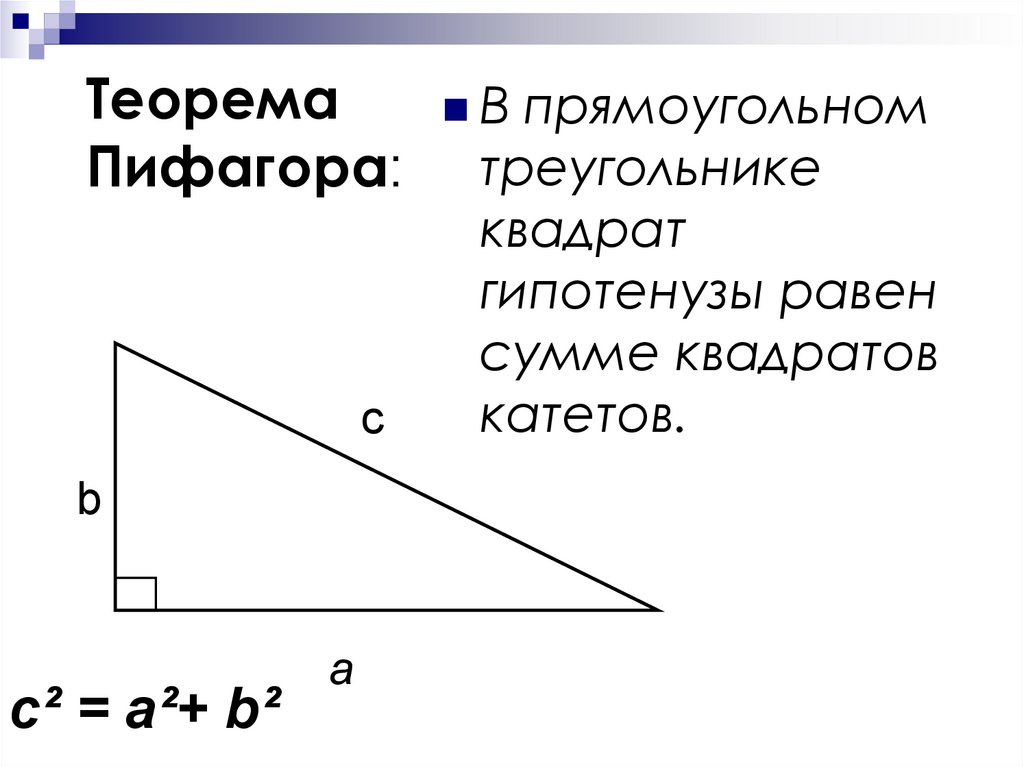
ТеоремаПифагора:
с
b
c² = a²+ b²
а
В
прямоугольном
треугольнике
квадрат
гипотенузы равен
сумме квадратов
катетов.
8.
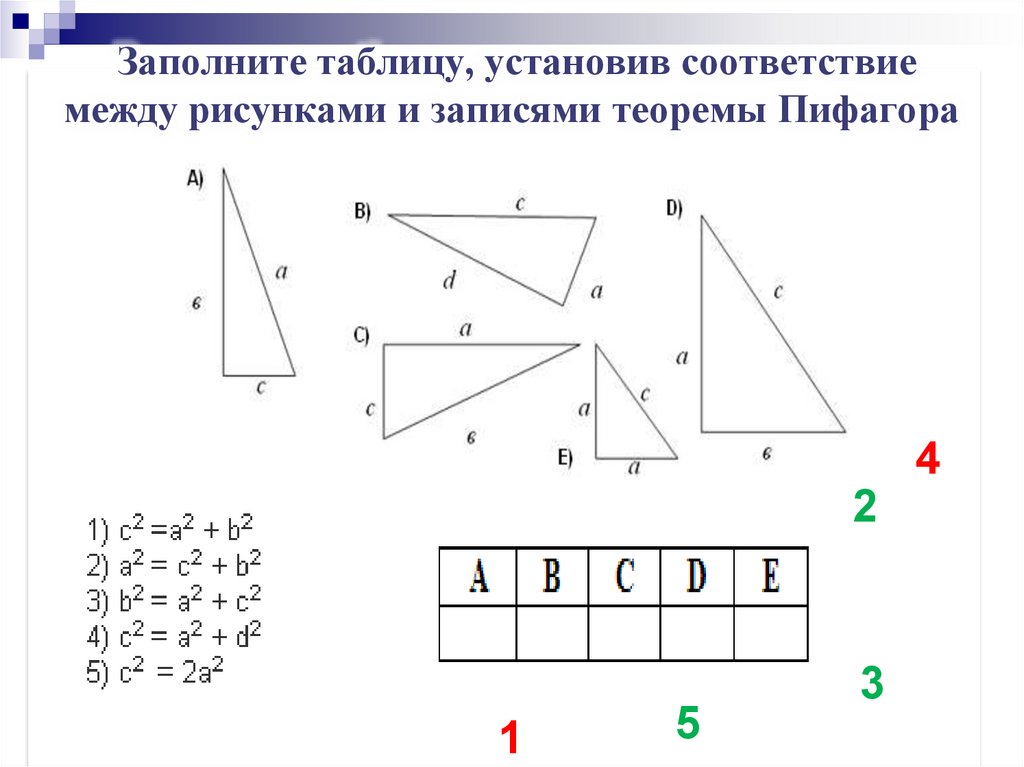
Заполните таблицу, установив соответствиемежду рисунками и записями теоремы Пифагора
4
2
1
5
3
9.
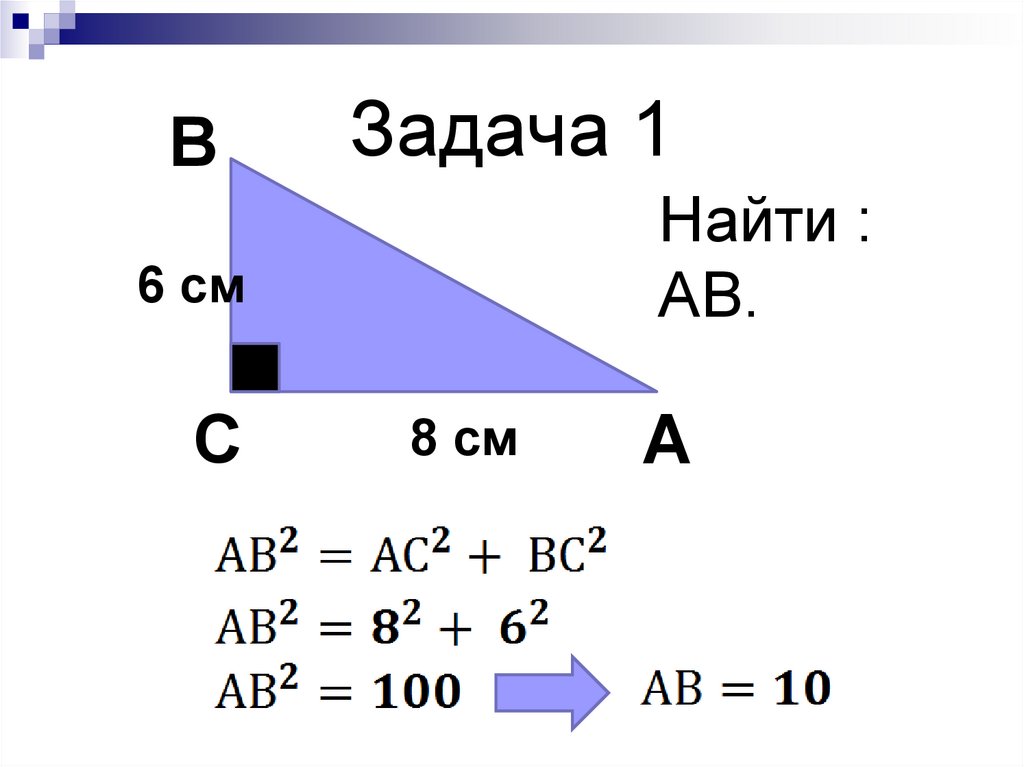
ВЗадача 1
Найти :
АВ.
6 см
С
8 см
А
10.
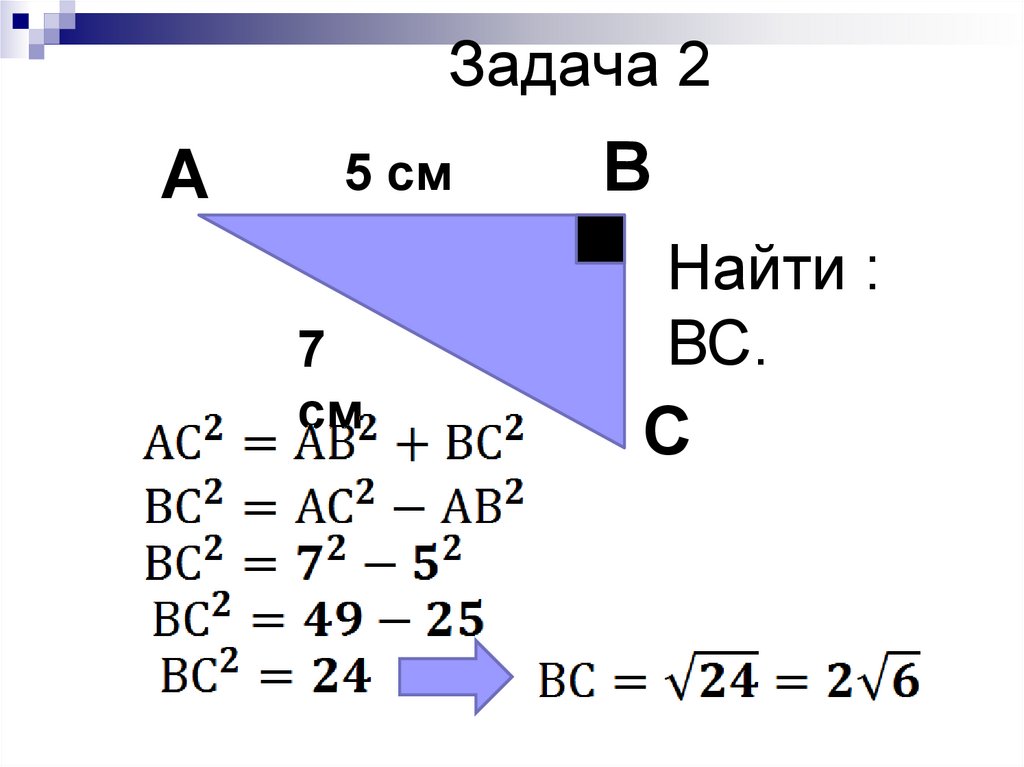
Задача 2А
5 см
7
см
В
Найти :
ВС.
С
11.
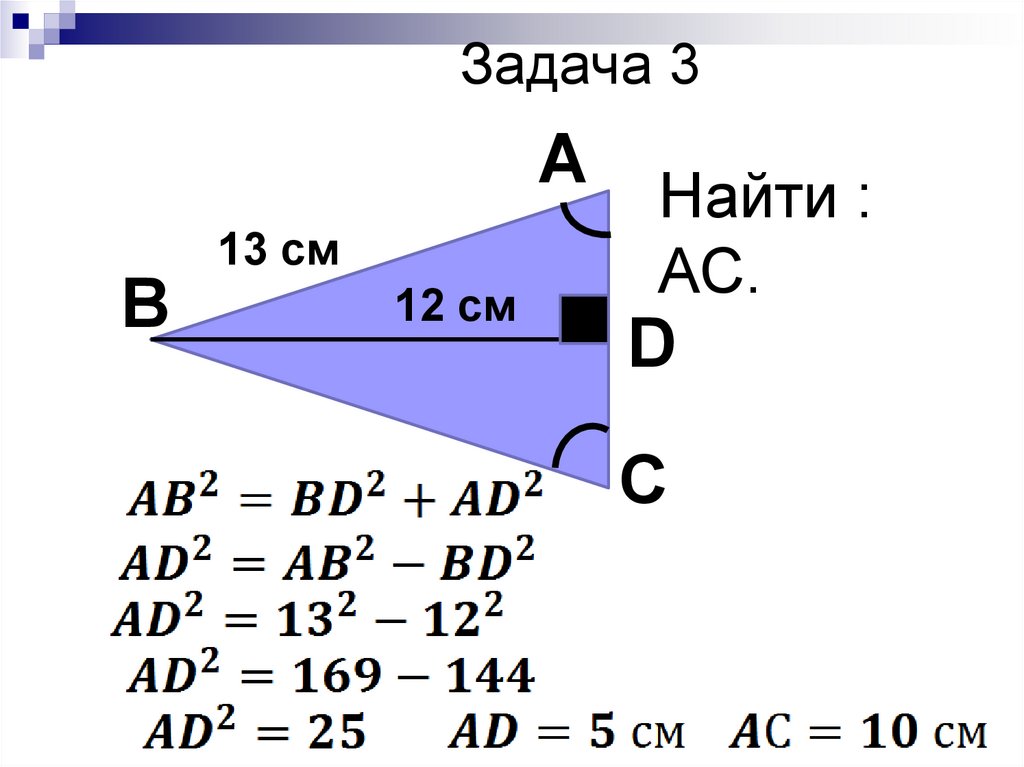
Задача 3А
В
13 см
12 см
Найти :
АС.
D
С
12.
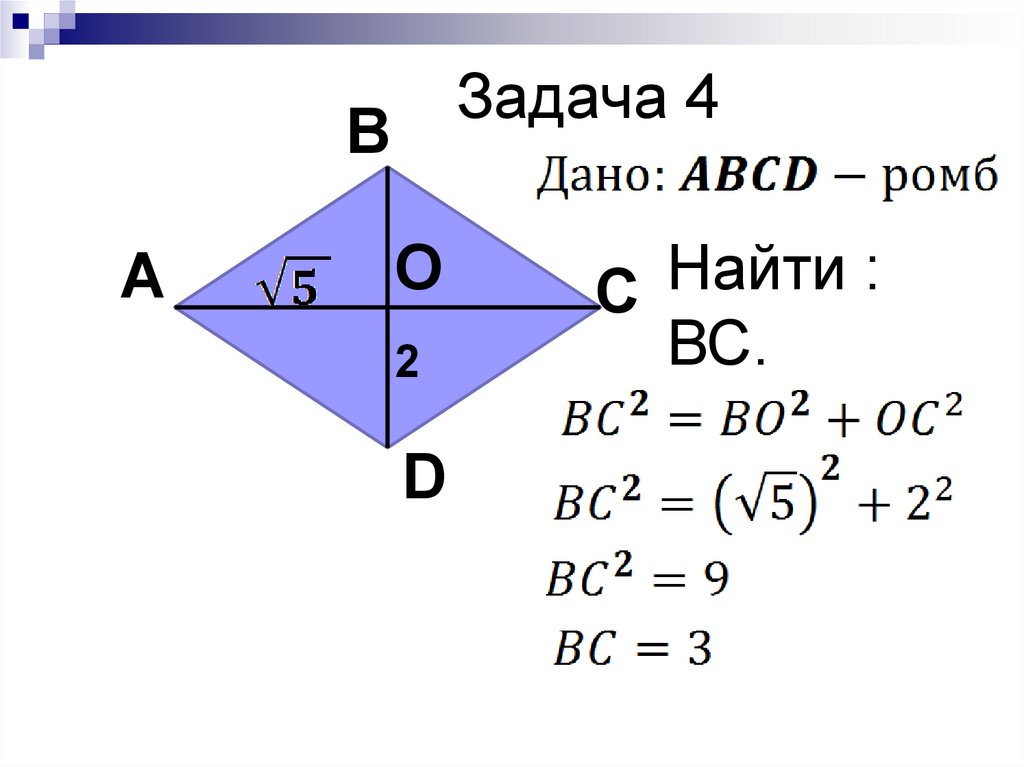
Задача 4В
А
О
2
D
Найти
:
С
ВС.
13.
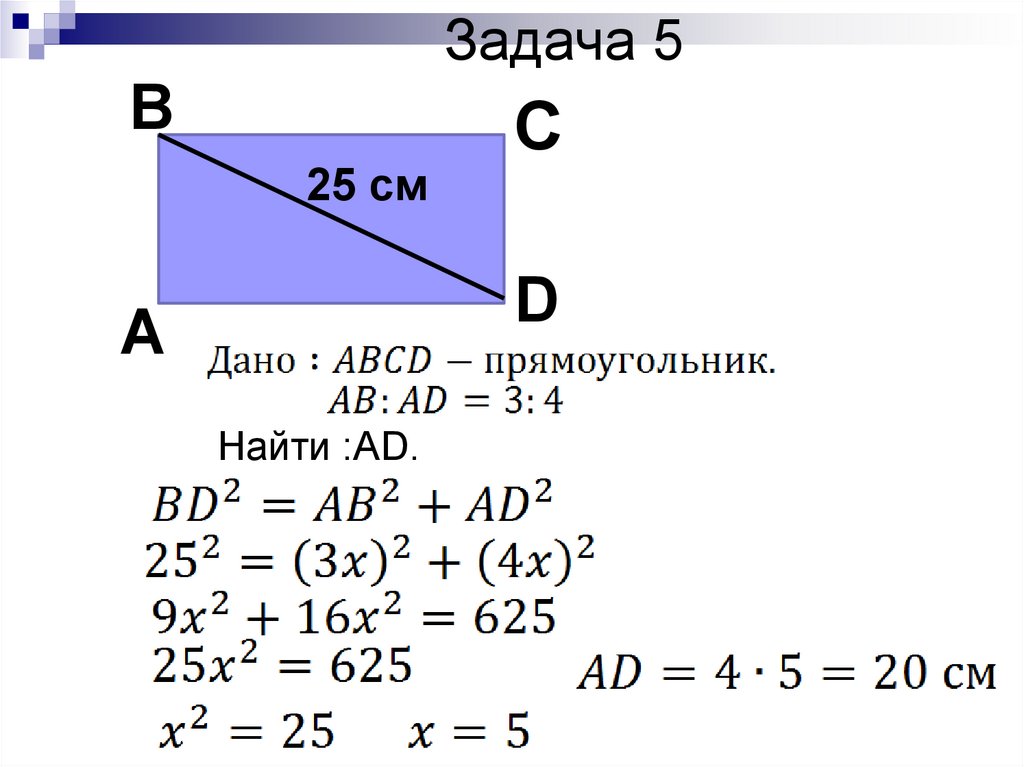
Задача 5В
25 см
С
D
А
Найти :AD.
14.
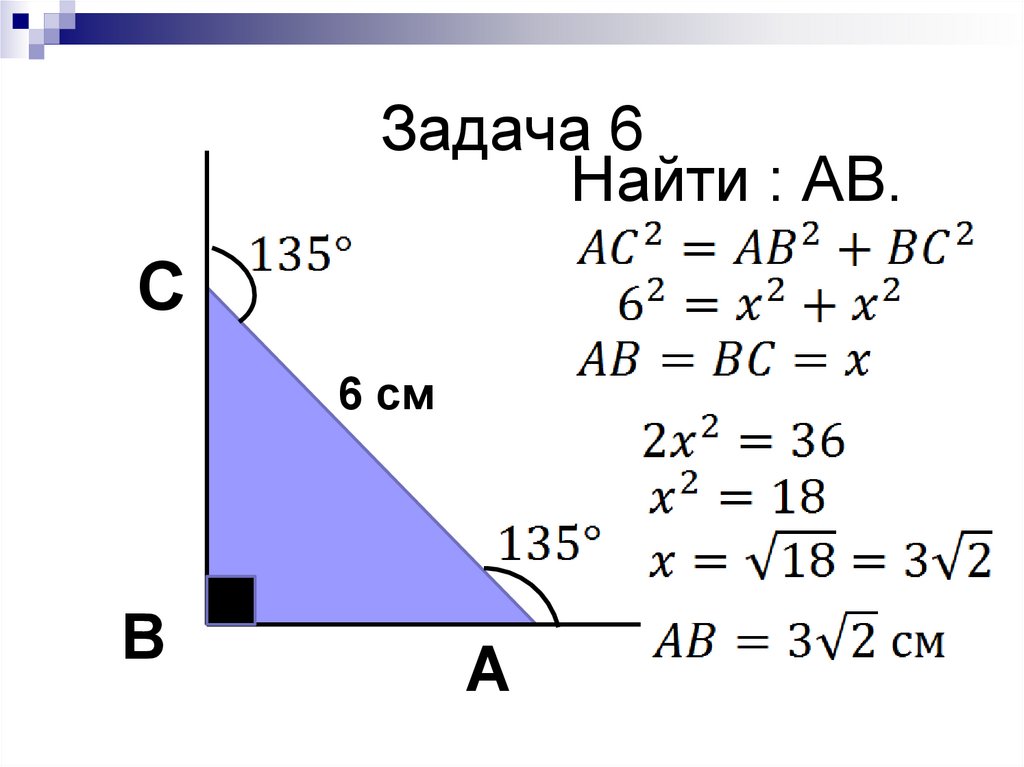
Задача 6Найти : АВ.
С
6 см
В
А
15.
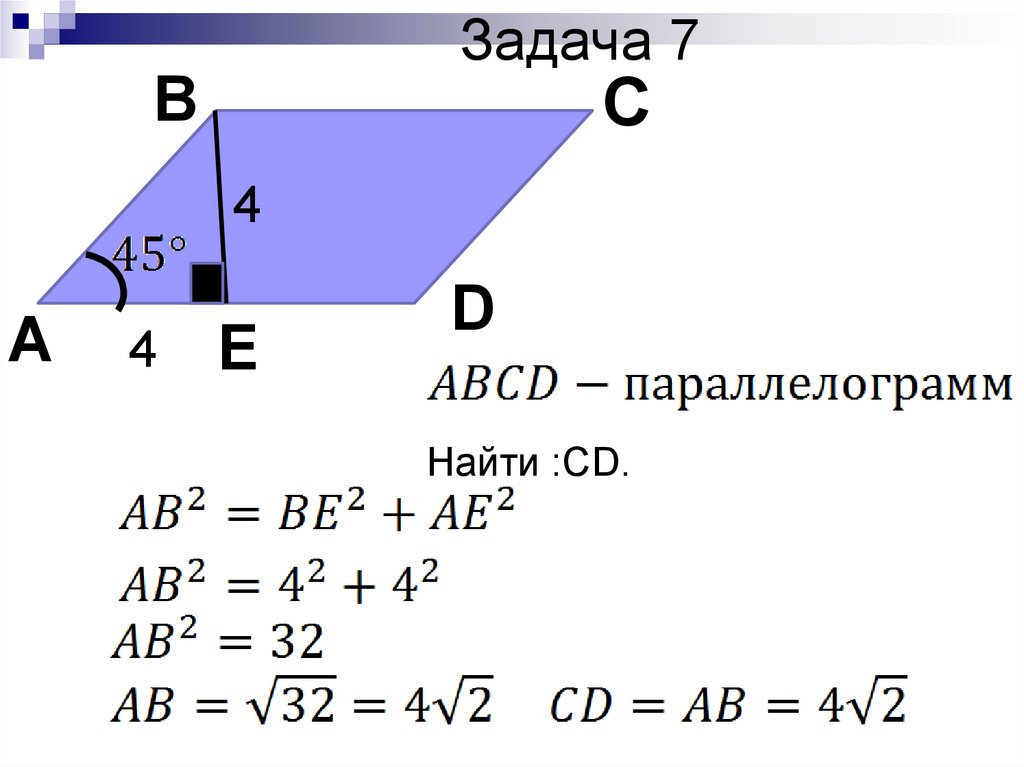
Задача 7В
С
4
А
4
Е
D
Найти :СD.





 mathematics
mathematics








