Similar presentations:
Основы квантовой оптики
1. Основы квантовой оптики
×ℏ2. Часть 1
3. Материалы
1. Клышко Д.Н. Физические основы квантовойэлектроники.
2. Клышко Д.Н. Фотоны и нелинейная оптика.
3. Глаубер Р. Оптическая когерентность и
статистика фотонов.
4. Глаубер Р. Сто лет квантам света // Успехи
физических наук. 2006. Vol. 176, № 12. P.
1342.
5. Мандель Л., Вольф Э. Оптическая
когерентность и квантовая оптика.
×ℏ
4. Аналитический сигнал
E r , t d E r , e i tE _ r , t
1
i t
E _ r ,
d
t
E_
r
,
t
e
2
E ( ) r , t d E r , e i t
E _ r , E _ r ,
0
E _( ) r , t d E _ r , e i t
0
E _ r , t E _ r , t
( )
( )
( )
E_ r , t E _ r , t E _ r , t 2 Re E _ r , t
( )
( )
5. Интенсивность и ее моменты
E( ) r , t E0 r , t e i t_E r , t E0 r , t e i t E0 r , t e i t 2 Re E0 r , t e i t
E( )
E( )
2
T
2
1 2
I r , t E r , t E0 r , t E ( ) r , t E ( ) r , t
2
E r ,t e
2
0
2i t
2
0
E
r ,t e
2 i t
2E0 r ,t e
i t
E r , t e
0
i t
T
2
6. Интенсивность и ее моменты
E( ) r , t E0 r , t e i t_E r , t E0 r , t e i t E0 r , t e i t 2 Re E0 r , t e i t
E( )
E( )
T
2
1 2
I r , t E r , t E0 r , t E ( ) r , t E ( ) r , t
2
I r ,t E _ r ,t E _ r ,t G
( )
( )
(1)
r
I n r , t E _( )n r , t E _( )n r , t G(n) r
2
T
2
7. Стабилизированный лазер
w I I I 0I
n
G I I I 0 d I I I
(n )
n
n
0
n
0
I
2
I I
I
2
2
2I I
I
2
I
2
I
2
0
8. Часть 2
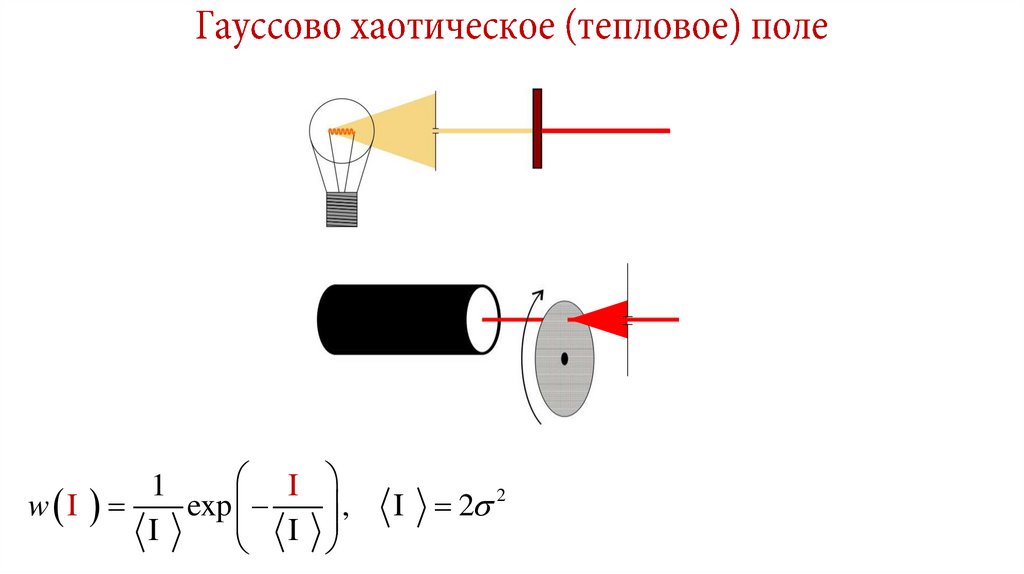
9. Гауссово хаотическое (тепловое) поле
E0 E0 i E02
E
0
w E0
exp 2 ,
2
2
2
E
0
w E0
exp 2
2
2
2
2
E0 E0
1
w E0 , E0 w E0 w E0
exp
2
2
2
2
1
1
I E0 r , t E0 2 E0 2
2
w I d E d E w E ,E E E I
0
0
0
0
2
0
2
0
I
1
I
2 exp 2
exp
I
2
2 I
1
,
I 2 2
10. Гауссово хаотическое (тепловое) поле
I1
w I
exp
I
I
,
I 2 2
11. Гауссово хаотическое (тепловое) поле
In
G n! I
(n )
b
n
b
u d v uv v d u
b
a
a
I
n 1
I
exp
I
I
0
I
n
d I I exp
I
I
d exp
I
I
1
w I
exp
I
I
0
,
I 2 2
a
I
n 1
nI exp
0 0
I
d I
n I G( n 1)
G 1
(0)
12. Гауссово хаотическое (тепловое) поле
In
G n! I
(n )
n
I
I
1
w I
exp
I
I
,
2
I
2
I 2 2
I
2
I
2
I
2
I
2
13. Часть 3
14. Корреляционные функции Глаубера
r1 ,t1 , 1(n )
( )
G1,2,...,
E
2n
1
En( ) En( 1)
E2( n )
G(n) t1 ,..., t2n G(n) t1 ,..., t2n
n
(1)
r1 , r2 ,t1 ,t2 t1 G r1 , r2 ,
(1)
r1 r2 r ,
G
G
(1)
15. Корреляционные функции Гауссового поля
(n )1,...,n,1 ,...,n
G
(2)
1,2 ,3, 4
G
( )
1
( )
3
E E
( )
2
E E
( )
4
(1)
G
(1)
1,1
G
( )
1
E E
(1)
n ,n
G
( )
4
( )
2
( )
3
E E
r1 , r2 , G r1 r2 ,
(1)
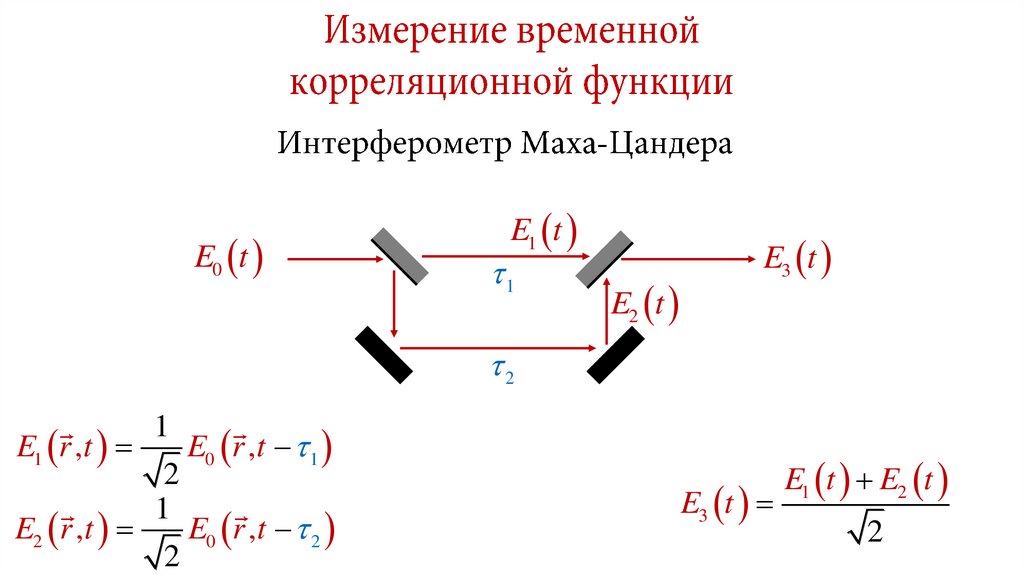
16. Измерение временной корреляционной функции
E0 tE1 t
1
E2 t
E3 t
2
E1 r , t
E2 r , t
1
2
1
2
E0 r , t 1
E0 r , t 2
E3 t
E1 t E2 t
2
17. Измерение временной корреляционной функции
1I 3 t E1 t E2 t E1 t E2 t
2
G12(1) 0
2
2
1
E1 t E2 t 2Re E1 t E2 t
2
2
2
1
E0 t 1 E0 t 2 2Re E0 t 1 E0 t 2
4
1
E1 r , t
E0 r , t 1
2
E1 t E2 t
E3 t
1
E2 r , t
E0 r , t 2
2
2
18. Измерение временной корреляционной функции
1I 3 t E1 t E2 t E1 t E2 t
2
G12(1) 0
2
2
1
E1 t E2 t 2Re E1 t E2 t
2
2
2
1
E0 t 1 E0 t 2 2Re E0 t 1 E0 t 2
4
(1)
0
G
1 2
19. Часть 4
20. Распространение корреляций
r rR b
b
E0 _ r , z d d r E0 _ r , z 0 exp i kR
2
2
R2 d 2 r r d 2 r 2 r 2 2r r b2 2r r
b2
y
a
d
d 2 b2
y
x
r
r 2 ~ a2
x
R
r
b
d
d
a2
z
A A 1 2 A 1 2 A
A
2A
2A
2
21. Распространение корреляций
r rR b
b
E0 _ r , z d d r E0 _ r , z 0 exp i kR
2
E0 _ r , z d e
(1)
G
i kb
k
d r E0 _ r , z 0 exp i b r r
2
r 1 , r 2 E _ r 1 E0 _ r 2
0
r2 r2 r1 r1
d r1 d r2 E _ r1 E0 _ r2 exp i k
b1
b2
2
2
0
I 0 r1 2 r1 r2
b1 b2 d
r2 r1 r1 / d
22. Распространение корреляций
kG d r I 0 r exp i r
d
(1)
(1)
G
2
r 1 , r 2 E _ r 1 E0 _ r 2
0
r2 r2 r1 r1
d r1 d r2 E _ r1 E0 _ r2 exp i k
b1
b2
2
2
0
I 0 r1 2 r1 r2
b1 b2 d
r2 r1 r1 / d
23. Теорема ван Циттерта-Цернике
kG d r I 0 r exp i r
d
(1)
(1889-1959)
2
(1888-1966)
24. Теорема ван Циттерта-Цернике
kG d r I 0 r exp i r
d
(1)
2
y
2 d d
coh ~
k r
a
y
x
a
x
r
d
z
a
25. Часть 5
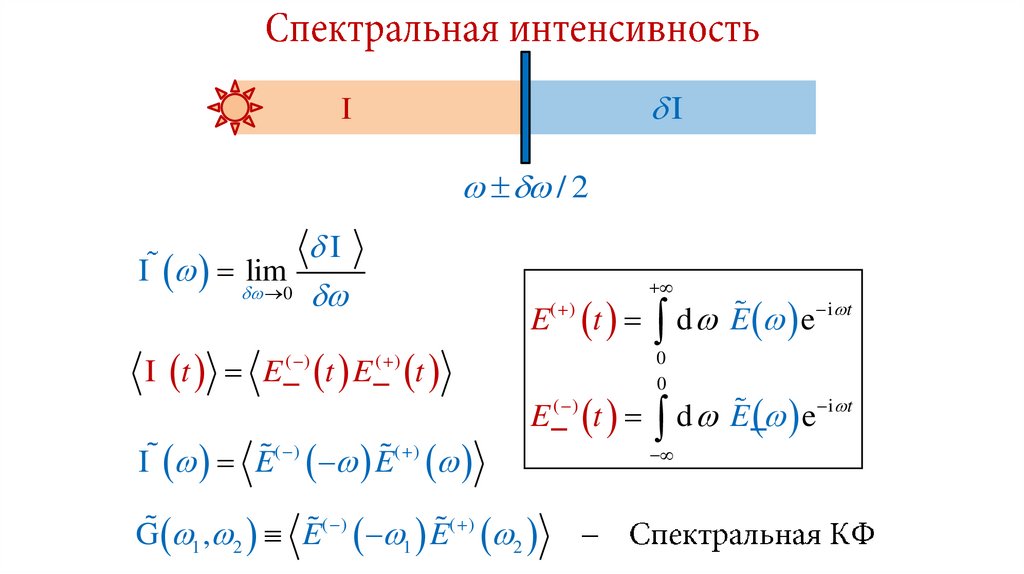
26. Спектральная интенсивность
II
/ 2
I
I lim
0
I t E _ t E _ t
( )
( )
I E ( ) E ( )
E ( ) t d E e i t
0
0
E _( ) t d E _ e i t
G 1 , 2 E ( ) 1 E ( ) 2
27. Связь между спектральной и временной КФ
G 1 , 2 E ( ) 1 E ( ) 21
d t d t E t e
4
( )
2
1
2
i 1t1
E
1
( )
t2 e
i 2t 2
E ( ) t E ( ) t G
1
d t1 d G e
2
i 2 1 t1
e
i 2
4
1
i 2
d
G
e
2 1
2
I 2 2 1
dt e
i 2 1 t1
1
2
2 1
1
i
I
d G e
2
28. Теорема Винера-Хинчина
1i
I
d G e
2
(1894-1964)
(1894-1959)
29. Теорема Винера-Хинчина
1i
I
d G e
2
G 2 d I e i
0
2
coh ~
30. Часть 6
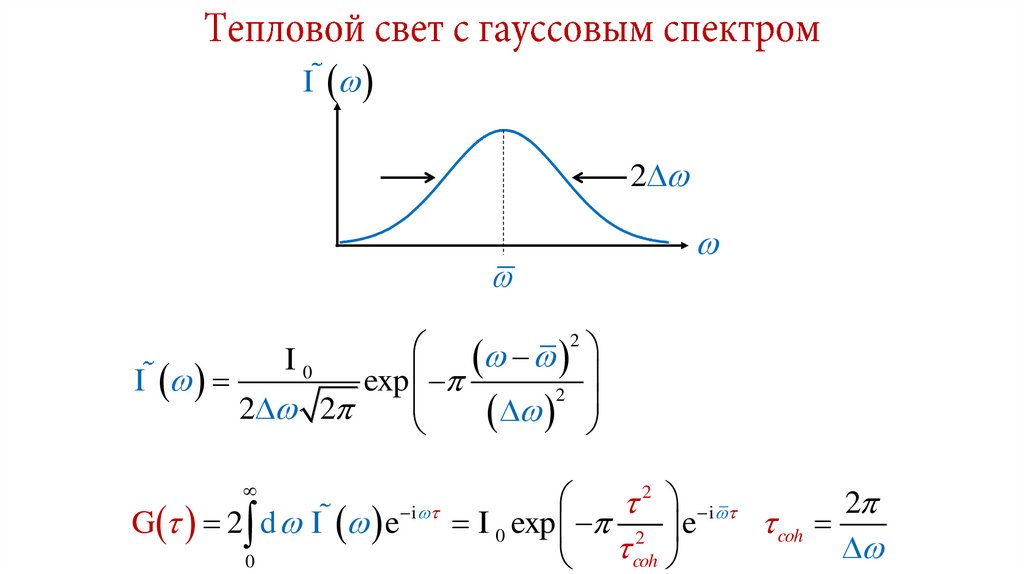
31. Тепловой свет с гауссовым спектром
I2
2
I0
I
exp
2
2 2
2
i
2
i
coh
G 2 d I e
I 0 exp 2 e
coh
0
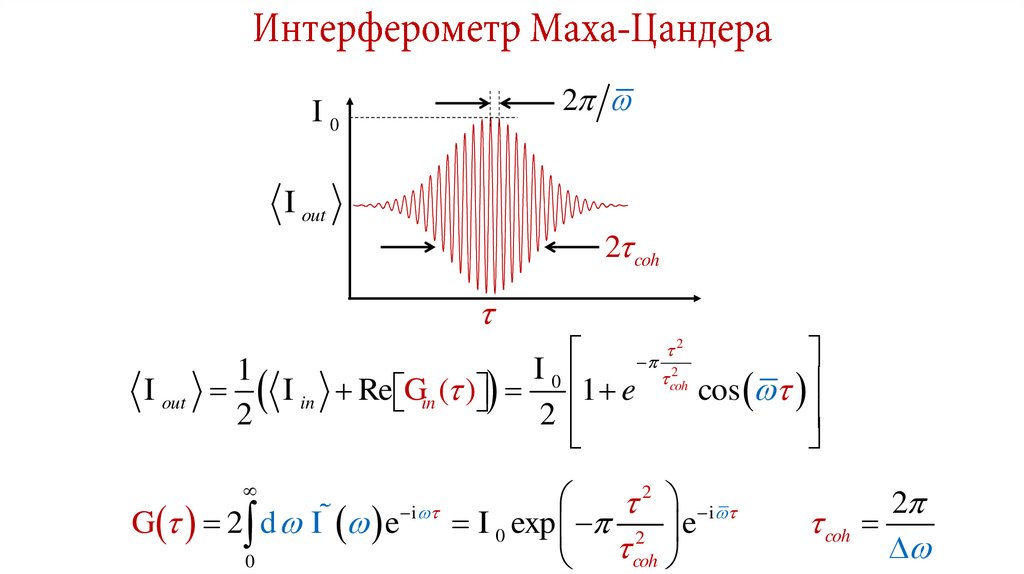
32. Интерферометр Маха-Цандера
Ein tEout t
I out
I
1
I in Re Gin ( ) 0 1 e
2
2
2
2
coh
cos
2
i
2
i
coh
G 2 d I e
I 0 exp 2 e
coh
0
33. Интерферометр Маха-Цандера
2I0
I out
2 coh
I out
I
1
I in Re Gin ( ) 0 1 e
2
2
2
2
coh
cos
2
i
i
G 2 d I e
I 0 exp 2 e
coh
0
2
coh
34. Интерферометр Юнга
E0 x E0 x1 ei kl1 E0 x2 ei kl2x1
x 2
l1
x
l2
l2 l1
x
L
L
i k l l
I x E0 x1 E0 x2 2Re E0 x1 E0 x2 e 2 1
2
2
(1)
k
I x I 1 I 2 2Re G ( ) exp i
x
L
35. Интерферометр Юнга
E0 x E0 x1 ei kl1 E0 x2 ei kl2x1
x 2
l1
l2
x
l2 l1
x
L
L
max min
V
G(1) ( )
max min
(1)
k
I x I 1 I 2 2Re G ( ) exp i
x
L
36. Интерферометр Юнга
kG d r I 0 r exp i r
d
(1)
x1
x 2
2
V
coh ~
max min
V
G(1) ( )
max min
(1)
k
I x I 1 I 2 2Re G ( ) exp i
x
L































 physics
physics







