Similar presentations:
Teoria câmpului electromagnetic
1.
TEORIA CÂMPULUIELECTROMAGNETIC
Prof. univ. dr. ing. Viorel VARVARA
Capitolul 1
Câmpul electrostatic în vid
1
2.
Lipsa cunoaşterii creează superstiţiiVIDEO (44)
VIDEO (43)
2
3. 1.1. Generalităţi despre electricitate
Electricitatea şi magnetismul sunt mereu prezente în jurul nostru.Avem ceasuri electrice, microfoane, calculatoare, televizoare,
radiouri.
Maşinile, avioanele, trenurile funcţionează datorită electricităţii.
3
4. 1.1. Generalităţi despre electricitate
Lumina este un fenomen electromagnetic. Undele radio, la fel.Culorile din curcubeul de pe cerul albastru apar datorită
electricităţii.
4
5. 1.1. Generalităţi despre electricitate
Animalele, pentru a se deplasa, au nevoie de electricitate deoarececontracţia muşchilor are nevoie de un curent electric.
Sistemul nervos este condus de electricitate.
Atomii, moleculele,
electricităţii.
Nu am putea vedea fără electricitate.
toate
reacţiile
chimice
există
datorită
5
6. 1.1. Generalităţi despre electricitate
Inima nu ar putea bate fără electricitate !6
7. 1.1. Generalităţi despre electricitate
Şi nu am putea gândi fără electricitate !7
8. 1.2. Nucleul atomului. Protonii, Neutronii
qe q p 1,6 10 19 C1.2. Nucleul atomului. Protonii,
Neutronii
Ce ştim despre ATOM ?
Ştim că are un NUCLEU (cu dimensiuni foarte mici în comparaţie cu atomul), în
jurul căruia gravitează ELECTRONII (într-un nor).
NUCLEUL este alcătuit din:
Protoni
au sarcină pozitivă
NUCLEU
q p 1,6 10 19 C
au masă
mp 1,7 10 27 kg
q =0
neutron n
mn = mp
qp = +1 ,6 10-19 C
-2 7
prot on
m p= +1 ,7 10 kg
-19
q = q p= -1,6 10 C
electro n e
-31
me= 9,1 10 kg
Neutroni
nu au sarcină
Forţe de atr acţie
electro static ă
qn 0
au masă
mn mp 1,7 10 27 kg
diametrul
nucleului
diametrul atomului
8
9. Continuare Nucleul atomului. Protonii, Neutronii
Nucleul atomului. Protonii,Neutronii
Continuare
ELECTRONII
au sarcină electrică negativă
qe q p 1,6 10 19 C
NUCLEU
q =0
neutron n
mn = mp
qp = +1 ,6 10-19 C
-2 7
prot on
m p= +1 ,7 10 kg
-19
q = q p= -1,6 10 C
electro n e
-31
me= 9,1 10 kg
au masă
me 9,1 10 31 kg
Forţe de atr acţie
electro static ă
diametrul
nucleului
diametrul atomului
m p 1836 me
Diametrul nucleului este 10-14 m .
Diametrul atomului este 10-10 m
Dacă am pune 7 miliarde de atomi în linie am obţine o lungime doar de 0,7m
.
9
10. 1.3. Sarcina electrică
Sarcina electrică nu poate fi creată din nimic.Dacă creezi o sarcină pozitivă undeva, obligatoriu, altundeva va apare o
sarcină negativă.
Pe ansamblu sarcina pozitivă cu cea negativă dau tot zero.
Prin urmare, noi nu creăm sarcina, ci o distribuim.
Punem undeva plus (+) şi altundeva apare minus (-).
Legea conservării sarcinii electrice:
Într-un sistem izolat sarcina este întotdeauna constantă.
10
11. Continuare Sarcina electrică
Observaţii :Unele materiale pot „ceda” uşor electroni şi altele materiale pot
„primi” electroni.
La unele materiale forţa cu care nucleul „ţine” e- în cadrul structurii
atomului este mică. Aceste materiale pot ceda uşor electroni (şi devin
încărcate pozitiv). De exemplu: palmele, părul uman, nailonul, hârtia,
sunt în topul materialelor care cedează uşor e- şi devin rapid încărcate
pozitiv (+)
Alte materiale pot capta uşor e- şi devin încărcate negativ (-).
11
12. 1.4. Generatorul Van de Graaff
Este cel mai simplu dispozitiv care poate crea sarcini electrice.9
8
2
2
3
3
4
4
5
5
10
6
7
6
7
8
9
10
12
13. Cum funcţionează generatorul Van de Graaff
Iniţial, cupola 1 este neutră (numărul de sarcinipozitive (+) este egal cu numărul de sarcini
negative (-)).
Tamburul inferior 6 este pus în mişcare de un
motor.
Prin frecare apar sarcini negative (-) pe partea
dreaptă a curelei 5. Aceste sarcini sunt preluate
de peria inferioară 7 şi depozitaţi pe cilindrul
metalic 10.
Pentru că pe cureaua 5 au apărut sarcini
negative (-) , obligatoriu, conform legii
conservării energiei, trebuie să apară şi sarcini
pozitive (+) pe cureaua 4.
10
13
14. Continuare Cum funcţionează generatorul Van de Graaff
Când sarcinile pozitive (+) ajung pe tamburul 3,sarcinile negative (-) de pe cupola 1 sunt atrase
şi vin prin peria 2 să neutralizeze sarcinile
pozitive (+) de pe tamburul 3. Astfel, pe cupola 1
există un surplus de sarcini pozitive (+), deci
cupola 1 este încărcată pozitiv.
Tija sferică 8 fiind legată de cilindrul 10 se
încarcă negativ.
10
Încărcarea cupolei 1 continuă atâta timp cât motorul roteşte tamburul 6.
Totuşi există o limită până la care se pot acumula sarcini pe cupola 1. Atâta
timp cât distanţa dintre cupola 1 şi tija sferică 8 este suficient de mare,
cupola 1 este un generator de sarcini pozitive.
Dacă dorim descărcarea de sarcini a cupolei 1 se apropie tija sferică 8.
Pentru că între acestea există o diferenţă de potenţial, la o distanţă suficient
de mică se va produce o scânteie. Din acest moment cupola 1 este
descărcată.
14
15.
Generatorul Van de GraaffVIDEO (49)
15
16.
Poate cineva atinge un obiect aflat la o tensiune de 200.000 V.experiment cu Generatorul Van de Graaff
VIDEO (65)
65. Shoud a person touch 200.000 V. An experiment with a Van de Graaff generator
http://www.youtube.com/watch?v=ubZuSZYVBng
16
17.
“Nu tensiunea te omoară, ci intensitatea”VIDEO (64)
64. It’s not de voltage that kills you it’s the Amps.
http://www.youtube.com/watch?v=8xONZcBJh5A
17
18. 1.5. Cum apar sarcinile electrice?
Un corp poate fi încărcat cu sarcină electrică prin:FRECARE
INDUCŢIE
ATINGERE
18
19. 1.5.1. Încărcarea unui corp izolator cu sarcini electrice prin FRECARE
Corpurile conductoare nu pot acumula sarcini electrice prin frecare.Numai corpurile izolatoare pot acumula sarcini electrice prin frecare.
Dacă freci o bucată de cauciuc cu o blana de pisică sau iepure, cauciucul
se încarcă cu sarcină negativă (-).
Dar unde este sarcina pozitivă (+)
care obligatoriu apare ?
Aceasta este pe blană.
Dacă freci o bucată de sticlă cu o cârpă de bumbac, sticla se încarcă cu
sarcină pozitivă (+).
19
20. Exemple de situaţii în care poate apărea încărcarea prin frecare:
Dacă te deplasezi pe un covor electroizolant rămâi încărcat cu sarcinăcând ai ieşit de pe covor.
Dacă îţi piepteni părul uscat cu un pieptene de plastic, părul tău
rămâne încărcat cu sarcină.
Când mergi, prin frecare, apar sarcini electrice pe ciorapi. Acest lucru
face ca ciorapii să atragă rochia şi aceasta să se muleze pe trup.
Când cobori scara blocului şi freci mâna de balustrada de plastic, mâna
se încarcă cu sarcină (şi între ea şi metalul balustradei poate apare o
mică scânteie).
Când cobori din maşină eşti încărcat electrostatic.
Când despachetezi ceva ambalat în plastic, te încarci cu sarcină
electrică statică.
20
21. FRECAREA creează sarcini electrice.
VIDEO (1)21
22. 1.5.2. Încărcarea unui corp conductor cu sarcini electrice prin INDUCŢIE ELECTRICĂ
Dacă apropii un corp încărcat electric (corp C) de un corp conductorneîncărcat, acesta din urmă se încarcă local cu sarcină de semn contrar
(prin inducţiei electrică
Corpul ce se încarcă prin INDUCŢIE
Dacă a apărut o
sarcină ( ),
obligatoriu apare
şi o sarcină ( )
Astfel, pe ansamblu,
corpul rămâne neutru,
aşa cu era iniţial
Pentru că
sarcinile ( ) ale
corpului ( C )
atrag sarcinile ( ) ,
sarcina distribuită
local este ( )
Corp ( C ) încărcat
cu sarcină ( )
22
23. Sarcini electrice apărute prin INDUCŢIE
VIDEO (2)23
24. Continuare 1.5.2. Încărcarea unui corp conductor cu sarcini electrice prin INDUCŢIE ELECTRICĂ
Observaţii:F
sarcinile electrice de semne contrare
se atrag
F
Sarcinile de semne contrare se atrag
sarcinile electrice de acelaşi semn se
F
F
resping
Sarcinile de acelaşi semn se resping
Între două corpuri:
încărcate cu cantităţi diferite de sarcină de acelaşi semn
încărcate cu cantităţi diferite de sarcină de semne contrare
există o diferenţă de potenţial (o tensiune electrică)
24
25. Sarcinile electrice de semne contrare se atrag (Opposites attract)
VIDEO (47)25
26. Continuare 1.5.2. Încărcarea unui corp conductor cu sarcini electrice prin INDUCŢIE ELECTRICĂ
ExempleÎncarc un student cu sarcină electrică „lovindu-l” cu blana de pisică.
Preferabil ca el să fie îmbrăcat cu un produs de nylon şi nu ceva de
bumbac.
Studentul stă pe un covor izolant.
Profesorul stă tot pe un covor izolant şi prin inducţie se încarcă şi el cu
sarcină (dar de semn contrar)
Amândoi apucă capetele unui tub de neon.
Cei doi, având sarcini (+) şi respectiv (-), la capetele tubului este o
tensiune electrică care face ca tubul să se aprindă.
26
27. Tubul de neon se aprinde datorita TENSIUNII electrice ce apare între cele 2 corpuri.
VIDEO (3)27
28. Generatorul Van de Graaff.
Cel mai cunoscut dispozitiv prin care se produc sarcini electrice esteGeneratorul Van de Graaff.
Sarcinile electrice se acumulează pe cupola generatorului.
Dacă punem confeti, acestea se încarcă prin atingere cu sarcini de
acelaşi semn ca a generatorului şi vor fi respinse.
VIDEO (4)
28
29. Cum poţi măsura electrizarea unui corp? (faptul că este încărcat cu sarcină electrică)
Cel mai simplu instrument (aparat demăsură ) este ELECTROSCOPUL
Atingi corpul (C), despre care vrei să vezi
dacă este încărcat cu electricitate, de bila
electroscopului (E)
Să spunem că sarcina corpului (C) este
pozitivă (+). Atunci şi bila electroscopului
Electroscopul
(E) se încarcă cu pozitivă (+).
(E)
Sarcina se va scurge prin tija
electroscopului (E) către cele 2 lamele.
Acestea fiind încărcate cu sarcină de
acelaşi semn (+) în cazul nostru), se vor
respinge.
Cu cât sarcina e mai mare, cu atât forţa de respingere e mai mare.
Măsori respingerea şi poţi măsura sarcina.
(C
Corp
)
29
30. Continuare Cum poţi măsura electrizarea unui corp?
ExempluProfesorul stă pe un scaun (este astfel izolat de pământ).
Atinge Generatorul Van de Graaff (G.V.G.). Se încarcă astfel cu
electricitate (de acelaşi semn, dar acest lucru nu are importanţă acum).
Ţine în mână nişte fâşii de beteală metalică (acestea se încarcă şi ele cu
sarcină de acelaşi semn de la mână).
Fâşiile fiind încărcate cu sarcini de acelaşi semn se vor respinge.
Devine astfel un Electroscop viu.
La fel când îşi pune o perucă în cap.
Observaţie:
Încărcarea cu sarcină electrică nu este periculoasă dacă eşti izolat.
30
31. Electroscop
VIDEO (5)31
32. Cum obţii sarcină (+) sau (–) prin inducţie?
Ai un corp (C) încărcat cusarcină negativă (-) şi îl apropii
de 2 bile metalice care sunt în
Corp
(C)
1
2
contact.
Prin influenţă, pe faţa din stânga
a bilei 1 apare sarcină pozitivă
(+). Obligatoriu, pe faţa din
dreapta a bilei 2 apare sarcină
negativă (-).
Astfel se respectă legea conservării sarcinii
Pe ansamblu, dacă aduni sarcina pozitivă (+) de pe bila 1 cu sarcina
negativă (–) de pe bila 2, obţii 0, adică fără sarcină. Tot fără sarcină era şi
înainte de experiment.
32
33. Continuare Cum obţii sarcină (+) sau (–) prin inducţie?
Corp(C
)
1
2
Dezlipeşti cele 2 bile.
Sarcinile rămân blocate.
Sarcina pozitivă (+) pe sfera 1, iar sarcina negativă (–) pe sfera 2.
Pe ansamblu, sarcina totală nu se modifică, dar s-au obţinut sarcini
electrice pe cele 2 sfere în urma fenomenului de inducţie.
33
34. Cum demonstrezi că cele 2 bile au sarcini de semne diferite?
1)Te apropii cu corpul (C) (încărcat
iniţial cu sarcină pozitivă (+)) de
un electroscop (E).
Bila electroscopului are sarcină (-)
(de semn contrar cu a corpului (C)
pentru că te apropii, nu atingi şi
atunci e vorba de încărcare prin
inducţie, nu prin atingere).
Imediat foiţele electroscopului se
încarcă cu sarcină pozitivă (+) şi se
depărtează.
Corp
(C )
Electroscopul
(E )
34
35. Continuare Cum demonstrezi că cele 2 bile au sarcini de semne diferite?
2)Te apropii acum cu corpul (C)
încărcat cu sarcină negativă (-).
Prin apropiere, deci din nou prin
inducţie, bila electroscopului vrea să
se încarce cu sarcină pozitivă (+), iar
foiţele cu sarcină negativă (-).
Pe foiţe era de dinainte sarcină
pozitivă (+).
Prin urmare, sarcina pe foiţe rămâne
tot pozitivă (+) dar se micşorează şi
foiţele se apropie.
(C )
p
r
Co
Electroscopul
(E )
35
36. Separarea sarcinilor distribuite în urma fenomenului de inducţie electrică.
VIDEO (6)36
37. Alt exemplu de încărcare cu sarcini electrice prin inducţie electrostatică.
VIDEO (22)37
38. Concluzii care se desprind din film
1.Când 2 corpuri din materiale diferite vin în contact (de exemplu lâna
cu bumbacul) se realizează un transfer de electroni (e-) de la unul la
celălalt (bumbacul atrage e- ).
Astfel: lâna se încarcă cu sarcină pozitivă (+)
- (a pierdut e-)
bumbacul se încarcă cu sarcină negativă (–) - (a câştigat e-)
38
39. Continuare Concluzii care se desprind din film
Continuare2.
Concluzii care se desprind din film
Cel mai uşor mod de a neutraliza un corp încărcat cu sarcină electrică
este de a-l lega la pământ.
Dacă corpul este încărcat cu sarcină negativă (–)
e(are un surplus de e ), acesta va ceda pământului
e- şi va deveni neutru din punct de vedere electric.
Dacă corpul este încărcat cu sarcină pozitivă (+)
(are un deficit de e-), acesta va primi de la pământ
e- şi va deveni neutru din punct de vedere electric.
e-
39
40. Continuare Concluzii care se desprind din film
Continuare3.
Concluzii care se desprind din film
Numai ELECTRONII, sarcinile (-), se deplasează pentru că ei au
o masă mult mai mică decât PROTONII, sarcinile (+)
40
41. Incărcarea prin influenţă electrostatică
Considerăm un electroscop (E),neutru din punct de vedere
electric, care are numărul de
sarcini pozitive (+) egal cu
numărul de sarcini negative (-).
(Pentru
uşurinţa
explicării
fenomenului considerăm că are 7
sarcini pozitive (+) şi 7 sarcini
negative (-)).
Un corp (C) este încărcat cu
sarcini pozitive (+) (are un
surplus de sarcini pozitive (+), de
ex. 5).
Apropiem
corpul
(C)
de
electroscopul (E).
C)
(
p
r
Co
5 sarcini
Electroscopul (E) cu
7 sarcini
7 sarcini
41
42. Continuare Incărcarea prin influenţă electrostatică
3 sarciniCorp
( C)
5 sarcini
cei 7 e - s-au adunat pe bilă
aproape de corpul ( C)
Electroscopul (E) cu
7 sarcini
7 sarcini
dar altfel distribuite
foiţele au pierdut 4 e -,
rămân încărcate cu
şi se depărtează
Electronii din electroscopul (E) „simt” că există sarcini pozitive (+) pe
corpul (C) şi se „îngrămădesc” pe faţa bilei electroscopului, cât mai
aproape de (C). Această faţă devine (-).
Cealaltă faţă rămâne încărcată cu sarcini pozitive (+) pentru că a pierdut
3 e-.
La fel şi foiţele sunt încărcate cu sarcini pozitive (+) pentru că au pierdut
4 e-.
42
43. Primele concluzii la încărcarea prin influenţă
Pe ansamblul său, electroscopul este tot neutru din punct de vedere electric.Bila electroscopului este pe ansamblu negativă (sunt 7 sarcini negative (-) şi
doar 3 sarcini pozitive (+)).
Foiţele electroscopului sunt pozitive (câte 2 sarcini pozitive pe fiecare foiţă)
şi se resping.
Încărcarea prin influenţă înseamnă o
redistribuire de sarcini. Electroscopul (E) nu
a primit sau cedat sarcini, ci cele existente sau redistribuit
Corpul (C) nu păţeşte nimic, rămâne cum
era înainte, adică (+). El este doar cel care a
determinat, prin influenţă, redistribuirea
sarcinilor pe electroscop.
Dacă îndepărtez corpul (C), influenţa
dispare şi electroscopul revine la distribuţia
iniţială de sarcini şi foiţele se apropie pentru
că nu au sarcini.
(C
Corp
Electroscopul
(E)
neutru
43
)
44. Ce se întâmplă dacă leg tija electroscopului la pământ ?
Pământul, care e un rezervor imensde e-, sesizează că foiţele
electroscopului sunt încărcate cu
sarcini pozitive (+) şi trimite 4 epentru a le neutraliza.
În rest, cele 2 feţe ale bilei
electroscopului (E) şi corpul (C)
rămân cu aceleaşi sarcini ca mai
înainte.
Pe ansamblul său, electroscopul
(E) este încărcat cu sarcini negative
(-), pentru că avem numai 7 sarcini
(C )
p
r
Co
3 sarcini
Electroscop (E) cu
7 sarcini
11 sarcini
7 sarcini
4 e-
4 sarcini
4 sarcini
pozitive (+) şi 11 sarcini negative (-)
44
45. Ce se întâmplă
dacă deconectez pământ ?dacă depărtez corpul (C ) de bila
electroscopului?
Sarcinile de pe electroscopul
(E) se redispun ca în forma
iniţială.
Bila devine neutră (3 sarcini
pozitive (+) şi 3 sarcini
negative (-).
Foiţele devin (-) pentru că au
primit 4 e- şi acum sunt 8
sarcini negative (-) şi numai 4
sarcini pozitive (+). Foiţele se
vor depărta.
Per ansamblu, electroscopul
este încărcat cu sarcini
negative (-)
depărtăm corpul ( C)
redistribuirea sarcinilor
Corp (
C)
bila electroscopului
(E) este neutră:
3 sarcini
3 sarcini
deconectăm pământul
foiţele se încarcă ( )
şi se depărtează
4 sarcini
8 sarcini
Per ansamblu, Electroscopul (E) este negativ
45
46. Concluzii
Prin influenţă electrostatică şi apoi prin împământare încărcămelectroscopul (E) cu sarcină negativă (-), contrară sarcinii pozitive (+) a
corpului (C) care a determinat fenomenul de influenţă.
Sarcina negativă (-) de pe electroscopul (E) a provenit de la pământ.
Pământul este un izvor imens de sarcini negative (-).
Corpul (C) rămâne în starea sa iniţială de încărcare.
Poate fi folosit la infinit pentru a determina influenţa electrostatică şi
pentru alte corpuri conductoare.
46
47. Inducţia electrostatică. Experimente
După cum deja ştim, inducţia electrostatică constă în redistribuireasarcinilor electrice într-un corp sub acţiunea unei sarcini electrice
exterioare.
Un corp, neutru din punct de vedere electric, are un acelaşi număr de
sarcini pozitive şi negative, plasate apropiat unele de altele, astfel încât,
pe ansamblul său, corpul nu este încărcat electric (neutru din punct de
vedere electric)
Dacă corpul conductor (C.c.) este
plasat în vecinătatea unei sarcini
electrice produsă de un generator Van
de Graaff (G.V.G.) (de exemplu sarcină
negativă (-)) se realizează o redistribuire
corp conductor
neutru (C.c.)
a sarcinilor din corp.
Generator Van de Graaff
(G.V.G.)
47
48. Continuare Experimente
ContinuareAstfel, sarcinile pozitive (+) ale
corpului (C.c.) „vin” aproape de
sarcinile negative (-) ale
generatorului
(G.V.G.)
iar
sarcinile negative ale corpului
sunt respinse şi se concentrează
în direcţia opusă.
Pentru că inducţia electrostatică
este o simplă redistribuire de
sarcini, pe ansamblul său,
corpul rămâne neutru din punct
de vedere electric.
Inducţia
electrică
este
reversibilă: dacă dispare sarcina
care a produs efectul, dispare şi
redistribuirea sarcinilor.
Experimente
corp conductor
neutru (C.c.)
Generator Van de Graaff
(G.V.G.)
48
49. Încărcarea prin inducţie. 3 afirmaţii verificate experimental
1.Pe o faţă a unui corp conductor
neutru (C.c.), aflată mai aproape
de un generator Van de Graaff
(G.V.G). se acumulează sarcini
de semn contrar cu sarcina
G.V.G.
Avem un corp conductor, C.c.,
(neutru din punct de vedere
electric) pe care îl apropiem de
un G.V.G.
Pe faţa din dreapta (din
imediata vecinătate a G.V.G.)
corpul C.c acumulează un
surplus de sarcini pozitive (+)
de semn contrar cu cea a G.V.G.
corp conductor neutru
(Cc.) plasat aproape
de un G.V.G.
(G.V.G.)
49
50. Continuare Încărcarea prin inducţie. 3 afirmaţii verificate experimental
Continuare2.
3.
Încărcarea prin inducţie.
3 afirmaţii verificate experimental
Pe faţa aceluiaşi corp conductor (C.c.)
neutru, aflată mai departe de G.V.G.
se acumulează sarcini de acelaşi semn
cu sarcina G.V.G
Obligatoriu pe faţa din stânga
(depărtată de G.V.G ) apare un
surplus de sarcini negative (-)
Pe ansamblu, corpul conductor C.c.
rămâne neutru.
Sarcina se distribuie numai pe
suprafaţa exterioară a corpului
conductor.
În interior nu avem sarcină electrică
corp conductor
neutru (C.c.)
Generator Van de Graaff
(G.V.G.)
50
51.
Cum dovedim experimental corectitudinea celor 3 afirmaţii51
52. Afirmaţia 1
Pe o faţă a unui corp conductor C.c. neutru (cea care estemai apropiată de G.V.G.) se acumulează sarcini de un
semn contrar cu a G.V.G , adică (+) în cazul nostru
52
53. Afirmaţia 2
Pe cealaltă faţă a corpului conductor C.c. neutru (maidepărtată) se acumulează sarcini de acelaşi semn cu a
G.V.G, adică (-)
53
54. Demonstraţia afirmaţiilor 1 şi 2
Generatorul Van de Graaff, G.V.G, produce sarcini negative.Apropiem de generatorul G.V.G, un corp conductor C.c., neutru din punct de
vedere electric
Prin influenţă electrostatică sarcinile sunt distribuite astfel:
pe faţa din dreapta a C.c
(mai apropiată de generatorul
G.V.G,) se acumulează sarcini
pozitive (+)
pe faţa din stânga a C.c (mai
depărtată
de
generatorul
G.V.G.) se acumulează sarcini
negative (-)
bila (b), iniţial neutră,
prin atingere cu partea
stângă a corpului C.c
devine încărcată cu
sarcini (-)
corp conductor
neutru (C.c.)
Generator Van de Graaff
(G.V.G.)
Ating faţa din stângă a corpului conductor C.c. cu o bilă (b) neutră din punct de
vedere electric. Aceasta se încarcă cu sarcini negative (-)
54
55. Continuare Demonstraţia afirmaţiilor 1 şi 2
Apropii bila (b), acum încărcată cu sarcini negative (-), de un electroscop (E)Prin influenţă, sfera electroscopului
(E) se încarcă:
cu sarcini pozitive (+) pe faţa din
dreapta (de exemplu, 7 sarcini +)
cu sarcini negative (-) pe faţa din
stânga (de exemplu 3, sarcini ( -)
sfera
electroscopului este per
ansamblu pozitivă (+):
7 sarcini (+) însumate cu
3 sarcini (-) dau 4 sarcini (+)
cu sarcini negative (-) pe foiţe
(câte 2 sarcini negative (-) pe
fiecare foiţă (foiţele se resping)
7 sarcini
3 sarcini
Apropii bila (b)
de electroscopul (E)
Electroscopul
( E)
2 sarcini
2 sarcini
55
56. Continuare Demonstraţia afirmaţiilor 1 şi 2
Ating faţa din dreapta a corpului conductor C.c. cu o bilă (b) neutră dinpunct de vedere electric. Aceasta se încarcă cu sarcini pozitive (+)
corp conductor
neutru (C.c.)
bila (b), iniţial neutră,
prin atingere cu partea
dreaptă a corpului C.c
devine încărcată cu
sarcini (+)
Generator Van de Graaff
(G.V.G.)
56
57. Continuare Demonstraţia afirmaţiilor 1 şi 2
Apropii bila (b) acum încărcată cu sarcini pozitive (+), de electroscopul (E)pe faţa din dreapta a sferei
electroscopului (E) rămân 5
sarcini pozitive (+)
pe faţa din stânga sferei
electroscopului (E) rămân 3
sarcini negative (-)
pe
ansamblu,
sfera
electroscopului
(E)
este
pozitivă (+) (2 sarcini pozitive
(+) sunt anulate de 2 sarcini
negative (-) pe faţa din dreapta:
Apropii bila (b)
de electroscopul (E)
Electroscopul
( E)
57
58. Continuare Demonstraţia afirmaţiilor 1 şi 2
5 sarcini pozitive (+) de pe faţadin dreapta cu 3 sarcini (-) de pe
faţa din stânga fac ca sfera
electroscopului (E) să aibă un
surplus de 2 sarcini pozitive (+)
Foiţele au fiecare câte o sarcină
negativă (-), pe ansamblu
electroscopul (E) este neutru.
Foiţele se resping dar respingerea
este mai mică decât în cazul
demonstraţiei afirmaţiei 1
Apropii bila (b)
de electroscopul (E)
Electroscopul
( E)
58
59. Afirmaţia 3
Sarcina se distribuie numai pe suprafaţa exterioară acorpului conductor C.c., neutru din punct de vedere
electric. În interior nu avem sarcină electrică.
59
60. Demonstraţia afirmaţiei 3
Bila (b), neutră, o introducem în interiorul corpului C.c fără a atingepereţii acestuia
corp conductor
neutru (C.c.)
introducem bila (b),
iniţial neutră, în interiorul
corpului C.c, fără să
atingem pereţii acestuia
Generator Van de Graaff
(G.V.G.)
60
61. Continuare Demonstraţia afirmaţiei 3
Apropii, apoi, bila (b) de electroscopul E care este descărcat.Electroscopul (E)
descărcat
foiţele sunt apropiate
Nu se întâmplă nimic rezultând că:
bila (b) nu are sarcină;
bila (b) nu a preluat nici o sarcină atunci când a fost introdusă în
interiorul corpului conductor C.c
61
62. Sarcini prin inducţie
VIDEO (9)62
63. 1.5.3. Încărcarea unui corp conductor cu sarcini electrice prin ATINGERE
Dacă atingi un corp conductor încărcat electric de un alt corp conductorneîncărcat, acesta din urmă se încarcă local cu sarcină de acelaşi semn.
Considerăm un corp (C)
încărcat cu sarcini pozitive (+)
pe care îl atingem de un
electroscop (E), iniţial neutru
din punct de vedere al
încărcării
Sarcinile
negative
ale
electroscopului (e-) sunt atrase
de sarcinile (+) ale corpului şi
se transferă de pe (E) pe (C).
Corp ( C ) încărcat
cu sarcină ( )
Electroscopul (E)
neutru
-
63
64. Continuare Încărcarea unui corp conductor cu sarcini electrice prin ATINGERE
Corpul (C) avea suficiente sarcini pozitive (+) şi chiar dacă a primit (e-)rămâne (+).
Electroscopul a pierdut (e-) şi devine încărcat cu sarcini pozitive (+).
Foiţele sale se depărtează.
(
Corp
C)
Corpul ( C ), chiar dacă a primit e -, rămâne încărcat cu ( )
Electroscopul (E) pierzând sarcini ( ), (e-), devine încărcat cu ( )
Foiţele se vor depărta
64
65. Concluzie:
Prin ATINGERE Electroscopul (E) s-a încărcat cu sarcini de acelaşisemn cu cea a corpului (C), adică sarcini pozitive (+).
Numai ELECTRONII, sarcinile negative (-), se deplasează
65
66. Încărcarea prin ATINGERE şi prin INDUCŢIE. Experiment
Prin ATINGERE un corp conductor se încarcă cu sarcină de acelaşisemn.
Prin INDUCŢIE electrostatică la un corp conductor se realizează o
distribuţie de sarcini (pe ansamblul său corpul rămâne neutru din
punct de vedere electric)
66
67. Continuarea Încărcarea prin ATINGERE şi prin INDUCŢIE. Experiment
Avem un generator Van de Graaff care creează sarcini pozitive (+).Profesorul stă pe podea (neizolat faţă de aceasta). Electronii din
pământ sunt atraşi de sarcina pozitivă (+) a generatorului, urcă în corp
şi profesorul devine încărcat cu sarcină negativă (–) (aşa cum ştim deja,
prin inducţie electrostatică mă încarc cu sarcină de semn contrar
sarcinii (+) a generatorului, adică cu sarcină negativă (-)).
Atingem un balon metalic de generator. Prin atingere balonul se
încarcă cu sarcină de acelaşi semn, adică tot cu (+).
Balonul, încărcat cu sarcină pozitivă (+), va fi respins de sarcina (+) a
generatorului şi atras de sarcina negativă (-) a profesorului.
Când atinge capul profesorului, balonul se încarcă cu sarcină negativă
(-) şi este respins de sarcină negativă (-) cu care este încărcat profesorul
şi este atras acum de sarcina pozitivă (+) a generatorului. Prin atingere
cu acesta, balonul se încarcă din nou cu sarcină pozitivă (+) şi este
respins de sarcina pozitivă (+) a generatorul şi atras de sarcina negativă
(-) cu care este încărcat profesorul, şi ... acţiunea continuă la nesfârşit
67
68.
VIDEO (8)68
69. 1.6. Regimuri de funcţionare
Definiţie:Câmpul este acea formă de existenţă a materiei caracterizată printr-o
densitate foarte mică a acesteia şi capabilă să înmagazineze energie.
Din această definiţie, se disting două proprietăţi importante:
câmpul poate exista şi în afara materiei;
existenţa materiei atrage după sine şi existenţa unui câmp.
69
70. Continuare Regimuri de funcţionare
Câmpul electromagnetic, în ansamblul său, poate fi caracterizatprintr-un anumit număr de mărimi.
De exemplu,
starea unui câmp electrostatic în vid se caracterizează cu ajutorul unei
mărimi vectoriale de
stare, primitive, numită intensitatea câmpului
electrostatic în vid, E ,
E
iar în substanţă de perechea de mărimi vectoriale:
- intensitatea
câmpului electrostatic în substanţă şi D inducţia electrică (în
substanţă).
70
71. Continuare Regimuri de funcţionare
Aceste mărimi depind de:punct
şi sunt variabile în timp.
În spaţiul tridimensional, un punct este caracterizat de 3 mărimi care
reprezintă coordonatele corespunzătoare fiecărei axe, Ox, Oy, Oz.
Referitor la mărimea E, se poate scrie:
E(x, y, z) = variabil, care arată că ea depinde de punct
E(t ) = variabil,
care arată că depinde de timp.
71
72. Continuare Regimuri de funcţionare
În funcţie de modul în care variază mărimile de stare ale câmpului,regimurile de funcţionare se clasifică în:
1.
Regimul static în care:
mărimile de stare care caracterizează câmpul sunt invariabile în
timp;
E ( x, y, z ) var .,
E (t ) ct .
în interiorul câmpului nu are loc transfer de energie dintr-o formă
în alta;
între câmp şi exterior nu există transfer de energie.
72
73. Continuare Clasificare Regimuri de funcţionare
Continuare2.
Clasificare
Regimuri de funcţionare
Regimul staţionar în care:
mărimile de stare care caracterizează câmpul sunt variabile în
timp;
E ( x, y, z ) var .,
E (t ) var .
în interiorul câmpului are loc transfer de energie dintr-o formă în
alta;
între câmp şi exterior nu există transfer de energie.
73
74. Continuare Clasificare Regimuri de funcţionare
E ( x, y, z ) varlent., var iabil.,
Continuare
3.
EE
(t()t ) var
lent
. varia bil.
Clasificare Regimuri de funcţionare
Regimul cvasistaţionar în care:
mărimile de stare care caracterizează câmpul sunt lent variabile
în timp;
E ( x, y, z ) lent var iabil.,
E (t ) lent varia bil.
În interiorul câmpului are loc transfer de energie dintr-o formă în
alta;
Între câmp şi exterior există transfer de energie dar acesta este
mic ca amploare.
74
75. Continuare Clasificare Regimuri de funcţionare
Continuare4.
Clasificare Regimuri de funcţionare
Regimul nestaţionar în care:
mărimile de stare care caracterizează câmpul sunt variabile în
timp;
E ( x, y, z ) var .,
E (t ) var .
în interiorul câmpului are loc transfer de energie dintr-o formă în
alta;
între câmp şi exterior există un puternic transfer de energie.
75
76. 1.7. Stări de electrizare ale corpurilor
Definiţie:Starea în care se poate afla un corp asupra căruia se exercită acţiuni
mecanice atunci când este plasat într-un câmp electric se numeşte
stare de electrizare.
Corpurile pot fi aduse în starea de electrizare (pot fi electrizate) în
două moduri:
prin încărcare cu sarcină electrică adevărată q
(q - cantitatea de sarcină adevărată, care în Sistemul Internaţional
(SI) se măsoară în coulombi, C).
prin polarizare electrică, stare caracterizată prin mărimea
vectorială de stare numită polarizaţie electrică P şi care în SI se
măsoară în C/m2.
76
77. O primă întrebare
Cum adică, mă încarc cu electricitate dacă vin în contact cu un alt corpîncărcat cu electricitate ?
Da, corpul tău e un bun conducător de electricitate şi te vei încărca cu
sarcină electrică.
Şi ce fac,
mor ?
77
78.
Nu (.....acum).Ca să mori electrocutat trebuie să
treacă un curent prin tine, sarcinile
să circule prin tine. Dacă pui mâna
pe un obiect încărcat dar picioarele
stau pe un covor electroizolant,
corpul tău se încarcă cu electricitate
dar între tine şi pământ nu circulă
curent pentru că ai picioarele
izolate faţă de pământ.
Şi chiar nu păţesc nimic?
Ceva, ceva tot o să păţeşti...
Iată ...
78
79.
.….un mod simplu de a
înlocui şamponul
L’Oreal cu volum
Generatorul Van de Graaff poate crea o
mare cantitate de sarcini statice
(acumulează sarcini pe sferă).
Prin atingerea sferei corpul fetei se
încarcă cu sarcină. La fel şi părul.
Firele de păr, fiind încărcate cu
sarcină de acelaşi semn se vor
respinge.
79
80.
VIDEO (48)80
81. Ce este fulgerul ?
Fulgerul apare, tot din cauza existenţei sarcinilor electrice (de semnecontrare) ?
Este fulgerul periculos ?
Cum ne protejăm împotriva lui (ce facem în zilele cu furtună) ?
81
82. Fulgerul, trăsnetul şi tunetul
Fulgerul este un arc luminos rezultat în urma unui proces de descărcareelectrică cauzat de o diferenţă de potenţial electrostatic.
Acest fenomen meteorologic are loc în natură între nori încărcaţi cu
sarcini electrice diferite.
82
83. Continuare Fulgerul, trăsnetul şi tunetul
Descărcarea între nor şi pământ se numeşte trăsnet.Producerea unui fulger este urmată, la scurt timp, de apariţia tunetului, ce
reprezintă sunetul produs de descărcare.
Decalajul dintre observarea fulgerului şi receptarea sunetului, se datorează
diferenţei dintre vitezele de propagare ale celor două unde, luminoasă şi
acustică.
Descărcările electrice apar tot datorită existenţei unui câmp electric între nor
şi pământ.
La un moment dat sarcinile electrice
din nor străpung aerul şi se descarcă
(se deplasează) către sol.
Intensitatea
câmpului
E
şi
corespunzător şi tensiunea electrică
dintre nor şi pământ V au depăşit o
anumită
valoare,
numită
de
străpungere.
83
84. Oare la ce înălţime a fulgerat ?
Poţi calcula uşor dacă trăsnetul s-a produs, aproape de Pământ sau maideparte
Ai văzut fulgerul.
Pentru că lumina se deplasează cu o viteză foarte mare
v 3 108 m / s 300.000.000m / s 300.000 km / s 1.080.000.000 km / h
practic lumina ajunge instantaneu.
Începi să numeri până auzi trăsnetul (măsori timpul în secunde)
Pentru că sunetul se deplasează cu
v 340 m / s 1224 km / h
înmulţeşti timpul numărat cu 340 şi găseşti înălţimea unde s-a produs
trăsnetul (în m).
84
85. O energie fantastică care, deocamdată, nu poate fi înmagazinată
Un fulger călătoreşte cu viteza de 300.000km/s şi dezvoltă o temperatură de 28.000 C,
adică destul cât să topească orice fel de rocă
şi să o transforme în sticlă instantaneu. În
termeni uzuali, intensitatea curentului
provocat de fulger are, în medie, 40.000 A,
dar unele ajung chiar până la 120.000 A.
Energia unui astfel de fenomen e de cel
puţin 500 de megajouli, adică destul cât să
ţină aprins un bec de 100W timp de două
luni. Dar acesta este doar cel mai mic fulger
măsurat vreodată. Cercetătorii spun că
diferenţa de potenţial creată de un fulger
poate atinge 1 miliard de volţi.
85
86. Cum apar fulgerele?
Norii încărcaţi electric induc în pământul peste care trec o sarcinăelectrică egală şi de sens contrar.
„Electrizarea” suprafeţei solului face ca fulgerele să poată fi generate în
mai multe feluri:
de la nor la nor (când sunt încărcaţi cu sarcini diferite),
de la nor la pământ (şi atunci se numeşte trăsnet)
de la pământ spre nori.
Fulgerul care pleacă de la pământ spre nori se numeşte trăsnet
„pozitiv”, pentru că norul care îl provoacă are sarcinile pozitive spre
sol. În aceste cazuri, ce reprezintă numai 5% dintre toate fulgerele,
suprafaţa solului este încărcată negativ şi, cum descărcarea se produce
întotdeauna de la negativ spre pozitiv, fulgerul pleacă de la pământ
spre nor.
86
87. Întotdeauna oamenii fulgeraţi mor ?
Deşi e greu de crezut, având în vedere energiile colosale care sedezlănţuie în timpul unei descărcări electrice a norilor, 70% din
oamenii fulgeraţi supravieţuiesc şi 30% nu prezintă nici un semn vizibil
pe corp.
De câţiva ani există o organizaţie internaţională a oamenilor fulgeraţi
care au supravieţuit. Aceştia se întâlnesc în fiecare an în Tennessee şi
îşi povestesc unii altora experienţe incredibile pentru alţi oameni.
Sunt persoane care au fost fulgerate şi de câte zece ori, fiind un soi de
„magneţi umani pentru fulgere", dar oficial este recunoscut recordul
unui american din Florida, Tom Riverside, care a fost fulgerat de şapte
ori, de fiecare dată cu martori
87
88. Lecţii de Limba română
Om trăsnit: om care a fost lovit de trăsnet.Om trăznit: om mai neobişnuit, mai puţin formal, mai nebunatic.
88
89. Martin Luther, cel mai cunoscut fulgerat
Martin Luther, cel mai cunoscut fulgeratEvenimentul care i-a schimbat viaţa germanului ce avea să protesteze
vehement faţă de practicile Bisericii Catolice s-a produs lângă
localitatea Stotterheim, la 2 iulie 1505. Călugării luterani, care i-au scris
ulterior biografia, au notat că Martin avea atunci 22 de ani şi tocmai
terminase studiile de drept, la Universitatea din Erfurt. În ziua aceea se
întorcea de la părinţi, unde fusese în vizită, şi a fost surprins de furtună
în plin câmp, între satul Stotterheim şi oraşul Erfurt.
Călugării au notat că tânărul s-a rugat la Sfânta Ana să-l ferească de
fulgere şi i-a promis că se va călugări dacă ea îl va ajuta. Fulgerul, a
lovit chiar lângă Martin, iar el a fost atât de şocat de apropierea lui încât
n-a mai îndrăznit să nu-şi ţină legământul.
89
90. Continuare Martin Luther, cel mai cunoscut fulgerat
ContinuareMartin Luther, cel mai cunoscut fulgerat
Contemporanii laici ştiau însă altceva, după cum a notat chiar şi
Inchiziţia luându-le mărturiile. Fulgerul l-a lovit în plin pe tânărul
Luther, iar el a scăpat aparent nevătămat şi, din acel moment, a căpătat
percepţii speciale.
De altfel, e bine ştiut faptul că el singur spunea tuturor că Dumnezeu îi
vorbeşte, ceea ce, în viziunea inchizitorilor era o trufie demonică,
pentru că – după părerea lor – e evident că nimeni nu poate scăpa cu
viaţă dacă a fost fulgerat.
După două săptămâni s-a călugărit
90
91. Continuare Martin Luther, cel mai cunoscut fulgerat
ContinuareMartin Luther, cel mai cunoscut fulgerat
Martin a mers la Universitate, a dat o petrecere de despărţire şi pe 17
iulie 1505 a păşit peste pragul Mânăstirii Negre, din Erfurt, şi s-a
călugărit.
Acolo a rezistat în supunere numai până în anul 1517, când n-a mai
rezistat şi s-a apucat să scrie „ce ştia el de la Dumnezeu". În total au
fost 95 de reguli pentru creştini, pe care credincioşii le-au numit ulterior
„teze".
La 34 de ani, călugărul Martin Luther a încălcat dogma bisericii şi a
bătut pergamentul, în cuie, pe uşa bisericii din Wittenberg. A fost
primul gest al Reformei, iar Biserica Catolică l-a primit ca pe o palmă
peste faţă.
91
92. Cum protejăm clădirile împotriva trăsnetului
Paratrăsnetul este mijlocul prin care te poţi proteja împotriva loviturilorde trăsnet. Acesta este confecţionat din material conductor (are forma
unei săgeţi metalice), pusă pe un catarg destul de înalt pe clădire şi
legată printr-un conductor gros la o priză de pământ.
Vârful metalic atrage descărcarea de sarcini, se produce trăsnetul pe el
dar întreaga energie se scurge prin conductorul gros la pământ.
Casa este astfel protejată.
92
93. Cum ne protejăm noi împotriva trăsnetului?
Dacă eşti în oraş e puţin probabil să te lovească trăsnetul pentru cătoate clădirile au paratrăsnete. Ele atrag trăsnetul care cade pe ele şi tu,
care eşti pe stradă, nu păţeşti nimic.
Dacă eşti pe câmp deschis
Nu te adăposti sub copaci (aceşti sunt înalţi şi atrag trăsnetul chiar dacă nu sunt “metalici”)
Nu purta umbrelă (ea acţionează ca un paratrăsnet dar tu eşti legat
la umbrelă, şi eventualul trăsnet curge prin tine).
Deplasează-te cu paşi mici – nu fugi pentru că pot apare „tensiuni
de pas” şi te poţi electrocuta.
Despre „tensiunea de pas” vom vorbi altădată
Care e cel mai sigur mod de protecţie împotriva trăsnetului ?!
93
94.
Stai în casă şi înveţi !!94
95. Un “trăsnet” în laborator O descărcare în câmp.
Pe sferă s-au acumulat multe sarcinicare au creat un câmp puternic (foarte
intens) şi au „străpuns aerul” creând o
descărcare electrică.
95
96.
Video96
97. 1.8. Clasificarea corpurilor după modul în care se pot electriza
În funcţie de modul în care pot fi electrizate, corpurile se clasifică în3 categorii:
1.
Corpuri conductoare.
Un corp este conductor dacă este respins de un corp electrizat de
referinţă.
Corpurile conductoare se încarcă cu sarcină electrică adevărată q.
97
98. Continuare Clasificarea corpurilor după modul în care se pot electriza
Continuare2.
Clasificarea corpurilor după modul
în care se pot electriza
Corpuri izolatoare.
Un corp este izolator dacă este atras de un corp electrizat de
referinţă.
Corpurile izolatoare se pot încărca atât cu sarcină electrică
adevărată, cât şi cu sarcină de polarizaţie.
98
99. Continuare Clasificarea corpurilor după modul în care se pot electriza
Continuare3.
Clasificarea corpurilor după modul
în care se pot electriza
Corpuri semiconductoare.
Un corp este semiconductor dacă, în primă instanţă, este atras
apoi este puternic respins de un corp electrizat de referinţă.
99
100. 1.9. Legea conservării sarcinii electrice
Dacă se consideră un sistem de n corpuri aflate în stare electrizată şineelectrizată, conductoare, izolatoare şi semiconductoare, indiferent ce
se va petrece în acest sistem (contacte între corpuri, schimbarea
poziţiei lor relative cu condiţia să nu existe influenţe exterioare
sistemului, (sistemul este izolat) sarcina totală va rămâne riguros
constantă:
n
q
k
const.
k 1
Se poate afirma, deci, că producerea sau dispariţia unei sarcini electrice
este însoţită întotdeauna de producerea, respectiv dispariţia simultană,
pe acelaşi corp izolat, a unei sarcini egale de semn contrar.
100
101. Continuare Legea conservării sarcinii electrice
“Ţine minte” !!Legea conservării sarcinii provine dintr-o lege cu caracter cu totul şi cu
totul general, şi anume legea conservării substanţei şi energiei care
afirmă:
În Univers, nimic nu se pierde, nimic nu se câştigă ci totul se
transformă.
Totul în Univers există sub formă duală:
Electron (particulă electrică cu sarcină negativă e-) - Proton (particulă
electrică cu sarcină pozitivă e+).
Câmp electric – Câmp magnetic (Care împreună, în totalitatea sa
formează Câmpul electromagnetic).
Bine – Rău
Frumos – Urât
Dacă există ceva, trebuie să existe şi opusul său !
101
102. 1.10. Câmpul electrostatic în vid
Definiţie:Vidul este acea stare a substanţei (materiei) caracterizată printr-o
rarefiere extremă a acesteia
Observaţie:
Chiar dacă materia este puternic rarefiată, în vid poate exista câmp
După cum s-a precizat la clasificarea regimurilor de funcţionare,
câmpul electrostatic este un câmp electric care funcţionează într-un
regim static, adică mărimile care îl caracterizează sunt constante în
raport cu timpul.
102
103. Este spațiul cosmic un vid perfect ?
VIDEO (59)103
104. Continuare Câmpul electrostatic în vid
Proprietăţile electrice ale VIDULUI sunt caracterizate printr-o constantănumită permitivitate electrică a vidului, 0 care în SI (Sistemul
Internaţional) se măsoară în (farad / metru, unde faradul, F este unitatea
de măsură în SI pentru capacitatea electrică).
0 8,856 10 12
1
F / m
4 9 109
Existenţa câmpului electrostatic poate fi pusă în evidenţă experimental
prin forţa cu care acest câmp acţionează asupra unui corp electrizat.
Un corp este electrizat dacă este încărcat fie cu:
sarcină electrică adevărată,
fie polarizat electric
104
105.
Stai puţin să mă lămuresc !Deci în vid nu există masă ?
Dacă e “nimic” de ce mă interesează?
Da, vidul e “nimic”.
Pentru că el există şi orice există trebuie să ne intereseze.
Cum adică vidul poate înmagazina energie ?
Aceasta este cea mai frumoasă întrebare. Am putea “filozofa” zile
întregi.
DA, orice există (chiar dacă are masă sau nu are masă, adică e vid)
are proprietatea de a înmagazina energie.
105
106.
Nu-mi vine să cred !Dar energie?
Lucrurile pe care nu le văd nu înseamnă că nu există.
Vidul nu-l văd, dar există.
Ştiai că în Univers masă e doar 0.0000...1 % ? Adică puţină masă dar
mult vid?
Energie? O imensitate. Tot Universul înseamnă de fapt energie.
Dar corpul nostru, cum e ?
Corpul nostru......există..... deci înseamnă că acumulează energie.
Corpul nostru are masă.
Deci noi suntem masă şi energie.
106
107.
Pe scurt, pornind de la acest concept tratarea bolilor a cunoscut 2 direcţii:prima, prin medicina alopată (medicina clasică) care tratează
“masa” corpului uman,
cea de-a doua, medicina homeopată, tratează “energia” corpului
uman
Pentru că energia e mai “subtilă” e mai greu să o “vezi” şi deci să o
tratezi.
În trecut, medicina homeopatică era ramura cea mai dezvoltată - pentru că
industria medicamentelor (care tratează corpul, organul care te doare)
nu era aşa dezvoltată.
107
108.
Dar ce e Sufletul ?Sufletul e energia noastră.
El nu are masă, şi
poate să se acumuleze oriunde. În corpul nostru, sau apoi...
Un experiment foarte interesant, dar care nu a fost confirmat ştiinţific a
fost:
Un om a fost cântărit înainte de a muri şi apoi imediat după moarte.
Diferenţa a fost de 25,4 g. Adică sufletul, ca energie s-a acumulat în
aceste 25,4 g (el ar fi putut să se acumuleze şi în 0 g - dacă ştim că
sufletul există, adică este o formă de existenţă).
Ei, aceste 25,4 g pot circula prin Univers cu energia noastră (şi poate e
reconfortant să ştii că, totuşi, nu dispari “de
tot”.)
108
109. 1.11. Formula lui Coulomb
Se consideră două corpuri conductoare de dimensiuni neglijabile(sarcini punctiforme) încărcate cu sarcinile electrice adevărate q1, q2,
plasate în vid la distanţa r unul faţă de altul.
F12
F21
r
q1
q2
Forţele de interacţiune dintre
două sarcini punctiforme
Se numeşte vector de poziţie, r, vectorul care poate defini (preciza cu
exactitate) poziţia unui punct material în raport cu un sistem de
coordonate precizat.
109
110. Continuare Formula lui Coulomb
Dacă coordonatele unui punct în spaţiul tridimensional sunt (x, y, z)vectorul de poziţie poate fi exprimat ca:
r xi yj zk
y
unde:
i - se numeşte versorul axei Ox;
j
versorul axei Oy;
k
versorul axei Oz.
j
z
k
i
0
x
Sistem triotogonal de axe de
coordonate şi versorii acestuia
Definiţie:
Se numeşte versor vectorul care are modulul egal cu 1. Versorul arată
direcţia şi sensul mărimii vectoriale
110
111. Continuare Formula lui Coulomb
rr
Formula lui Coulomb
Continuare
r
Observaţie: Mărimea este un versor.
r
r
Într-adevăr, prelucrând obţinem:
r
r
xi yj zk
x
y
i
j
2
2
2
2
2
2
2
2
2
r
x y z
x y z
x y z
Este această mărime un vector?
Evident, da.
Are acest vector modulul egal cu 1?
x2 y 2 z 2
k
Modulul acestei mărimi este:
x
2
2
2
x y z
z
2
y
2
2
2
x y z
2
z
2
2
2
x y z
2
x2 y2 z 2
x2 y2 z 2
r
Prin urmare, mărimea este versorul r vectorului
r
1
111
112. Continuare Formula lui Coulomb
Formula lui CoulombContinuare
Formula lui Coulomb exprimă forţa de interacţiune dintre 2 sarcini
punctiforme ce se află la o distanţă r una faţă de alta şi sunt plasate în
vid (de permitivitate 0).
F
1
r
q1q2 3
4 0
r
0 8,856 10 12
1
F / m
9
4 9 10
Vectorul de poziţie:
Modulul vectorului de poziţie (distanţa dintre cele 2 sarcini)
r xi yj zk
r x2 y 2 z 2
112
113. Mici discuţii cu privire la Formula lui Coulomb
Dacă există 2 sarcini între ele apare o forţă.Forţa e mare dacă sarcinile au valoare mare
Forţa e mare dacă sarcinile sunt apropiate (distanţa e mică).
Dacă sarcinile sunt de acelaşi semn (ambele pozitive sau ambele
negative) forţa e de respingere.
Dacă vrei să exprimi forţa ca modul (atenţie că în formula generală e
vector) obţii:
F
1
1
q1q2 2 1 2 2
4 0
r
4 0 r
113
114. Continuare Mici discuţii cu privire la Formula lui Coulomb
Puţină “filozofie” nu strică !!Ştiai că la nivelul maselor (a corpurilor care au o masă) există o formulă
asemănătoare numită legea atracţiei universale ?
F k
m1m2
r2
k este constanta de atracţie ;
k 6,7 10 11
114
115. Continuare Formula lui Coulomb
De ce această formulă nu are vectori? E doar în modul (un scalar) ?În formula lui Coulomb apar vectori pentru că forţa poate fi, fie de atracţie
(sarcini de semne contrare), fie de respingere (sarcini de acelaşi semn).
Vectorul ne arată:
orientarea forţei şi,
Pământ
Lună
valoarea (mărimea) sa.
F
F
m2
m1
r
Forţa de atracţie universală între Pământ şi Lună.
Faptul că cele două forţe sunt egale şi de semne contrare respectă legea
acţiunii şi reacţiunii
În legea atracţiei universale, e clar că, forţa este de atracţie şi atunci nu
avem nevoie de un vector ci de un scalar.
Scalarul ne arată doar:
mm
valoarea (mărimea) sa F k 1 2 2
r
115
116. Continuare Formula lui Coulomb
M-am prins !!Legea atracţiei universale spune că 2 corpuri se atrag.
Cu cât distanţa e mai mică cu atât forţa e mai mare.
Abia acum înţeleg eu de ce sunt “atras”
de prietena mea !!
E o lege a Universului căreia nu mă pot opune !!
Acum îmi mai explic o lege !! Şi am să o ţin minte
Legea acţiunii şi reacţiunii:
Dacă un corp acţionează asupra altui corp cu o forţă F, cel de-al doilea
acţionează asupra primului cu o forţă egală, dar de sens contrar
116
117. Înaintea mea a fost Isaac Newton (cel mai mare om de ştiinţă a lumii)
VIDEO min 5.50117
118. Comparaţie între
forţa electrostaticăFe
şi
forţa de atracţie universală
1
1
q1q2 2 ke 1 2 2 9 109 1 2 2
4 0
r
r
r
Fa k
m1m2
11 m1m2
6
,
7
10
r2
r2
Dacă calculăm aceste 2 forţe pentru 2 protoni valorile numerice sunt:
Fe 9 10
9
1,6 10
19 2
Fa 6,7 10
r2
q1 q2 1,6 10 19
Fe 1036 Fa
11
1,7 10
27 2
r2
m1 m2 1,7 10 27
Aşadar, forţa de respingere electrostatică dintre 2 protoni Fe este de 1036 ori
mai mare decât forţa de atracţie universală dintre ei Fa.
118
119.
Atunci, cum de nu „explodează” nucleu, atomul dacă respingerea esteatât de mare?
La nivel atomic (distanţe foarte mici) mai există o forţă şi anume forţa
nucleară care este de atracţie. Ea este cu mult mai mare decât cea
electrostatică şi „ţine” atomul să nu se dezintegreze.
Există 4 forţe în Univers:
Forţa nucleară (care este dominantă pentru distanţe foarte mici între
corpuri, de ordinul 10-20 m). Ea ţine atomul „să nu se împrăştie”;
Forţa nucleară slabă (care este dominantă pentru distanţe tot foarte
mici 10-20 m). Cu ajutorul ei atomii se pot „sparge”.
Forţa electromagnetică (care este dominantă pentru distanţe mici
între corpuri, de ordinul cm şi m).
Forţa newtoniană (forţa de atracţie universală) (care este dominantă
pentru distanţe foarte mari între corpuri, de ordinul 1020 m şi mai
mari).
119
120. Cele mai mari descoperiri
VIDEOCD 100 cele mai
mari descoperiri
min40
120
121. 1.12. Corp de probă
Studiul câmpului electrostatic se realizează experimental prin tatonareacâmpului cu ajutorul unui corp de probă.
A tatona un câmp înseamnă a determina forţa, eventual cuplul, cu care
câmpul acţionează asupra unui corp plasat în diferite puncte ale sale.
Se consideră o sarcină electrică q care
creează un câmp. Teoretic, câmpul
creat de această sarcină este infinit,
însă, la distanţe foarte mari
intensitatea sa este foarte mică şi
poate fi neglijată. Astfel, se poate
delimita un volum V în care câmpul
acţionează .
F1
A
q0
r1
q
corp încărcat cu
sarcină care creează
un câmp electric
r2
q0
B
F2
Tatonarea unui câmp cu ajutorul
corpului de probă de sarcină q0
121
122. Continuare Corp de probă
Prin tatonarea volumului V cu ajutorul corpului de probă , într-omultitudine de puncte, se poate determina în aceste puncte valoarea
forţei cu care câmpul acţionează asupra corpului de probă.
Se pot astfel obţine informaţii cu privire la câmpul respectiv.
Pentru ca un corp să fie considerat corp de probă, el trebuie să
îndeplinească următoarele condiţii:
Să aibă o dimensiune suficient de mică (teoretic – punctiform).
Sarcina cu care este încărcat trebuie să fie invariabilă în timp.
Prin introducerea corpului de probă în câmp, acesta nu trebuie să
influenţeze structura câmpului.
Concluzie:
O sferă de rază foarte mică, confecţionată dintr-un material conductor,
poate fi considerată ca fiind un corp de probă.
122
123. 1.13. Intensitatea câmpului electrostatic în vid
Consider o sarcină q1Această sarcină creează în vid, la o distanţă r
un câmp electric de o intensitate E.
q1 r
E
4 0 r 3
Dacă plasez o altă sarcină q în acest asupra sa
se va exercita o forţă F
F 1
4 0
F
q
r
q1
r
r3
123
124. Continuare Intensitatea câmpului electrostatic în vid
Relaţia dintreE
şi
F
q1q r
F
4 0 r 3
q1 r
E
4 0 r 3
F1 qE1
F - se măsoară în Newtoni (N)
E - se măsoară în Newtoni / Coulombi (N/C ) sau în Volt / metru (V/m)
q - se măsoară în Coulombi (C)
r - se măsoară în metri ( m )
124
125. Despre intensitatea câmpului E
EDespre intensitatea câmpului E
În general, E are componente după toate cele trei direcţii:
E Ex i E y j Ez k
În funcţie de componentele sale după cele trei direcţii Ex, Ey, Ez ,
modulul intensităţii câmpului se calculează cu relaţia:
E Ex2 E y2 Ez2
125
126. Puţină recapitulare !
Orice corp încărcat cu sarcină creează un câmp electric?Da
Dacă pun un alt corp încărcat cu sarcină în acest câmp asupra lui se
exercită o forţă ?
Da
Cât de mare e această forţă ?
La nivel macroscopic (la nivelul corpurilor care ne înconjoară) forţa
aceasta e foarte mică, dar la nivel microscopic are valori care „se
simt”.
„Cât de mari sunt sarcinile acestea” ?
Dacă vorbim de sarcinile elementare de exemplu electronul, acesta
are:
masa m 9,1 10 31 kg
sarcina electrică e 1,6 10 19 C
se deplasează cu viteze de ordinul vitezei luminii care este
c 3 108 m / s
126
127. Continuare Puţină recapitulare !
Cum este orientat vectorul E ?Vectorul E
E
“iese” din sarcina pozitivă
E
“intră“ în sarcina negativă
127
128. Continuare Puţină recapitulare !
Cum arată câmpul electric creat de 2 sarcini ?Câmpul creat de 2 sarcini pozitive (+) (sensul
liniilor de câmp ies din sarcini)
Câmpul creat de 2 sarcini de semne contrare:
sensul liniilor de câmp ies din sarcina
pozitivă (+),
şi intră în sarcina negativă (-)
Săgeţile arată cum s-ar deplasa o sarcină pozitivă (+) plasată în câmp
(aceasta se deplasează în sensul liniilor de câmp).
128
129. Linii de câmp
VIDEO (7)129
130. Exerciţiu
Care este figura în care liniile de câmp sunt reprezentate corect,pentru 2 protoni şi 1 electron ?
130
131. Răspuns
Liniile de câmp trebuie:1.
să iasă din sarcina pozitivă (+);
2. să intre în sarcina negativă (-);
3. pentru că sarcinile sunt apropiate, fiecare din cele 3 câmpuri se
influenţează unul pe celălalt şi liniile de câmp nu mai sunt radiale
(drepte) ci curbe.
Liniile de câmp sunt reprezentate corect în figura d )
131
132. Puţin despre corpul nostru
În corpul uman, absolut toată activitatea, viaţa, funcţionalitatea sa sebazează pe legile fizicii.
Nu corpul uman a învăţat legile ci noi am reuşit să le descoperim,
învăţând astfel cum funcţionează el.
Inima funcţionează pe baza a 4 pompe electrostatice,
1. cea de sodiu (Na)
2. cea de potasiu (K)
3. cea de calciu (Ca)
4. cea de magneziu (Mg).
Datorită unor diferenţe de potenţial (tensiune electrică) anionii (sarcini
negative (-)) şi cationii (sarcini pozitive (+)) pot străbate membranele
celulare într-un sens şi celălalt.
Curenţi electrici comandă funcţionarea oricărui muşchi.
Vedem datorită unor impulsuri electrice transmise creierului.
132
133. 1.14. Linii de câmp în câmpul electrostatic
DefiniţieSe numeşte linie de câmp în câmpul electrostatic curba tangentă în
orice punct la vectorul .
E1
Ecuaţia liniilor de câmp este:
E dl 0
E3
E2
Linii de câmp în câmp electrostatic
Observaţii:
reprezintă elementul infinitezimal al dreptei l care se mai numeşte şi
element de lungime. Scris în funcţie de coordonatele după cele 3
direcţii, acesta are expresia:
dl dxi dyj dzk
E are expresia
E Ex i E y j Ez k
133
134. Continuare Linii de câmp în câmpul electrostatic
Ce înseamnă şi cum se efectuează un produs vectorial ?Un produs vectorial efectuat în funcţie de componentele sale după cele
3 direcţii se calculează cu expresia:
i
j
E dl 0 E x
Ey
dx
dy
k
Ez 0
dz
i E y dz Ez dy j Ez dx Ex dz k Ex dy E y dx 0
În urma efectuării unui produs vectorial rezultă un vector.
134
135. Continuare Linii de câmp în câmpul electrostatic
Ce înseamnă şi cum se efectuează un produs scalar ?Un produs scalar efectuat în funcţie de componentele sale după cele 3
direcţii se calculează cu expresia:
E dl Ex dx E y dy Ez dz
Ecuaţia liniilor de câmp
Prelucrând expresia ecuaţiei liniilor de câmp ,
ecuaţia liniilor de câmp în câmpul electrostatic:
E dl 0
se obţine
dx dy dz
Ex E y Ez
135
136. Continuare Linii de câmp în câmpul electrostatic
Cum arată liniile de câmp ?linii de câmp
Dacă ar fi o singură sarcină, liniile de câmp ar fi
cercuri având centrul în sarcină.
Dacă 2 sarcini sunt plasate apropiat, fiecare îşi
creează propriul câmp şi câmpul rezultant este
suprapunerea celor 2 câmpuri. De aceea cercurile nu
mai au centrul în sarcini.
sarcină electrică
pozitivă (+) sau
negativă (-)
+
136
137. 1.15. Densităţi de sarcină
Sarcina electrică q este o mărime primitivă, care caracterizează stareade încărcare electrică a corpului.
Aceasta se poate distribui:
Punctiform
Liniar
Superficial
Volumetric
Exemple:
Un fir conductor foarte subţire, încărcat cu q, are
sarcina distribuită liniar;
Un corp de grosime foarte mică are sarcina
distribuită superficial ;
Un corp de un anumit volum poate avea sarcina
distribuită volumetric.
l
dl
l
S
dA
S
dV
V
V
137
138. 1.15.1. Densitate liniară de sarcină l
1.15.1. Densitate liniară de sarcină lConductoarele lungi şi foarte subţiri se încarcă cu sarcină distribuită
lineic (filiform) cu densitatea lineică de sarcină l
dq
q
l
lim
dl l 0 l
dl
l
de unde rezultă:
dq l dl
l
q l l dl
În Sistemul internaţional (SI) densitatea liniară de sarcină se măsoară
în C/m.
138
139. 1.15.2. Densitate superficială de sarcină S
1.15.2. Densitate superficială de sarcină SConductoarele de grosime mică şi suprafaţă mare se încarcă cu sarcină
distribuită superficial cu densitatea superficială de sarcină S
dq
q
S
lim
dA A 0 A
dA
S
de unde rezultă
dq S dA
S
q S dA
S
În SI, densitatea superficială de sarcină se măsoară în C/m2
139
140. 1.15.3. Densitate volumetrică de sarcină V
1.15.3. Densitate volumetrică de sarcină VCorpurile izolatoare (dielectricii) de grosime şi suprafaţă mare se
încarcă cu sarcină distribuită volumetrică cu densitatea volumetrică de
sarcină V
V
dq
q
lim
dV V 0 V
dV
V
V
de unde rezultă:
dq V dV
q V dV
V
În SI densitatea volumetrică de sarcină se măsoară în C/m3
140
141. Continuare Densitate volumetrică de sarcină V
ContinuareDensitate volumetrică de sarcină V
Observaţii:
Corpurile conductoare care ocupă un anumit volum se încarcă,
întotdeauna, cu sarcină distribuită superficial (sarcina se distribuie
numai pe suprafaţa acestora cu o densitate superficială de sarcină).
sarcina electric nu se distribuie în
tot volumul corpului conductor ci
numai pe suprafaţa sa exterioară
(cu densitate S )
S
V
Corpurile izolatoare care ocupă un anumit volum se pot încărca cu
sarcină distribuită superficial sau volumetric.
sau
S
V
V
V
La un corp izolator sarcina se poate distribui
fie superficial (cu S ) fie volumetric cu (
V
141
142. 1.16. Descărcarea electrostatică
De ce apar scântei când un corp este încărcat electrostatic ?Descărcarea electrostatică reprezintă curentul electric (instantaneu şi
temporar) care ia naştere între 2 corpuri, între care nu există legătură
electrică (adică separate de aer), aflate la potenţiale diferite.
Descărcarea se manifestă vizual sub forma unei scântei şi auditiv sub
forma unei mici pocnituri.
Scânteia poate provoca explozii dacă mediul este inflamabil sau
explozibil.
Cauza apariţiei descărcării electrostatice o reprezintă existenţa
electricităţii statice.
142
143.
VIDEO (10)143
144. Descărcător static montat pe aripile avioanelor
Întreeventualele
sarcini
electrice
acumulate şi vârfurile metalice apar
scântei.
Vârfurile metalice au o “colivie” de plastic
protectoare care face ca scânteia să nu se
transmită alăturat.
144
145. Filtru electrostatic
Unfiltru
electrostatic
este
confecţionat din fibre capabile să se
încarce electrostatic şi să păstreze
sarcina pe ele. Această sarcină
atrage particulele de praf, polen,
etc. care se depun pe filtru.
145
146. Ce înseamnă încărcare electrostatică ?
Dacă un corp acumulează sarcini electrice înseamnă că s-a încărcatelectrostatic (sarcinile electrice nu „circulă” pe suprafaţa corpului
respectiv).
Corpurile sintetice (de plastic) pot acumula sarcini prin frecare.
Electricitatea statică poate apare prin:
Frecare
Fenomenul de inducţie electrostatică
Corpurile conductoare nu pot acumula sarcini prin frecare.
146
147.
O scânteie electrică provenităde la o acumulare electrostatică
poate provoca explozie într-un
mediu inflamabil !
147
148.
Dirijabilul Hindenburg distrus deo explozie din cauza apariţiei unei
scântei cauzată de acumularea de
sarcini electrice statice.
Apariţia
unei
descărcări
electrostatice se manifestă printr-o
scânteie electrică.
Dacă mediul este inflamabil
această scânteie poate crea o
explozie.
Balonul trecuse printr-o furtună şi se acumulase pe el o mare sarcină
electrică. Când au fost aruncate odgoanele metalice pentru aterizare, a
apărut o scânteie între odgon şi turnul metalic care a dus la explozia
hidrogenului din balon
148
149. Explozii datorate încărcărilor electrostatice
În 1989 un tun de pe un vas de luptă a explodat.Cauza: încărcarea electrostatică care, prin declanşarea unei scântei, a
detonat încărcătura explozivă
149
150.
VIDEO (38)150
151. Ce facem pentru evitarea apariţiei încărcărilor electrostatice?
Toate corpurile se leagă la pământ cu cordoane electrice.Astfel, sarcinile electrice sunt scurse la pământ şi nu se mai pot
acumula pe corpurile respective
151
152. Dar de ce se poate livra benzină la canistre metalice?
Suprafaţa corpurilor conductoare este o suprafaţă echipotenţială (toatepunctele au acelaşi potenţial).
Sarcinile electrice nu se pot acumula pe suprafeţe mici (ale aceleiaşi
suprafeţe mare conductoare).
De aceea nu poate apărea scânteia electrică.
152
153. Puţină recapitulare a unor mărimi şi fenomene învăţate
1.Ce înseamnă că pH-ul apei este 7?
Înseamnă că 1 din 107 molecule este ionizată, adică molecula
conţine ionul negativ HO- şi ionul pozitiv H+.
Orice pH ar avea apa, tot există unele molecule ionizate care se
comportă ca nişte sarcini electrice.
153
154. O baterie electrică extraordinară. Picurătorul lui Kelvin
VIDEO (19)154
155. Continuare Puţină recapitulare a unor mărimi şi fenomene învăţate
Continuare2.
Puţină recapitulare a unor mărimi şi
fenomene învăţate
Ce înseamnă încărcare a unui corp prin inducţie electrică (influenţă
electrostatică)?
Dacă ai un corp conductor 1 neutru din punct de vedere electric şi
îl apropii de un corp 2 încărcat cu sarcină (de exemplu (+)), pe
corpul 1 sarcinile se distribuie:
Pe porţiunea corpului 1 aflată mai aproape de 2 apare sarcină de
semn contrar cu 2, adică (–).
Pe porţiunea corpului 1 aflată mai departe de 2 apare sarcină de
acelaşi semn cu 2, adică (+).
155
156. Continuare Puţină recapitulare a unor mărimi şi fenomene învăţate
Continuare3.
Puţină recapitulare a unor mărimi şi
fenomene învăţate
Cum pot apare sarcini electrice pe un corp conductor?
Prin INDUCŢIE ELECTRICĂ.
Dacă apropii un corp încărcat electric de un corp conductor
neîncărcat, acesta din urmă se încarcă local cu sarcină de semn
contrar
Corpul ce se încarcă prin INDUCŢIE
Dacă a apărut o
sarcină ( ),
obligatoriu apare
şi o sarcină ( )
Astfel, pe ansamblu,
corpul rămâne neutru,
aşa cu era iniţial
Pentru că
sarcinile ( ) ale
corpului ( C )
atrag sarcinile ( ) ,
sarcina distribuită
local este ( )
Corp ( C ) încărcat
cu sarcină ( )
156
157. Continuare Puţină recapitulare a unor mărimi şi fenomene învăţate
Continuare4)
Puţină recapitulare a unor mărimi şi
fenomene învăţate
Ce însemnă intensitate de străpungere?
Orice corp izolator nu este perfect, adică se străpunge dacă
intensitatea câmpului electric depăşeşte o anumită valoare.
Aerul este un izolator.
Intensitatea câmpului la care aerul se străpunge este:
Estrăpungere aer 3 106 V / m
157
158. Continuare Puţină recapitulare a unor mărimi şi fenomene învăţate
Continuare5.
Puţină recapitulare a unor mărimi şi
fenomene învăţate
Ce însemnă tensiune de străpungere (când apare descărcarea prin
scânteie)?
Considerăm că avem 2 corpuri plasate în aer la distanţa d.
Între acestea tensiunea este U.
Intensitatea câmpul dintre corpuri este E.
Ştim relaţia: E=U/d . Asta înseamnă că:
U străungere aer 3 106 V
dacă
d 1m
U străungere aer 3 105 V
dacă
d 0,1m
U străungere aer 3 10 4 V
dacă
d 0,01m
Când s-a depăşit U străpungere între cele 2 corpuri apare o
descărcare prin scânteie (apare un curent electric de foarte scurtă
durată care egalizează potenţialele celor 2 corpuri).
158
159. Continuare Puţină recapitulare a unor mărimi şi fenomene învăţate
Continuare6.
Puţină recapitulare a unor mărimi şi
fenomene învăţate
Cum se deplasează sarcinile electrice în câmp?
Sarcinile pozitive (+) circulă în sensul liniilor de câmp.
Sarcinile negative (-) circulă în sens invers
Ştim că 2 sarcini de acelaşi semn se
resping.
Pentru că la sarcina pozitivă liniile
de câmp ies din sarcină, e clar că q+
se deplasează în sensul liniilor de
câmp.
E
F
159
160. 1.17. Teorema suprapunerii efectelor referitor la intensitatea câmpului electrostatic
Se consideră că într-un punct din spaţiu se află o sarcină q care esteplasată în câmpurile create de alte sarcini q1, ..., qn.
Se notează cu vectorii de poziţie.
Forţa rezultantă care acţionează în punctul în care se află sarcina q se
determină prin aplicarea teoremei suprapunerii efectelor referitor la
forţe.
F F1 Fn
n
Fi
i 1
Expresia matematică a teoremei suprapunerii efectelor referitor la
intensitatea câmpului electrostatic este
E
n
Ei
i 1
160
161. Continuare Teorema suprapunerii efectelor referitor la intensitatea câmpului electrostatic
Observaţii1.
Teorema suprapunerii efectelor referitor la intensitatea câmpului
electrostatic are aceeaşi formă ca cea referitoare la suprapunerea
forţelor şi se enunţă astfel:
Intensitatea rezultantă a unui câmp electrostatic creat de o
distribuţie continuă şi discretă de sarcini este egală cu suma
vectorială a intensităţilor create de fiecare distribuţie în parte.
161
162. Continuare Teorema suprapunerii efectelor referitor la intensitatea câmpului electrostatic
Ce înseamnă distribuţie continuă şi distribuţie discretă de sarcini ?Dacă sarcina se distribuie lineic, superficial sau volumetric se
spune că are o distribuţie continuă.
Dacă sarcina se distribuie punctiform se spune că are o distribuţie
discretă (se poate număra).
Practic cuvintele distribuţie continuă şi discretă de sarcini acoperă
toate modurile în care se poate distribui o sarcină electrică.
162
163.
Mai ţii minte că o sarcină electrică se poate distribui în 4 moduri ?1.
2.
3.
4.
Punctiform
Lineic
Superficial
Volumetric
163
164. 1.18. Forma generală a intensităţii câmpului electrostatic
Se consideră că, într-un volum oarecare din spaţiu, se află:o sarcină distribuită pe un conductor de
lungime l cu densitate liniară de sarcină
l;
o sarcină uniform distribuită pe o
suprafaţă S cu densitatea superficială de
sarcină, S.
o sarcină uniform distribuită într-un
volum V cu densitatea volumetrică de
sarcină, V .
n sarcini punctiforme
dl
l
r
l
P
r
S
dA
ri
r
S
dV
V
qi
V
Se urmăreşte determinarea intensităţii câmpului într-un punct P din acest
spaţiu, identificat în raport cu sarcinile prin vectorii de poziţie r (evident
aceştia sunt diferiţi între ei, însă, pentru uşurinţa scrierii, nu s-au folosit
indici).
164
165. Intensitatea câmpului electrostatic în vid creat de diferite distribuţii de sarcini
1.Intensitatea câmpului creat de sarcina distribuită liniar este:
El
1
4 0
l dl r
l
r3
165
166. Continuare Intensitatea câmpului electrostatic în vid creat de diferite distribuţii de sarcini
Continuare2.
Intensitatea câmpului electrostatic în
vid creat de diferite distribuţii de sarcini
Intensitatea câmpului creat de sarcina distribuită superficial este:
ES
1
4 0
S dA r
S
r3
166
167. Continuare Intensitatea câmpului electrostatic în vid creat de diferite distribuţii de sarcini
Continuare3.
Intensitatea câmpului electrostatic în
vid creat de diferite distribuţii de sarcini
Intensitatea câmpului creat de sarcina distribuită volumetric este:
1
EV
4 0
V dV r
V
r3
167
168. Continuare Intensitatea câmpului electrostatic în vid creat de diferite distribuţii de sarcini
Continuare4.
Intensitatea câmpului electrostatic în
vid creat de diferite distribuţii de sarcini
Intensitatea câmpului creat de o sarcină distribuită punctiform este:
E
1
4 0
n
i 1
qi ri
ri3
168
169. Continuare Intensitatea câmpului electrostatic în vid creat de diferite distribuţii de sarcini
Aplicând teorema suprapunerii efectelor se obţine expresia intensităţiicâmpului electrostatic în vid:
1 l dl r
Erez
l 3
4 0
r
S dA r
3
S
r
V dVr
3
V
r
n
i 1
qi ri
ri3
169
170. Avem nevoie de ceva matematică !!
Se introduc următorii operatori matematici utili în studiul câmpuluielectromagnetic:
Gradientul
(grad)
Gradient – grad: este un operator matematic care se aplică unui scalar
şi are ca efect obţinerea unui vector.
Exemplu: prin aplicarea operatorului gradient unui scalar V se obţine
un vector M :
grad V M
M M xi M y j M z k
Mx, My, Mz – se obţin prin derivarea scalarului după cele 3 direcţii
V
V
V
V V V
Mx
; My
; Mz
;
M grad V
i
j
k
prin
urmare:
x
y
z
x
y
z
170
171. Continuare Avem nevoie de ceva matematică !! Ce înseamnă grad mai pe înţelesul nostru ?
1.Ce înseamnă grad ?
Înseamnă derivare parţială după cele 3 direcţii, Ox, Oy şi Oz.
171
172. Continuare Avem nevoie de ceva matematică !!
Continuare2.
Avem nevoie de ceva matematică !!
Ce înseamnă derivare parţială (după axa Ox)?
Înseamnă variaţia mărimii (ΔV) împărţită la variaţia variabilei (Δx)
dacă faci variaţia după axa Ox : V V ;
dacă ai face variaţia după axa Oy ai pune Δy, etc.
x
x
Adică arată cât creşte (sau scade) mărimea respectivă după axa Ox ,
Oy sau Oz .
172
173. Continuare Avem nevoie de ceva matematică !!
Continuare3.
Avem nevoie de ceva matematică !!
Dă-mi un exemplu !
Dacă V are valoarea V1 = 7 în punctul x 1 = 3 şi valoare V2 = 17 în
punctul x 2 = 5 atunci gradientul după axa Ox este:
grad V
V 17 7 10
i
i i 5i
x
5 3
2
173
174. Continuare Avem nevoie de ceva matematică !!
Continuare4.
Avem nevoie de ceva matematică !!
Dar dacă ar fi să îl calculezi după cele 3 direcţii?
Să spunem că după Ox a ieşit 5, după Oy a ieşit 9 şi după Oz a
ieşit - 4 atunci, aplicând formula gradientului obţii:
grad V 5i 9 j 4k
174
175. Continuare Avem nevoie de ceva matematică !!
Continuare5.
Avem nevoie de ceva matematică !!
Văd eu bine că am obţinut un vector (îl recunosc uşor după versorii
i , j şi k )?
Da, dacă aplici operatorul gradient, obţii ca rezultat un vector.
175
176. Continuare Avem nevoie de ceva matematică !!
Cui se aplică operatorul gradient?Obligatoriu unui scalar
176
177.
Ai auzit cuvântul gradient la rubrica meteo,unde se spune „gradientul temperaturii
este mare şi pozitiv dacă ne deplasăm de
la vest la est”.
Acest lucru înseamnă că temperatura în vest
e mai mare decât în est (gradientul e
pozitiv) şi scade repede (pentru că
gradientul e mare).
În concluzie, gradient înseamnă variaţia
mărimii (dintr-un punct în altul)
împărţită la distanţa dintre puncte.
177
178. Continuare Avem nevoie de ceva matematică !!
Avem nevoie de ceva matematică !!Continuare
Rotorul (rot)
Rotor – rot : este un operator matematic care se aplică întotdeauna unui
vector şi are ca efect obţinerea tot a unui vector.
Exemplu: prin aplicarea operatorului rotor
vectorul
R calculat cu expresia
i
R rot P
x
Px
j
y
Py
unui vector P se obţine
k
z
Pz
P
P
P
P
P
P
z y i x z j y x k
y
x
z
z
x
y
Ry
R
R
x
z
178
179. Continuare Avem nevoie de ceva matematică !!
Divergenţa (div)Divergenţa – div : este un operator matematic care se aplică
întotdeauna unui vector şi are ca efect obţinerea unui scalar.
Exemplu: prin aplicarea operatorului div vectorului S , se obţine
scalarul T:
div S T
S
S
S
T divS x y z
x
y
z
179
180. Continuare Avem nevoie de ceva matematică !!
Transformata StokesTransformata Stokes – această transformată permite trecerea de la
integrala simplă, pe contur, la integrala dublă, pe suprafaţă:
l
E dl
rotE dA
l
S
Unde Sl este o suprafaţă închisă care se sprijină pe conturul închis l.
180
181. Continuare Avem nevoie de ceva matematică !!
Transformata Gauss – OstrogradskiTransformata Gauss – Ostrogradski – permite trecerea de la integrala
dublă, de suprafaţă, la integrala triplă, de volum.
D dA S div D dV
S
V
unde, VS este volumul care se sprijină pe suprafaţa S.
181
182. Continuare Avem nevoie de ceva matematică !!
Circulaţia unui vectorCirculaţia unui vector – se defineşte ca fiind integrala de linie aplicată
vectorului respectiv; are ca efect obţinerea unei mărimi scalare:
Exemplu: circulaţia vectorului pe conturul l se calculează cu expresia:
l
E dl
Circulaţie înseamnă integrală simplă (şi atunci apare obligatoriu şi dl )
182
183. Continuare Avem nevoie de ceva matematică !!
Fluxul unui vector printr-o suprafaţăFluxul unui vector printr-o suprafaţă – se defineşte ca fiind integrala de
suprafaţă aplicată vectorului respectiv; are ca efect obţinerea unei
mărimi scalare:
E
Exemplu: fluxul vectorului
pe suprafaţa S se calculează cu expresia:
E dA
S
Fluxul înseamnă o integrală dublă (şi atunci apare obligatoriu şi dA )
183
184. 1.19. Teorema lui Gauss
Fluxul intensităţii câmpului electrostatic în vid, E , pe o suprafaţăînchisă, , este egal cu raportul dintre cantitatea totală de sarcină
conţinută în interiorul suprafeţei, , şi permitivitatea electrică a
vidului, 0.
E
q
E dA
0
184
185. 1.19.1. Concluzii la Teorema lui Gauss
1.2.
3.
4.
5.
Fluxul vectorului E nu depinde de forma suprafeţei . Din acest
motiv, suprafaţa se alege de o formă cât mai convenabilă pentru a
E dA ;
putea efectua uşor calculul
Fluxul vectorului E nu depinde de modul în care este distribuită
sarcina în interiorul domeniului, ci de cantitatea totală de sarcină q
din interiorul acestuia;
Teorema lui Gauss se aplică numai în vid (prezenţa lui 0);
Teorema lui Gauss este un caz particular al legii fluxului electric (se
va demonstra ulterior);
Teorema lui Gauss se aplică pentru a determina intensitatea
câmpului electrostatic în vid (ca mărime scalară). Ea poate fi aplicată
numai dacă mai există informaţii suplimentare cu privire la simetria
câmpului. Aceste
informaţii permit determinarea direcţiei şi sensului
vectorului E .
185
186. 1.19.2. Consecinţe ale Teoremei lui Gauss
Definiţie:Se numeşte tub de flux totalitatea liniilor de câmp conţinute în
interiorul unui domeniu (suprafaţă care se sprijină pe un mic contur l ).
linie de câmp
dA
E
Sl
tub de flux
E
dA
Sb
dA E
Sb
l
linii de câmp
linie de câmp
Concluzie:
În tubul de flux, fluxul se conservă. 1 2
(Continuitatea fluxului într-un tub de flux).
186
187. 1.20. Teorema potenţialului electrostatic
Se ştie expresia intensităţii câmpului electrostatic în vid:1 l dl r
E
l
3
4 0
r
S dA r
3
S
r
V dV r
3
V
r
n
i 1
qi ri
ri3
Se defineşte potenţialul câmpului electrostatic într-un punct oarecare al
său:
1 l dl
V
l
4 0
r
S dA
S
r
S dV
V
r
n
i 1
qi
ri
Potenţialul V este o mărime scalară (spre deosebire de intensitatea
câmpului E care este o mărime vectorială).
Potenţialul V se măsoară în Volţi [V].
187
188. Continuare Teorema potenţialului electrostatic
Continuare1.
Teorema potenţialului electrostatic
Teorema potenţialului electrostatic scalar – prima formă locală
E grad V
Intensitatea câmpului electrostatic în vid reprezintă gradientul cu
semn schimbat a potenţialului electric.
188
189. Continuare Teorema potenţialului electrostatic
Continuare1.
Teorema potenţialului electrostatic
Teorema potenţialului electrostatic scalar – a doua formă locală
rot E 0
Rotorul intensităţii câmpului electrostatic în vid este nul.
189
190. Continuare Teorema potenţialului electrostatic
Teorema potenţialului electrostaticContinuare
1.
Teorema potenţialului electrostatic scalar (forma globală integrală)
Circulaţia vectorului intensitate câmp electrostatic, pe orice contur
închis l este întotdeauna nulă.
E dl 0
l
Ce-mi spune mie formula aceasta ?
E grad V
Existenţa unui câmp atrage obligatoriu existenţa unei variaţii a
potenţialului.
Mai ţii minte?
gradientul înseamnă variaţia mărimii (dintr-un punct în altul)
împărţită la distanţa dintre puncte.
Aici calculezi gradientul şi schimbi apoi semnul
190
191. Am înţeles bine ?
1.Dacă potenţialul V nu variază înseamnă că nu există
câmp, adică E = 0 ?
Da, dacă ΔV = 0, rezultă grad V = 0, rezultă E = 0.
Nu există câmp.
191
192. Continuare Am înţeles bine ?
Continuare2.
Am înţeles bine ?
Mă pot oare “izola într-un câmp”, adică, chiar dacă el există, să nu îl
simt
Da, şi dispozitivul respectiv se numeşte cuşca lui Faraday.
Cuşca lui Faraday este o încăpere construită numai din metal şi
chiar dacă este plasată într-un câmp electric, în interiorul ei are
câmpul electric nul
192
193. Continuare Am înţeles bine ?
Continuare3.
Am înţeles bine ?
Cum de e posibil ?
Cuşca fiind din metal şi plasată în câmp se va încărca cu
electricitate dar aceasta se va distribui numai superficial şi în
interior nu ai câmp electric.
Dacă e legată la pământ, sarcina se va scurge în pământ.
193
194. Cuşca lui Faraday
A apărut un trăsnet, deci un câmp electricfoarte puternic.
Cuşca, chiar dacă se află în acest câmp
puternic, e izolată în interior şi persoana de
acolo nu păţeşte nimic.
Sarcina electrică apărut în urma descărcării
pe suprafaţa metalică (exterioară) a cuştii
“rămâne acolo, nu intră în interior”.
Dacă cuşca e legată la pământ sarcina se
scurge la pământ, tot fără a se “infiltra în
interior”, unde rămâi protejat.
194
195.
VIDEO (11)195
196.
VIDEO (30)196
197. ” Ce se întâmplă dacă un fulger loveşte un avion în zbor “ ?
Nu se întâmplă nimic.Intră în ecuaţie principiul unei cuştii Faraday.
Practic, “se produc”. 2 găuri mici în fuzelaj acolo unde a „lovit” şi în
coadă (pe unde a „descărcat”). Pilotul e obligat să anunţe că a fost lovit
de fulger în timpul zborului si când avionul e tras la hangar pentru
reparaţii tehnicienii caută semnele respective (şi înlocuiesc bucăţile
respective de fuzelaj).
Cei cărora le e teama să nu fie trăsniţi în maşină, aveţi grijă să staţi cu
geamurile închise când plouă
(Parcă totuşi nu aş dori să verific “experimental” acest adevăr).
197
198. „De ce se întâmplă toate acestea ?”
Pentru că există sarcini electrice.Care creează un câmp electric.
Apar alte sarcini electrice.
Între sarcini se pot exercita forţe (de atracţie sau de respingere)
În câmp sunt tensiuni electrice.
Pot apare curenţi electrice.
Şi multe altele !!
198
199. Vrei să ştii ce e tensiunea de pas ?
În dreptul conductoarelor electrice aeriene de tensiuni mari, în sol deinduc potenţiale.
În punctul aflat chiar sub conductor potenţialul e cel mai mare, apoi el
scade pe măsură ce ne deplasăm mai la stânga sau la dreapta.
Astfel, între 2 puncte de pe sol aflate la o distanţă mică (distanţa de un
pas = 0,8 m) există o tensiune electrică. Dacă gradientul tensiunii în
zona respectivă e mare (grad V =ΔV/ Δx), înseamnă că tensiunea e
mare.
Corpul uman este bun conducător de electricitate având o rezistenţă
cam de 20kΏ. Dacă ai o tensiune între cele 2 picioare, prin tine circulă
un curent. Dacă tensiunea e mare, curentul va fi mare şi te poţi
electrocuta.
Fenomenul este periculos dacă cade un trăsnet în apropiere de tine.
De aceea pe timp de furtună trebuie să te deplasezi cu paşi mici (la paşi
mici tensiunea între cele 2 picioare e mai mică decât la paşi mari)
199
200. Să văd dacă am priceput
Dacă fac paşi mari tensiunea de pas e mare?Da.
200
201. Să văd dacă am priceput
Înseamnă că un cal e mai supus pericolului decât mine?Aici intervine şi rezistenţa. La om e 20.000. Dacă la cal e tot
20.000 (sau mai mică) ai dreptate.
(de fapt, să-ţi spun că
rezistenţa e dată, în special de volumul zonei abdominale; dacă e
mare, rezistenţa e mică).
201
202. Să văd dacă am priceput
Deci e clar, un cal are o rezistenţa mai mică, deci e supus pericoluluimai mult
Da, e perfect acum.
De aceea, în zonele electrificate se iau măsuri speciale pentru ca
animalele mari să nu fie electrocutate accidental.
202
203. Ce pune în evidenţă teorema potenţialului
1.În câmpul electrostatic nu se poate manifesta fenomenul de
inducţie electromagnetică.
2.
Liniile de câmp ale lui sunt irotaţionale (ele nu se închid pe ele
însele; încep de pe sarcina pozitivă şi se sfârşesc pe sarcina
negativă; dacă sarcina negativă lipseşte, ele se sfârşesc la infinit)
Sensul liniilor de câmp
E
“ies” din sarcina pozitivă
E
“intră“ în sarcina negativă
203
204. VIDEO 80
204205. Continuare Ce pune în evidenţă teorema potenţialului
Continuare3.
Ce pune în evidenţă teorema potenţialului
Sarcinile (+) circulă în sensul
liniilor de câmp. Sarcinile (-)
circulă în sens invers.
E
F
E logic, nu ?
2 sarcini de acelaşi semn se resping;
Pentru că la sarcina pozitivă liniile de câmp ies din sarcină, e clar că q+ se
deplasează în sensul liniilor de câmp.
205
206. Consecinţe ale teoremei potenţialului electrostatic
1.Determinarea tensiunii dintre 2 puncte, a şi b : Uab
Teoremă:
Circulaţia vectorului între 2 puncte reprezintă tensiunea electrică
dintre cele două puncte.
a
b
a
E dl U ab
E
dl
l b
E vectorul intensitate câmp electric
(are direcţie radială şi sens, “iese”
din sarcina pozitivă
dl element infinitezimal al curbei l
(traseul de integrare)
l traseul de integrare de la a la b
206
207. Continuare Consecinţe ale teoremei potenţialului electrostatic
2.Independenţa calculului tensiunii de drumul de integrare
Teoremă:
Calculul tensiunii între punctele a şi b nu depinde de traiectoria
aleasă pentru a parcurge drumul din a în b, ci depinde numai de
poziţia punctelor a şi b.
b
E dl
a ( m)
b
E dl
a E
a(n)
m traseul m
n l b
cel mai avantajos traseu de integrare
traseul n
În cazul desenului, cel mai avantajos traseu de integrare
(corespunzător căruia calculul matematic este cel mai simplu) este
cel care uneşte în linie dreaptă (coliniar cu ) punctele a şi b. Pentru
că rezultatul este acelaşi, indiferent pe ce traseu merg din punctul a
în punctul b, acesta este traseul recomandat pentru a efectua
integrala
b
U ab
a (l )
E dl
207
208. Continuare Consecinţe ale teoremei potenţialului electrostatic
Continuare1.
Consecinţe ale teoremei potenţialului electrostatic
Determinarea potenţialului unui punct
Tensiunea dintre 2 puncte reprezintă diferenţa de potenţial între cele
2 puncte:
a
E
l
b
de obicei punctul b este situat la
distanţă foarte mare - la infini faţă de punctul a.
El trebuie să aibă potenţialul
Vb= 0
U ab Va Vb
Întotdeauna, potenţialul unui punct a nu poate fi determinat decât în
funcţie de potenţialul (numit de referinţă), unui alt punct b, (numit
punct de referinţă).
Va Vb ( 0 )
b (0)
a
E dl
unde: b(0) este un punct numit punct de referinţă, astfel ales încât
potenţialul său, Vb (0) 0
.
208
209. Continuare Consecinţe ale teoremei potenţialului electrostatic
U abLba
q
Continuare
4.
Consecinţe ale teoremei potenţialului electrostatic
Interpretarea energetică a noţiunii de tensiune electrică
Teoremă:
Tensiunea electrică Uab dintre 2 puncte a şi b este numeric egală cu
lucrul mecanic L efectuat de forţa exterioară pentru a deplasa din
punctul b în a sarcina electrică unitară (q = 1C).
Forţa electrostatică tinde să
deplaseze sarcina q+ spre
dreapta (este o forţă de
Lba
respingere pentru că sarcinile
U
ab
b Fe
aE
q
sarcinile şi q+ au acelaşi semn).
Fext.q
Forţa exterioară este egală şi de
semn contrar cu . Dacă notăm
cu d distanţa dintre a şi b
obţinem:
Lba F ext
L
d Fext d Fe d qE d qU ab U ab ba
q
209
210. Cât de mare este potenţialul pentru un câmp creat de un generator Van de Graaff ?
Îmi amintesc:Expresia potenţialului V creat de o sarcină punctiformă q la o distanţă r
V
1 q
q
; 0 8,856 10 12 V 9 109
4 0 r
r
R
Dacă am o sferă metalică de rază R încărcată cu sarcina q,
sarcina se distribuie uniform pe toată suprafaţa sferei.
Pentru puncte exterioare sferei câmpul se comportă ca şi
cum toată sarcina q se află concentrată în centrul sferei.
q
Raza sferei generatorului Van de Graaff este aproximativ 0,3m.
Sarcina q care se acumulează la acest generator este q = 10 µC (micro
r1 0,3m V1 300 kV .
Coulombi) pentru
(Pe suprafaţa sferei
generatorului)
pentru
r2 0,6m
V2 150 kV
pentru
r3 1,2m
V3 75 kV
210
211. Experiment 1
Avem un câmp creat de un generator Van de GraaffPun un tub de neon radial în câmp (în lungul liniilor de câmp).
Pentru că pe distanţe mici potenţialul câmpului scade foarte mult,
mă aştept ca la capetele tubului de neon tensiunea să fie foarte mare.
Dacă lungimea l a tubului de neon este mare, tensiunea de la capete
este mare;
l 0,6m r3 r2 V V2 V3 150 75 75kV
ex:
V2
V3
R
Tub de neon dispus pe
o direcţie radială
Tubul luminează.
211
212. Experiment 2
Stau cu picioarele pe pământ. Voi avea potenţialul V = 0.Dacă ating capătul din dreapta a tubului fac ca potenţialul acestui
punct să fie zero V3 0 .
Tensiunea dintre capetele tubului creşte şi mai mult devenind:
V V2 0 150 0 150 kV
Tubul luminează mai puternic.
212
213. Experiment 3
Cum de nu mă electrocutez când pun mâna pe capătul tubului dacă potenţialuleste atât de mare?
V2
V3 = 0
R
Tub de neon dispus pe
o direcţie radială
leg capătul din dreapta la pământ
Potenţialul va deveni V =0
Între degetul meu şi pământ tensiunea va fi mare.
Chiar dacă tensiunea este mare (de ordinul kV) curentul este mic.
Observ că acest curent este mic pentru că şi luminarea tubului, chiar
dacă are tensiune de aprindere, nu este prea puternică.
Generatorul Van de Graaff creează sarcini puţine (ai văzut ca am luat în
calcul o sarcină q = 10 µC
Prin legătura la pământ va circula un curent , i
q
dar, pentru că
t
sarcina este foarte mică şi acest curent este foarte mic şi nu mă
electrocutez.
213
214. Experiment 4
Pun un tub de neon perpendicular în câmpCapetele tubului sunt aproximativ la aceeaşi distanţă d faţă de sfera
generatorului. Prin urmare, la capetele sale potenţialul este
aproximativ egal şi tensiunea va fi nulă:
U V V 0
d
V
Tub de neon dispus pe o
direcţie perpendiculară
pe direcţia câmpului
R
d
V
Tubul nu va lumina.
214
215.
VIDEO ( 12 )215
216. Ai obosit şi doreşti ceva să te deconectezi ?
Ştii de ce ?Forţa se măsoară în Newtoni (N) ?
Potenţialul (sau tensiunea electrică) se măsoară în Volţi (V) ?
Sarcina electrică se măsoară în Coulombi (C) ?
Capacitatea electrică se măsoară în farazi (F) ?
Lucru mecanic în Jouli (J) ?
Multe din unităţile de măsură ale mărimilor fizice au fost date în
cinstea unor mari savanţi cu contribuţii deosebite la dezvoltarea
ştiinţei.
216
217.
Isaac Newton(1643-1728)
părintele Mecanicii (Om de ştiinţă şi
filozof englez). Cartea sa „Philosophiæ
Naturalis
Principia
Mathematica”,
publicată în 1687, este considerată cartea
cu cea mai puternică influenţă în istoria
ştiinţei.
A descoperit cele mai importante legi ale
Mecanicii (legea atracţiei universale,
legea gravitaţiei, principiile mişcării).
În onoarea sa, unitatea de măsură pentru
forţa a fost denumită Newton (N).
1N este forţa care aplicată unui corp cu
masa de 1 kg îi produce acesteia o
acceleraţie de 1m/s2
F ma
217
218.
Alessandro Volta(1745-1827)
descoperitorul bateriei.
Profesor la Universitatea din Como,
Italia.
În 1800 a inventat şi construit prima
baterie electrică, prima sursă de tensiune
continuă.
În cinstea sa, unitatea de măsură în
Sistemul Internaţional a tensiunii a fost
denumit Volt-ul.
1 Volt (1 V) este tensiunea electrică care
aplicată unui rezistor de 1 Ohm (1 Ώ) dă
naştere unui curent electric
intensitatea de 1 Amper (1 A).
având
U RI
218
219.
Augustin de Coulomb(1736-1806)
Om de ştiinţă francez. Descoperirea cea
mai importantă o reprezintă Legea lui
Coulomb, care defineşte forţa de
interacţiune (atracţie sau respingere)
dintre 2 corpuri încărcate electric.
În onoarea sa unitatea de măsură a
sarcinii electrice este Coulombul (C)
1 Coulomb (1C) este sarcina electrică cu
care sunt încărcate 2 sarcini electrice,
plasate în vid la distanţă de 1 metru (1
m), între care se exercită o forţă de
1 Newton (1N).
qq r
F 1
4 0 r 3
219
220.
Michael Faraday(1791-1867)
Om de ştiinţă englez care a studiat
câmpul magnetic creat la trecerea
curentului electric prin conductoare şi a
formulat
principalele
legi
ale
electromagnetismului.
Numele său a fost folosit pentru
denumirea în Sistemul Internaţional de
unităţi de măsură a capacităţii electrice.
Un condensator are o capacitate electrică
de 1 Farad (1 F) dacă el se încarcă cu o
sarcină electrică de 1 Coulomb (1 C)
atunci când i se aplică o tensiune de 1
Volt (1 V ).
Q CU
220
221.
James Prescott Joule(1818-1889)
Fizician englez care a descoperit
echivalentul mecanic al căldurii (legătura
dintre cantitatea de căldură şi lucru
mecanic).
Numele său a fost folosit în denumirea
unităţii de măsură a cantităţii de căldură, a
lucrului mecanic, al energiei.
La trecerea unui curent electric de 1
Amper (1 A) printr-o rezistenţă de 1 Ohm
(1 Ώ) timp de 1 secundă (1 s) se dezvoltă o
energie (care se degajă sub formă de
căldură) de 1 Joule (1 J)
W RI 2 t
221
222. 1.21. Exerciţii
Întrebarea 1Dacă ai două sarcini, una negativă şi una pozitivă plasate una sub
alta, cea pozitivă fiind „sus” şi cea negativă „jos”.
Cum este orientat câmpul creat de cele 2 sarcini „între ele”?
a) În jos
b) În sus
c) La stânga
d) La dreapta
222
223. Exerciţii
Răspuns întrebarea 1Câmpul iese din sarcina pozitivă şi intră în sarcina negativă.
Deci, câmpul rezultant, între cele 2 sarcini este în jos
Răspuns corect varianta a)
223
224. Exerciţii
Întrebarea 2Cum se va deplasa sarcina pozitivă din figură ?
a)
b)
c)
Spre stânga
Spre dreapta
Nu se deplasează
E
224
225. Exerciţii
Răspuns întrebarea 2Sarcina pozitivă se deplasează în sensul liniilor de câmp.
Răspuns corect: varianta b)
E
F
225
226. Exerciţii
Întrebarea 3a)
b)
c)
d)
Avem o sferă confecţionată dintr-un material conductor neîncărcată
electric. O atingi de o sferă încărcată pozitiv. Firesc, de pe sfera
încărcată se transferă sarcini pe sfera iniţială.
Unde se distribuie acestea ?
Rămân în punctul de atingere.
Se distribuie pe o mică suprafaţă în jurul
Sferă încărcată
pozitiv (+)
punctului de atingere.
Se distribuie uniform pe toată suprafaţa
Sferă confecţionată dintr-un
sferei.
material conductor
Se distribuie în tot volumul sferei dacă e
plină.
226
227. Exerciţii
Răspuns întrebarea 3Corpurile conductoare se încarcă întotdeauna cu sarcină
distribuită superficial
Toată suprafaţa corpului trebuie să aibă acelaşi potenţial. Deci
sarcina nu poate să se „izoleze” pe o suprafaţă mică.
Răspuns corect: varianta c)
227
228. Exerciţii
Întrebarea 4Avem o sferă 1 confecţionată dintr-un material conductor neîncărcată
electric. O atingi de o sferă 2 încărcată pozitiv. Firesc, de pe sfera 2
încărcată se transferă sarcini pe sfera 1.
Cu ce sarcină se încarcă sfera 1 ?
1
2
a)
b)
c)
Pozitivă
Negativă
Nu poţi preciza, depinde de mărimea sferelor
?
228
229. Exerciţii
Răspuns întrebarea 4Prin atingere se transferă sarcină (în cazul nostru pozitivă) de pe
sfera 2 pe sfera 1.
Răspuns corect : varianta a)
229
230. Exerciţii
Întrebarea 5Avem un corp conductor (C.c.)
neîncărcat electric. Îl apropii de un corp
încărcat negativ (de ex. un generator
Van de Graaff GVG)
Ce se întâmplă ?
a) Nimic pentru că nu ai atins corpul
(C.c.) de generatorul GVG pentru ca
sarcinile să se poată transfera:
b)
c)
d)
corp conductor
neutru (Cc.)
(G.V.G.)
corpul (C.c.) se încarcă pozitiv;
corpul (C.c.) se încarcă negativ;
corpul (C.c.) rămâne neutru din punct de vedere electric, dar
sarcina se distribuie diferit.
230
231. Exerciţii
Răspuns întrebarea 5Un corp conductor 1 se poate încărca cu
sarcină adevărată:
Prin atingere de un alt corp conductor
corp conductor
(C.c.). Şi atunci se încarcă cu sarcină de
neutru (C.c.)
acelaşi fel.
Prin influenţă electrostatică, dacă
Generator Van de Graaff
corpurile sunt suficient de apropiate.
(G.V.G.)
Astfel,
corpul (C.c.) rămâne neutru din punct de vedere electric, dar
sarcina de pe corpul (C.c.) se distribuie diferit:
mai aproape generatorul GVG, pe corpul (C.c.) este un surplus
de sarcini pozitivă (+),
mai departe, un surplus de sarcini negative (-).
Răspuns corect: varianta d )
231
232. Exerciţii
Întrebarea 6Avem o sferă 1 confecţionată dintr-un material conductor neîncărcată
electric. O atingi de o sferă 2 încărcată pozitiv. Firesc, de pe sfera 2
încărcată se transferă sarcini pe sfera 1.
1
Cât de multă sarcină se transferă de pe o sferă pe alta ?
2
a) Se transferă toată sarcina q
b) Se transferă jumătate din sarcina q
c) Nu poţi preciza
232
233. Exerciţii
Răspuns întrebarea 6Câtă sarcină se transferă, depinde de capacitatea electrică fiecărei sfere.
Nu uita ! Capacitatea electrică a unui corp conductor este proprietatea
de a înmagazina pe el sarcini electrice.
În cazul unei sfere, capacitatea depinde de raza sferei şi de
permitivitate. După ce s-a realizat transferul de sarcină trebuie însă să
se respecte legea conservării sarcinilor (nimic nu se pierde, nimic nu se
câştigă, totul se transformă). qiniţial qfinal adică q2 q1 q2
Răspuns corect : varianta c)
233
234. Exerciţii
Întrebarea 7Dacă „pui” o sarcină într-un câmp electric ce se întâmplă?
a) Nimic pentru că un câmp electric nu are nici o acţiune asupra
unei sarcini electrice.
b) Asupra ei acţionează o forţă
c) Nimic pentru că sarcina „stă” când ai introdus-o şi nu se
deplasează.
234
235. Exerciţii
Răspuns întrebarea 7Asupra ei se exercită o forţă a cărei expresie este
F qE ,
unde: F - este forţa
q - este sarcina
E - intensitatea câmpului
Răspuns corect: varianta b)
235
236. Exerciţii
Întrebarea 8Ai o sarcină pozitivă q 1 mC având o masă m 1g care este plasată
în vid, în câmpul gravitaţional terestru şi într-un câmp electric orientat
„în sus” având E 10 V / m .
F=q E
Ce se întâmplă cu sarcina ?
E
G=mg
236
237. Exerciţii
Răspuns întrebarea 81.
Dacă sarcina are o masă m atunci ea va fi atrasă de câmpul
gravitaţional cu o forţă G (greutatea)
F m g 10 3 10 10 2 [ N ]
Ca sens, forţa G este îndreptată în jos.
Ai observat, desigur, că:
pe m l-am introdus în calculul numeric în Sistemul internaţional,
adică kg; 1g =10-3 kg.
am considerat g, acceleraţia gravitaţională, g 10 ca fiind (în
calculele exacte g = 9,8).
237
238. Exerciţii
Continuare Răspuns întrebarea 8Dacă sarcina este pozitivă q+ şi câmpul electric este îndreptat în sus,
asupra sarcinii se va exercita o forţă
F q E 10 3 10 10 2 [N ]
Ca sens, forţa F îndreptată în sus.
Ai observat, desigur, că:
pe q l-am introdus în calculul numeric în Sistemul internaţional,
adică: 1 m C = 10-3 C.
Cele 2 forţe sunt egale şi de sensuri contrare (una acţionează în jos şi
cealaltă în sus) şi atunci forţa rezultantă este nulă.
Răspuns corect: Corpul pluteşte în vid.
238
239. Experimentul lui Milikan. „Picătura de ulei în câmp electrostatic”
1.O sarcină pozitivă q + se deplasează în sensul intensităţii câmpului E.
F
239
240. Continuare Experimentul lui Milikan. „Picătura de ulei în câmp electrostatic”
2.Sarcina negativă q- în sens invers lui E. Dacă discutăm de sarcina
negativă, în cazul nostru ea va fi împinsă în sus.
F
240
241. Continuare Experimentul lui Milikan. „Picătura de ulei în câmp electrostatic”
3.4.
Greutatea proprie G a sarcinii e întotdeauna în
jos.
Dacă valorile numerice sunt adecvate s-ar
putea ca F = G să se echilibreze şi particula să
plutească în câmp.
F
241
242. Cum funcţionează un aparat de fotocopiere
În funcţionare se disting 4 etape:1.
Încărcarea: Suprafaţa unui cilindru este încărcată electrostatic
cu sarcini negative de la un conductor aflat la înaltă tensiune (15
kV). Cilindrul are un înveliş dintr-un material fotoconductor devine bun conducător de electricitate când este iluminat - pe
care se depun sarcinile negative.
fotocopiator
15 kV
cilindru
242
243. Continuare Cum funcţionează un aparat de fotocopiere
Continuare2.
Cum funcţionează un aparat de fotocopiere
Expunerea. O lampă puternică luminează documentul original şi
suprafeţele albe ale originalului reflectă lumina pe cilindrul
fotoconductor. Porţiunile din suprafaţa cilindrului expuse la lumină
(cele care corespund suprafeţei albe nescrise - ale originalului) devin
conductoare şi descarcă sarcina depusă iniţial pe ele. Porţiunile din
suprafaţa cilindrului neexpuse la lumină (cele care corespund
suprafeţei scrise ale originalului) îşi păstrează sarcina depusă iniţial
pe ele.
Rezultatul: o imagine de sarcini negative pe suprafaţa cilindrului.
lumină
243
244. Continuare Cum funcţionează un aparat de fotocopiere
Continuare3.
Cum funcţionează un aparat de fotocopiere
Developarea: Tonerul este încărcat pozitiv. Când este aplicat pe
cilindru el este atras de porţiunile cu sarcină negativă de pe cilindru,
adică de porţiunile scrise ale originalului. Aceste sarcinile pozitive
rămân „lipite ” pe cilindru.
244
245. Continuare Cum funcţionează un aparat de fotocopiere
Transferul: Sarcinile pozitive de pe cilindru sunt transferate hârtiei,încărcate cu o mică sarcină negativă. Tonerul depus pe hârtie este fixat
de căldură şi de rolele presoare care apasă pe hârtie.
S-a format în felul acesta imaginea originalului pe hârtie.
hârtie
245








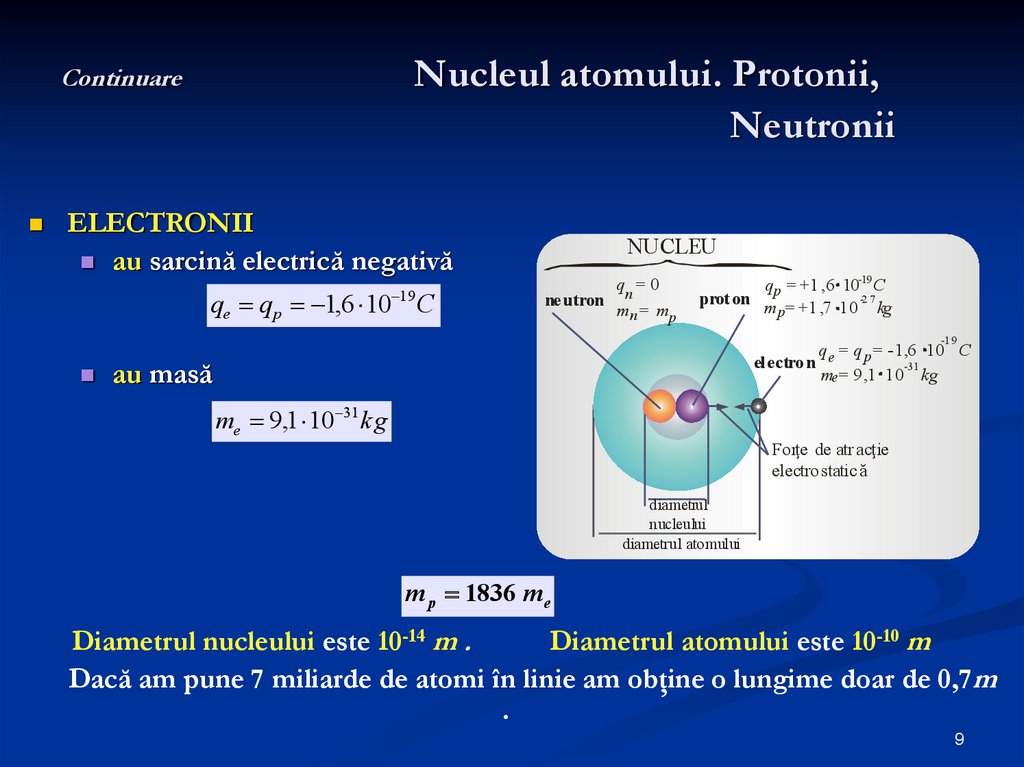


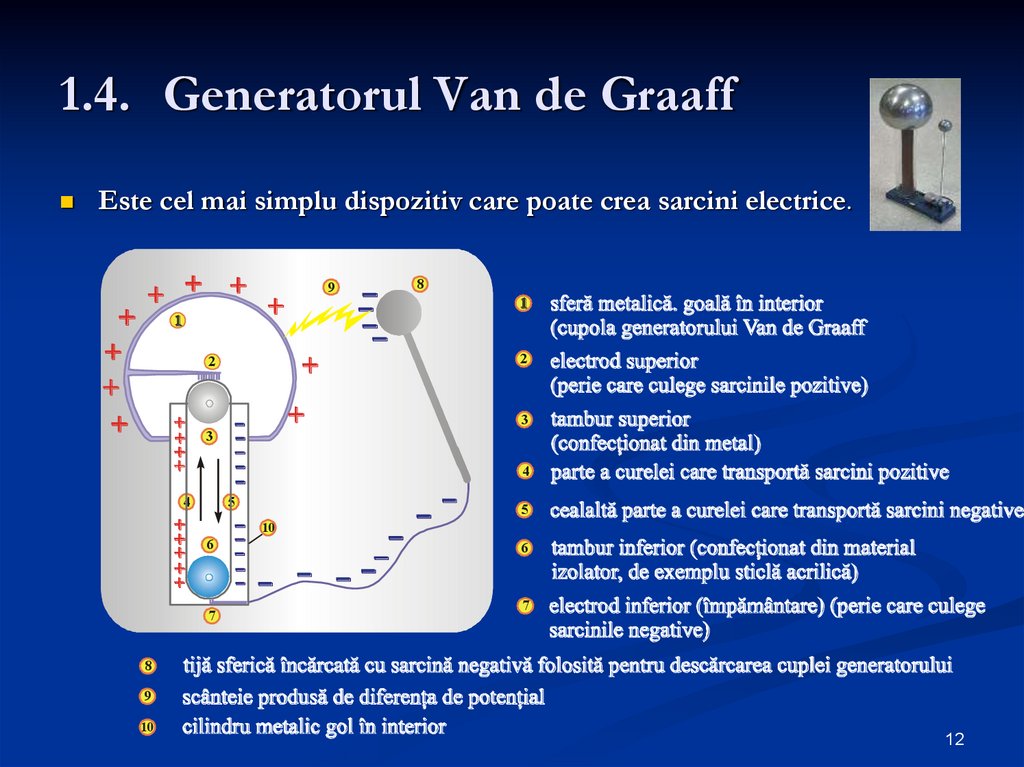




















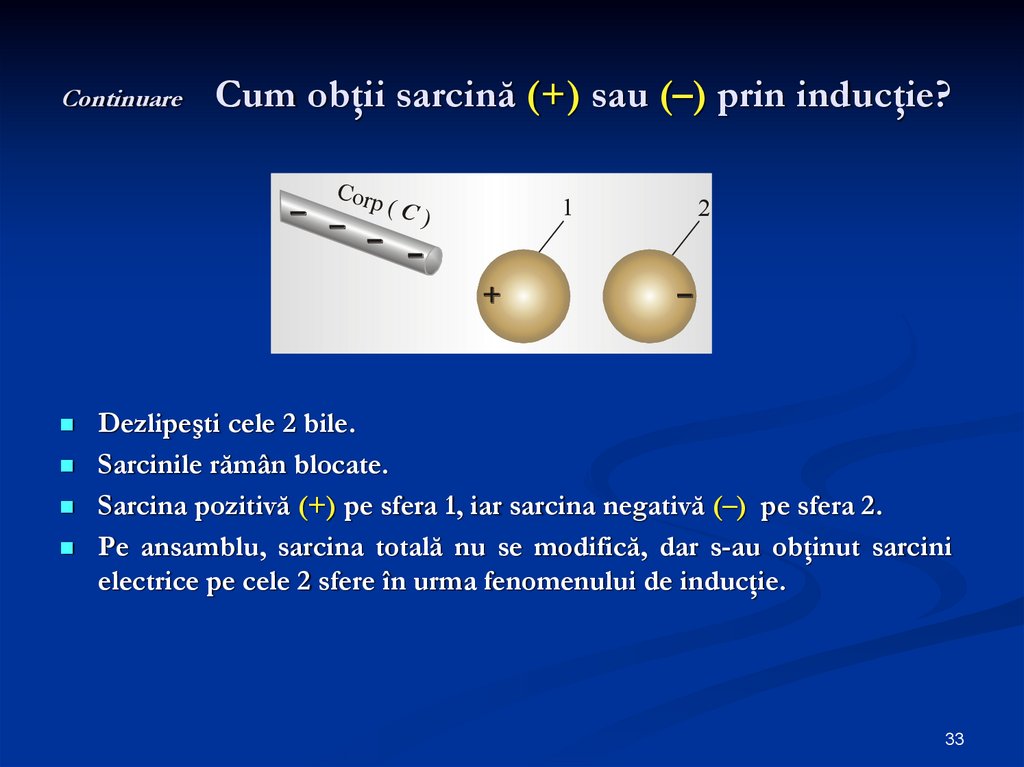
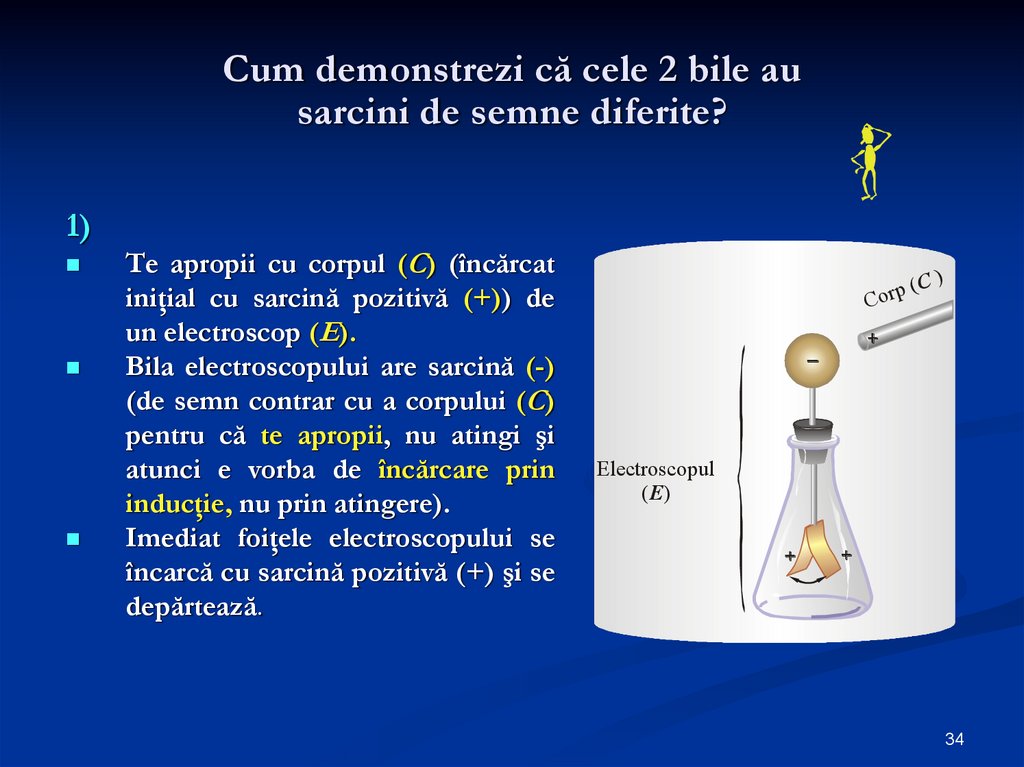









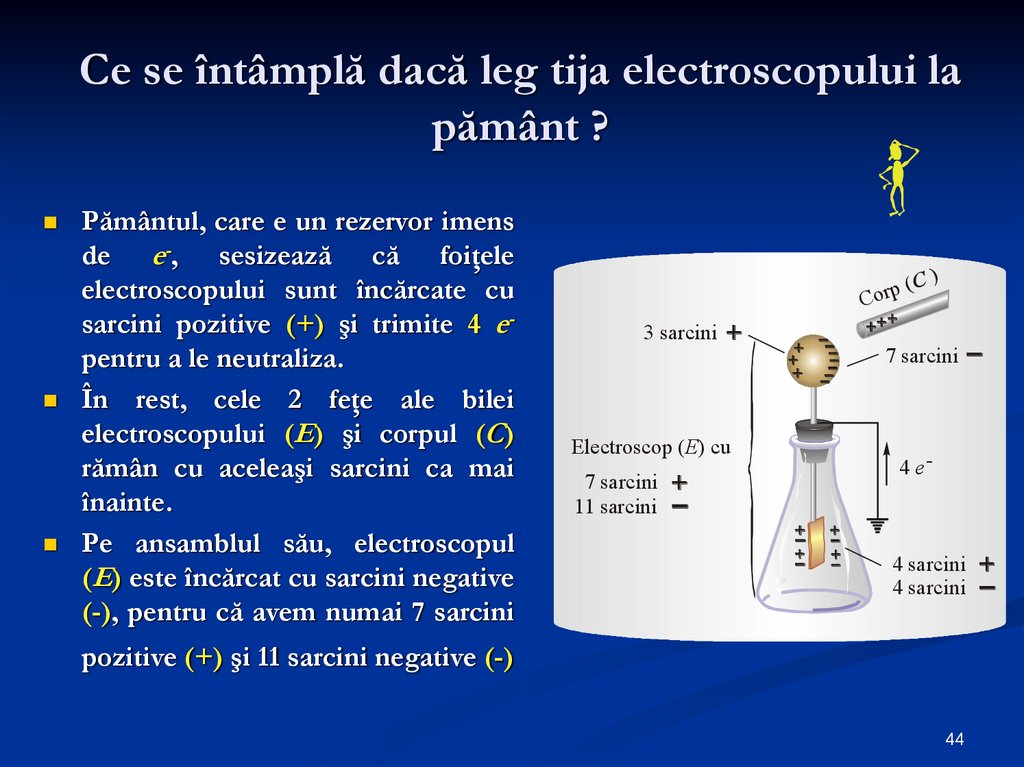















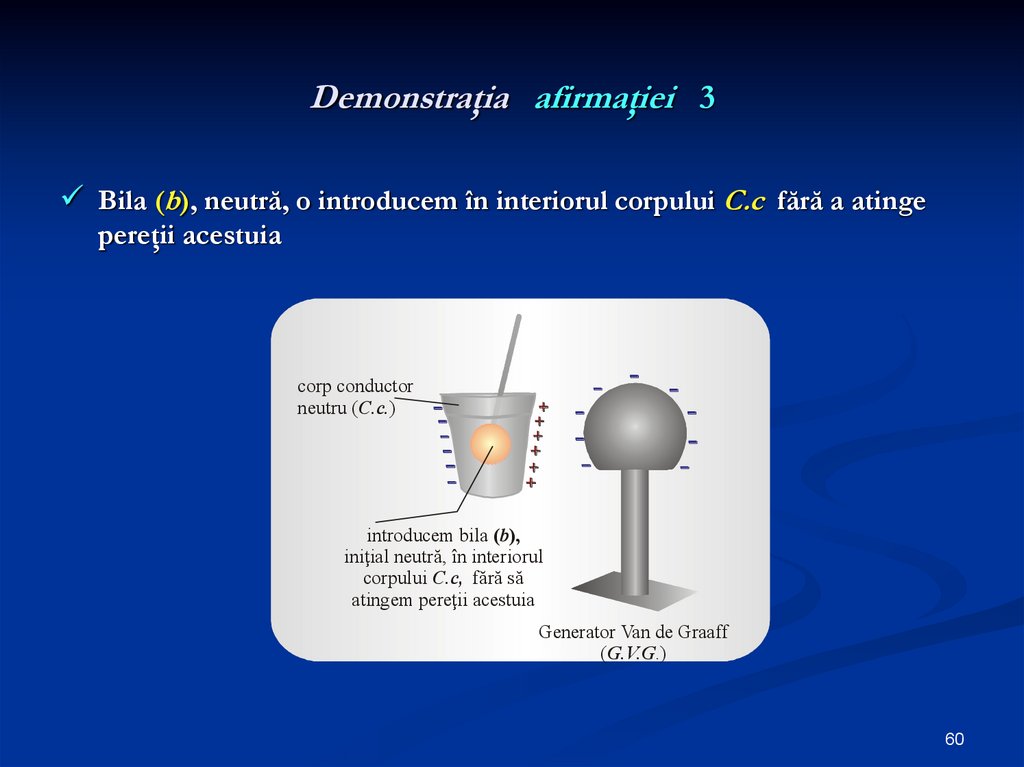
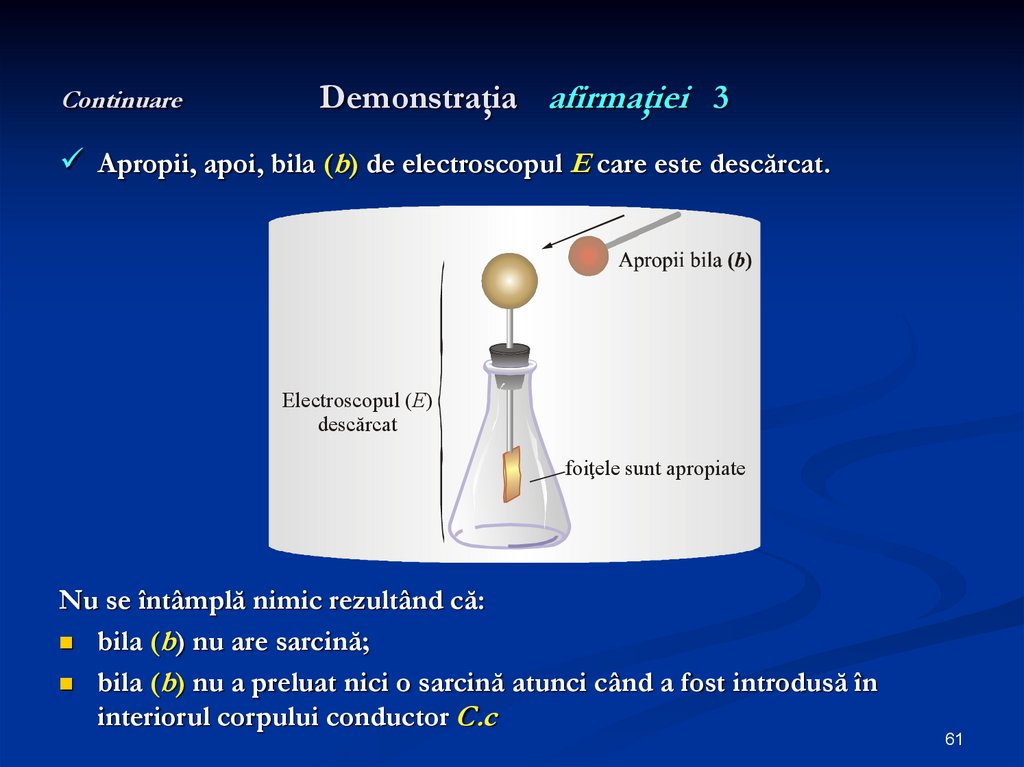

















































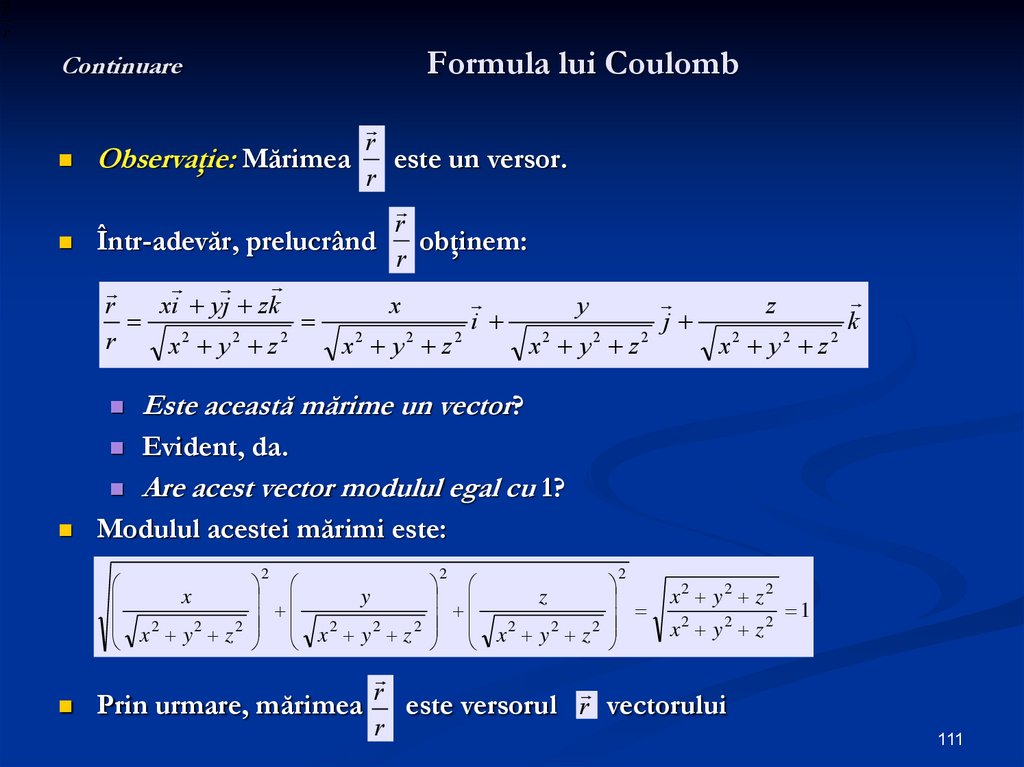












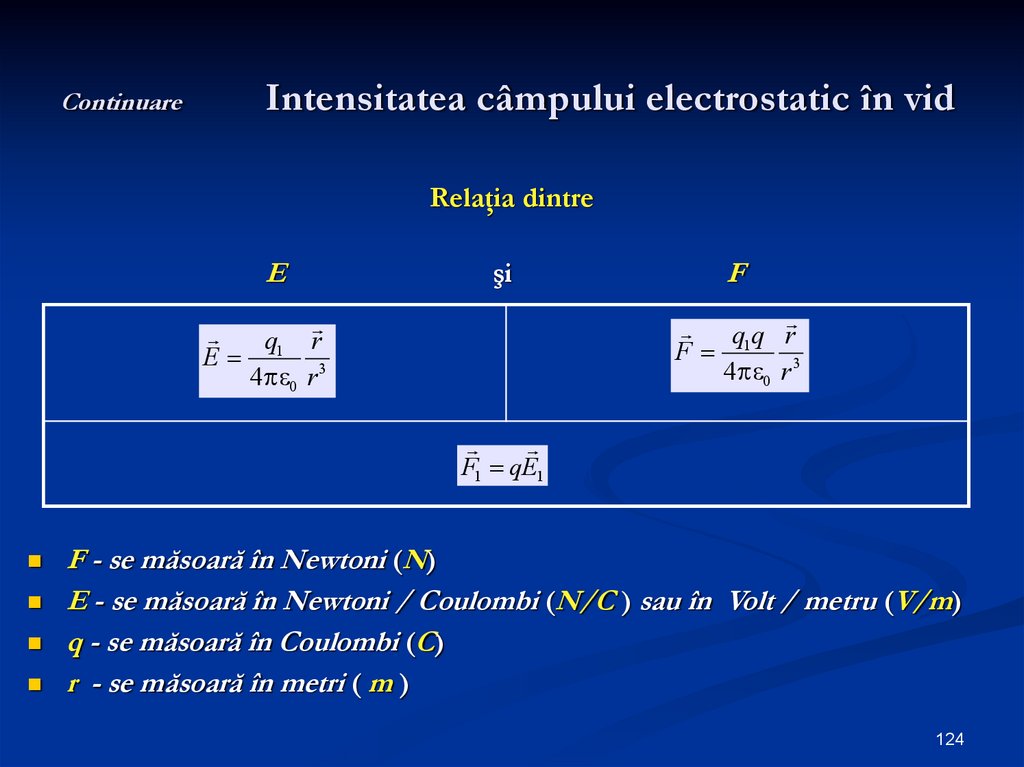


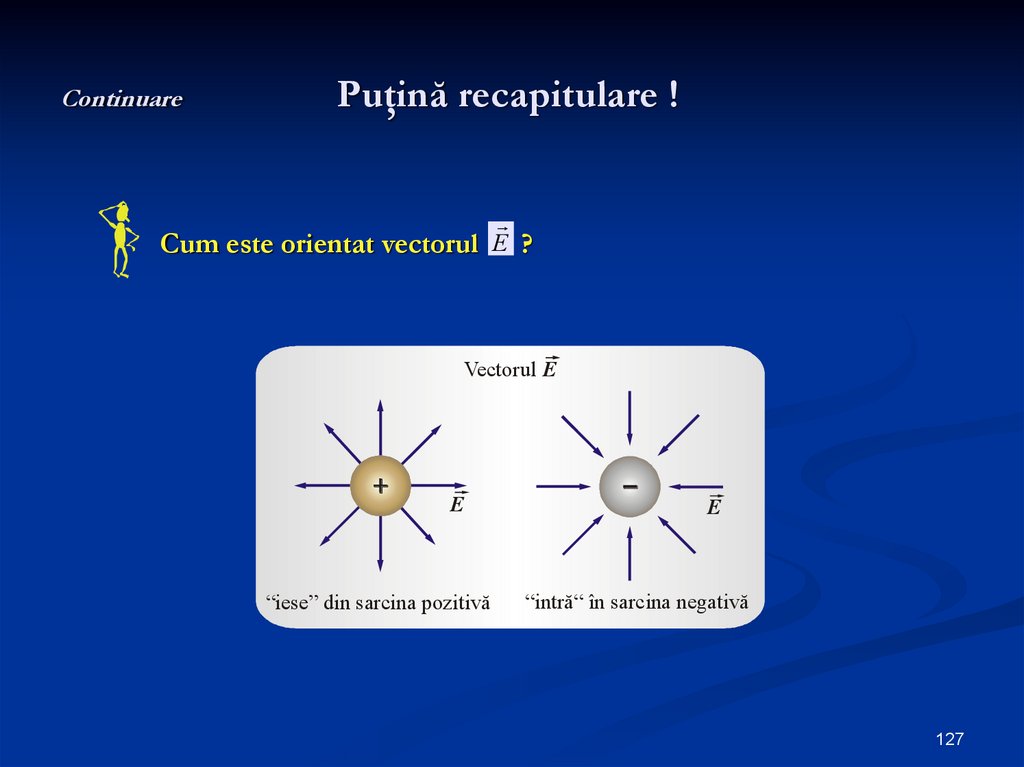


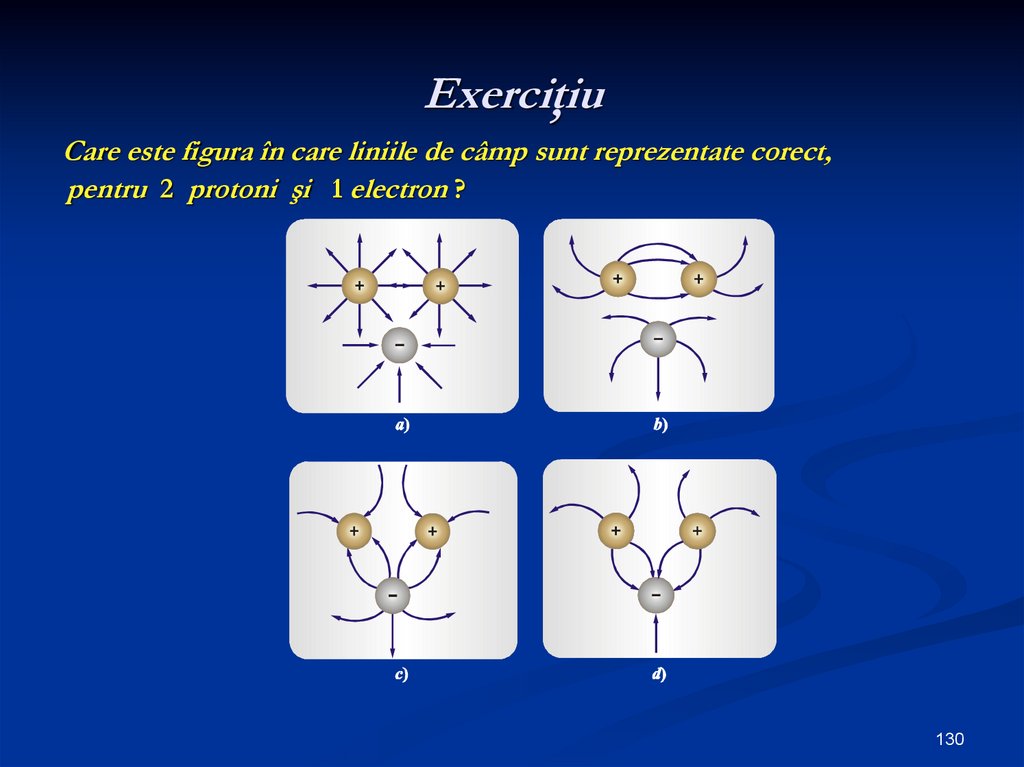


























































































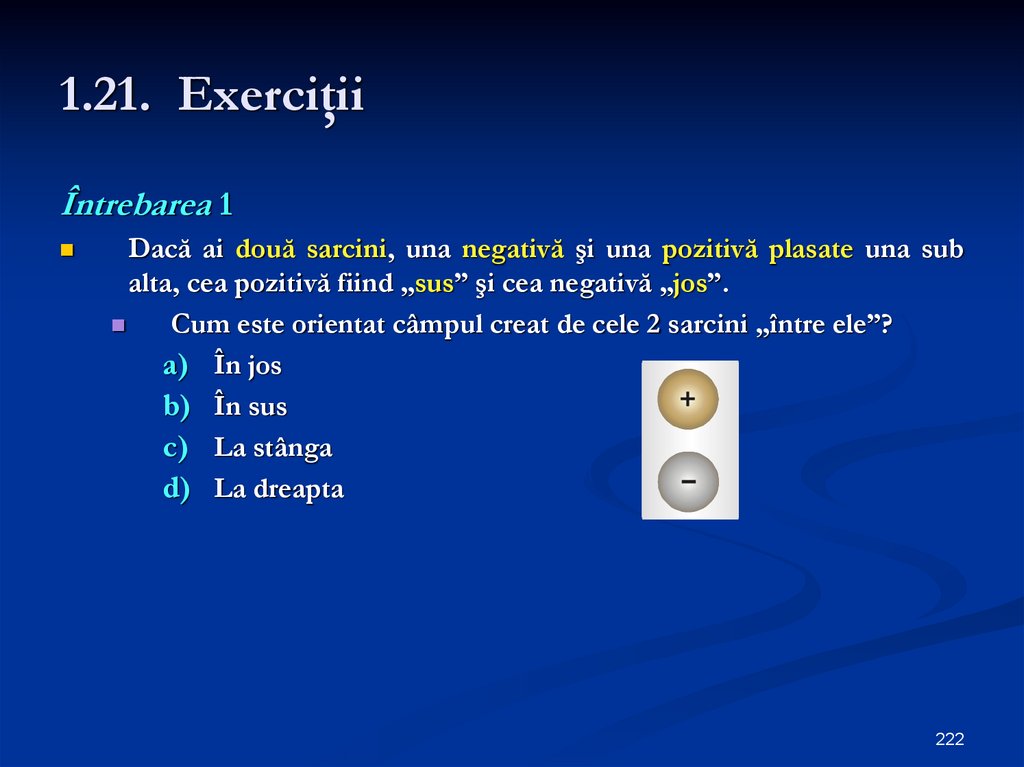


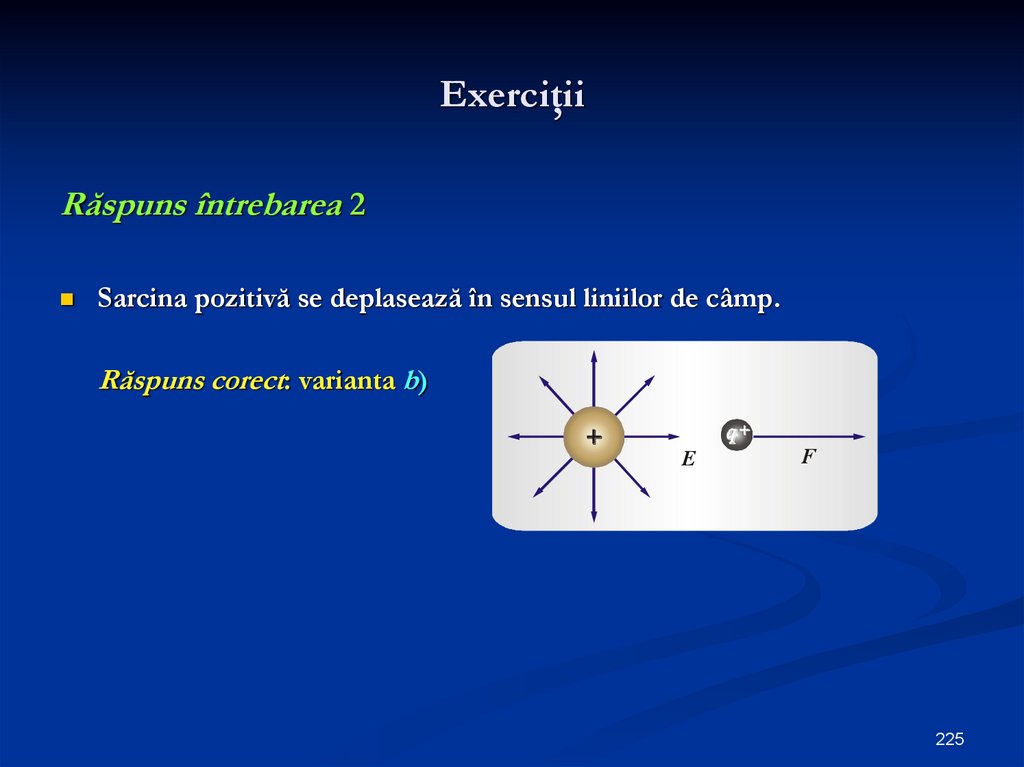




















 physics
physics