Моделирование химико-технологических процессов. Общие понятия

1.

Кафедра технологии керамики и
наноматериалов
Моделирование химико-
технологических процессов
Общие понятия

2.

МОДЕЛИРОВАНИЕ в химической технологии – метод исследования
химико-технологических процессов или систем путем построения и
изучения их моделей, которые отличаются от объектов моделирования
масштабами или физической природой происходящих в них явлений,
но достаточно точно (адекватно) отображающих представляющие
интерес свойства этих объектов.
Моделирование (М) в широком смысле используют для решения
различных задач, в том числе:
1) исследование новых процессов;
2) проектирование производств;
3) оптимизация отдельных аппаратов и технологических схем;
4) выявление резервов мощности и отыскание наиболее эффективных
путей модернизации действующих производств;
5) оптимальное планирование производств;
6) разработка автоматизированных систем управления
проектируемыми производствами;
7) построение автоматизированных систем научных исследований.
2

3.

Для конкретного предприятия или группы родственных или связанных
в цепочку предприятий моделирование позволяет:
создавать модели и рассчитывать процессы для оптимизации
режимов;
регулировать работу установок в целях увеличения выхода
продуктов;
выявлять узкие места и находить резервы увеличения
производительности установок и агрегатов;
оптимизировать работу по критериям прибыльности или
увеличения выхода;
прогнозировать режимы и рассчитывать показатели качества и
свойства продуктов;
выполнять расчетные исследования, создавать экспертные
системы в помощь оператору, динамические тренажеры
операторов.
3

4.

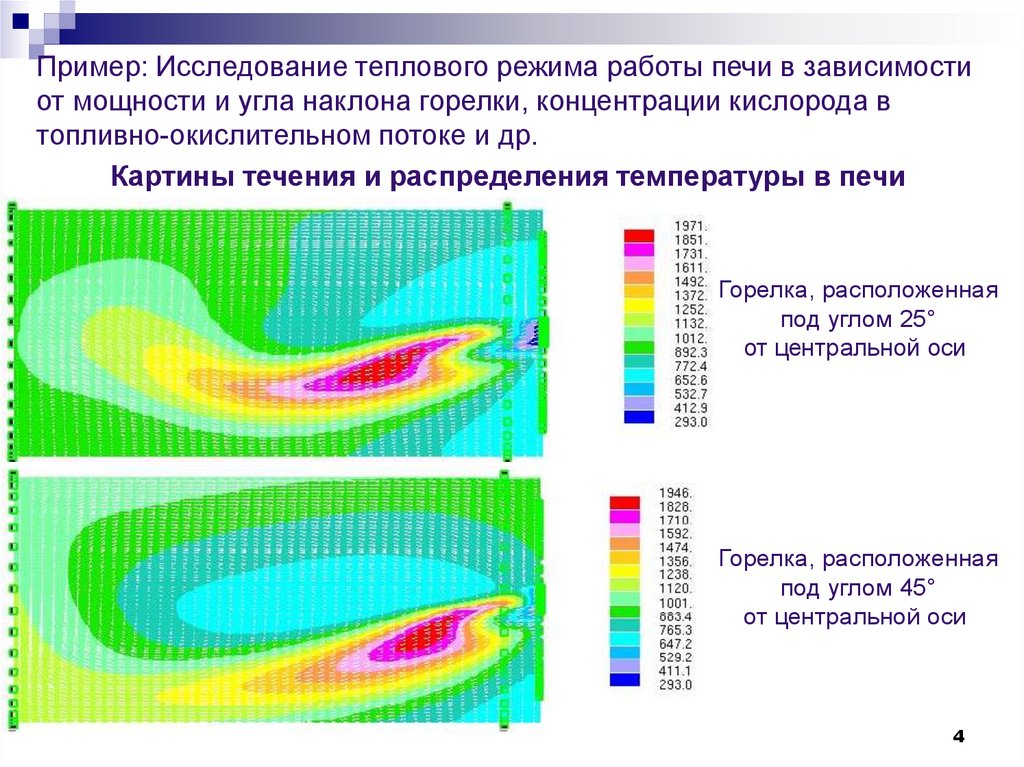
Пример: Исследование теплового режима работы печи в зависимости
от мощности и угла наклона горелки, концентрации кислорода в
топливно-окислительном потоке и др.
Картины течения и распределения температуры в печи
Горелка, расположенная
под углом 25°
от центральной оси
Горелка, расположенная
под углом 45°
от центральной оси
4

5.

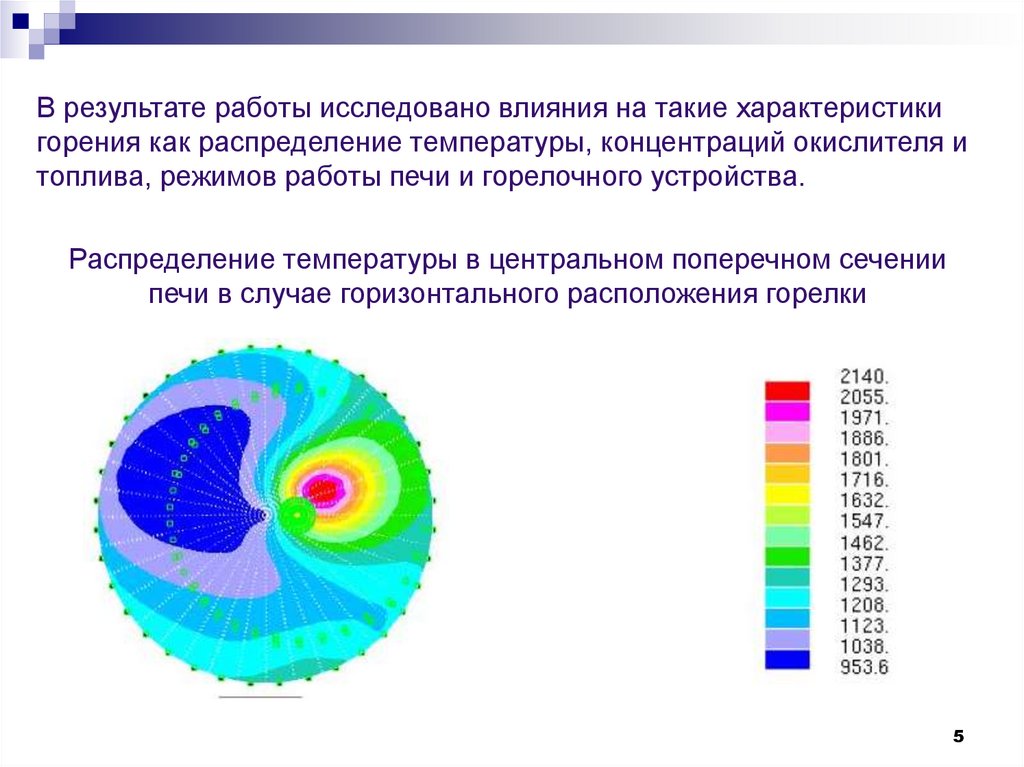
В результате работы исследовано влияния на такие характеристики
горения как распределение температуры, концентраций окислителя и
топлива, режимов работы печи и горелочного устройства.
Распределение температуры в центральном поперечном сечении
печи в случае горизонтального расположения горелки
5

6.

Распределение CO в случае горизонтального расположения горелки
6

7.

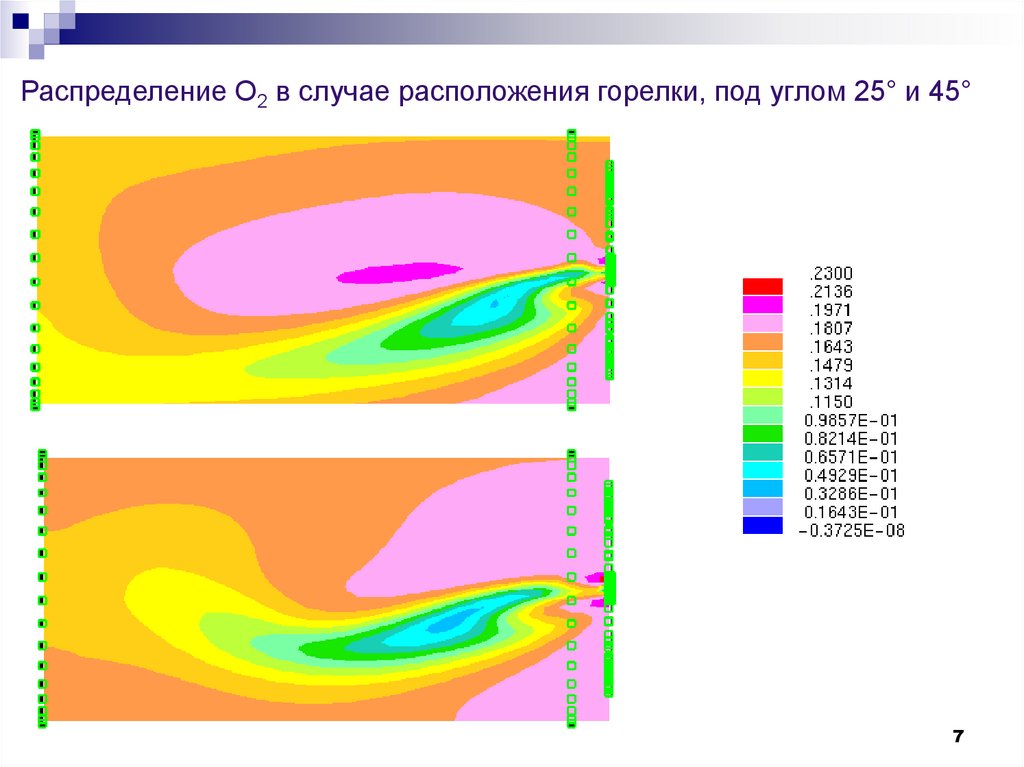
Распределение O2 в случае расположения горелки, под углом 25° и 45°
7

8.

В результате применения моделей могут быть достигнуты
принципиально важные результаты:
уменьшение колебаний основных технологических параметров на
50% или более;
увеличение выхода ценных продуктов и производительности за
счет работы, приближающейся к абсолютному оптимуму;
постоянная индикация параметров качества, не измеряемых
напрямую;
автоматизация быстрых переходов с режима на режим;
увеличение надежности управления установкой;
оптимизация настройки контуров АСУТП и регуляторов.
8

9.

9

10.

Моделирование основано на свойстве подобия разных объектов,
которое может быть физическим и математическим.
Процессы в физически подобных объектах имеют физическую
природу.
В математически подобных объектах процессы описываются
одинаковыми уравнениями.
Вращающаяся печь
для обжига цемента
Стекловаренная печь
Лабораторные и
модельные испытания
10

11.

Физическое моделирование
Метод сводится обычно к изучению моделей, которые отличаются от
объекта М масштабами (например, лабораторные и промышленные
мельницы).
В основе физического М лежат теория подобия и анализ
размерностей.
Необходимым условием физического М является равенство в объекте
и его модели так называемых критериев подобия, представляющих
собой определенные безразмерные комбинации различных
физических величин, оказывающих влияние на параметры объекта и
модели.
На практике обеспечить указанное условие в случае равенства
нескольких критериев подобия чрезвычайно трудно, если только не
делать модель тождественной объекту М. Поэтому используют
приближенное физическое М, при котором второстепенные процессы,
происходящие в объекте, либо не моделируются совсем, либо
моделируются приближенно.
11

12.

Достоинства физического моделирования:
возможность изучения объектов с меньшими затратами (сырья,
энергии, времени);
возможность исследования объектов, для которых физикохимическая сущность процессов мало изучена;
возможность проведения на модели измерений, слишком сложных
на объекте М.
Недостатки метода:
возможность проявления собственных свойств модели вследствие
несоответствия критериев подобия объекта и модели (например,
различные условия процесса);
необходимость применения аналогичных контрольноизмерительных приборов на модели и объекте;
относительная сложность построения физической модели, обычно
представляющей собой значительно уменьшенную копию объекта;
трудность достоверной экстраполяции результатов на другие
масштабы из-за полного отсутствия надежных критериев
достоверности масштабного перехода.
12

13.

Несмотря на недостатки, физическое М часто служит единственным
средством исследования технологических процессов (особенно мало
изученных). При этом оно во многих случаях предшествует
математическому моделированию, являясь источником
экспериментальных данных для построения и проверки
математических моделей.
13

14.

Математическое моделирование
Метод сводит исследование свойств объекта к изучению свойств
математической модели – системы уравнений, которая отражает
поведение объекта М.
Математическая модель дает возможность прогнозировать это
поведение при изменяющихся условиях функционирования объекта.
Аналогом эксперимента на модели при физическом М служит
вычислительный эксперимент, который проводят, как правило, на
ЭВМ.
К числу наиболее распространенных типов моделей относят:
стохастические,
статистические,
детерминированные.
14

15.

Стохастические модели
строят на основе вероятностных представлений о процессах в
объекте М и позволяют прогнозировать его поведение путем
вычисления функций распределения вероятностей для переменных,
характеризующих исследуемые свойства.
Важнейшая область применения стохастических моделей – М
больших систем (крупных агрегатов, процессов, производств,
предприятий и др.).
Эти модели используют для анализа функционирования объектов в
условиях случайных возмущений, для решения сложных задач
календарного планирования работы предприятия, исследования
возможных последствий непредсказуемых аварийных отказов
технологического оборудования, выявления наиболее эффективных
схем резервирования для повышения надежности производства в
целом и т.д.
15

16.

Статистические модели
строят на основе экспериментальных данных, полученных на
действующем объекте, и представляют собой соотношения, которые
связывают значения выходных и входных переменных объекта.
Вид этих соотношений обычно задается заранее; и определению
подлежат лишь значения некоторых параметров. Наиболее
распространена зависимость, задаваемая в форме многочлена
степени не более 2.
При определении параметров этих моделей используют аппарат
математической статистики, поскольку на результаты экспериментов и
измерений, как правило, накладываются случайные ошибки, а также
действие неучтенных факторов.
16

17.

В случае построения статистических моделей на основе данных,
которые найдены в так называемом пассивном эксперименте
(регистрация значений входных и выходных переменных
осуществляется без вмешательства в процесс), рассчитываемые
параметры моделей оказываются, как правило, статистически
зависимыми. Это значительно усложняет интерпретацию результатов
и ограничивает прогнозирующие возможности модели.
Более надежные данные могут быть получены при планомерном
варьировании входных переменных в желаемых пределах.
Этапы общей процедуры построения любой статистической модели:
1) расчет ее параметров;
2) проверка значимости найденных значений параметров;
3) проверка адекватности полученной модели объекту.
17

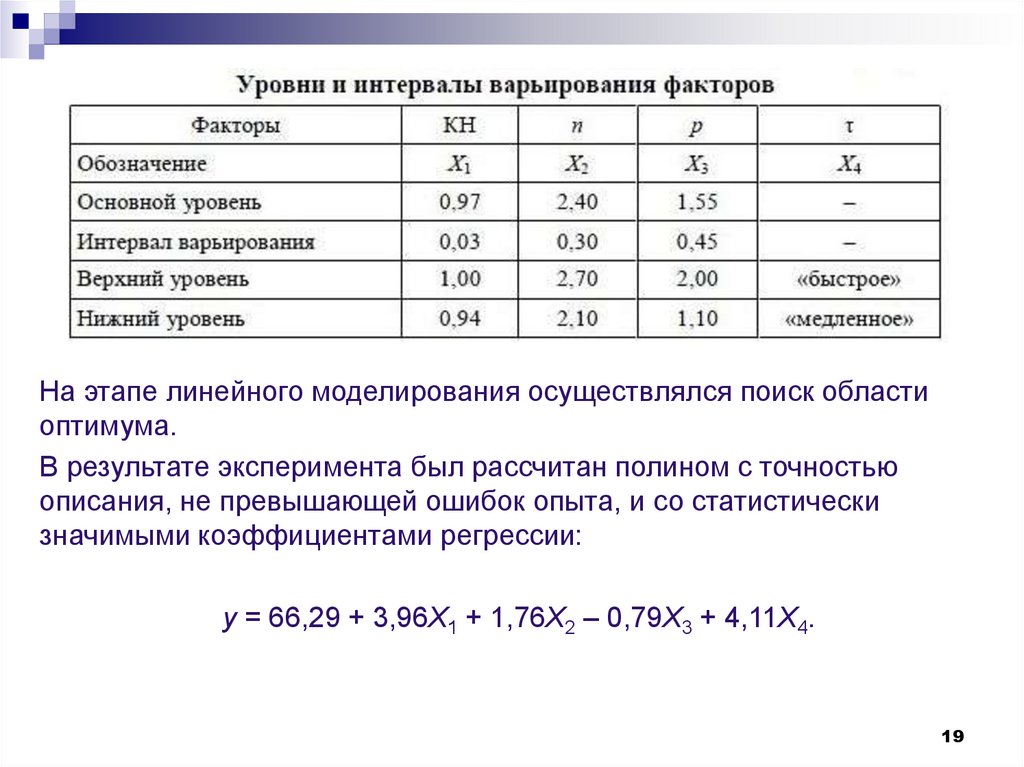
18.

Пример: установление оптимальных характеристик химического
состава сырьевой смеси и режима охлаждения цементного клинкера с
использованием методов математического планирования
эксперимента, обеспечивающих синтез максимального количества
основной фазы алита.
Функция отклика – содержание алита, обеспечивающего интенсивный
набор прочности цементного камня в первые сроки твердения в
зависимости от четырех переменных факторов:
модульных характеристик сырьевой смеси (X1 – коэффициент
насыщения (КН), X2 – силикатный модуль (p), X3 – глиноземный модуль
(n))
и режима охлаждения цементного клинкера (X4).
Факторы X1, X2, X3 являются количественными, отражают химический
состав шихты. Фактор X4 является качественным и принимает два
значения: «быстрое» и «медленное» охлаждение.
18

19.

На этапе линейного моделирования осуществлялся поиск области
оптимума.
В результате эксперимента был рассчитан полином с точностью
описания, не превышающей ошибок опыта, и со статистически
значимыми коэффициентами регрессии:
y = 66,29 + 3,96Х1 + 1,76Х2 – 0,79Х3 + 4,11Х4.
19

20.

Анализ полученного уравнения регрессии
y = 66,29 + 3,96Х1 + 1,76Х2 – 0,79Х3 + 4,11Х4.
Параметр оптимизации (содержание фазы алита в цементном
клинкере) возрастает с увеличением коэффициента насыщения
сырьевой смеси (Х1) и силикатного модуля (Х2) и уменьшением
глиноземного модуля (Х3).
Наибольшее влияние на параметр оптимизации оказывает четвертый
фактор – режим охлаждения (высокий коэффициент при четвертом
переменном Х4).
Знак «+» перед Х4 свидетельствует о необходимости применения
«быстрого» режима охлаждения цементного клинкера.
20

21.

Дальнейшая оптимизация значений факторов – КН и n при
фиксированном факторе Х3 (глиноземный модуль) и постоянном
режиме охлаждения – «быстром».
При этом была расширена исследуемая область и принят больший
интервал варьирования факторов: коэффициент насыщения – 0,05
и силикатный модуль – 0,4.
По результатам испытаний рассчитано уравнение второго порядка
со статистически значимыми коэффициентами:
y = 60,56 + 0,71Х1 + 0,58Х2 + 2,07Х12 + 0,87Х22.
-> большее влияние Х1 по сравнению с Х2.
21

22.

Функция отклика
содержания алита
в зависимости
от величины КН и n
сырьевой смеси
22

23.

Для проверки значимости параметров и адекватности модели обычно
используют статистические критерии проверки гипотез. Если какойлибо параметр модели при проверке оказывается незначимым, то его
значение в уравнениях модели считают равным нулю, что приводит к
упрощению модели.
Численное значение критерия адекватности само по себе еще не
позволяет сделать заключение об адекватности модели и должно
быть обязательно соотнесено со всеми статистической оценками
измерений на объекте М.
Если в результате проверки адекватности модель оказывается
неадекватной, это означает, что какие-то существенные входные
переменные, оказались не включенными в модель или точность
экспериментальных данных недостаточна для установления искомой
зависимости.
23

24.

Достоинства статистических моделей:
возможность применения к объектам с неизвестными механизмами
происходящих в них процессов, а также в случае больших систем,
детальное описание которых вызывает серьезные трудности.
Недостатки:
сложность обобщения получаемых результатов даже при изучении
однотипных объектов, невозможность обоснованной экстраполяции
свойств модели за пределы измеренной области изменения входных
переменных, трудность построения таких моделей для
нестационарных объектов с большим временным запаздыванием
реакции на входные возмущения.
Важнейшие области применения статистических моделей:
– планирование оптимальных условий экспериментов и описание
функционирования отдельных аппаратов или участков производства
для решения сложных задач управления и оптимизации.
24

25.

Детерминированные модели
строят на основе математически выраженных закономерностей,
описывающих физико-химические процессы в объекте М. Они
позволяют однозначно находить значения переменных, которые
характеризуют представляющие интерес свойства объекта, для
любой заданной совокупности значений входных переменных и
конструктивных параметров объектов М и являются основой для
решения задач масштабного перехода.
Для вычислительных экспериментов с детерминированными
моделями реальных объектов, как правило, требуются средства
вычислительной техники; при этом особое внимание уделяются
разработке эффективных алгоритмов решения системы уравнений
математического описания.
25

26.

Для большинства процессов химической технологии характерно
наличие взаимодействующих потоков веществ, в которых возможны
также химические превращения. Поэтому в основу математического
описания, как правило, кладут уравнения балансов масс и энергии в
потоках.
При наличии в процессе нескольких потоков веществ, а также
потоков, состоящих из нескольких фаз, для каждого потока и для
каждой фазы обычно записывают свои уравнения.
Уравнения балансов масс и энергии включают источники вещества и
энергии в потоках, интенсивность которых определяется конкретными
физико-химическими процессами, происходящими в объекте.
Поэтому в состав математического описания входят также уравнения
для скоростей химических реакций, массо- и теплообмена и др.
26

27.

Кроме того, математическое описание включает теоретические,
полуэмпирические или эмпирические соотношения, характеризующие
различные зависимости, например теплоемкости от состава потока,
коэффициента массопередачи от скоростей потоков фаз и т.д.
При построении детерминированной модели большое значение имеет
разумное сочетание требуемой сложности модели с допустимыми
упрощениями. Слишком сложное математическое описание,
учитывающее множество, возможно, второстепенных факторов и
явлений, может оказаться неприемлемым из-за необходимости
выполнения огромного объема вычислений при решении входящих в
него уравнений. Наоборот, слишком упрощенное описание может
привести к принципиально неправильным выводам о свойствах
объекта М.
27

28.

Принято различать стационарные и нестационарные модели, в
которых параметры соответственно не изменяются и изменяются во
времени.
Кроме того, принято выделять модели с распределенными и
сосредоточенными параметрами, соответственно изменяющимися и
не изменяющимися в пространстве.
Основу описания стационарных моделей с сосредоточенными
параметрами составляют системы, в которых отсутствуют
дифференциальные уравнения, поскольку переменные модели не
зависят от пространственных координат и времени.
Дифференциальные уравнения используют в моделях для описания
нестационарных режимов в объектах при допущении
сосредоточенности параметров или для описания стационарных
режимов в объектах с параметрами, распределенными только по
одной координате. Это отвечает зависимости переменных модели от
одной пространственной координаты либо от времени.
28

29.

При построении алгоритма, как правило, используют специфические
особенности решаемой задачи.
Пример:
при составлении теплового баланса теплотехнического агрегата
используют уравнения материальных балансов горения компонентов
топлива; уравнения основного теплового баланса и уравнения для
различного рода потерь тепла. Последние могут не рассчитываться, а
приниматься установленным образом.
Идентификация моделей
При неудовлетворительной адекватности априорно построенной
модели уточняют заданные приближенно значения параметров, вид
некоторых зависимостей, включенных в состав математического
описания.
Методы идентификации моделей разнообразны. Выбор подходящего
метода в каждом конкретном случае определяется объектом
моделирования и имеющимися в распоряжении исследователя
ресурсами.
29

30.

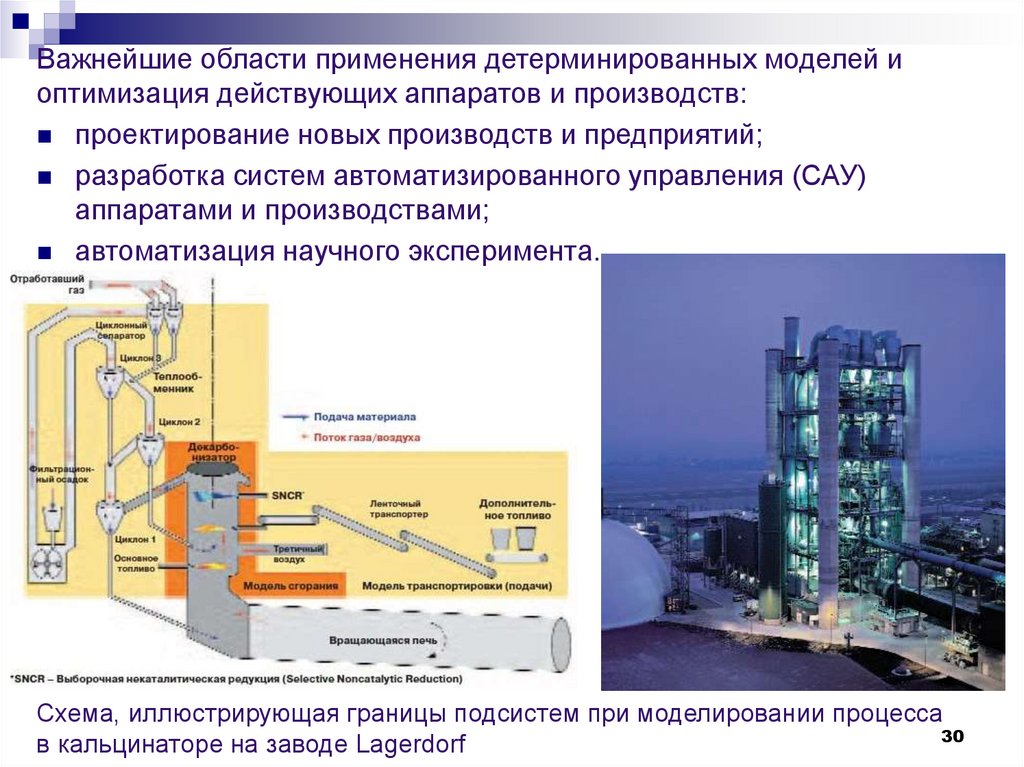
Важнейшие области применения детерминированных моделей и
оптимизация действующих аппаратов и производств:
проектирование новых производств и предприятий;
разработка систем автоматизированного управления (САУ)
аппаратами и производствами;
автоматизация научного эксперимента.
Схема, иллюстрирующая границы подсистем при моделировании процесса
30
в кальцинаторе на заводе Lagerdorf

31.

Моделирование процесса
в кальцинаторе на заводе
Lagerdorf
31

32.

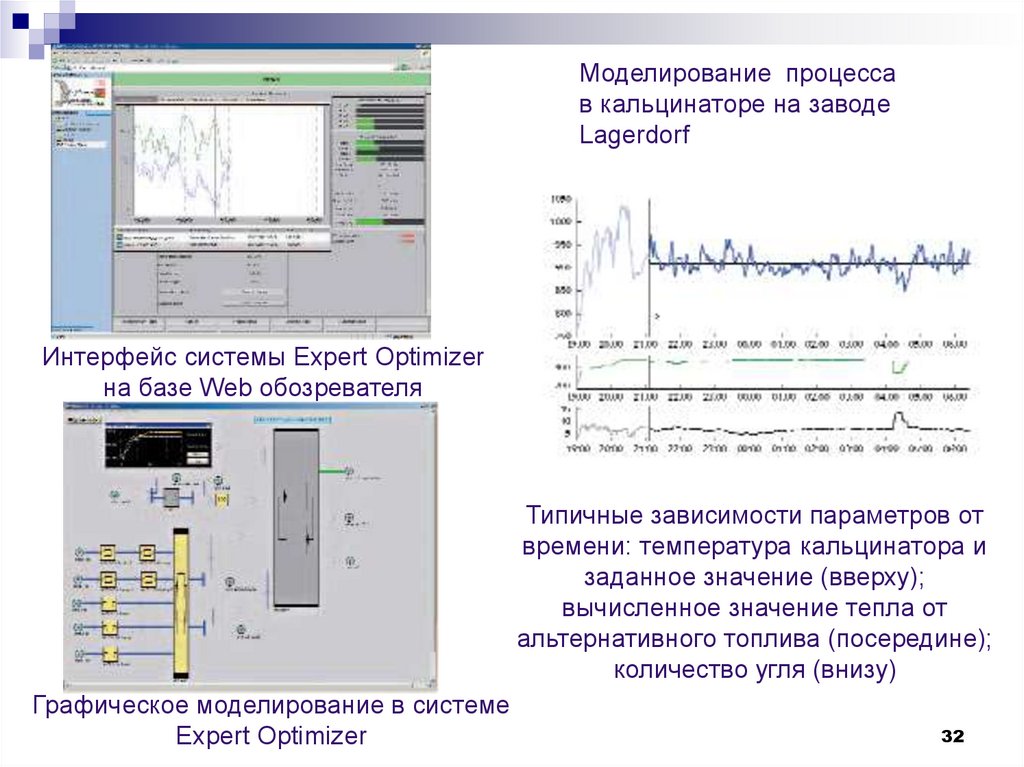
Моделирование процесса
в кальцинаторе на заводе
Lagerdorf
Интерфейс системы Expert Optimizer
на базе Web обозревателя
Типичные зависимости параметров от
времени: температура кальцинатора и
заданное значение (вверху);
вычисленное значение тепла от
альтернативного топлива (посередине);
количество угля (внизу)
Графическое моделирование в системе
Expert Optimizer
32

33.

Результаты моделирования на заводе Lagerdorf
Разработана прогнозирующая модель для системы управления
температурой кальцинатора.
Алгоритм был реализован с использованием ПО Expert Optimizer.
Достигнутые результаты показывают, что в этом случае
обеспечивается значительно лучшее качество управления, чем при
ручной работе оператора. Система Expert Optimizer позволяет
непрерывно вычислять и производить необходимые изменения
регулируемых параметров.
Качество управления, достигнутое на заводе Lagerdorf, делает
возможным:
эксплуатировать установку при более низких средних
температурах кальцинатора без отрицательного влияния на
требуемое качество клинкера;
стабилизировать процесс с помощью системы управления;
позволяет защитить оборудование (т. е. огнеупорной футеровки) от
перегрева.
33

34.

Основные этапы моделирования
1 этап. ПОСТАНОВКА ЗАДАЧИ
1. Описание задачи:
задачи, в которых требуется исследовать, как изменятся
характеристики объекта при некотором воздействии на него.
Такую постановку задачи принято называть «что будет, если?..»;
задачи, имеющие следующую формулировку: какое надо
произвести воздействие на объект, чтобы его параметры
удовлетворяли некоторому заданному условию? Такую
постановку задачи называют «как сделать, чтобы?..»
34

35.

2. Цель моделирования
(от выбранной цели зависит, какие характеристики исследуемого
объекта считать существенными, а какие отбросить).
«что будет, если?..» - определение последствий воздействия на
объект и принятие правильного решения.
«как сделать, чтобы?..» - создание объектов с заданными свойствами.
3. Формализация задачи
(формализм – строгий порядок).
Формализацию проводят в виде поиска ответов на вопросы,
уточняющие общее описание задачи.
35

36.

2 этап. РАЗРАБОТКА МОДЕЛИ
1. Информационная модель
Выбор наиболее существенных данных при формировании
информационной модели и ее сложность определяются целью
моделирования.
2. Компьютерная модель
(модель, реализованная средствами программной среды)
Примеры: набор текста, составленный алгоритм, программа для
расчета и др.
36

37.

3 этап. КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ
1. План эксперимента и тестирование модели
(должен четко отражать последовательность работы с моделью)
Тестирование – процесс проверки правильности построения модели.
Тест – набор исходных данных, позволяющий определить
правильность построения модели.
2. Проведение исследования
Если модель правильна, переходят к проведению исследования.
37

38.

4 этап. АНАЛИЗ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ
Этот этап решающий – либо исследование продолжается, либо
заканчивается.
Если результаты не соответствуют целям поставленной задачи,
значит, на предыдущих этапах были допущены ошибки.
Если такие ошибки выявлены, то требуется корректировка модели, то
есть возврат к одному из предыдущих этапов.
Процесс повторяется до тех пор, пока результаты эксперимента не
будут отвечать целям моделирования.
Выбор типа
вывода результатов
расчетов
38

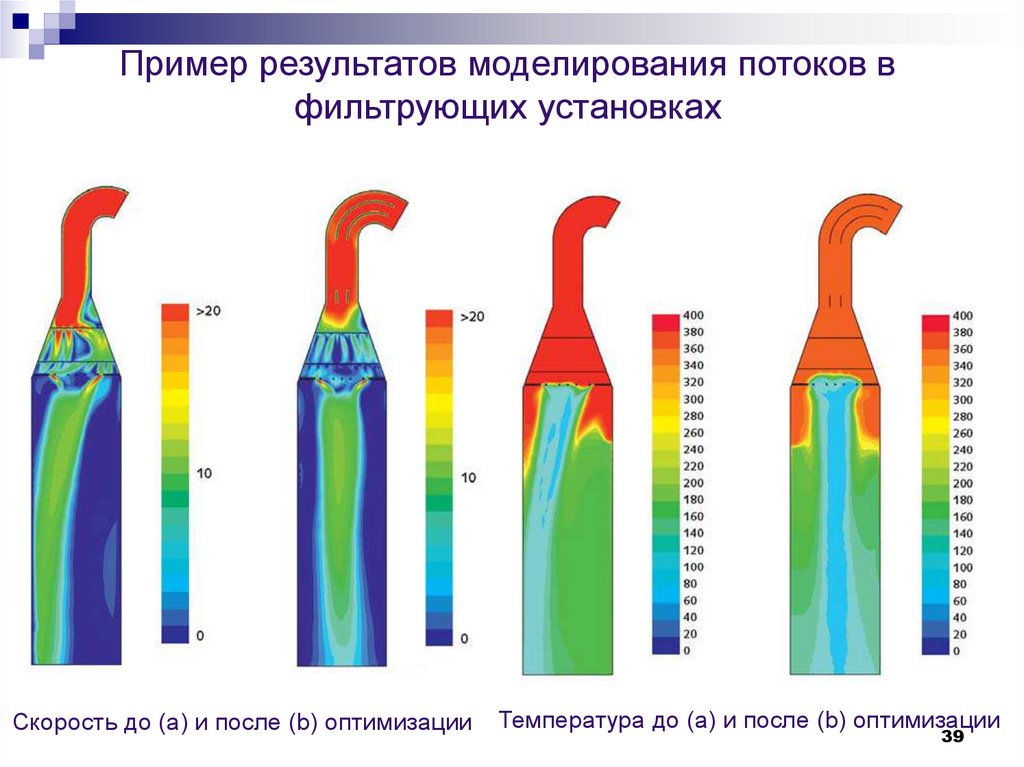
39.

Пример результатов моделирования потоков в
фильтрующих установках
Скорость до (a) и после (b) оптимизации
Температура до (a) и после (b) оптимизации
39