Понятие предела функции

1. Понятие предела функции

ГБПОУ МО СП СЭТ
Преподаватель математики
Крылова И.К.

2. Тип занятия – комбинированный урок, включающий в себя повторение пройденного материала, применение знаний и умений на практике,

закрепление
изученного.
Цели занятия:
Образовательные:
повторить понятие предела числа,
функции;
научиться вычислять пределы функции;
систематизировать полученные знания,
активизировать самоконтроль,
взаимоконтроль.
предела

3. Развивающие:

развивать умения анализировать собственные
потребности,
выбора
соответствующей
позиции на каждый этап урока с
последующим анализом своей деятельности.
Воспитательные:
воспитывать:
- познавательный интерес к математике;
- информационную культуру и культуру общения;
- самостоятельность, способность к коллективной
работе.

4. 1. Организация занятия

Мобилизация учебной деятельности учащихся:
доброжелательный настрой учителя и
учащихся, быстрое включение класса в
деловой ритм, организация внимания всех
учащихся
2. Проверка знаний учащихся по теме:
«Понятие
функции,
понятие
предела
функции в точке, основные теоремы о
пределах».
Методы проверки: устный опрос, диалоговые
технологии.

5. План:

I. Повторение материала.
1. Понятие функции.
2. Предел функции в точке.
3. Основные теоремы о пределах.
4. Замечательные пределы и формулы в
помощь для вычисления пределов.
II. Закрепление материала.
1. Решение простых пределов.
2. Раскрытие неопределённостей.

6. I. Повторение материала.

1. Понятие функции.
• Определение. Если каждому значению х
числового множества X по правилу f
соответствует единственное число множества Y,
то говорят, что на числовом множестве X
задана функция у = f(x), значения х
определяются множеством значений, входящих
в область определения функции (Х) .
• В этом случае х называется аргументом, а у значением функции. Множество X называется
областью
определения
функции,
Y
множеством значений функции.

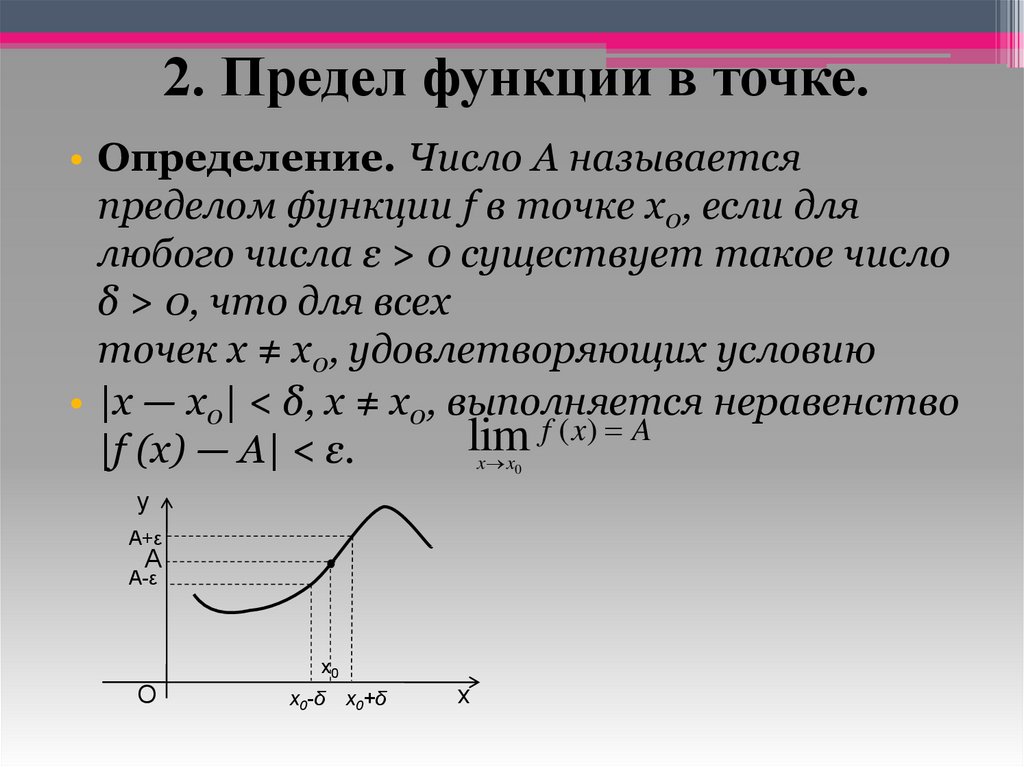
7. 2. Предел функции в точке.

• Определение. Число А называется
пределом функции f в точке x0, если для
любого числа ε > 0 существует такое число
δ > 0, что для всех
точек х ≠ x0, удовлетворяющих условию
• |х — x0| < δ, x ≠ x0, выполняется неравенство
f ( x) A
lim
|f (x) — A| < ε.
x x
0
у
А+ε
А
А-ε
О
х0
х0-δ
х0+δ
х

8.

• Все основные элементарные функции:
постоянные, степенная функция (хα),
показательная функция (ax),
тригонометрические функции
(sinx, cosx, tgx и ctgx) и обратные
тригонометрические функции
(arcsinx, arccosx, arctgx и arcctgx) во всех
внутренних точках своих областей
определения имеют пределы, совпадающие с
их значениями в этих точках.

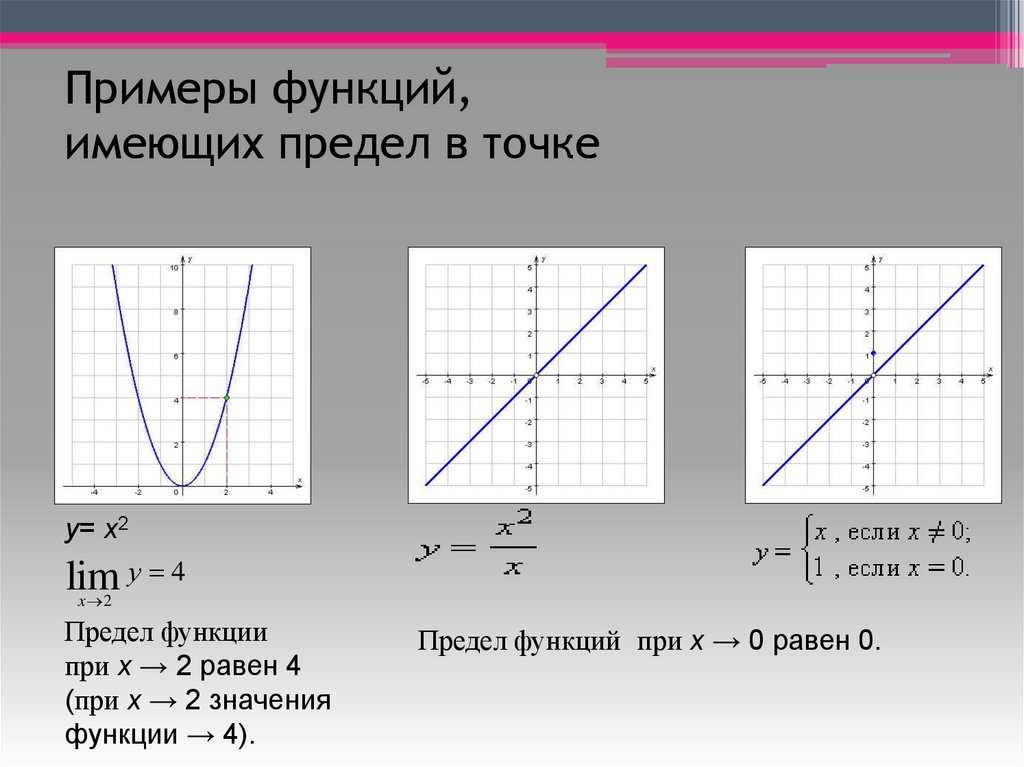
9. Примеры функций, имеющих предел в точке

у= x2
lim у 4
x 2
Предел функции
при x → 2 равен 4
(при x → 2 значения
функции → 4).
Предел функций при x → 0 равен 0.

10.

Примеры функций,
не имеющих предел в точке
у
у
у
А
1
О
х
-1
О
а
х
О
а
х

11. 3. Основные теоремы о пределах.

Если функции f (x) и g (x) имеют конечные пределы в точке a,
причем
То
если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a.

12. 4. Замечательные пределы и формулы в помощь для вычисления пределов.

• Первый замечательный предел
sin x
1
lim
x
x 0
• Второй замечательный предел
1 x
(
1
) e
lim
x
x

13. формулы в помощь

14. II. Закрепление материала. 1. Решение простых пределов.

Вычисление предела функции в точке
1. Сначала просто пытаемся подставить число в функцию
lim ( x 5x 8) 9 15 8 2
2
x 3
Найдем
x2 5x 8
lim
.
2
x 3 x
x 4
Предел числителя
lim ( x 2 5x 8) 9 15 8 2
x 3
Предел знаменателя
lim ( x 2 x 4) 9 3 4 10
x 3
.
Используя теорему о пределе частного, получим
lim ( x 2 5 x 8)
x 5x 8
2
1
x 3
.
2
x 3 x 2 x 4
10 5
lim ( x x 4)
2
lim
x 3

15.

2. Найдем
x 2 5x 8
lim
.
x 3
x 3
Предел числителя
lim ( x 2 5x 8) 9 15 8 2
x 3
Предел знаменателя равен нулю, поэтому теорему о пределе
частного применять нельзя.
Величина 1/(x-3) является бесконечно большой величиной при
x→3.
Тогда
x 2 5x 8
lim
.
x 3
x 3

16. Физкультминутка -3 мин

• Дружно с вами мы считали и про пределы
рассуждали.
• А теперь вы дружно встали свои косточки размяли.
• На счёт раз в кулак сожмём, на счёт два в локтях
сожмём.
• На счёт три – прижмём к плечам, на четыре к
небесам.
• Хорошо прогнулись и друг другу улыбнулись.
• Про пятёрку не забудем – добрыми всегда мы
будем.
• На счёт шесть прошу всех сесть.
• Математика вы и я вместе дружная 7-я.

17. 2. Раскрытие неопределенности

• При нахождении предела
неопределенностями вида
иногда
0
0
0
, , ( ), (1 ), (0 ), (0 )( ).
0
• Отыскание предела в таких
раскрытием неопределенности.
сталкиваются
случаях
с
называется
1) Для того, чтобы раскрыть неопределенность ∞/∞ необходимо
разделить числитель и знаменатель на х в старшей степени.
Разделим числитель и знаменатель на х2

18.

2) В следующем примере разделим числитель и знаменатель на х4

19.

3) В следующем примере разделим числитель и знаменатель на х2
подразумевается не деление на ноль (делить на ноль нельзя), а деление
на бесконечно малое число.
ВЫВОД: Таким образом, при раскрытии
неопределенности может получиться конечное число, ноль
или бесконечность.

20.

:
Раскрытие неопределенности вида 0/0
Вычислить предел
Сначала попробуем подставить -1 в дробь:
В данном случае получена так называемая неопределенность 0/0
Общее правило: если в числителе и знаменателе находятся
многочлены, и имеется неопределенность вида 0/0, то для ее
раскрытия нужно разложить числитель и знаменатель на
множители.
Очевидно, что можно сократить на (х+1)
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

21.

Метод умножения числителя и знаменателя на сопряженное выражение
Найти предел
Сначала пробуем подставить 3 в выражение под знаком предела это первое,
что нужно выполнять для ЛЮБОГО предела.
Получена неопределенность вида 0/0 ,
которую нужно устранять
Когда в числителе (знаменателе) находится разность корней (или корень минус какоенибудь число), то для раскрытия неопределенности используют метод умножения
числителя и знаменателя на сопряженное выражение.

22.

23. Самостоятельная работа с взаимопроверкой 5 мин

2 x 2 3x 1
5) lim 4 x 2 2 x 5
ч

24. Инструкция по проверке

• 5 правильно решённых примеров- 5 баллов
• 4 правильно решённых примеров – 4 балла
• 3 правильно решённых примеров – 3 балла
• Менее 3 правильно решённых примеров – 0
баллов.

25. Подведение итогов урока

• Итак, ребята, на данном уроке мы повторили
понятие функции, понятие предела функции,
закрепили методы решения при раскрытии
неопределённостей для вычисления
пределов. Есть ли у вас вопросы?
• Проверте, все ли баллы вы себе проставили в
технологическую карту и сдайте для
проставления оценки в журнал.

26. Домашнее задание раздается на карточках каждому ученику.

27.

•СПАСИБО ЗА УРОК!