Similar presentations:
Sztuczna Inteligencja
1.
Sztuczna Inteligencja(laboratorium 2)
Katedra Systemów Ekspertowych i Sztucznej Inteligencji
Wyższa Szkoła Informatyki i Zarządzania w Rzeszowie
2.
PrzypomnienieReguły decyzyjne są jednym z najpopularniejszych
formalizmów reprezentacji wiedzy, stosowanym w
uczeniu maszynowym oraz odkrywaniu wiedzy z
danych.
Reguła decyzji składa się z części warunkowej oraz
części decyzyjnej, w której podaje decyzję właściwą
dla sytuacji, gdy spełnione są określone warunki.
jeżeli są spełnione określone warunki to decyzja
3.
Ogólna postać regułyJeżeli P to Q
If P Then Q
P – część warunkowa (przesłanka)
Q – część decyzyjna (konkluzja)
Część warunkowa P może być koniunkcją warunków elementarnych w, i jest wtedy zapisywana w
postaci: P = w1 ^w2 …^wk, gdzie k jest liczbą użytych warunków. P nazywane jest także złożeniem
warunków lub kompleksem.
4.
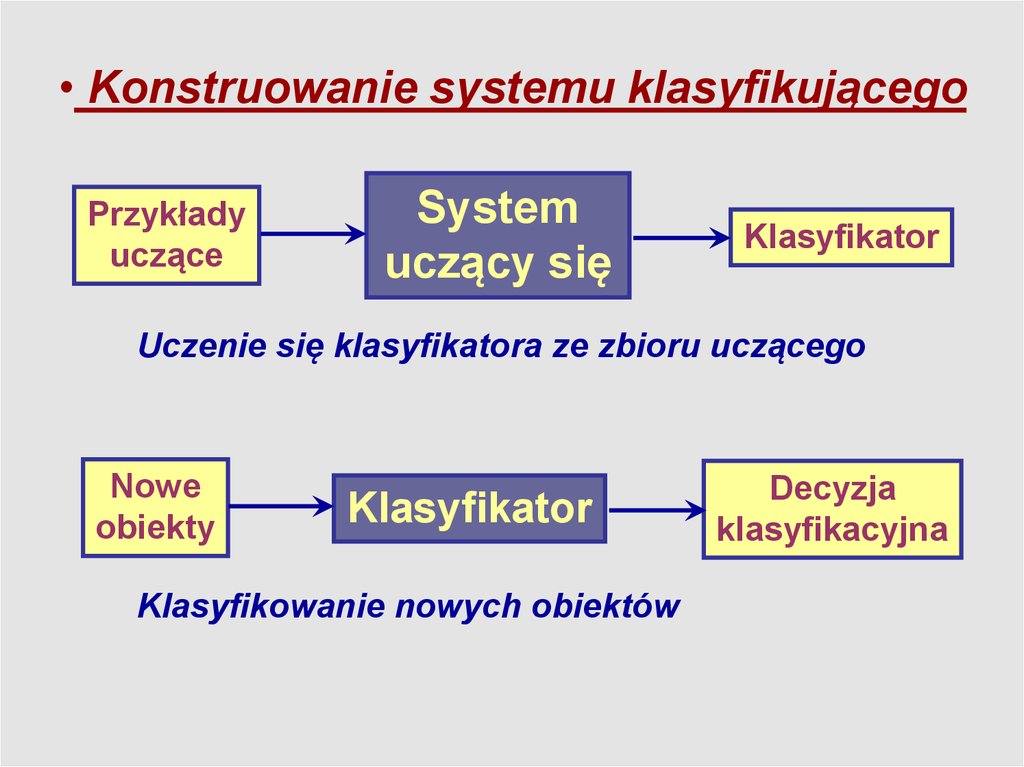
• Konstruowanie systemu klasyfikującegoPrzykłady
uczące
System
uczący się
Klasyfikator
Uczenie się klasyfikatora ze zbioru uczącego
Nowe
obiekty
Klasyfikator
Klasyfikowanie nowych obiektów
Decyzja
klasyfikacyjna
5. Algorytmy generowania reguł
GTS
LEM2
CN2
Rodzina algorytmów AQ
INLEN
MODLEM
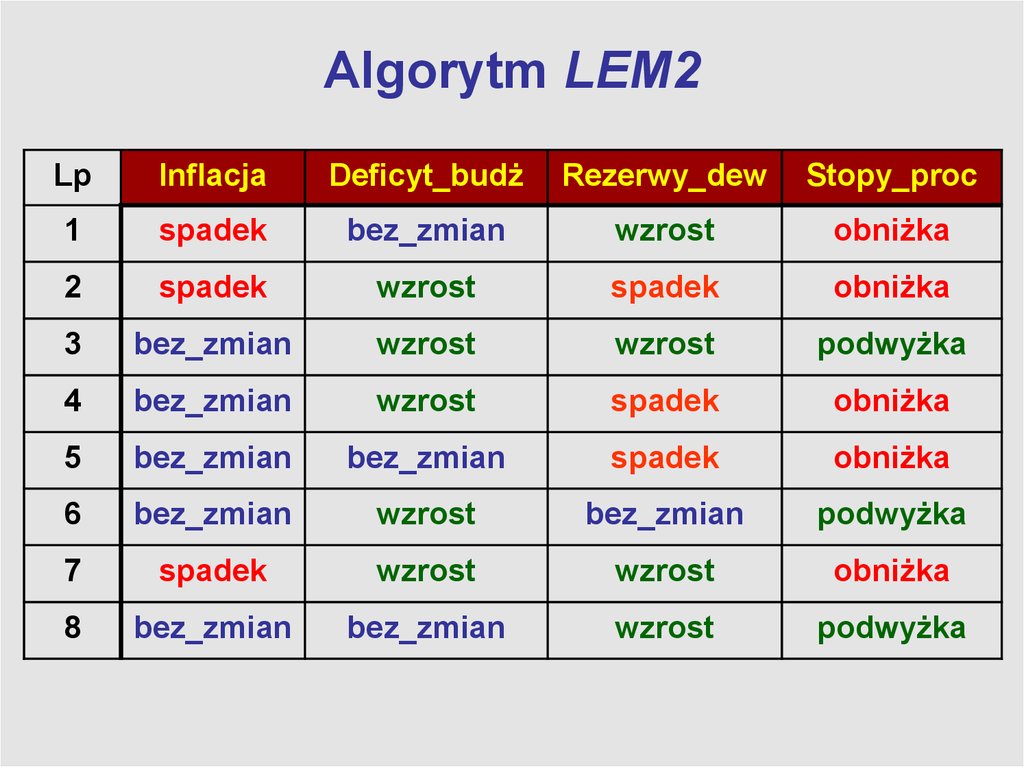
6. Algorytm LEM2
LpInflacja
Deficyt_budż
Rezerwy_dew
Stopy_proc
1
spadek
bez_zmian
wzrost
obniżka
2
spadek
wzrost
spadek
obniżka
3
bez_zmian
wzrost
wzrost
podwyżka
4
bez_zmian
wzrost
spadek
obniżka
5
bez_zmian
bez_zmian
spadek
obniżka
6
bez_zmian
wzrost
bez_zmian
podwyżka
7
spadek
wzrost
wzrost
obniżka
8
bez_zmian
bez_zmian
wzrost
podwyżka
7. Algorytm LEM2
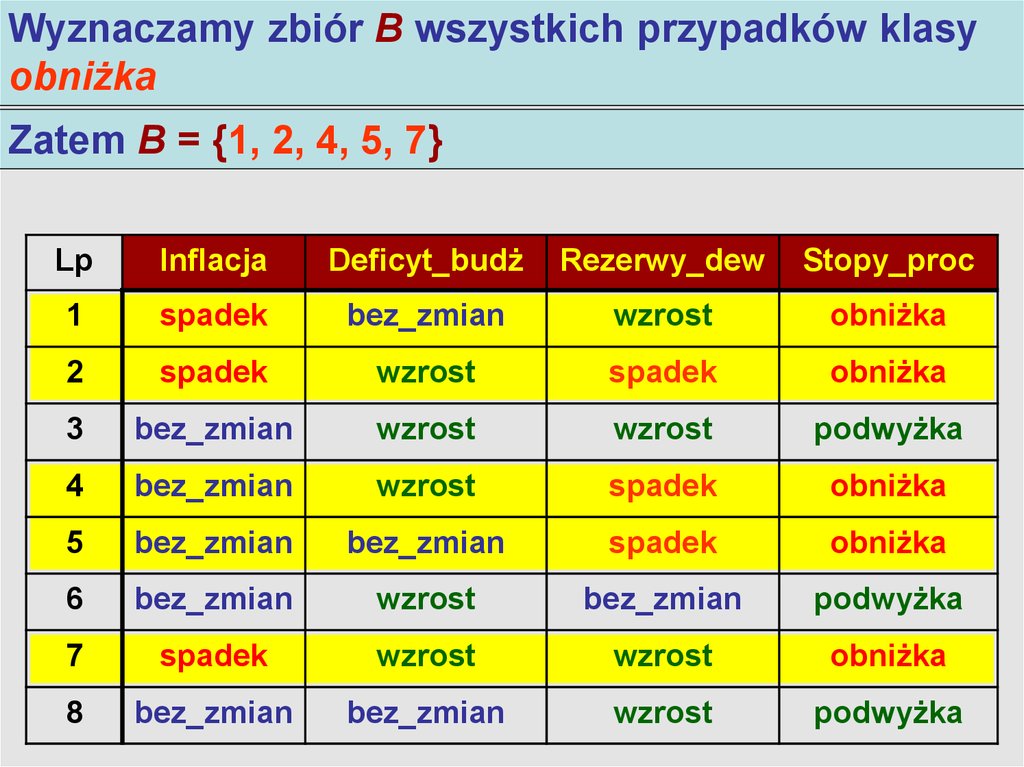
Wyznaczamy zbiór B wszystkich przypadków klasyAlgorytm LEM2
obniżka
Zatem B = {1, 2, 4, 5, 7}
Lp
Inflacja
Deficyt_budż
Rezerwy_dew
Stopy_proc
1
spadek
bez_zmian
wzrost
obniżka
2
spadek
wzrost
spadek
obniżka
3
bez_zmian
wzrost
wzrost
podwyżka
4
bez_zmian
wzrost
spadek
obniżka
5
bez_zmian
bez_zmian
spadek
obniżka
6
bez_zmian
wzrost
bez_zmian
podwyżka
7
spadek
wzrost
wzrost
obniżka
8
bez_zmian
bez_zmian
wzrost
podwyżka
8. Algorytm LEM2
Wyznaczamy zbiór T(G) wszystkich możliwych parAlgorytm
LEM2 ze zbioru B
atrybut-wartość spośród
przypadków
Zatem T(G) = {(Inflacja, spadek), (Inflacja,
bez_zmian), (Deficyt_budż, bez_zmian),
(Deficyt_budż, wzrost), (Rezerwy_dew, wzrost),
Lp
Inflacja
Deficyt_budż Rezerwy_dew Stopy_proc
(Rezerwy_dew, spadek)}
1
spadek
bez_zmian
wzrost
obniżka
2
spadek
wzrost
spadek
obniżka
3
bez_zmian
wzrost
wzrost
podwyżka
4
bez_zmian
wzrost
spadek
obniżka
5
bez_zmian
bez_zmian
spadek
obniżka
6
bez_zmian
wzrost
bez_zmian
podwyżka
7
spadek
wzrost
wzrost
obniżka
8
bez_zmian
bez_zmian
wzrost
podwyżka
9. Algorytm LEM2
Zakładamy wstępnie, żeB = G = {1, 2, 4, 5,Algorytm
7} oraz π =LEM2
Ø
Ponadto:
[(Inflacja, spadek)] = {1, 2, 7}
[(Inflacja, bez_zmian)] = {3, 4, 5, 6, 8}
Lp
Inflacja
Deficyt_budż
Rezerwy_dew
[(Deficyt_budż,
5, 8}
1
spadek bez_zmian)]
bez_zmian = {1,
wzrost
[(Deficyt_budż,
wzrost)]
= {2, 3, spadek
4, 6, 7}
2
spadek
wzrost
Stopy_proc
obniżka
obniżka
3
bez_zmian wzrost)]
wzrost = {1, 3, wzrost
podwyżka
[(Rezerwy_dew,
7, 8}
[(Rezerwy_dew,
5}
4
bez_zmian spadek)]
wzrost = {2, 4,spadek
obniżka
Zatem T(G) = {(Inflacja, bez_zmian), (Deficyt_budż,
5
bez_zmian
bez_zmian
spadek
obniżka
wszystkich
par wybieramy
te, które
mają
Spośród
tych
3 par
wybieramy
te,
które
mają
bez_zmian),
(Deficyt_budż,
wzrost),
(Rezerwy_dew,
największą
część
wspólną
ze zbiorem
G: podwyżka
moc tzn.
pokrywają
najmniejszą
liczbę
6
bez_zmian
wzrost
bez_zmian
wzrost),
(Rezerwy_dew,
spadek)}
(Inflacja,
spadek),
wzrost) oraz
przypadków
z innej(Deficyt_budż,
kategorii
(podwyżka),
czyli
Ponieważ
spełniony
jest warunek
7
spadek
wzrost
wzrost
obniżka
(Rezerwy_dew,
spadek)
pokrywają
po 3 przypadki
(Inflacja,
spadek),
(Rezerwy_dew,
spadek),
które
[(Inflacja,
spadek)]
= {1, 2,
7} Bwzrost
8
bez_zmian
bez_zmian
podwyżka
mają taką
samą moc,
z nich pierwszą.
można
utworzyć
regułęwybieramy
R1
10.
Reguła 1:JEŻELI Inflacja JEST spadek
TO Stopy_proc JEST obnizka
11. Algorytm LEM2
π = π {T} = Ø {1, 2, 7} = {1, 2, 7}Algorytm
G = B – [T] = {1, 2,
4, 5, 7} – {1,LEM2
2, 7} = {4, 5}
Ponadto:
[(Inflacja, bez_zmian)] = {3, 4, 5, 6, 8}
Lp
Inflacja bez_zmian)]
Deficyt_budż =Rezerwy_dew
[(Deficyt_budż,
{1, 5, 8}
[(Deficyt_budż,
= {2, 3, 4,
6, 7}
1
spadek wzrost)]
bez_zmian
wzrost
2
spadek
wzrost = {1, 3,spadek
[(Rezerwy_dew,
wzrost)]
7, 8}
3
bez_zmian spadek)]
wzrost = {2, 4,wzrost
[(Rezerwy_dew,
5}
Stopy_proc
obniżka
obniżka
podwyżka
4
bez_zmian
wzrost
spadek
obniżka
Zatem
T(G) = {(Inflacja,
bez_zmian),
(Deficyt_budż,
5
bez_zmian
bez_zmian
spadek
wszystkich
par wybieramy
te, które
mają
Spośród
tych
2 par
wybieramy
tą,
która
ma obniżka
bez_zmian),
(Deficyt_budż,
wzrost),
(Rezerwy_dew,
największą
część
wspólną
ze zbiorem
6
bez_zmian
wzrost
bez_zmianG: liczbę
podwyżka
moc tzn.
pokrywa
najmniejszą
wzrost)}
(Deficyt_budż,
wzrost)
oraz
(Rezerwy_dew,
spadek)
przypadków
z innej
kategorii
(podwyżka),
czyli
Ponieważ
spełniony
jest
warunek
7
spadek
wzrost
wzrost
obniżka
pokrywają
oba
przypadki
{4,
5} 5} B podwyżka
wybieramy
(Rezerwy_dew,
spadek).
[(Rezerwy_dew,
8
bez_zmian spadek)]
bez_zmian= {2, 4,wzrost
można utworzyć regułę R2
12.
Reguła 1:JEŻELI Inflacja JEST spadek
TO Stopy_proc JEST obnizka
Reguła 2:
JEŻELI Rezerwy_dew JEST spadek
TO Stopy_proc JEST obnizka
π = π {T} = {1, 2, 7} {4, 5} = {1, 2, 4, 5, 7}
G = B – π = {1, 2, 4, 5, 7} – {1, 2, 4, 5, 7} = Ø
Ponieważ G = Ø zatem powyższe reguły pokrywają
wszystkie przypadki z kategorii obniżka, teraz należy
znaleźć reguły pokrywające następną kategorię
podwyżka
13. Algorytm LEM2
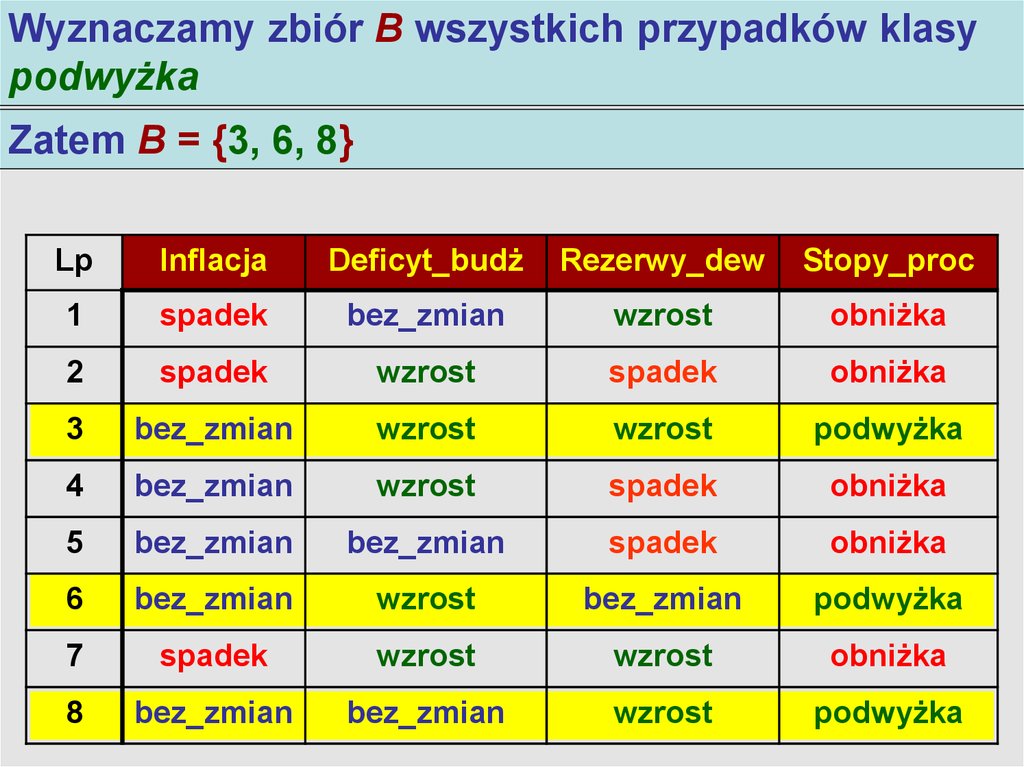
Wyznaczamy zbiór B wszystkich przypadków klasyAlgorytm LEM2
podwyżka
Zatem B = {3, 6, 8}
Lp
Inflacja
Deficyt_budż
Rezerwy_dew
Stopy_proc
1
spadek
bez_zmian
wzrost
obniżka
2
spadek
wzrost
spadek
obniżka
3
bez_zmian
wzrost
wzrost
podwyżka
4
bez_zmian
wzrost
spadek
obniżka
5
bez_zmian
bez_zmian
spadek
obniżka
6
bez_zmian
wzrost
bez_zmian
podwyżka
7
spadek
wzrost
wzrost
obniżka
8
bez_zmian
bez_zmian
wzrost
podwyżka
14. Algorytm LEM2
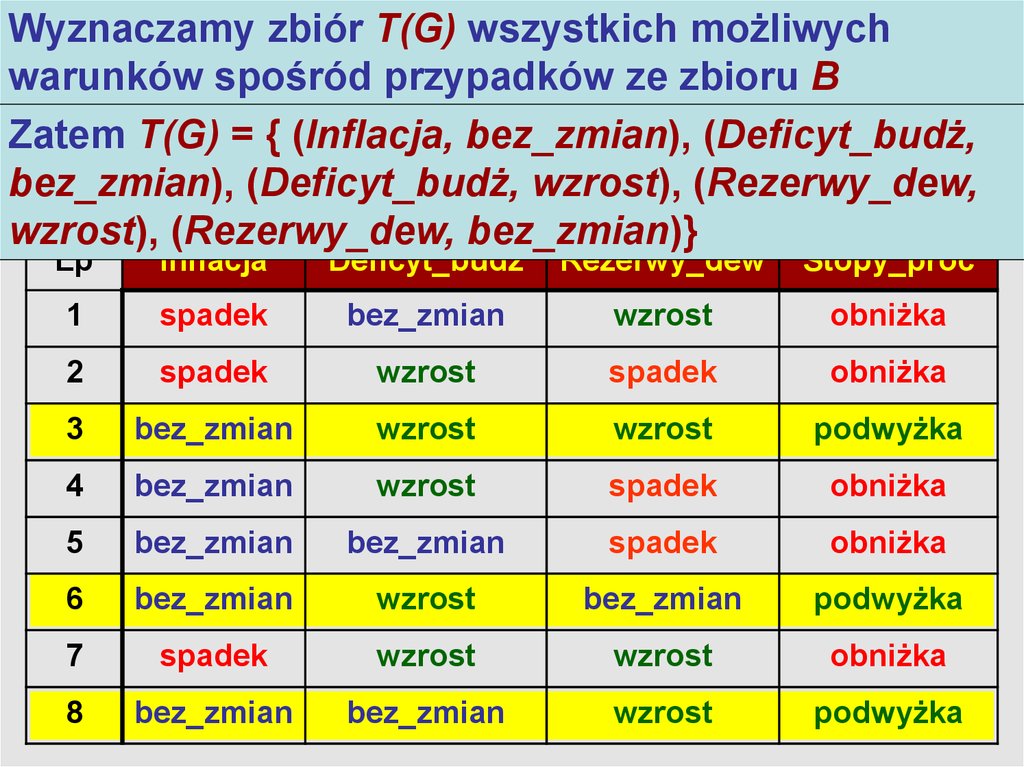
Wyznaczamy zbiór T(G) wszystkich możliwychAlgorytm
LEM2
warunków spośród
przypadków
ze zbioru B
Zatem T(G) = { (Inflacja, bez_zmian), (Deficyt_budż,
bez_zmian), (Deficyt_budż, wzrost), (Rezerwy_dew,
wzrost), (Rezerwy_dew, bez_zmian)}
Lp
Inflacja
Deficyt_budż
Rezerwy_dew
Stopy_proc
1
spadek
bez_zmian
wzrost
obniżka
2
spadek
wzrost
spadek
obniżka
3
bez_zmian
wzrost
wzrost
podwyżka
4
bez_zmian
wzrost
spadek
obniżka
5
bez_zmian
bez_zmian
spadek
obniżka
6
bez_zmian
wzrost
bez_zmian
podwyżka
7
spadek
wzrost
wzrost
obniżka
8
bez_zmian
bez_zmian
wzrost
podwyżka
15. Algorytm LEM2
Zakładamy wstępnie żeB = G = {3, 6, 8} Algorytm
oraz π = Ø
LEM2
Ponadto:
[(Inflacja, bez_zmian)] = {3, 4, 5, 6, 8}
Lp
Inflacja bez_zmian)]
Deficyt_budż =Rezerwy_dew
[(Deficyt_budż,
{1, 5, 8}
[(Defizyt_budż,
= {2, 3, 4,
6, 7}
1
spadek wzrost)]
bez_zmian
wzrost
2
spadek
wzrost
[(Rezerwy_dew,
wzrost)]
= {1, 3,spadek
7, 8}
3
bez_zmian bez_zmian)]
wzrost
wzrost
[(Rezerwy_dew,
= {6}
Stopy_proc
obniżka
obniżka
podwyżka
4
bez_zmian
wzrost
spadek
obniżka
8
bez_zmian
bez_zmian
wzrost
podwyżka
Spośród
wszystkich
warunków
wybieramy
te,
które
5
bez_zmian
bez_zmian
spadek
obniżka
pokrywają największą liczbę przypadków z kategorii
6
bez_zmian
wzrost
bez_zmian
podwyżka
podwyżka:
7
spadek
wzrost
[(Inflacja,
bez_zmian)]
pokrywa 3wzrost
przypadki obniżka
16. Algorytm LEM2
Ponieważ warunek [(Inflacja, bez_zmian)] pokrywaLEM2
przypadki 3, 6, 8 Algorytm
z klasy podwyżka
oraz przypadki 4,
5 z klasy obniżka
tzn. [T] = [(Inflacja, bez_zmian)] B
należy w kolejnej iteracji znaleźć dodatkowy
warunek który wyeliminuje przypadki 4, 5
Ze zbioru T(G) usuwamy warunek [(Inflacja,
bez_zmian)]
Zatem T(G) = {(Deficyt_budż, bez_zmian),
(Deficyt_budż, wzrost), (Rezerwy_dew, wzrost),
(Rezerwy_dew, bez_zmian)}
17. Algorytm LEM2
Zakładamy wstępnie żeB = G = {3, 6, 8} Algorytm
oraz π = Ø
LEM2
Zatem:
[(Deficyt_budż, bez_zmian)] = {1, 5, 8}
[(Defizyt_budż, wzrost)] = {2, 3, 4, 6, 7}
[(Rezerwy_dew, wzrost)] = {1, 3, 7, 8}
[(Rezerwy_dew, bez_zmian)] = {6}
Zatem T(G)
Spośród
wszystkich
tych
= {(Deficyt_budż,
2 par wybieramy
par wybieramy
bez_zmian),
te, które
te, które
mają mają
największą część
(Deficyt_budż,
mocwzrost),
tzn.
wspólną
pokrywają
(Rezerwy_budż,
ze zbiorem
najmniejszą
G:bez_zmian)}
liczbę
(Deficyt_budż,
przypadków
oraz
z innej
wzrost)
kategorii
oraz (Rezerwy_dew,
(obniżka), czyliwzrost)
pokrywają
wybieramy
T
= {(Inflacja,
po
(Rezerwy_dew,
bez_zmian),
2 przypadki (Rezerwy_budż,
wzrost).
wzrost)}
Więc [T] = {3, 8}
18.
Reguła 1:JEŻELI
Inflacja
JESTjest
spadek
Ponieważ
spełniony
warunek
TO
Stopy_proc
JEST obnizka
[T]
B można utworzyć
regułę R3
Reguła 2:
JEŻELI Rezerwy_dew JEST spadek
TO Stopy_proc JEST obnizka
Reguła 3:
JEŻELI Inflacja JEST bez_zmian
ORAZ Rezerwy_dew JEST wzrost
TO Stopy_proc JEST podwyżka
π = π {T} = Ø {3, 8} = {3, 8}
G = B – [T] = {3, 6, 8} – {3, 8} = {6}
19. Algorytm LEM2
Zatem:[(Deficyt_budż, bez_zmian)] = {1, 5, 8}
[(Defizyt_budż, wzrost)] = {2, 3, 4, 6, 7}
[(Rezerwy_dew, bez_zmian)] = {6}
Spośród
wszystkich
par wybieramy
te, które
Zatem T(G)
tych
= {(Deficyt_budż,
2 par wybieramy
bez_zmian),
tą, która
ma mają
największą
część
wspólną
ze najmniejszą
zbiorem G={6}:
(Deficyt_budż,
Moc
wzrost)}
tzn.
pokrywa
liczbę
(Deficyt_budż,
wzrost)
oraz (Rezerwy_dew,
przypadków z innej
kategorii
(obniżka), czyli
bez_zmian)
pokrywająbez_zmian)]
przypadek
6 B można
wybieramy
Oraz
[(Rezerwy_dew,
(Rezerwy_dew,
bez_zmian).
utworzyć regułę R4
20.
Reguła 1:JEŻELI Inflacja JEST spadek
TO Stopy_proc JEST obnizka
Reguła 2:
JEŻELI Rezerwy_dew JEST spadek
TO Stopy_proc JEST obnizka
Reguła 3:
JEŻELI Inflacja JEST bez_zmian
ORAZ Rezerwy_dew JEST wzrost
TO Stopy_proc JEST podwyżka
Reguła 4:
JEŻELI Rezerwy_dew JEST bez_zmian
TO Stopy_proc JEST podwyżka
21.
π = π {T} = Ø {6} = {3, 6, 8}G = B – [T] = {3, 6, 8} – {3, 6, 8} = Ø
G = Ø zatem wszystkie przypadki z kategorii
podwyżka zostały pokryte przez reguły
Algorytm kończy działanie
22. Zadanie praktyczne
Dla pliku OWOC_0X.tab przygotuj zbiórreguł za pomocą algorytmu LEM2.
(X – ostatnia cyfra z numeru indeksu studenta)
Sprawozdanie (BB)
Termin – 2 tygodnie po zajęciach
23. Literatura i materiały pomocnicze:
K:\ZSHippe\SISE\K:\MW\SISE\


















 informatics
informatics








