Similar presentations:
Architektura. Systemów Komputerowych (wykład 1)
1. Architektura Systemów Komputerowych wykład 1
2. ASK - prowadzący
dr inż. Artur Arciuche-mail: a.arciuch@vizja.net
tel. 22 6839401
wykład i laboratorium
mgr inż. Łukasz Laszko
laboratorium
ASK
2
3. Zaliczenie
można uzyskać 100 punktów50 punktów za ćwiczenia
laboratoryjne (25 zalicza)
50 punktów za egzamin (25 zalicza)
zaliczenie przedmiotu: uzyskać co
najmniej 50 punktów (łącznie i nie
mniej niż po 25 za każdy rygor)
ćwiczenia laboratoryjne: na zaliczenie
przedmiot: egzamin na ocenę
ASK
3
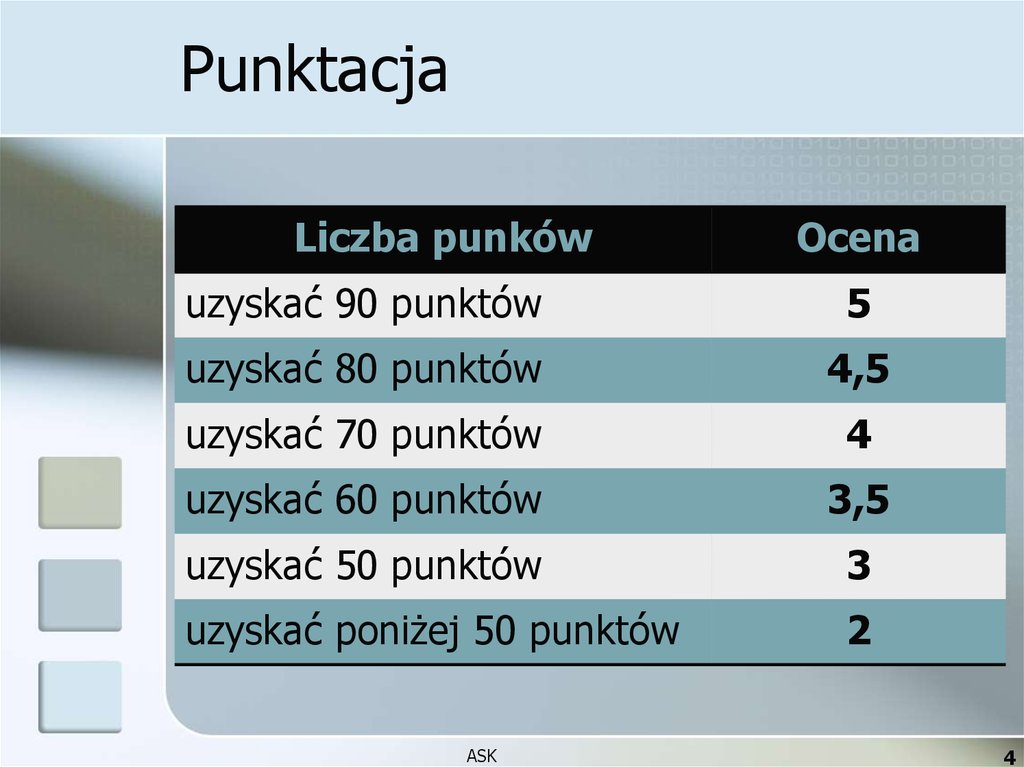
4. Punktacja
Liczba punkówOcena
uzyskać 90 punktów
5
uzyskać 80 punktów
4,5
uzyskać 70 punktów
4
uzyskać 60 punktów
3,5
uzyskać 50 punktów
3
uzyskać poniżej 50 punktów
2
ASK
4
5. Literatura
Stallings W.:Barczak A., Florek J., Sydoruk T.:
Elektroniczne techniki cyfrowe, Vizja
Press&IT Sp.z.o.o, Warszawa, 2006
Organizacja i architektura systemu
komputerowego, WNT, 2004
ASK
5
6. Nazwa przedmiotu
Pojęcia:architektura komputerów
organizacja komputerów
ASK
6
7. Systemy liczbowe
pozycyjne systemy liczbowesystemy wykorzystywane w naukach
komputerowych
kod dwójkowy
kod ósemkowy i szesnastkowy
kod BCD
kod ASCII
konwersje
ASK
7
8. System liczbowy
pozycyjnydwójkowy
dziesiętny
…
niepozycyjny
rzymski
…
ASK
8
9. Cechy systemu liczbowego pozycyjnego
LP ci ci 1...c1c0 ,gdzie:
• L – liczba w systemie liczbowym P
• P – podstawa systemu
• ck – cyfra na k-tej pozycji, ck ∊ {0,…,P-1}
• k – pozycja
value( LP )
I 1
c
P ,
j
j
gdzie I – liczba cyfr w liczbie
j 0
ASK
9
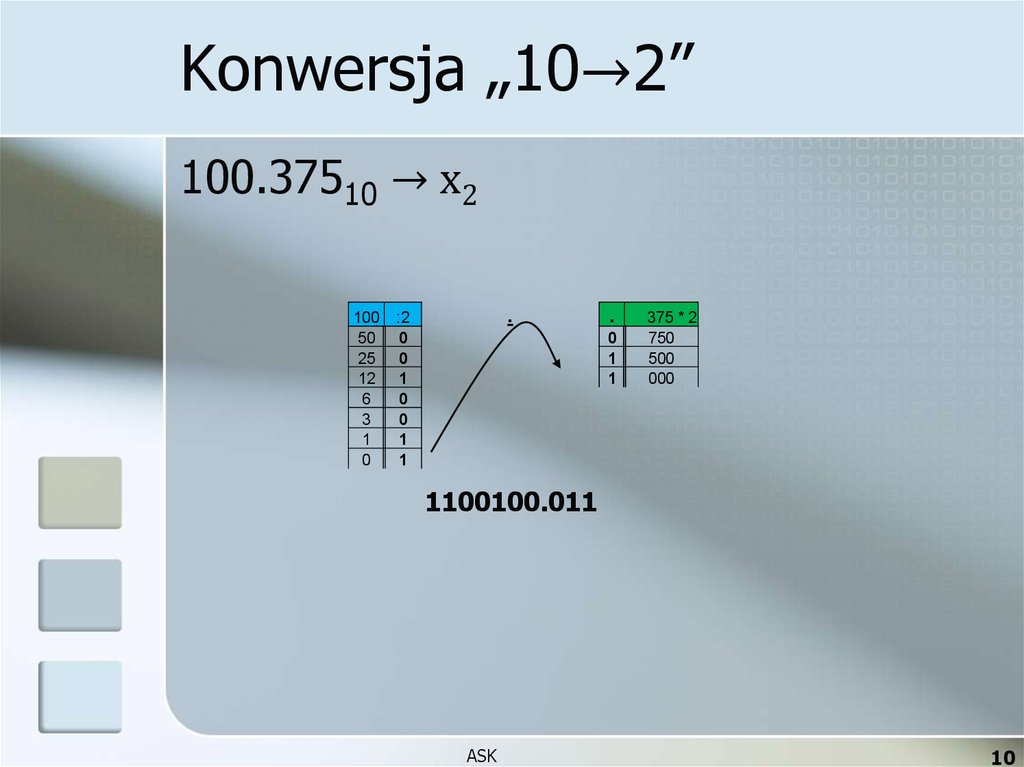
10. Konwersja „10→2”
100.37510 → x2100
50
25
12
6
3
1
0
.
:2
0
0
1
0
0
1
1
.
0
1
1
375 * 2
750
500
000
1100100.011
ASK
10
11. Konwersja „10→16”
200.62510 →x16200:16
C8
0C
.
0. 625 * 16
A 000
C8.A
konwersja „16 ↔ 2”,
C8.A
konwersja „2 ↔8”
11001000.1010
1100 1000 . 1010
ASK
310.5
11
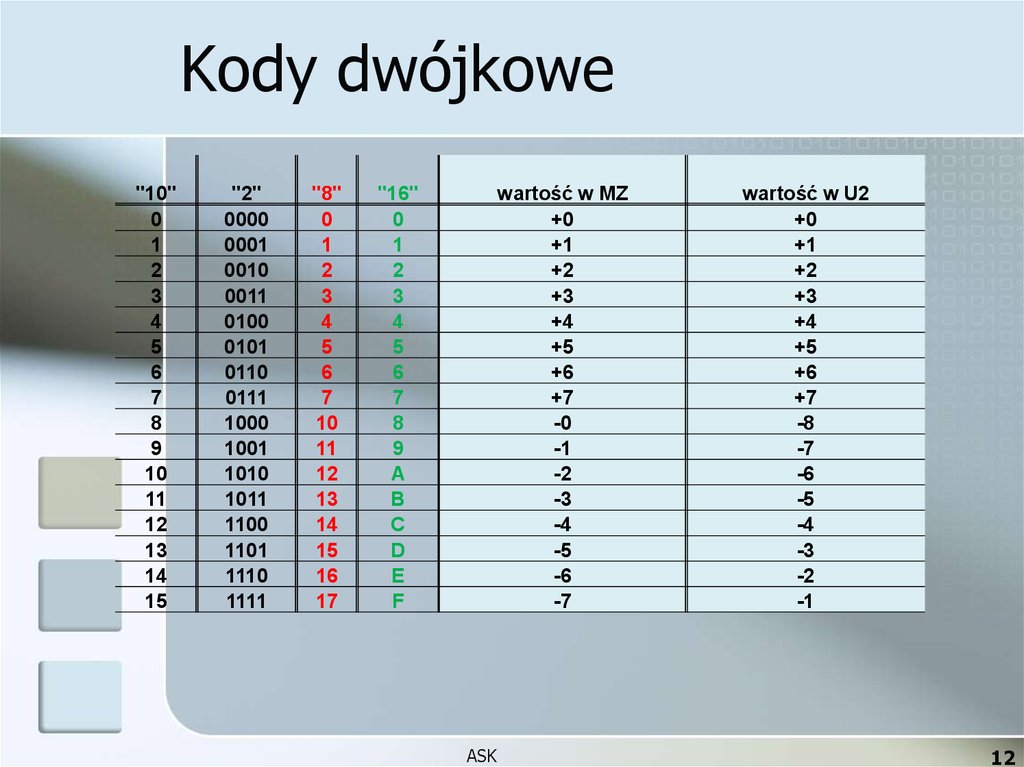
12. Kody dwójkowe
"10"0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
"2"
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
"8"
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
wartość w MZ
+0
+1
+2
+3
+4
+5
+6
+7
-0
-1
-2
-3
-4
-5
-6
-7
"16"
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
ASK
wartość w U2
+0
+1
+2
+3
+4
+5
+6
+7
-8
-7
-6
-5
-4
-3
-2
-1
12
13. Działania na liczbach dwójkowych w kodzie U2
Zamiana na liczbę przeciwną00010101
21
11101010
negacja
+
1
11101011
-21
Dodawanie
Odejmowanie
pożyczka
przeniesienia
111
00001110
+ 00011110
00101100
-
ASK
2
12
0011
0101
1110
13
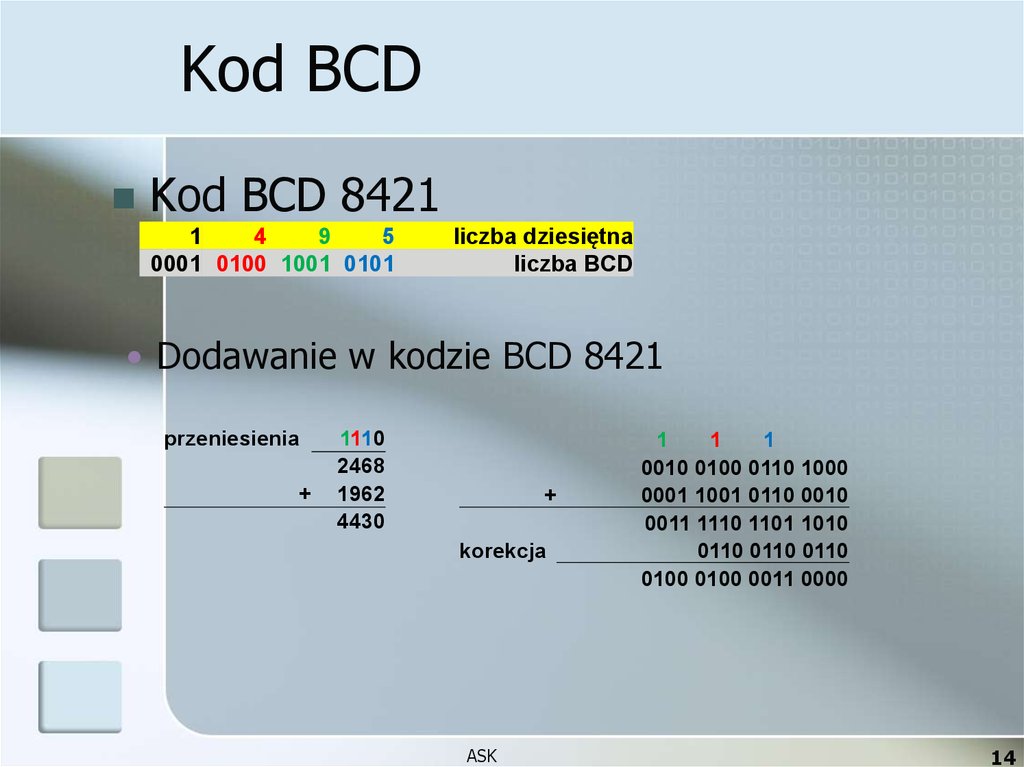
14. Kod BCD
Kod BCD 84211
4
9
5
0001 0100 1001 0101
liczba dziesiętna
liczba BCD
Dodawanie w kodzie BCD 8421
przeniesienia
+
1110
2468
1962
4430
+
korekcja
ASK
1
1
1
0010 0100 0110 1000
0001 1001 0110 0010
0011 1110 1101 1010
0110 0110 0110
0100 0100 0011 0000
14
15. Liczby zmiennoprzecinkowe
01
2
3
4
5
6
7
8
9
10
11
12
13
15
00 200 01 200 10 200 11 200
00 201 01 201 10 201 11 201
00 210
01 210 10 210 11 210
00 211
01 211 10 211 11 211
ASK
15
16. Format IEEE 754
ASK16
17. Zapis liczby w kodzie IEEE 754
liczbazmiennoprzecinkowa
z m P w : 4 10 2 , 010101 21010
znak = 0 - mantysa dodatnia ; znak = 1 - mantysa ujemna; normalizacja = 1.ułamek
podstawa = 2; wykładnik - 8-bitowy; przesunięcie wykładnika = 127
Zapisać liczbę 20 w postaci 32 bitowej liczby IEEE 754
2010 10100 2 10100 20 1.0100 24 1.0100 24 127 1.0100 2131
1.0100 210000011
1. - w domyśle
znak przesunięty wykładnik mantysa (ułamek)
0
10000011
010….0
0100000110100000000000000000000
ASK
17
18. Format IEEE 754
ASK18
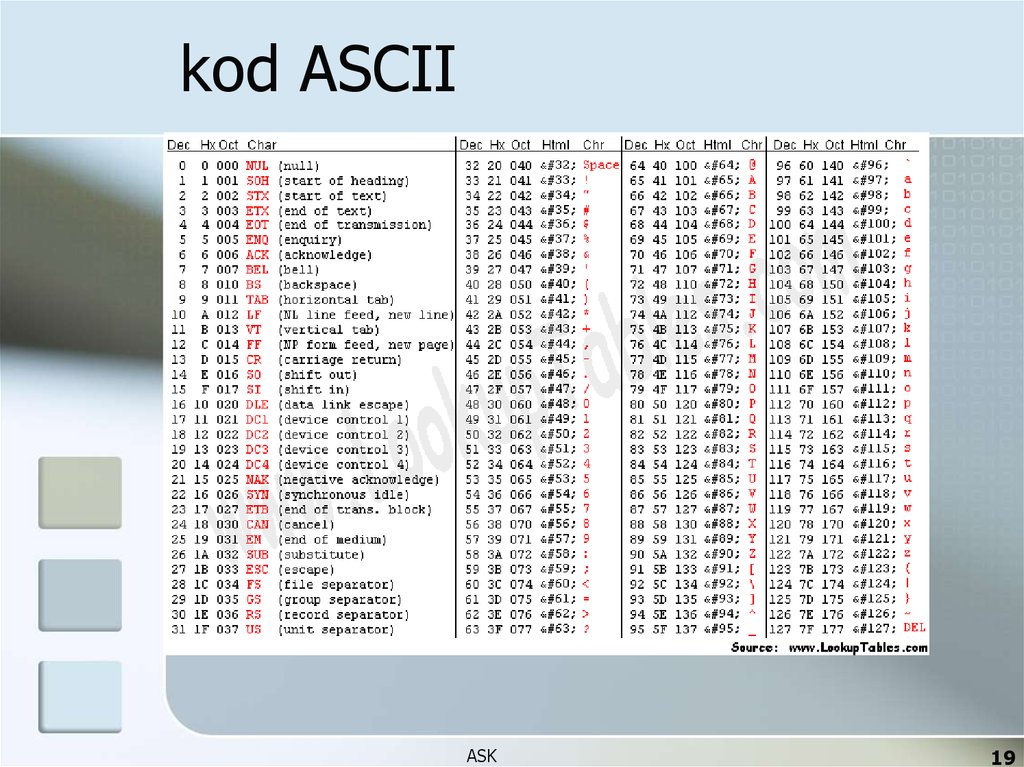
19. kod ASCII
ASK19
20. Zmienne logiczne
fałsz (false), 0prawda (true), 1
ASK
20
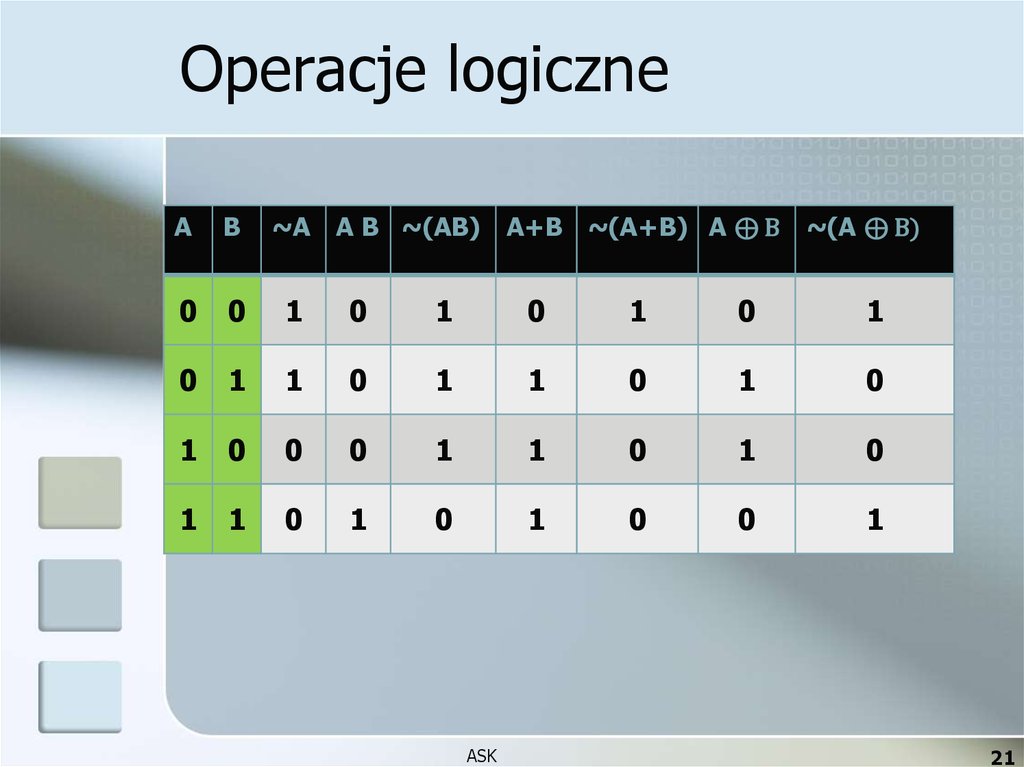
21. Operacje logiczne
A B ~(AB) A+B ~(A+B) A ⊕ B ~(A ⊕ B)A
B
~A
0
0
1
0
1
0
1
0
1
0
1
1
0
1
1
0
1
0
1
0
0
0
1
1
0
1
0
1
1
0
1
0
1
0
0
1
ASK
21
22. Podsumowanie
system liczbowysystemy liczbowe w naukach
komputerowych
zmienne i operacje logiczne
ASK
22
















 informatics
informatics








