Similar presentations:
Algorytmy sortujące
1. Materiały pochodzą z Platformy Edukacyjnej Portalu www.szkolnictwo.pl
Wszelkie treści i zasoby edukacyjne publikowane na łamach Portalu www.szkolnictwo.pl mogą być wykorzystywane przez jego Użytkowników wyłączniew zakresie własnego użytku osobistego oraz do użytku w szkołach podczas zajęć dydaktycznych. Kopiowanie, wprowadzanie zmian, przesyłanie, publiczne odtwarzanie
i wszelkie wykorzystywanie tych treści do celów komercyjnych jest niedozwolone. Plik można dowolnie modernizować na potrzeby własne oraz do wykorzystania
w szkołach podczas zajęć dydaktycznych.
2. algorytmy sortujące
Sortowanie przez wstawianieSortowanie przez wybór
3. Wstęp
Sortowanie–
jeden
z
podstawowych
problemów
informatyki. Polega na uporządkowaniu zbioru danych
względem pewnych cech charakterystycznych każdego
elementu tego zbioru. Szczególnym przypadkiem jest
sortowanie względem wartości każdego elementu, np.
sortowanie liczb, słów itp.
Algorytmy sortowania są stosowane w celu uporządkowania
danych, umożliwieniu stosowania wydajniejszych algorytmów
(np. wyszukiwania) i prezentacji danych w sposób czytelniejszy
dla człowieka.
Jeśli jest konieczne posortowanie zbioru większego niż
wielkość dostępnej pamięci, stosuje się algorytmy sortowania
zewnętrznego.
4. Slajd 4
Zbiór posortowany to taki zbiór, w którym kolejne elementy sąpoukładane w pewnym porządku (kolejności). Porządek ten możemy
określić za pomocą relacji ≥ lub ≤ (albo dowolnej innej relacji
porządkowej, która jednoznacznie wyznacza kolejność elementów w
zbiorze). Równość jest konieczna w przypadku, gdy elementy zbioru
mogą przyjmować takie same wartości. Na przykład zbiór liczb:
Z = { 1, 4, 4, 5, 6, 8, 8, 9 }
jest posortowany rosnąco, ponieważ pomiędzy każdymi dwoma
kolejnymi elementami zachodzi relacja, w której element poprzedni
jest mniejszy lub równy od elementu następnego
Odwrotnie, zbiór:
Z = { 9, 8, 7, 6, 4, 4, 2, 1, 0 }
jest posortowany malejąco, ponieważ pomiędzy każdymi dwoma
kolejnymi elementami zachodzi relacja, w której element poprzedni
jest większy lub równy od elementu następnego.
W przypadku, kiedy zbiór nie składa się z liczb, należy określić dla
każdego elementu tzw. klucz (ang. key), wedłóg którego dokonywane
jest sortowanie.
Klucz jest liczbą, dlatego obowiązują dla niego podane wcześniej
zasady kolejności elementów.
5. Czasowa złożoność obliczeniowa
(ang. computational complexity)algorytmu sortującego (istnieje również złożoność pamięciowa) –
określa statystycznie czas wykonywania algorytmu w zależności od
liczby danych wejściowych.
Czasowa złożoność obliczeniowa wyrażana jest liczbą tzw.
operacji dominujących, czyli takich, które mają bezpośredni wpływ
na czas wykonywania algorytmu. Dzięki takiemu podejściu
uniezależnia się czasową złożoność obliczeniową od szybkości
komputera, na którym dany algorytm jest realizowany.
Złożoność obliczeniowa charakteryzowana jest przy pomocy tzw.
notacji O (omikron). Zapis O( ) określamy mianem klasy złożoności
obliczeniowej algorytmu.
Klasa
czasowej
złożoności
obliczeniowej
umożliwia
porównywanie wydajności różnych algorytmów sortujących. Z
reguły proste algorytmy posiadają wysoką złożoność obliczeniową długo dochodzą do wyniku końcowego.
Algorytmy bardziej skomplikowane posiadają mniejszą złożoność
obliczeniową - szybko dochodzą do rozwiązania.
6. Slajd 6
W poniższej tabeli przedstawiono przykładowezłożoności obliczeniowej algorytmów.
zapisy
klas
O(n)
Algorytm o liniowej zależności czasu wykonania od ilości
danych. Dwukrotny wzrost liczby przetwarzanych danych
powoduje dwukrotny wzrost czasu wykonania. Tego typu
złożoność powstaje, gdy dla każdego elementu należy
wykonać stałą liczbę operacji.
O(n2)
Algorytm, w którym czas wykonania rośnie z kwadratem
liczby przetwarzanych elementów. Dwukrotny wzrost liczby
danych powoduje czterokrotny wzrost czasu wykonania. Tego
typu złożoność powstaje, gdy dla każdego elementu należy
wykonać ilość operacji proporcjonalną do liczby wszystkich
elementów.
O(n log n)
Dobre algorytmy sortujące mają taką właśnie złożoność
obliczeniową. Czas wykonania przyrasta dużo wolniej od
wzrostu kwadratowego. Tego typu złożoność powstaje, gdy
zadanie dla n elementów można rozłożyć na dwa zadania
zawierające po połowie elementów.
O(n!)
Bardzo pesymistyczne algorytmy, czas wykonania rośnie
szybko wraz ze wzrostem liczby elementów wejściowych,
czyli znalezienie rozwiązania może zająć najszybszym
komputerom całe wieki lub tysiąclecia. Takich algorytmów
O(an)
7. Pamięciowa złożoność obliczeniowa
Oprócz złożoności czasowej definiuje się równieżzłożoność pamięciową. Określa ona ilość zasobów
komputera, których wymaga dany algorytm w zależności
od liczby danych wejściowych. Tutaj także ma
zastosowanie notacja omikron. Podczas określania
złożoności algorytmu należy wziąć pod uwagę oba typy
złożoności obliczeniowej.
Ze względu na złożoność pamięciową algorytmy sortujące dzielimy na dwie
podstawowe grupy:
Algorytmy
sortujące w miejscu (ang. in place) - wymagają stałej liczby
dodatkowych struktur danych, która nie zależy od liczby elementów sortowanego
zbioru danych (ani od ich wartości). Dodatkowa złożoność pamięciowa jest klasy
O(1). Sortowanie odbywa się wewnątrz zbioru. Ma to bardzo istotne znaczenie w
przypadku dużych zbiorów danych, ponieważ mogłoby się okazać, iż posortowanie
ich nie jest możliwe z uwagi na brak pamięci w systemie. Sortowanie w miejscu,
jest bardzo dużą zaletą.
Algorytmy
nie sortujące w miejscu - wymagają zarezerwowania w pamięci
dodatkowych obszarów, których wielkość jest uzależniona od liczby sortowanych
elementów lub od ich wartości. Tego typu algorytmy są zwykle bardzo szybkie w
działaniu, jednakże wymagają dodatkowej pamięci. Dlatego może się okazać, iż taki
algorytm nie będzie w stanie posortować dużego zbioru danych, ponieważ system
komputerowy nie posiada wystarczającej ilości pamięci RAM.
8. Slajd 8
Algorytmy sortujące dzieli się również na dwie grupy:Algorytmy
stabilne - zachowują kolejność elementów
równych. Oznacza to, iż elementy o tych samych wartościach będą
występowały w tej samej kolejności w zbiorze posortowanym, co w
zbiorze nieposortowanym. Czasami ma to znaczenie, gdy sortujemy
rekordy bazy danych i nie chcemy, aby rekordy o tym samym kluczu
zmieniały względem siebie położenie.
sortowanie bąbelkowe (ang. bubblesort) – O(n2)
sortowanie przez wstawianie (ang. insertion sort) – O(n2)
sortowanie przez scalanie (ang. merge sort) – O(nlogn), wymaga
O(n) dodatkowej pamięci
sortowanie przez zliczanie (ang. counting sort lub count sort) –
O(n + k), wymaga O(n + k) dodatkowej pamięci
sortowanie kubełkowe (ang. bucket sort) – O(n), wymaga O(k)
dodatkowej pamięci
sortowanie pozycyjne (ang. radix sort) – O(d(n + k)), gdzie k to
wielkość domeny cyfr, a d szerokość kluczy w cyfrach. Wymaga
O(n + k) dodatkowej pamięci
sortowanie biblioteczne (ang. library sort) – O(nlogn),
pesymistyczny O(n2)
9. Slajd 9
Algorytmyniestabilne - kolejność wynikowa elementów
równych jest nieokreślona (zwykle nie zostaje zachowana).
sortowanie przez wybór (ang. selection sort) O(n2) – może
być stabilne po odpowiednich zmianach
sortowanie Shella – (ang. shellsort) złożoność nieznana
sortowanie grzebieniowe – (ang. combsort) złożoność nieznana
sortowanie szybkie – (ang. quicksort) Θ(nlogn), pesymistyczny
O(n2); z wykorzystaniem algorytmu selekcji "mediana median"
("magicznych piątek") do wyszukiwania mediany,
pesymistyczna złożoność to O(nlogn)
sortowanie introspektywne – (ang. introspective sort lub
introsort) O(nlogn)
sortowanie przez kopcowanie – (ang. heapsort) O(nlogn)
10. Sortowanie przez wybór - Selection Sort
Jest to jedna z prostszych metod sortowania posiadająca klasęczasowej złożoności obliczeniowej równą O(n2).
Polega na wyszukaniu elementu mającego się znaleźć na zadanej
pozycji i zamianie miejscami z tym, który jest tam obecnie. Operacja
jest wykonywana dla wszystkich indeksów sortowanej tablicy.
Algorytm przedstawia się następująco:
wyszukaj
minimalną wartość z tablicy spośród elementów
od i+1 do końca tablicy
zamień
wartość minimalną, z elementem na pierwszej
pozycji (i)
Gdy zamiast wartości minimalnej wybierana będzie maksymalna,
wówczas tablica będzie posortowana od największego do
najmniejszego elementu.
Algorytm jest niestabilny. Sortowanie odbywa się w miejscu.
11. Przykład
Posortujmy dany zbiór (5 8 2 9 4). Kolorem niebieskimktóre zostały już posortowane.
Zbiór
oznaczone zostały elementy zbioru,
Opis operacji
5
8
2
9
4
Wyszukujemy najmniejszy element w zbiorze. Jest nim
liczba 2.
2
8
5
9
4
Znaleziony element minimalny wymieniamy z pierwszym
elementem zbioru - liczbą 5
2
8
5
9
4
Wśród pozostałych elementów wyszukujemy element
najmniejszy. Jest nim liczba 4.
2
4
5
9
8
Znaleziony element minimalny wymieniamy z drugim
elementem zbioru - liczbą 8.
2
4
5
9
8
Znajdujemy kolejny element minimalny - liczbę 5.
2
4
5
9
8
Wymieniamy go z samym sobą - element ten nie zmienia
zatem swojej pozycji w zbiorze.
2
4
5
9
8
Znajdujemy kolejny element minimalny
2
4
5
8
9
Wymieniamy go z liczbą 9
2
4
5
8
9
Ostatni element jest zawsze na właściwej pozycji.
Sortowanie zakończone
12. Specyfikacja problemu
Dane wejściowen - liczba elementów w sortowanym zbiorze, n N d[ ] - zbiór
n-elementowy, który będzie sortowany. Elementy zbioru mają
indeksy od 1 do n.
Dane wyjściowe
d[ ] - posortowany zbiór n-elementowy. Elementy zbioru mają
indeksy od 1 do n.
Zmienne pomocnicze
i, j - zmienne sterujące pętli, i, j N pmin - pozycja elementu
minimalnego w zbiorze d[ ], pmin N
Lista kroków
K01:
K02:
K03:
K04:
K05:
Dla j = 1, 2, ..., n - 1: wykonuj K02...K04
pmin ← j
Dla i = j + 1, j + 2, ..., n: jeśli d[i] < d[pmin], to pmin ← i
d[j] ↔ d[pmin]
Zakończ
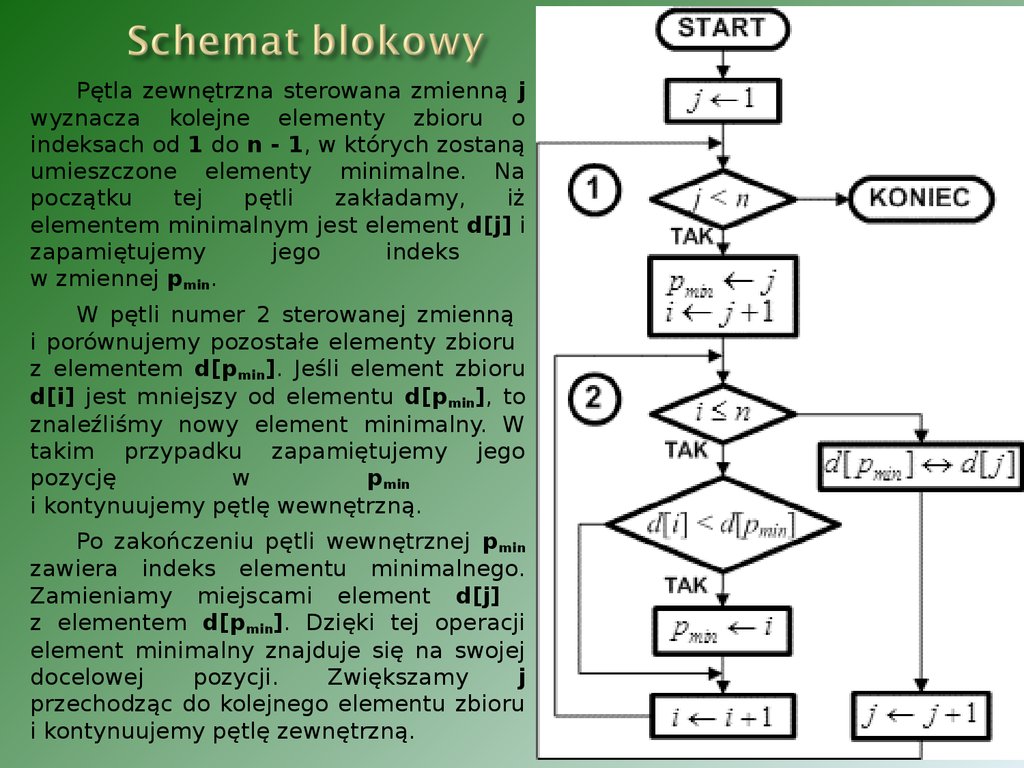
13. Schemat blokowy
Pętla zewnętrzna sterowana zmienną jwyznacza kolejne elementy zbioru o
indeksach od 1 do n - 1, w których zostaną
umieszczone elementy minimalne. Na
początku
tej
pętli
zakładamy,
iż
elementem minimalnym jest element d[j] i
zapamiętujemy
jego
indeks
w zmiennej pmin.
W pętli numer 2 sterowanej zmienną
i porównujemy pozostałe elementy zbioru
z elementem d[pmin]. Jeśli element zbioru
d[i] jest mniejszy od elementu d[pmin], to
znaleźliśmy nowy element minimalny. W
takim przypadku zapamiętujemy jego
pozycję
w
pmin
i kontynuujemy pętlę wewnętrzną.
Po zakończeniu pętli wewnętrznej pmin
zawiera indeks elementu minimalnego.
Zamieniamy miejscami element d[j]
z elementem d[pmin]. Dzięki tej operacji
element minimalny znajduje się na swojej
docelowej
pozycji.
Zwiększamy
j
przechodząc do kolejnego elementu zbioru
i kontynuujemy pętlę zewnętrzną.
14. Sortowanie przez wstawianie - Insertion Sort
Jest to prosty algorytm sortowania, o złożoności O(n2),sortowanie odbywa się w miejscu . Mimo że jest znacznie mniej
wydajny od algorytmów takich jak quicksort czy heapsort posiada
pewne zalety:
wydajny
dla danych wstępnie posortowanych
wydajny
dla zbiorów o niewielkiej liczebności
stabilny
Algorytm polega na usuwaniu pewnego elementu z danych
wejściowych
i wstawianiu go na odpowiednie miejsce w wynikach. Wybór
następnego elementu z danych jest dowolny.
15. Schemat działania algorytmu:
Najważniejszą operacją w opisywanym algorytmie sortowaniajest
wstawianie
wybranego
elementu
na
listę
uporządkowaną. Zasady są następujące:
Na
początku sortowania lista uporządkowana zawiera tylko
jeden, ostatni element zbioru. Jednoelementowa lista jest zawsze
uporządkowana.
Ze
zbioru zawsze wybieramy element leżący tuż przed listą
uporządkowaną. Element ten zapamiętujemy w zewnętrznej
zmiennej. Miejsce, które zajmował, możemy potraktować jak puste.
Wybrany
element porównujemy z kolejnymi elementami listy
uporządkowanej.
Jeśli
natrafimy na koniec listy, element wybrany wstawiamy na
puste miejsce - lista rozrasta się o nowy element.
Jeśli
element listy jest większy od wybranego, to element
wybrany wstawiamy na puste miejsce - lista rozrasta się o nowy
element.
Jeśli
element listy nie jest większy od wybranego, to element
listy przesuwamy na puste miejsce. Dzięki tej operacji puste miejsce
wędruje
na
liście
przed
kolejny
element.
Kontynuujemy
porównywanie, aż wystąpi sytuacja z punktu 4 lub 5.
16. Przykład
Dla przykładu wstawmy według opisanej metody pierwszy element zbioru listęuporządkowaną utworzoną z pozostałych elementów [7 3 4 5 8]. Elementy listy uporządkowanej
zaznaczyliśmy kolorem niebieskim. Puste miejsce zaznaczyliśmy kolorem żółtym:
Zbiór
7
3
Opis operacji
4
5
8
Element 7 znajduje się tuż przed listą uporządkowaną.
8
Wybieramy ze zbioru element 7. Zajmowane przez niego miejsce
staje się puste.
8
Porównujemy 8 z pierwszym elementem listy uporządkowanej, z
liczbą 4.
8
Ponieważ element 3 jest mniejszy od elementu wybranego 7,
przesuwamy go na puste miejsce. Puste miejsce wędruje w
kierunku końca listy uporządkowanej.
8
3
4
5
7
3
4
5
7
3
<
<
4
5
7
4
4
5
8
Porównujemy 7 z kolejnym elementem listy uporządkowanej, z
liczbą 4.
17. Slajd 17
Ciąg dalszy przykładu:Zbiór
Opis operacji
7
3
4
<
<
5
8
7
3
4
5
8
4 jest mniejsze od 7, zatem wędruje na puste miejsce, które
przesuwa się przed kolejny element listy uporządkowanej, liczbę
5.
Porównujemy 7 z 5.
7
3
4
5
<
<
8
7
4
3
5
4
6
5
7
5 jest mniejsze od 7, wędruje na puste miejsce.
8
Porównujemy 7 z kolejnym elementem listy uporządkowanej, z
liczbą 9.
8
Element wybrany wędruje na puste miejsce, ponieważ jest
mniejszy od liczby 8 listy uporządkowanej. Operacja wstawiania
jest zakończona. Lista rozrasta się o jeden element.
18. Specyfikacja problemu
Dane wejściowen - liczba elementów w sortowanym zbiorze, n Î N d[ ] - zbiór nelementowy, który będzie sortowany. Elementy zbioru mają indeksy od 1
do n.
Dane wyjściowe
d[ ] - posortowany zbiór n-elementowy. Elementy zbioru mają indeksy
od 1 do n.
Zmienne pomocnicze
i, j - zmienne sterujące pętli, i, j Î N x - zawiera wybrany ze zbioru
element.
Lista kroków
K01: Dla j = n - 1, n - 2, ..., 1: wykonuj K02...K04
K02:
x ← d[j]; i ← j + 1
K03:
Dopóki ( i ≤ n ) ∧ ( x > d[i] ): wykonuj d[i - 1] ← d[i]; i ← i +
1
K04: d[i - 1] ← x
K05: Zakończ
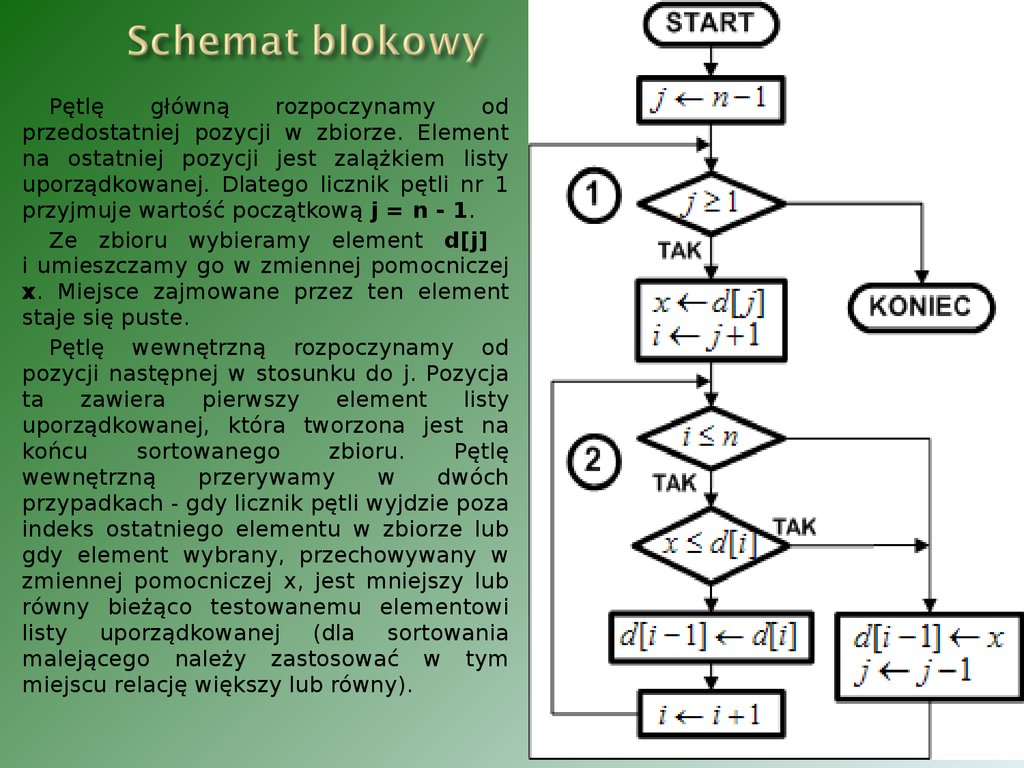
19. Schemat blokowy
Pętlęgłówną
rozpoczynamy
od
przedostatniej pozycji w zbiorze. Element
na ostatniej pozycji jest zalążkiem listy
uporządkowanej. Dlatego licznik pętli nr 1
przyjmuje wartość początkową j = n - 1.
Ze zbioru wybieramy element d[j]
i umieszczamy go w zmiennej pomocniczej
x. Miejsce zajmowane przez ten element
staje się puste.
Pętlę wewnętrzną rozpoczynamy od
pozycji następnej w stosunku do j. Pozycja
ta
zawiera
pierwszy
element
listy
uporządkowanej, która tworzona jest na
końcu
sortowanego
zbioru.
Pętlę
wewnętrzną
przerywamy
w
dwóch
przypadkach - gdy licznik pętli wyjdzie poza
indeks ostatniego elementu w zbiorze lub
gdy element wybrany, przechowywany w
zmiennej pomocniczej x, jest mniejszy lub
równy bieżąco testowanemu elementowi
listy uporządkowanej (dla sortowania
malejącego należy zastosować w tym
miejscu relację większy lub równy).
20. Schemat blokowy c.d.
W obu przypadkach na puste miejscema trafić zawartość zmiennej x i pętla
zewnętrzna jest kontynuowana. Zauważ,
iż pozycja tego miejsca w zbiorze jest
równa i - 1.
Jeśli żaden z warunków przerwania
pętli wewnętrznej nr 2 nie wystąpi, to
przesuwamy bieżący element listy na
puste miejsce i kontynuujemy pętlę
wewnętrzną.
Podsumowując: pętla zewnętrzna
wybiera ze zbioru kolejne elementy o
indeksach od n - 1 do 1, pętla
wewnętrzna
szuka
dla
wybranych
elementów miejsca wstawienia na liście
uporządkowanej, po znalezieniu którego
pętla zewnętrzna wstawia wybrany
element na listę. Gdy pętla zewnętrzna
przebiegnie
wszystkie
elementy
o
indeksach od n - 1 do 1, zbiór będzie
posortowany.
21. Podsumowanie
W prezentacji przedstawiono dwa rodzaje algorytmów: algorytmstabilny – na przykładzie sortowania przez wstawianie i
algorytm niestabilny - na przykładzie sortowania przez wybór.
Algorytm sortowania przez wstawianie nie uwzględnia faktu posortowania
zbioru. Jednakże również nie wyróżnia on przypadku posortowania zbioru w
kierunku odwrotnym. Dla tego algorytmu złożoność czasowa nie zależy od
rozkładu elementów w sortowanym zbiorze.
Przy sortowaniu przez wybór algorytm wykorzystuje fakt posortowania zbioru.
Dla zbiorów w znacznym stopniu uporządkowanych klasa czasowej złożoności
obliczeniowej algorytmu jest prawie liniowa. Czas sortowania takich zbiorów jest
bardzo krótki.
Najbardziej niekorzystnym przypadkiem jest sortowanie zbioru posortowanego
odwrotnie - czas sortowania jest najdłuższy. Czas sortowania zbioru o losowym
rozkładzie elementów jest o połowę krótszy.
Algorytm sortowania przez wybór jest dużo lepszy od sortowania przez
wstawianie w przypadku zbiorów w znacznym stopniu uporządkowanych.
Również zbiory o losowym rozkładzie elementów będą posortowane szybciej.
Jedynie w przypadku pesymistycznym, gdy zbiór jest posortowany odwrotnie,
algorytm jest wolniejszy od algorytmu sortowania przez wybór. Te cechy czynią
algorytm sortowania przez wstawianie zalecanym, prostym algorytmem
sortującym klasy O(n2).
22. Bibliografia
• S. J. Russell, P. Norvig (2003). Artificial Intelligence: A ModernApproach. Second Edition, Prentice Hall.
• Von Neumann, J: Zur Theorie der Gesellschaftsspiele Math. Annalen.
100 (1928)
• John L Casti: Five golden rules: great theories of 20th-century
mathematics – and why they matter. New York: Wiley-Interscience,
1996
• Donald E. Knuth: Sztuka programowania. T. 1. Warszawa:
Wydawnictwo Naukowo-Techniczne, 2002
• Neil Gershenfeld i Isaac L. Chuang, Molekularne komputery
kwantowe; Świat Nauki, sierpień 1998
• Nadrian C. Seeman, Na granicy życia i nanotechnologii; Świat Nauki,
lipiec 2004
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford
Stein: Wprowadzenie do algorytmów;WNT, wyd. VI 2004
• pl.wikipedia.org/
• algorytm.org/
• neuralnets.eu/
• wazniak.mimuw.edu.pl/index.php?title=Sztuczna_inteligencja
• computerchess.us/gtchess




















 informatics
informatics








