Атомдық физика

1.

“Атомдық физика”

2. Жоспар

Резерфорд тәжірибесі
Бор теориясы
Сутегі атомы
Сутегі атомының спектрлық сериялары
Толқындық функция
Шредингер теңдеуін сутек атомына қолдану
Атомның механикалық және магниттік
моменттері
Паули ережесі

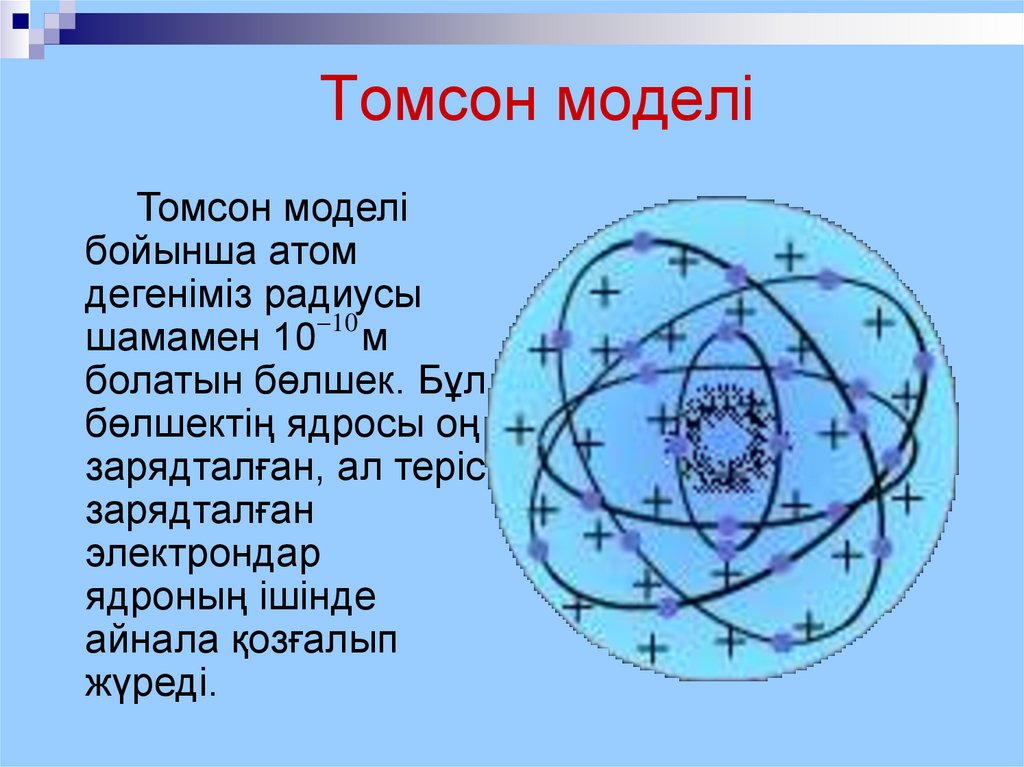
3. Томсон моделi

Томсон моделi
бойынша атом
дегенiмiз радиусы
шамамен 10 10 м
болатын бөлшек. Бұл
бөлшектің ядросы оң
зарядталған, ал терiс
зарядталған
электрондар
ядроның iшiнде
айнала қозғалып
жүредi.

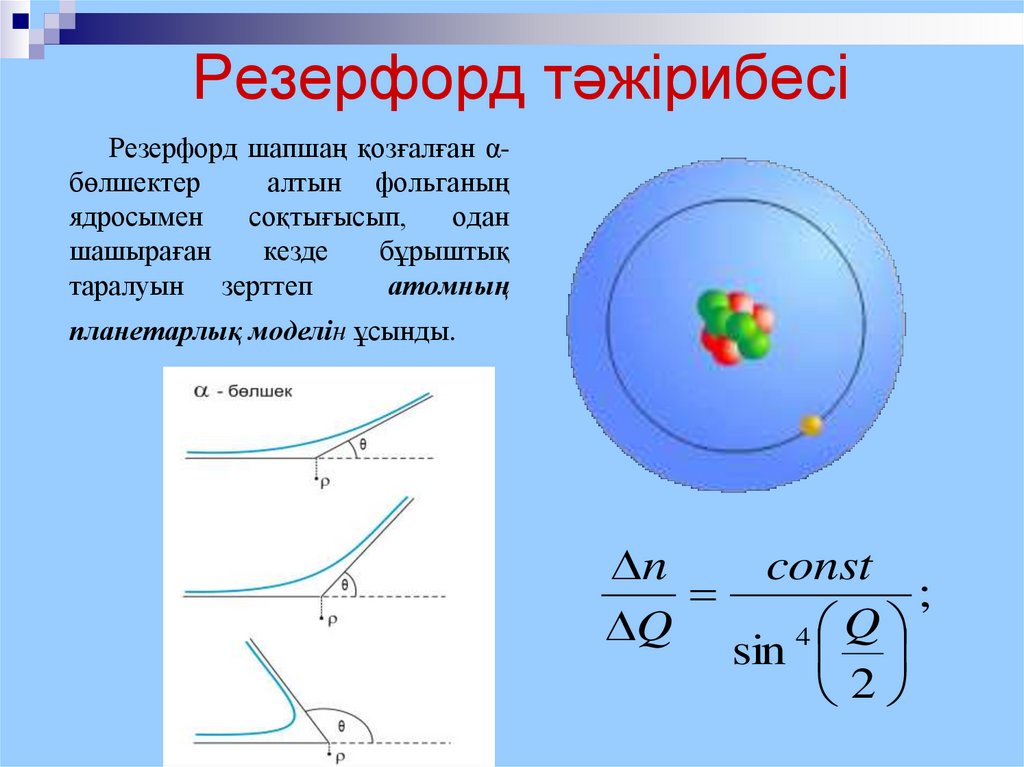
4. Резерфорд тәжiрибесi

5. Резерфорд тәжiрибесi

Резерфорд шапшаң қозғалған αбөлшектер
алтын фольганың
ядросымен
соқтығысып,
одан
шашыраған
кезде
бұрыштық
таралуын зерттеп
атомның
планетарлық моделiн ұсынды.
n
Q
const
;
4 Q
sin
2

6. Бор постулаттары

Атомдар, тек стационарлық күйлерде бола алады.
2. Сәуле
шығару немесе жұту атомның тек бiр
стационарлық күйден екiншi стационарлық күйге өткен
кезде ғана болады.
1.
h En Em ;
Мұндағы En және E m осы стационар күйлердiң
энергиясы, ал h – Планк тұрақтысы.
3. Импульс моменті квантталады
m r nh;
h
;
2
(n= 1, 2, 3 …)

7. Сутегі атомы

m r nh;
Электронның атомдағы
импульс моменті
e2
F
;
2
4 0 r
(1)
Кулон күші
m 2
Fц .т.
;
r
(2)
Центрге тартқыш күш
1
(1) Мен (2) теңестіреміз
m 2
1 e2
;
2
r
4 0 r

8.

4 0 h n
rn
;
2
me
2
2
Стационарлық
орбиталардың
радиусы
0
r1 0,56 A
Стационарлық
күйлердің энергиясы
2
1 m e4
En
;
2 2
4 0 2 h n
E1 13,6э.в.
Қалыпты күйдегі
энергия

9.

h En Em ;
(1)
me4 1
1
En Em
2h n 2 m 2
(2)
me4 1
1
2
3
2
2h m
n
me 4
R
2h 3
(4)
me 4 1
1
2
3
2
4 h m
n
(3)
R = 3,29 1016 c-1 Ридберг тұрақтысы
(5)
1
1
R 2 2
m n
(6)

10.

Сутегі атомының спектрлық сериялары
R
1
1
2
n2
1
-
Лайман сериясы
R
-
Бальмер сериясы
1
1
2
2
n
2
1
1
R 2 2
n
3
- Пашен сериясы
1
1
R 2 2
n
4
- Брэкет сериясы
1
1
2
2
n
5
- Пфунд сериясы
R

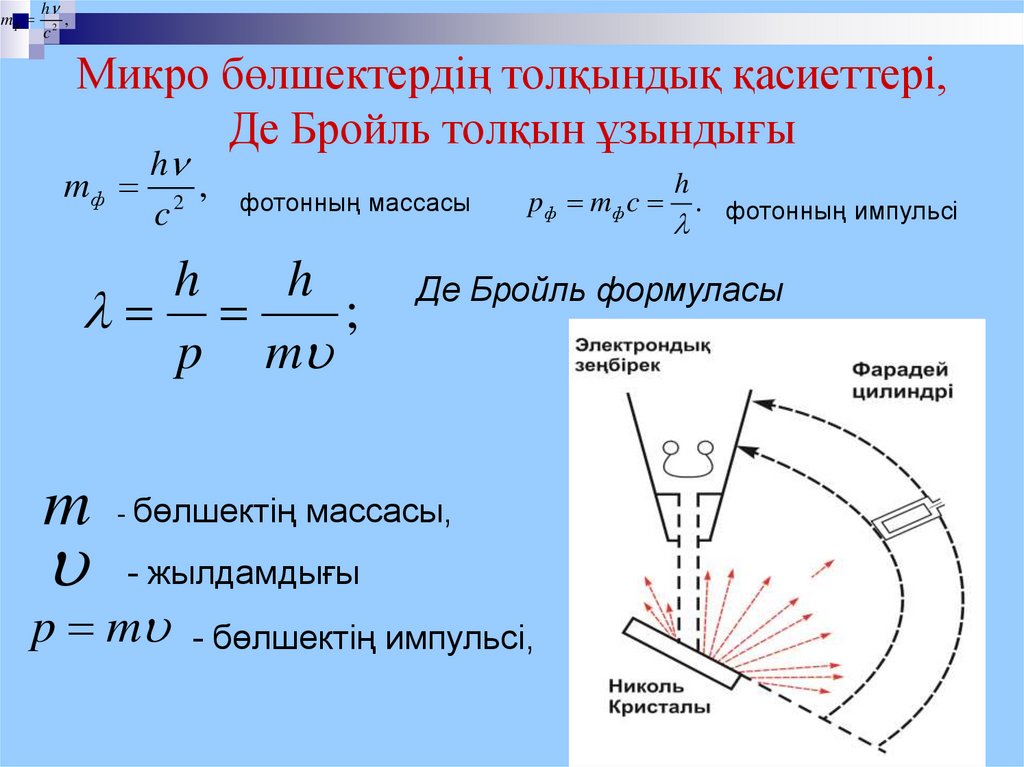
11. Микро бөлшектердің толқындық қасиеттері, Де Бройль толқын ұзындығы

mф
h
,
c2
Микро бөлшектердің толқындық қасиеттері,
Де Бройль толқын ұзындығы
h
mф 2 ,
c
фотонның массасы
h
h
;
p m
p ф mф c
. фотонның импульсі
Де Бройль формуласы
m бөлшектің массасы,
-
- жылдамдығы
h
p m - бөлшектің импульсі,

12.

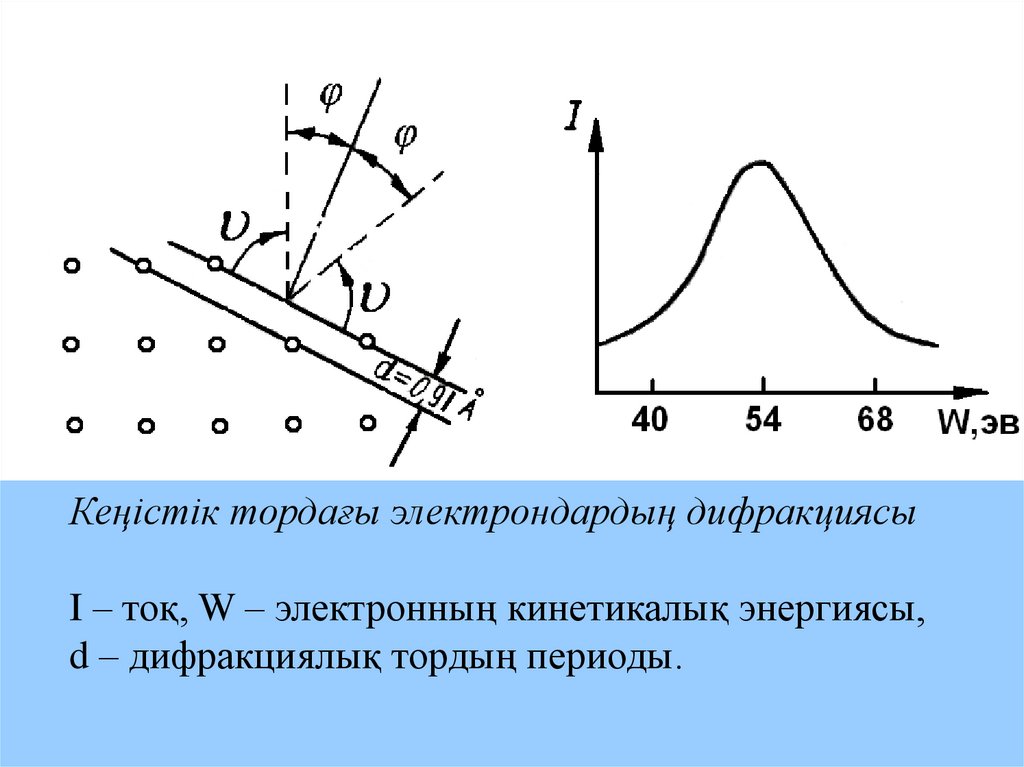
Кеңістік тордағы электрондардың дифракциясы
I – тоқ, W – электронның кинетикалық энергиясы,
d – дифракциялық тордың периоды.

13. Корпускулды – толқындық дуализм.

Луи де Бройль бөлшектер қозғалысы кезінде
төңірегіне толқын шығаратындығын дәлелдеді,
оны де Бройль толқындары деп атайды.
Энергиясы Е және импульсі Р - ға тең
қозғалыстағы еркін бөлшекті жазық толқынмен
байланыстырады:
r , t Ae
i t k r
r - радиус-векторы, t-уақыт, А-толқын амплитудасы.

14.

Толқынның жиілігі және толқындық векторы
бөлшектің энергиясы және импульсімен байланысты:
Е ;
Р к;
Р
2
2
h
;
h
h
;
Р m

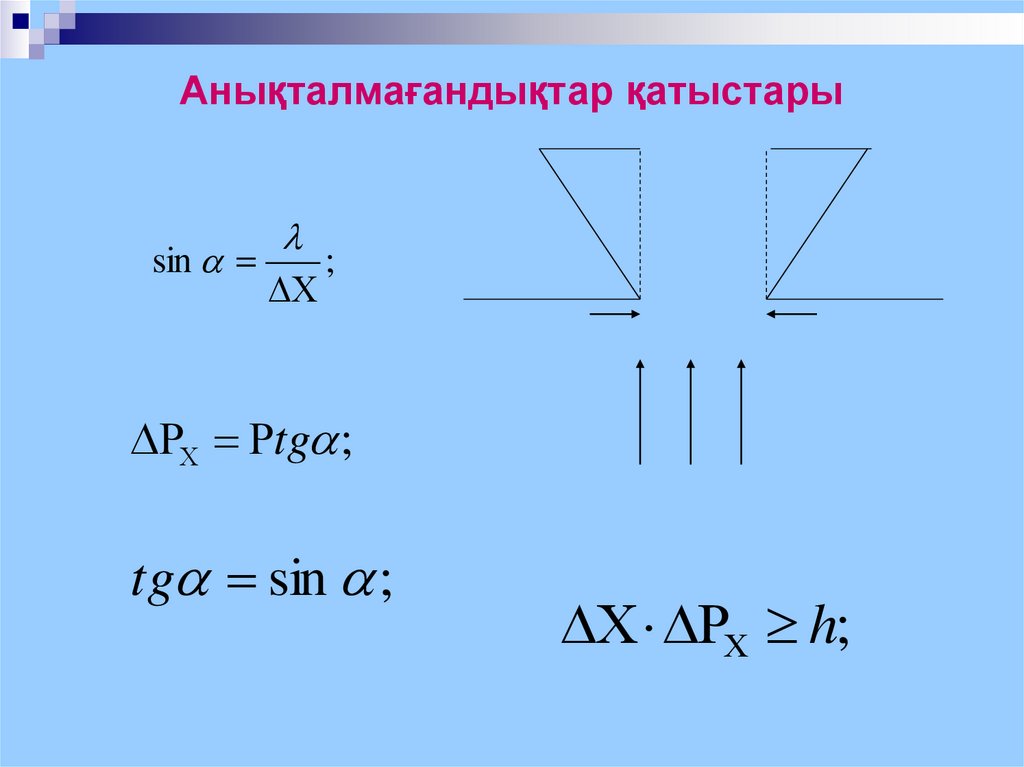
15. Анықталмағандықтар қатыстары

sin
;
tg ;
tg sin ;
h;

16. Гейзенбергтің анықталмағандық қатынасы

;
;

17. Толқындық функция

Ықтималдық теориясы бойынша dv көлемдегі
бөлшекті табу ықтималдылығы мынаған тең:
dW x, y, z, t dV x, y, z , t dV ;
2
dW
2
x, y , z , t
x, y, z, t x, y, z, t * x, y, z, t ;
dV
бұл ықтималдық тығыздығы деп аталынады.
W V , t dW dV x. y.z , t dV ;
2
v
v
v
Бұл өрнек ақиқат оқиғаның ықтималдығы.
x, y, z, t dV 1;
2
v

18.

Микрообъектіні сипаттайтын физикалық шамалар
бірге өлшенетін жиынтыққа біріктіріледі.
Әрбір толық жиынтық төрт тәуелсіз шамадан
тұрады:
x, y, z, ms
Px , Py , Pz , ms
E , l , m, ms
n, s, l , m – спиндік, орбиталық және магниттік
кванттық сандар.
Координаттар мен импульстер әр түрлі жиынтыққа
кіреді, сондықтан оларды бірге өлшеуге болмайды.

19. Шредингер теңдеуі

Импульсі P және энергиясы Е еркін бөлшектің қозғалысын
толқындық функциямен сипаттауға болады:
i
r , t A exp Pr Et ;
h
Мұндағы А – толқын амплитудасы.
Еркін бөлшектер үшін мына қатынас орындалады:
;
2m
2

20.

i / t
,
t
,
2
2
2
x
2
y
2
2
z
Сонда іздестіріп отырған теңдеуімізді табамыз
2
r , t
2
i
r , t ;
t
2m

21.

Бұл теңдеуді U r сыртқы өрісте қозғалатын бөлшектер
үшін жазуға болады
r , t ˆ
i
r , t ,
2
2
Hˆ
U r ;
2m
толық
энергия
операторы.
немесе
Гамильтон