Окружность, описанная около треугольника

1.

2.

Окружность называется
описанной около
треугольника, если она
проходит через все его
вершины.
В этом случае треугольник
называется вписанным в
окружность.

3.

А
О
В
С

4.

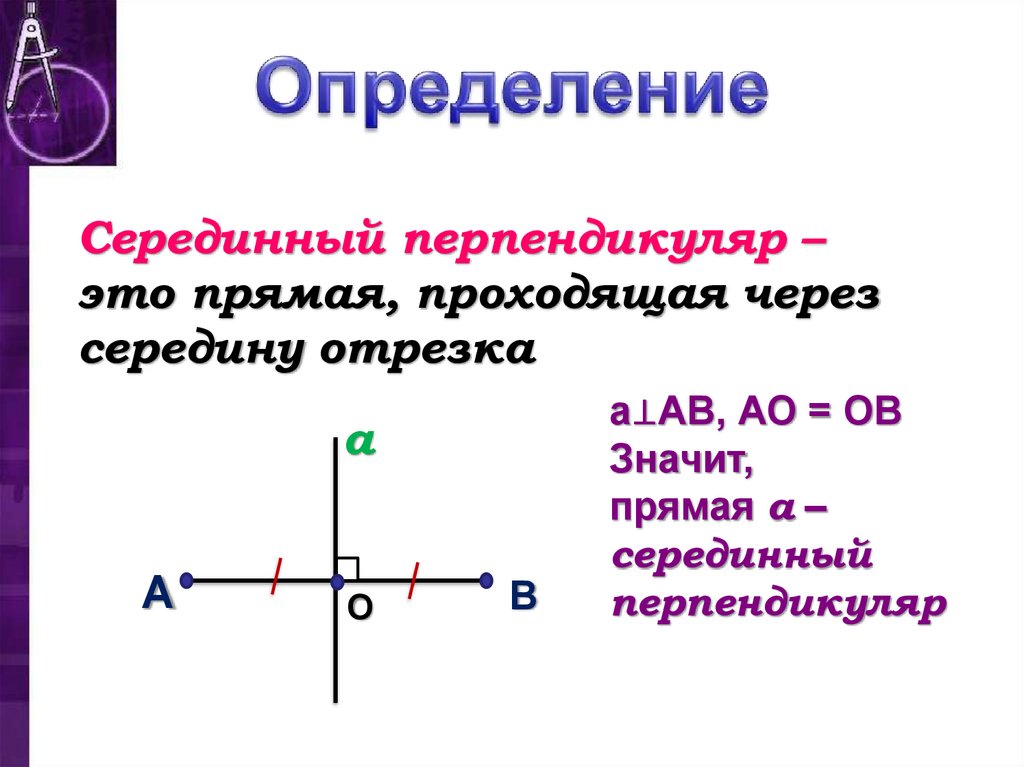
Серединный перпендикуляр –
это прямая, проходящая через
середину отрезка
а
А
О
В
а⊥АВ, АО = ОВ
Значит,
прямая а –
серединный
перпендикуляр

5.

Центр окружности,
описанной около
треугольника, является
точкой пересечения
серединных
перпендикуляров к
сторонам треугольника

6.

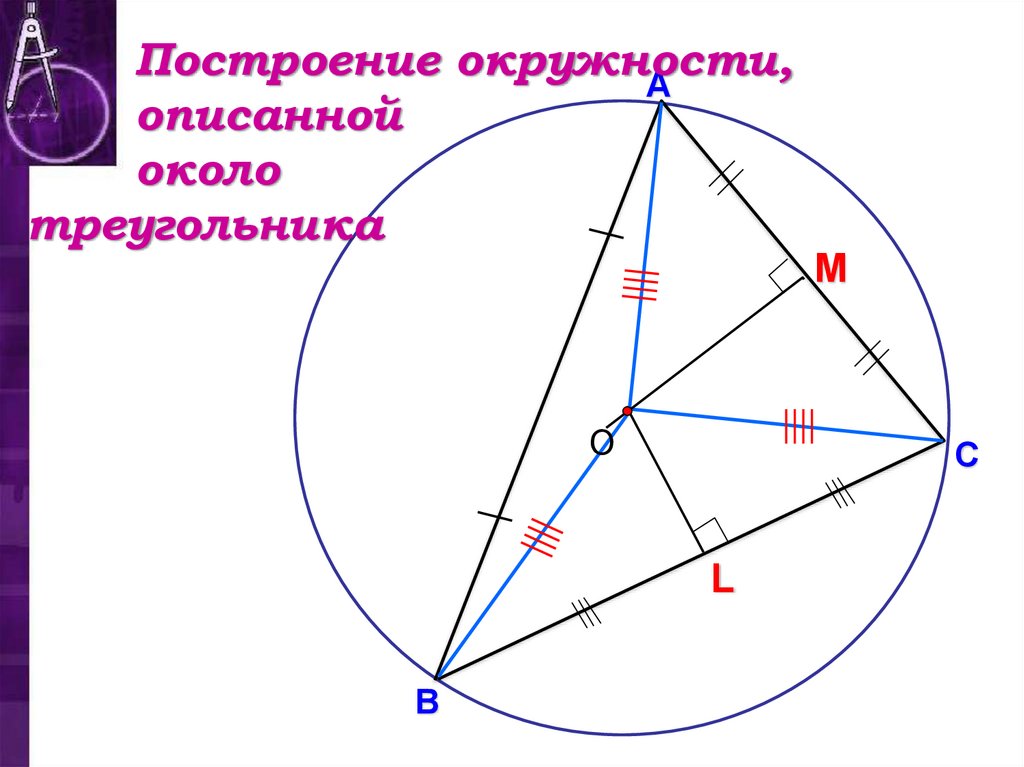
Построение окружности,
А
описанной
около
треугольника
M
K
О
С
L
В

7.

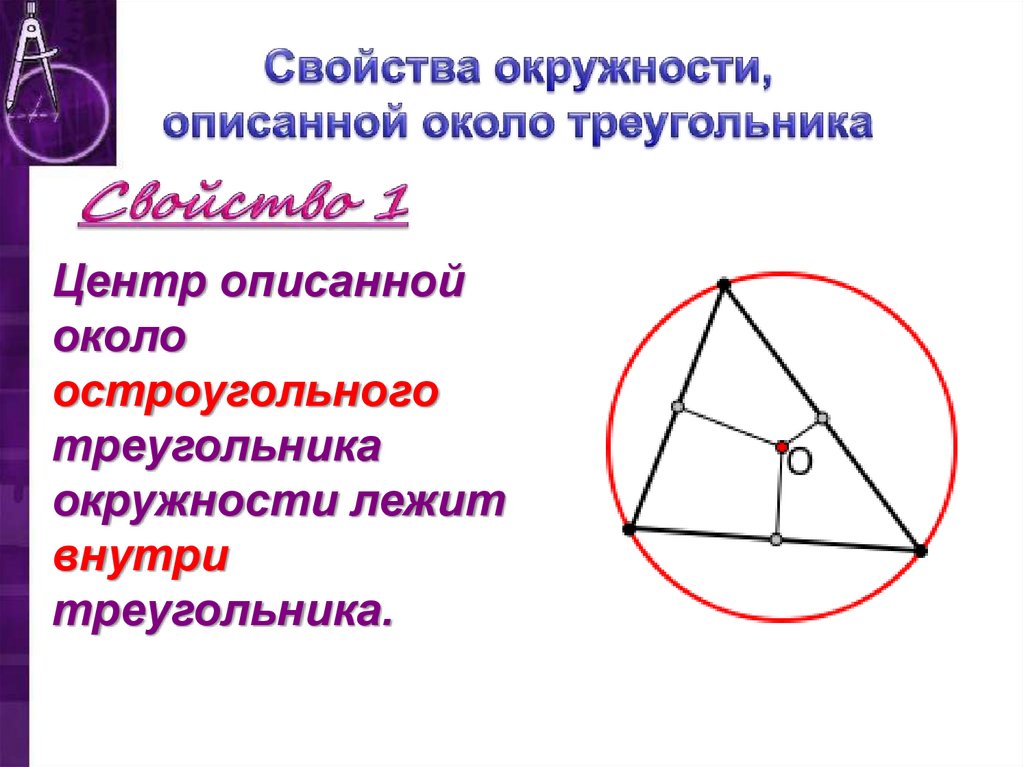
Центр описанной
около
остроугольного
треугольника
окружности лежит
внутри
треугольника.

8.

Центром
описанной около
прямоугольного
треугольника
окружности
является середина
гипотенузы.

9.

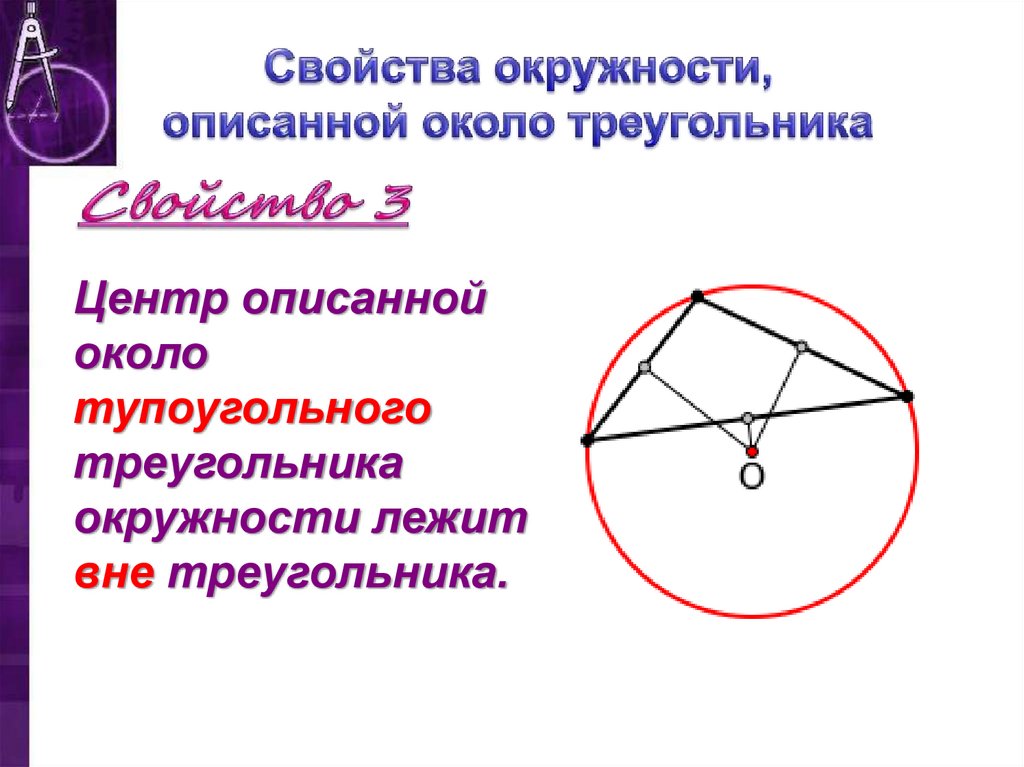
Центр описанной
около
тупоугольного
треугольника
окружности лежит
вне треугольника.

10.

1) Диаметр окружности, описанной
около прямоугольного треугольника,
равен 18 см. Найти длину медианы,
проведенной из вершины прямого угла
этого треугольника.

11.

С
А
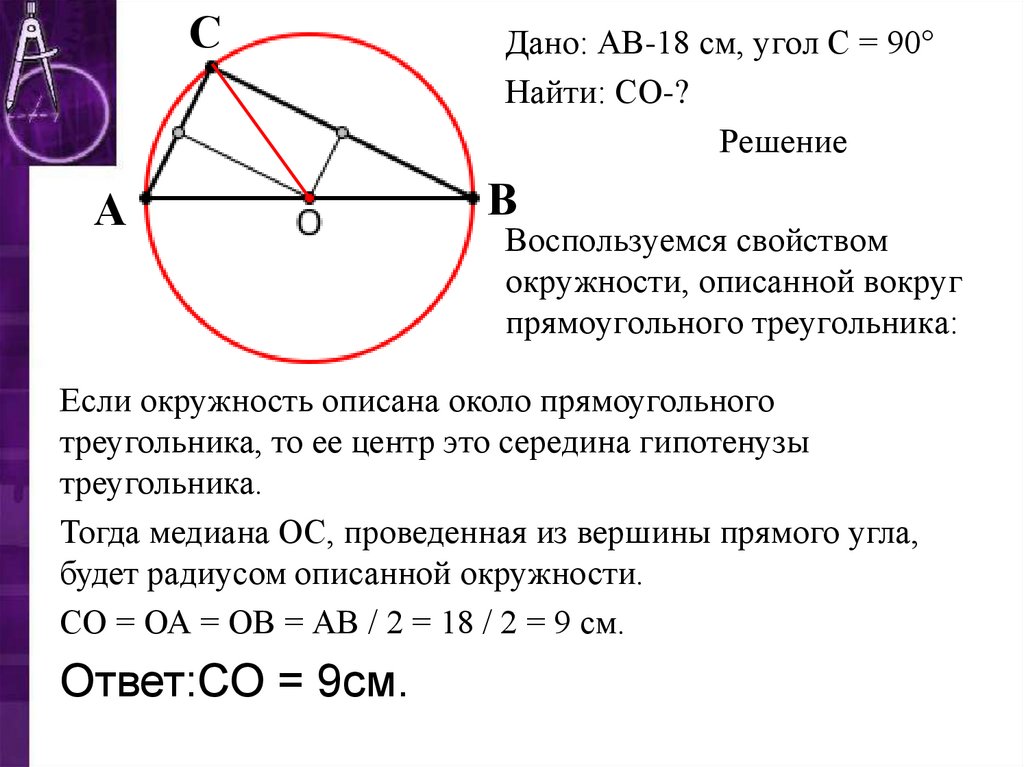
Дано: АВ-18 см, угол С = 90°
Найти: СО-?
Решение
В
Воспользуемся свойством
окружности, описанной вокруг
прямоугольного треугольника:
Если окружность описана около прямоугольного
треугольника, то ее центр это середина гипотенузы
треугольника.
Тогда медиана ОС, проведенная из вершины прямого угла,
будет радиусом описанной окружности.
СО = ОА = ОВ = АВ / 2 = 18 / 2 = 9 см.
Ответ:СО = 9см.

12.

2) Расстояние от центра О
до хорды АВ равно 15 см,
∠ ОАВ = 45º. Точка С
принадлежит хорде АВ,
причем АС=4ВС.
Найти длину отрезка АС.
3) В окружности с центром
О проведены радиусы ОА, ОВ и
ОС так, что ОВ ⊥ АС и
отрезки ОВ и АС
пересекаются. Докажите,
что АВ = ВС.

13.

Выполнить задачу №2 и
задачу №3