Similar presentations:
Программные продукты в математическом моделировании. Численные методы решения нелинейных уравнений
1.
Программные продукты вматематическом
моделировании.
Численные методы решения
нелинейных уравнений
2.
Постановка задачиПусть дано уравнение
f(x) = 0,
где функция f(x) определена и непрерывна
на некотором интервале a < x < b.
Всякое значение v, обращающее функцию f(x)
в нуль, т.е. такое, что f(v)=0, называется
корнем уравнения или нулем функции f(x).
3.
Методы решения нелинейных уравненийделятся на прямые и итерационные.
Прямые методы позволяют записать корни в
виде конечного соотношения (формулы).
Однако, только для простейших уравнений
удаётся найти решение в аналитическом виде,
т.е. записать формулу, выражающую искомую
величину x в явном виде через параметры
уравнения.
4.
случаев уравненияприходится решать,
используя
итерационные методы
В большинстве
Итерационный процесс состоит в последовательном
уточнении начального приближения
искомой
величины x. Каждый такой шаг называется
итерацией. В результате итераций находится
последовательность приближенных значений корня:
x1, x2, x3,……., xn.
Если эти значения с ростом n приближаются к
истинному значению корня, то говорят, что
итерационный процесс сходится.
5.
ПредположениеПредполагается, что уравнение f(x) = 0 имеет
лишь изолированные корни, т.е. для каждого
корня уравнения существует окрестность, не
содержащая других корней этого уравнения.
6.
Этапы решения задачи:1. Отделение корней, т.е. установление
возможных промежутков (интервалов), в
которых содержится один и только один
корень уравнения.
2. Уточнение приближенных корней, т.е.
доведение их до заданной степени
точности.
7.
Теорема 1.Если непрерывная функция
f(x) принимает значения
разных знаков на концах
отрезка [α ,β], т.е.
f(α)*f(β)<0, то внутри этого
отрезка содержится по
меньшей мере один корень
уравнения f(x)=0, т.е.
найдется хотя бы одно число ε
такое, что f(ε)=0.
8.
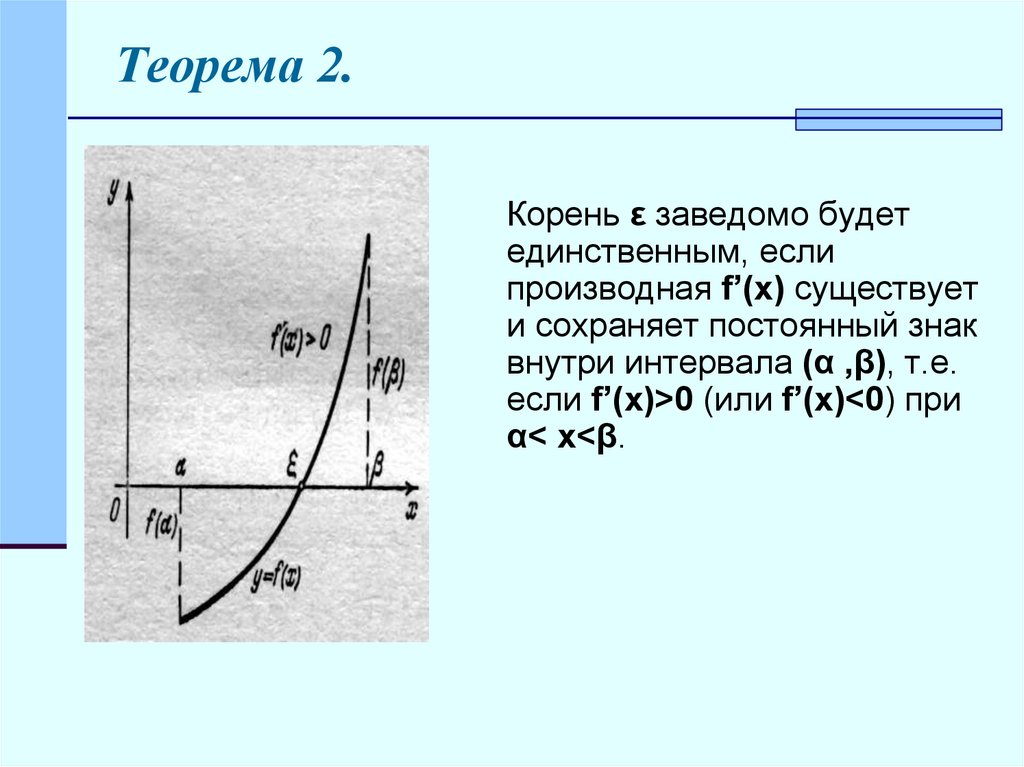
Теорема 2.Корень ε заведомо будет
единственным, если
производная f’(x) существует
и сохраняет постоянный знак
внутри интервала (α ,β), т.е.
если f’(x)>0 (или f’(x)<0) при
α< x<β.
9.
Методы отделения корнейграфический способ
определение знаков функции в ряде
промежуточных точек, выбор которых
учитывает особенности функции
специальные способа анализа функции
10.
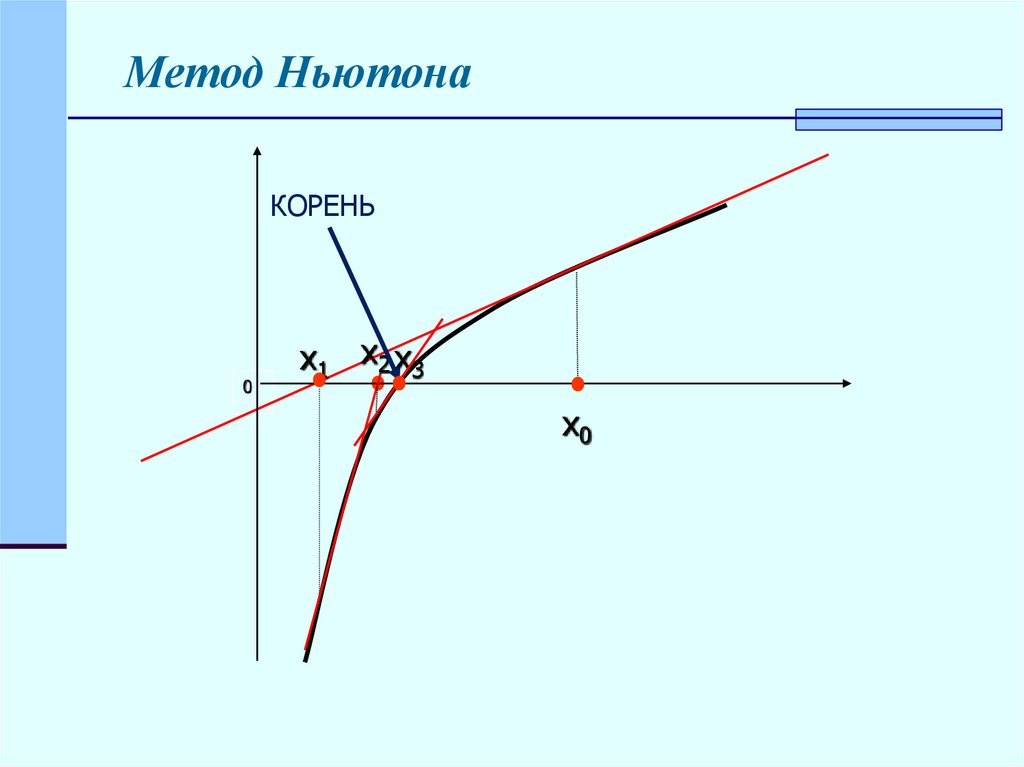
Методы приближенногонахождения (уточнения) корней
Метод половинного деления
(дихотомии)
Метод хорд
Метод касательных
Метод итераций
11.
ПримерНайти корни уравнения
3
x – 6x + 2 = 0
12.
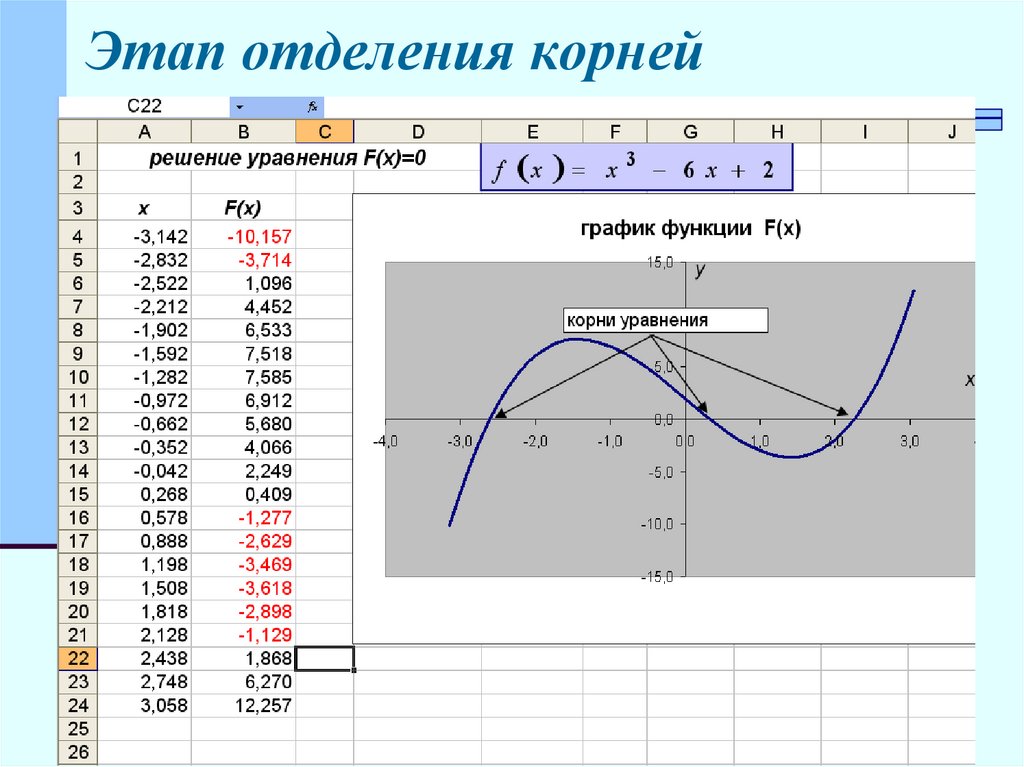
Этап отделения корней13.
Начальные приближения длянахождения корней
приблизительно -2,5 на интервале [-3,-2]
приблизительно 0,5 в интервале [0,1]
приблизительно 2,5 на интервале [2,3]
14.
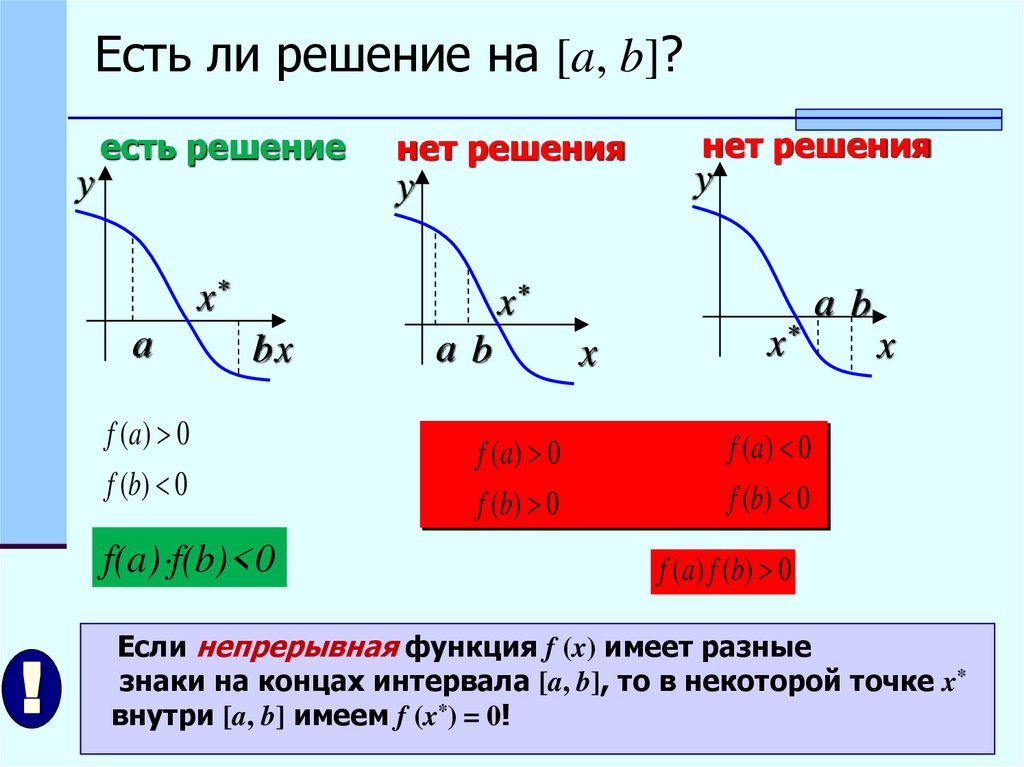
Есть ли решение на [a, b]?есть решение
y
нет решения
y
x*
a
y
x*
bx
f (a) 0
f (b) 0
f(a) f(b)<0
!
нет решения
ab
f (a) 0
f (b) 0
a b
x
x*
x
f (a) 0
f (b) 0
f (a) f (b) 0
Если непрерывная функция f (x) имеет разные
знаки на концах интервала [a, b], то в некоторой точке x*
внутри [a, b] имеем f (x*) = 0!
15.
Метод половинного деления (дихотомии)Условие наличия корня f(a)*f(b) < 0.
Вычисляется середина отрезка x = (a+b)/2.
Если f(x) = 0, то х - корень уравнения.
В противном случае выбирается тот из
отрезков [a, x] или [x, b], на концах которого
функция f(x) имеет разные знаки.
Вычисления завершаются при условии
|b – a| < ε, где ε – точность (малое число).
16.
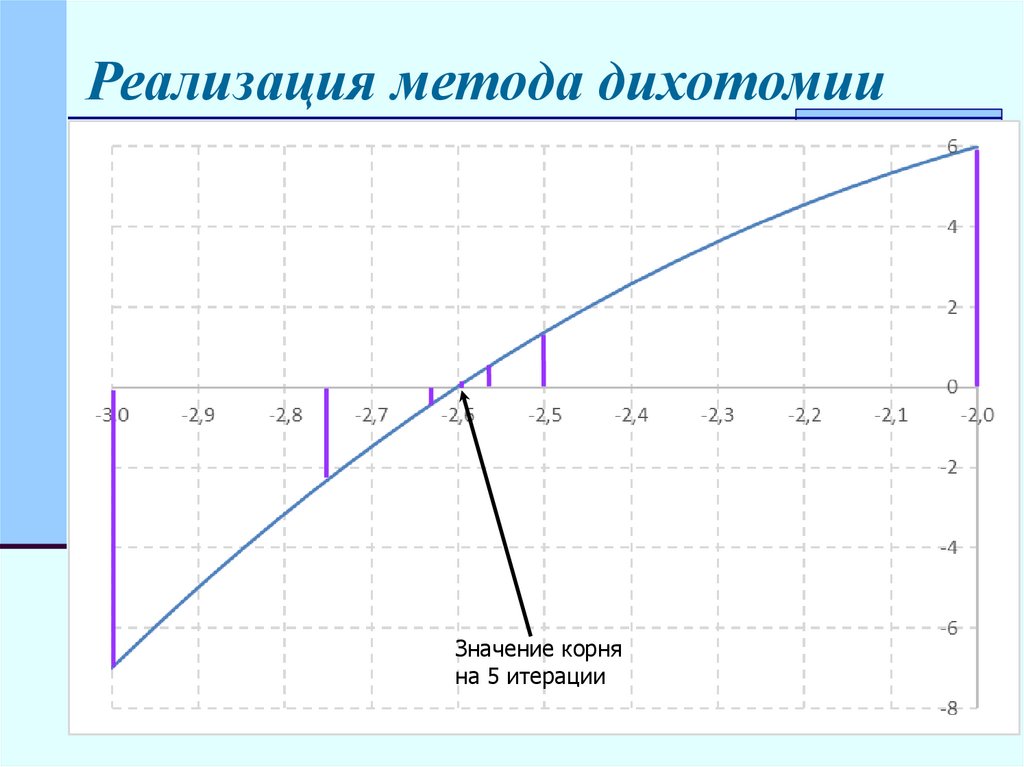
Пример применения метода дихотомиидля нахождения корня уравнения
f(x)= x3 – 6*x + 2 = 0
на интервале [-3,-2].
границы интервала: a = -3; b = -2;
значения функции на границах
интервала:
f(a) = -7; f(b) = 6
Точность вычисления: ε = 0.01
17.
Реализация метода дихотомииЗначение корня
на 5 итерации
18.
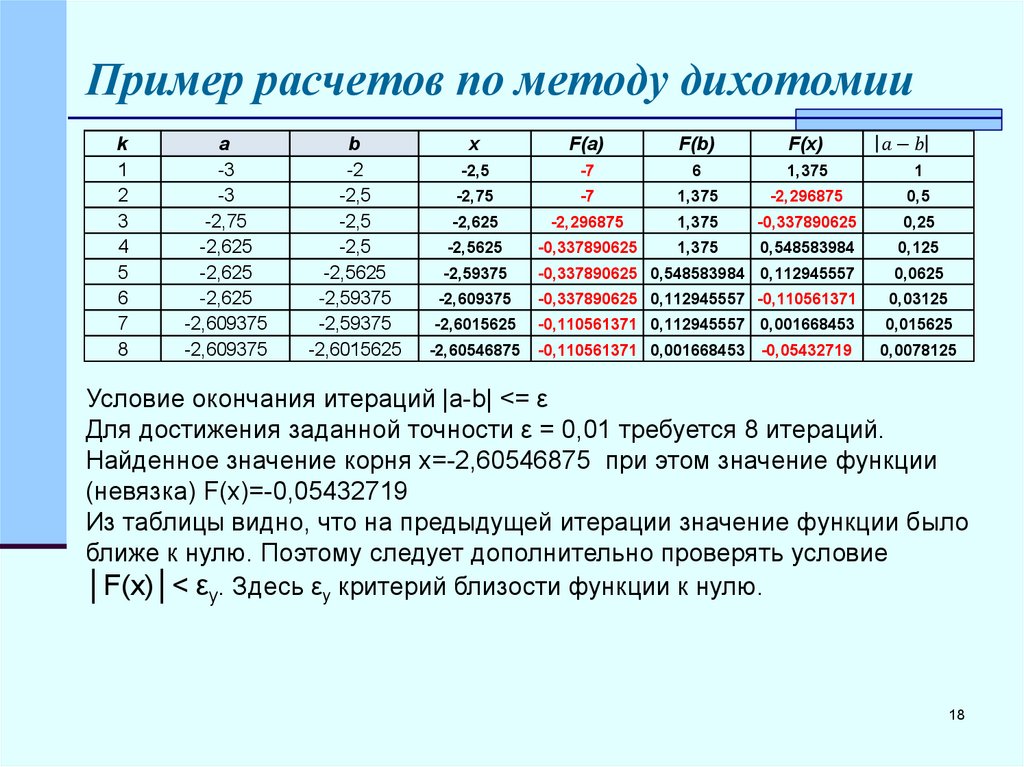
Пример расчетов по методу дихотомииk
1
2
3
4
5
6
7
8
a
-3
-3
-2,75
-2,625
-2,625
-2,625
-2,609375
-2,609375
b
-2
-2,5
-2,5
-2,5
-2,5625
-2,59375
-2,59375
-2,6015625
x
F(a)
F(b)
F(x)
-2,5
-7
6
1,375
1
-2,75
-7
1,375
-2,296875
0,5
-2,625
-2,296875
1,375
-0,337890625
0,25
-2,5625
-0,337890625
1,375
0,548583984
0,125
-2,59375
-0,337890625 0,548583984 0,112945557
0,0625
-2,609375
-0,337890625 0,112945557 -0,110561371
0,03125
-2,6015625
-0,110561371 0,112945557 0,001668453
0,015625
-2,60546875
-0,110561371 0,001668453 -0,05432719
0,0078125
Условие окончания итераций |a-b| <= ε
Для достижения заданной точности ε = 0,01 требуется 8 итераций.
Найденное значение корня x=-2,60546875 при этом значение функции
(невязка) F(x)=-0,05432719
Из таблицы видно, что на предыдущей итерации значение функции было
ближе к нулю. Поэтому следует дополнительно проверять условие
│F(x)│< εy. Здесь εy критерий близости функции к нулю.
18
19.
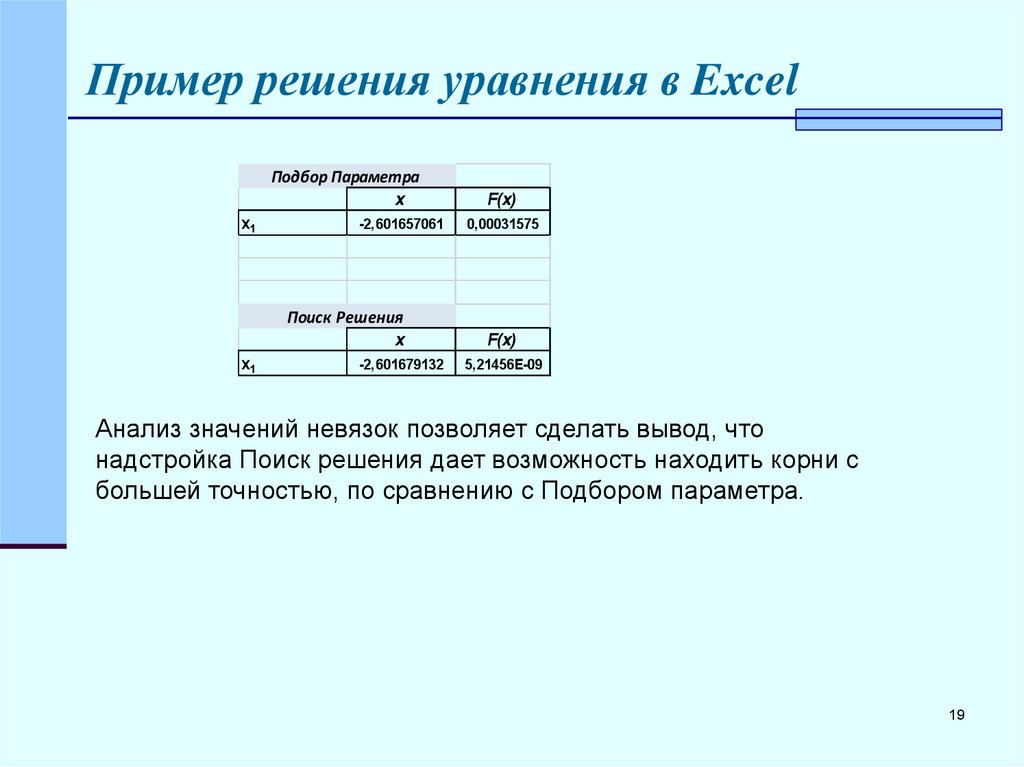
Пример решения уравнения в ExcelПодбор Параметра
x1
x
F(x)
-2,601657061
0,00031575
Поиск Решения
x1
x
F(x)
-2,601679132
5,21456E-09
Анализ значений невязок позволяет сделать вывод, что
надстройка Поиск решения дает возможность находить корни с
большей точностью, по сравнению с Подбором параметра.
19
20.
Метод хордРассматриваемый
метод,
как
и
метод
дихотомии предназначен для уточнения корня
на интервале [a,b], на концах которого
функция принимает разные знаки.
В отличие от метода дихотомии приближенное
значение корня берем не в середине отрезка
[a,b], а в точке x, где ось абсцисс пересекает
прямая,
проведенная
через
точки
с
координатами (a,F (a)), (b,F (b)).
20
21.
Метод хордВ качестве нового интервала для продолжения
итерационного процесса выбираем тот из двух
отрезков ( [a,x] или [x,b] ), на концах которого
функция f(x) принимает значения с разными знаками.
Заканчиваем процесс уточнения корня, когда
расстояние между очередными приближениями станет
меньше заданной погрешности ε,
т.е. │xn - xn-1│< ε,
или когда │f(x)│< εy
21
22.
Метод хордF(b)
КОРЕНЬ
x2
0
F(a)
a
xn+1xn
x1
b
23.
Метод хордОчередное приближение корня определяется по формуле
x=


















 mathematics
mathematics








