Постановка задачи локализации корней. Численные методы решения уравнений

1. Постановка задачи локализации корней. Численные методы решения уравнений

2. Основные требования к алгоритмам и программному обеспечению

Реальный вычислительный алгоритм складывается из двух частей: абстрактного
алгоритма, формулируемого в общепринятых математических терминах, и программы,
записанной на одном из алгоритмических языков и предназначенной для реализации на
ЭВМ.
К вычислительным алгоритмам, предназначенным для широкого использования,
предъявляется ряд весьма жестких требований.

3. Корректность

Алгоритм называется корректным, если соблюдены три условия. Первое – после
выполнения конечного числа элементарных операций любые входные данные
преобразуются в результат (выходные данные). Второе – полученный результат устойчив
по отношению к малым возмущениям входных данных. Это означает, что результат
непрерывным образом зависит от входных данных при условии, что отсутствует
вычислительная погрешность. Отсутствие такой устойчивости делает алгоритм
непригодным для использования на практике. Третье – результат обладает
вычислительной устойчивостью, т.е. вычислительная погрешность стремиться к нулю при
стремлении к нулю погрешности численного метода. Если не выполняется хотя бы одно из
этих условий, то алгоритм называют некорректным.

4. Обусловленность. 

Обусловленность.
Отражает чувствительность результата работы к малым, но совершенно неизбежным
ошибкам округления. Вычислительный алгоритм называют хорошо обусловленным, если
малые относительные погрешности округления приводят к малой относительной
погрешности результата, и плохо обусловленным, если вычислительная погрешность может
быть недопустимо большой.

5. Экономичность

Экономичность – это число элементарных операций, необходимых для реализации
алгоритма. Часто это требование формулируется как требование максимальной быстроты
исполнения алгоритма, что особенно важно при массовых расчетах.

6. Точность

Означает, что алгоритм должен давать решение задачи с заданной или приемлемой
точностью.

7. Надежность программы 

Надежность программы
Означает, что она не содержит ошибок и вычисляет именно тот результат, для которого она
предназначена.

8. Работоспособность (робастность) 

Работоспособность (робастность)
Включает в себя надежность и предполагает, что программа способна выявлять
недопустимые исходные данные, обнаруживать критические для задачи или алгоритма
ситуации

9. Переносимость (портабельность) 

Переносимость (портабельность)
Означает, что программа может работать на различных ЭВМ без изменения или с
незначительными изменениями. Желательно, чтобы любая характеристика ЭВМ,
используемая в программе, либо вычислялась самой программой, либо задавалась
пользователем.

10. Поддерживаемость

Это прежде всего требование легкости модификации, т.е. существование возможности
внесения в программу изменений с минимальной вероятностью появления ошибок, она
должна быть составлена максимально просто, ясно и логично. Зачастую разобраться в
плохо составленной программе бывает гораздо сложнее, чем написать новую. Данное
требование также включает и хорошую документацию (описание) программы.

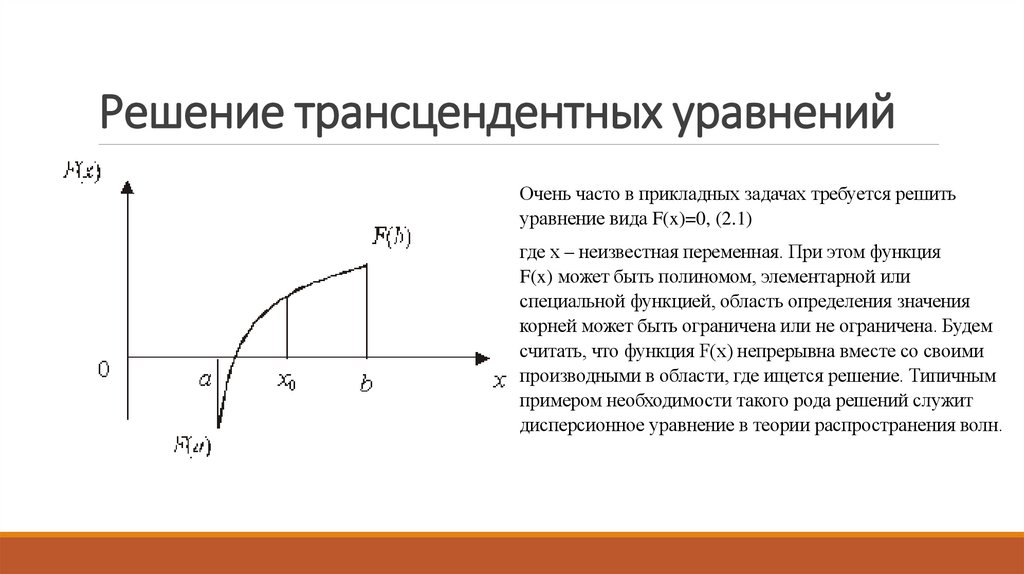
11.   Решение трансцендентных уравнений

Решение трансцендентных уравнений
Очень часто в прикладных задачах требуется решить
уравнение вида F(x)=0, (2.1)
где x – неизвестная переменная. При этом функция
F(x) может быть полиномом, элементарной или
специальной функцией, область определения значения
корней может быть ограничена или не ограничена. Будем
считать, что функция F(x) непрерывна вместе со своими
производными в области, где ищется решение. Типичным
примером необходимости такого рода решений служит
дисперсионное уравнение в теории распространения волн.

12. Решение трансцендентных уравнений

Численное решение уравнения вида (2.1) предполагает выполнение двух этапов. На
первом этапе, определяется количество корней уравнения в искомом интервале значений
переменной x. Лучше всего этот этап реализовывать не программным, а интерактивным
образом (построить график и визуально определить количество корней и их
местонахождение). Искомый корень следует изолировать, выбрав интервал, на котором
он является единственным. Такой интервал называют интервалом изоляции корня. На
втором этапе определяется этот изолированный корень. Напомним, что корнем уравнения
(2.1) называется такое значение переменной x, при котором уравнение обращается в
тождество.

13. Метод дихотомии (деления отрезка пополам)

Допустим, что каким-либо способом определен отрезок [a,b] изоляции корня. Это
означает, что график функции F(x) пересекает ось абсцисс (Рис.2.1), т.е. значения F(a) и
F(b) имеют разные знаки. (Если график функции касается оси абсцисс, то необходимо
решить уравнение, аналогичное (2.1), но только для производной функции. Этот случай
рассматриваться не будет.) Для определенности будем считать, что F(a)<0, а F(b)>0.
Найдем середину отрезка [a,b] число x0 (нулевое приближение)
(2.2)
Значение F(x0) будет либо меньше нуля, либо больше нуля (если F(x0)=0, то корень
найден). Очевидно, что решение будет лежать на отрезке [a,x0]. Далее найденный
отрезок опять делим пополам и находим первое приближение

14. Метод дихотомии (деления отрезка пополам)

(2.2)
и опять определяем знак F(x1). После n приближений исходный отрезок, на котором
ищется решение, будет уменьшен в 2n раз. Например, после 10 итераций решение будет
находиться в отрезке
длиной ≈10-3(b-a), а после 20 – ≈10-6(b-a).
Вычисления проводятся до тех пор, пока не выполнится условие: |xn+1-xn|≤ε или |F(xn+1)F(xn)|≤ε1.

15. Метод дихотомии (деления отрезка пополам)

Алгоритм
1.
Определяем знаки F(a) и F(b).
2.
Вычисляем нулевое приближение – x0.
3.
Определяем знак F(x0).
4.
Если F(a)F(x0)<0, то определяем новый отрезок, где находится решение – [a,x0], иначе
[x0,b].
5.
Вычисляем первое приближение x1 и т.д.

16. Метод хорд

Одним из вариантов, развивающих метод дихотомии,
является определение приближенного решения методом
хорд. Графически этот метод представлен на рисунке 2.2.
Суть данного метода заключается в том, что приближенное
решение определяется в точке пересечения прямой,
соединяющей концы отрезка [a,b].

17. Метод хорд

Соответственно для нулевого приближения так же будем иметь два
варианта (одинаковыхпо значению)
Далее, как и в методе дихотомии, определяем знак F(x0) и выбираем из
отрезков [a,x0] и [x0,b] тот, у которого знаки функции на концах
различаются. Продолжая этот процесс, находим последовательно второе,
третье и последующие приближения. Выход из процесса приближения и
алгоритм метода хорд такой же, как и для метода дихотомии.

18. Метод простой итерации

Если от уравнения (2.1) перейти к эквивалентному уравнению
x=f(x), (2.9)
то возможно использование итерационной процедуры нахождения корня уравнения. При
этом функцию f(x) часто называют итерационной.
Процедура нахождения корня достаточно проста: выберем какое-либо начальное
приближение x0 и подставим его в уравнение (2.9). В результате получим первое
приближение x1, которое опять подставим в уравнение. Продолжая этот процесс
неограниченно, получим последовательность приближений к корню, вычисляемую по
формуле
xn+1=f(xn) . (2.10)

19. Метод простой итерации

Очевидно, что если существует предел последовательности
f(x) непрерывна, то получим равенство
и функция
x*=f(x*), (2.11)
а это значит, что x* – корень уравнения (2.9). Отметим, что метод простой итерации
является одношаговым.

20. Метод простой итерации

Геометрическая интерпретация метода представлена на рис.2.3. Из рисунка видно, что
метод простой итерации может приводить как к сходящейся к решению процедуре, так и к
расходящейся.

21. Метод простой итерации

Для использования этого метода необходимо установить критерий его сходимости. Будем
считать, что в итерационной формуле (2.10)
(2.12)
где εn и εn+1 – отклонения n-го и (n+1)-го приближения от корня x*. Если процесс уточнения
осуществляется вблизи корня x*, то функцию f(x) приближенно можно представить в виде
первых двух членов разложения в ряд Тейлора.

22. Метод простой итерации

Используя выражение (2.11), получаем
(2.13)
Принимая во внимание равенство (2.11), имеем
(2.14)

23. Метод простой итерации

Для обеспечения сходимости итерационного процесса необходимо потребовать, чтобы
, что приводит к условию
(2.15)
, откуда

24. Метод простой итерации

Зная условие сходимости итерационного процесса (2.15), можно разработать процедуру
перехода от уравнения (2.1) к уравнению (2.9) так, чтобы итерационный процесс сходился
наиболее эффективным образом. Для этого умножим обе части равенства (2.1) на некоторую
константу α и прибавим x, получим
x=x+αF(x). (2.16)
Таким образом, искомая функция f(x) будет иметь вид
f(x)=x+αF(x). (2.17)
Произвольный параметр α выбирается так, чтобы было обеспечено условие сходимости.
Наиболее удобно выбрать этот параметр из условия
для обеспечения
двухсторонней сходимости, при этом критерий окончания итерационного процесса будет
наиболее простым
|xn+1-xn|<ε. (2.18)
Наибольшая скорость сходимости будет, когда
, то есть

25. Метод Ньютона

Одним из наиболее эффективных методов нахождения корней уравнения (2.1) является
метод Ньютона, расчетное соотношение которого можно получить, используя два
различных подхода.

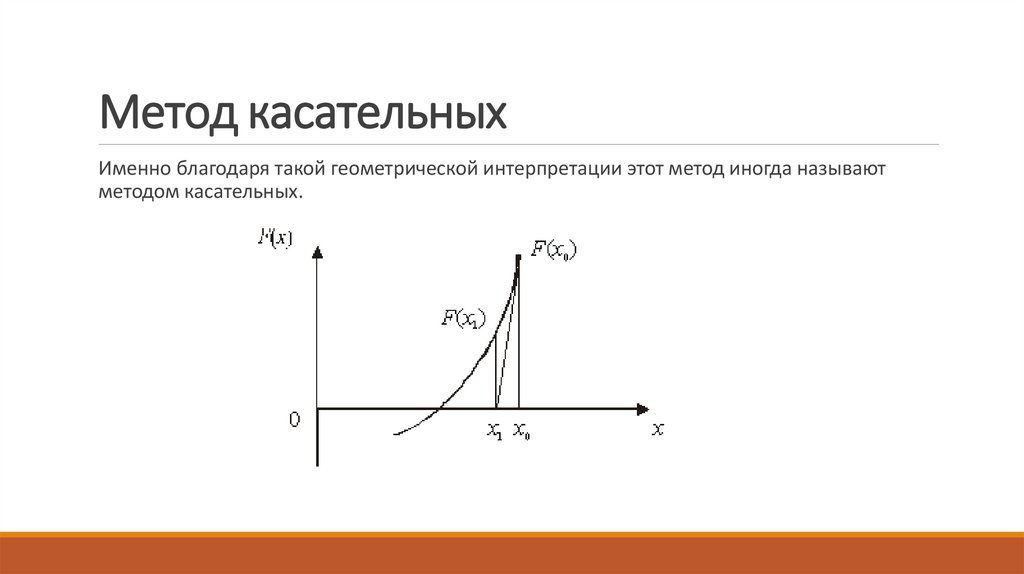
26. Метод касательных

Допустим, найдено некоторое начальное приближение x0 к решению уравнения. В точке с
координатами (x0,F(x0)) проводим касательную к графику функции F(x), затем находим
точку пересечения этой касательной с осью абсцисс – это будет первое
приближение x1 (рис.2.4). Строя касательную в точке (x1,F(x1)) и находя точку ее
пересечения с осью Ox, определяем второе приближение x2. Продолжая этот процесс,
получаем последовательность приближений x0,x1,…,xn,… к корню уравнения (2.1).

27. Метод касательных

28. Метод касательных

Именно благодаря такой геометрической интерпретации этот метод иногда называют
методом касательных.

29. Метод линеаризации

Если определена некоторая достаточно малая область нахождения решения, то любую
сложную кривую в этой области приближенно можно заменить на прямую, т.е. провести
линеаризацию функции в данной области. Используя эту процедуру, можно свести
решение исходного нелинейного уравнения к последовательному решению линейных
уравнений.

30. Метод линеаризации

31. Метод линеаризации

Алгоритм
1.
Локализуем корень.
2.
Выбираем начальное приближение x0.
3.
Вычисляем производную в точке x0.
4.
Вычисляем следующее приближение по формуле (2.21).
В качестве примера программной реализации возьмем уравнение (2.3). Будем искать
решение с точностью не более 10-6 на отрезке [0,1], где, как было показано, находится
только один корень. С учетом соотношение (2.21), получим следующую итерационную
формулу:

32. Модификации метода Ньютона

Модификации метода Ньютона направлены в основном на исключение из итерационных
процедур вычисления производной. При этом итерационные методы решения
нелинейных уравнений, предлагаемые в этом параграфе (безусловно, не все), по существу
используют некоторую процедуру линеаризации.

33. Упрощенный метод Ньютона

Допустим, некоторым методом, например, методом дихотомии, найдена достаточно
малая окрестность решения уравнения (2.1). Если производная F’(x) в этой окрестности
непрерывна, то ее значение вблизи корня x* практически постоянно. Поэтому можно лишь
однажды вычислить производную только в точке начального (или какого угодно)
приближения, а затем заменить в формуле (2.21) F’(xn) на значение F’(x0). В результате
получается расчетная формула упрощенного метода Ньютона
Упрощение вычислений достигается за счет резкого падения скорости сходимости.

34. Метод секущих

35. Метод секущих

36. Метод ложного положения

В упрощенном методе Ньютона используем производную, вычисленную лишь в одной
точке. Если в методе секущих вместо приближения xn-1 взять некоторое постоянное
значение с, то вычислительная процедура нахождения решения нелинейного уравнения
(2.1) существенно упрощается. При этом, безусловно, значение с должно быть выбрано
таким образом, чтобы оно находилось вблизи корня уравнения. Расчетное соотношение
принимает вид
Метод становится одношаговым: требуется лишь одно начальное приближение, однако
при этом, конечно, скорость сходимости уменьшается.