Similar presentations:
Диэлектрик, свойства. Методы испытания диэлектриков (лекция 3 - 4)
1.
Методы испытания материаловДиэлектрик, свойства. Методы
испытания диэлектриков
Лекция 3-4
1
2.
Слайд 23.
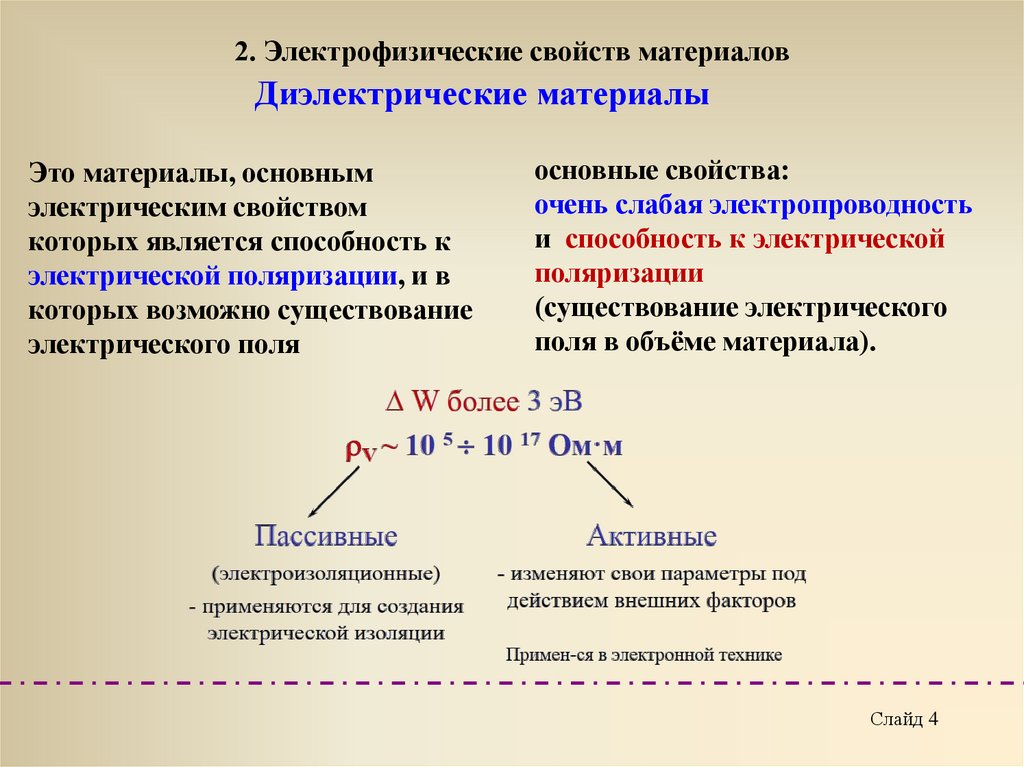
2. Электрофизические свойств материаловДиэлектрические материалы
Диэлектрическая проницаемость
Диэлектрическая проницаемость состоит из действительной и мнимой части.
Вещественная часть называется диэлектрической постоянной и характеризует
запас энергии электрических колебаний в диэлектрике, а мнимая часть –
фактором диэлектрических потерь.
Потери представляют ту часть энергии, которая рассеивается в диэлектрике в
виде теплоты. На рисунке представлена векторная диаграмма для получения tgδ
Слайд 3
4.
2. Электрофизические свойств материаловДиэлектрические материалы
Это материалы, основным
электрическим свойством
которых является способность к
электрической поляризации, и в
которых возможно существование
электрического поля
основные свойства:
очень слабая электропроводность
и способность к электрической
поляризации
(существование электрического
поля в объёме материала).
Слайд 4
5.
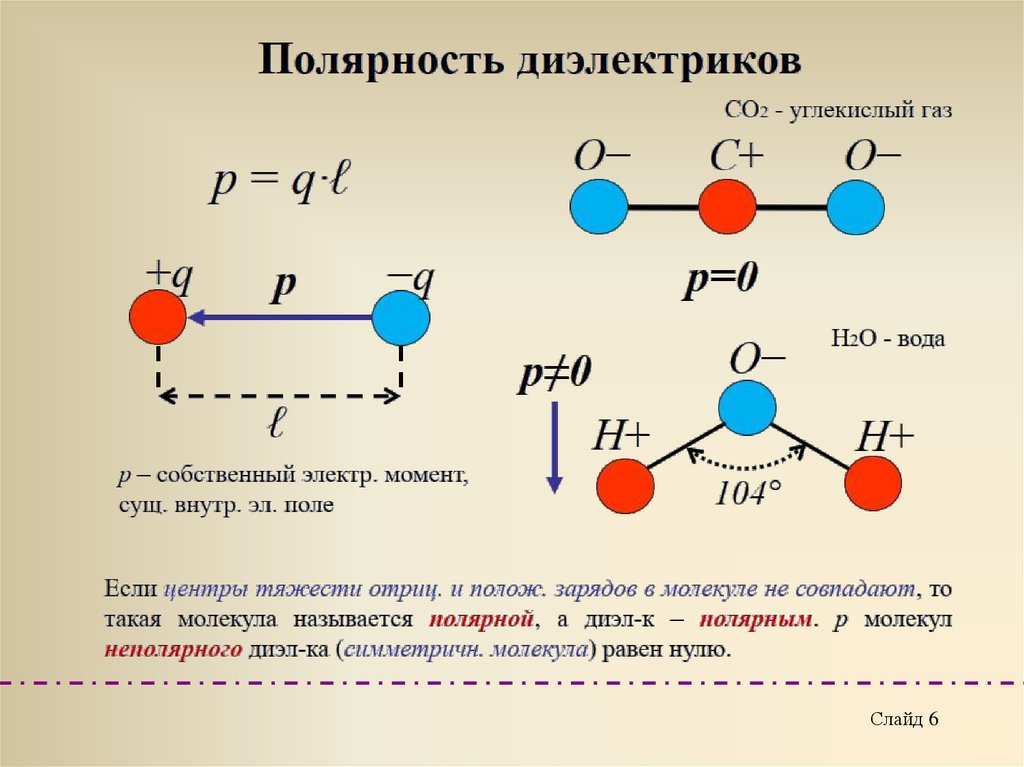
Слайд 56.
Слайд 67.
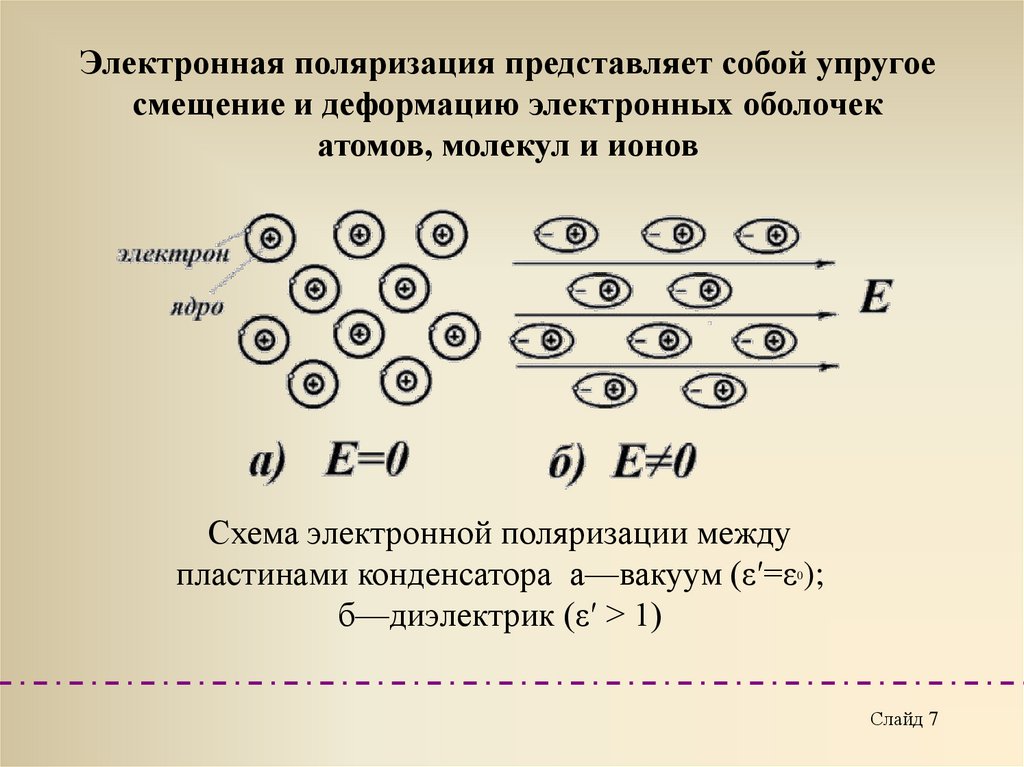
Электронная поляризация представляет собой упругоесмещение и деформацию электронных оболочек
атомов, молекул и ионов
Схема электронной поляризации между
пластинами конденсатора а—вакуум (ε′=ε );
б—диэлектрик (ε′ > 1)
0
Слайд 7
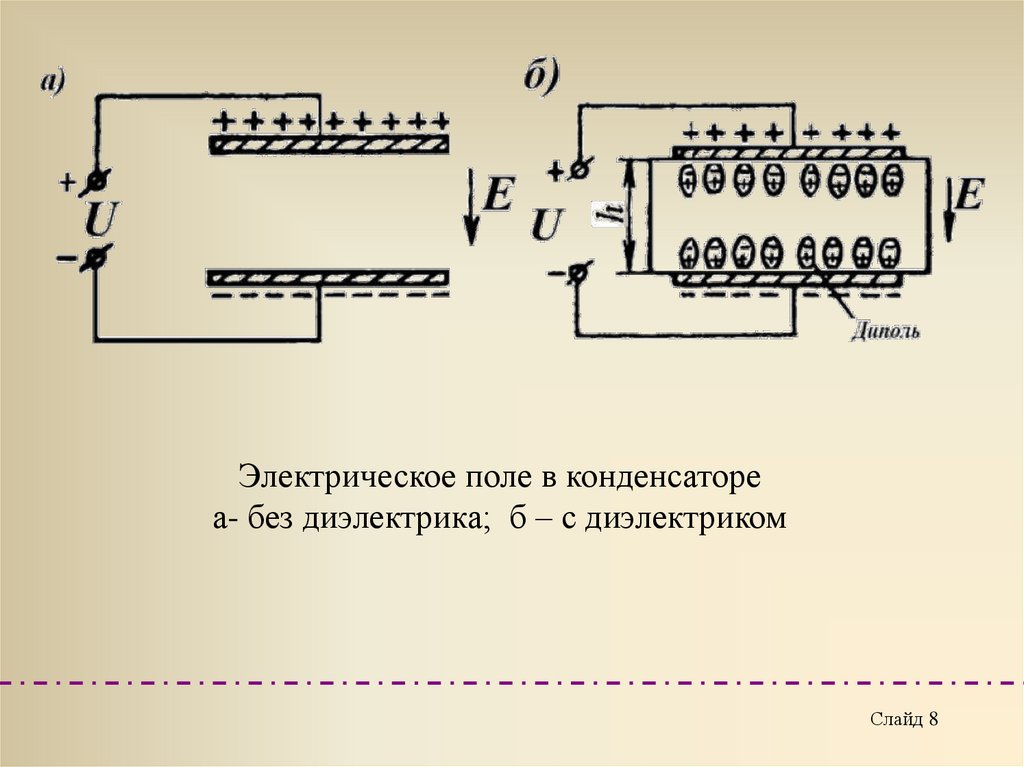
8.
Электрическое поле в конденсатореа- без диэлектрика; б – с диэлектриком
Слайд 8
9.
Поляризацию вещества численно характеризуют векторомэлектрического смещения
D=εaE =εoε′E,
где εa и ε′ – абсолютная и относительная диэлектрические
проницаемости вещества соответственно.
Относительную диэлектрическую проницаемость ε
можно определить как отношение емкости конденсатора с
данным диэлектриком С к емкости того же конденсатора,
но без диэлектрика, а с вакуумом Со : ε′ = С / Со.
Слайд 9
10.
Время установления электронной поляризации τсоставляет около 10-14 – 10-15 с. Таким образом, электронная
поляризация устанавливается практически мгновенно.
В диапазоне 0÷1014 Гц диэлектрическая проницаемость
практически не зависит от частоты, и поляризация не связана
с потерями энергии электрического поля.
При частотах 1014–1015 Гц проявляются резонансные потери
энергии.
Величина ε′ вещества с чисто электронной поляризацией
равна квадрату показателя преломления света
ν (ε′=ν2) и обычно не превышает значений 2–2,5.
Слайд 10
11.
Исключительно электронную поляризацию имеютнеполярные вещества:
газообразные (водород, кислород, азот), жидкие
(нефтяные масла, октол), твердые (парафин, церезин,
полиэтилен, политетрафторэтилен и др.).
Электронная поляризация наблюдается также и во всех
остальных диэлектриках, но у большинства из них на
электронную поляризацию накладываются другие виды
поляризации.
Слайд 11
12.
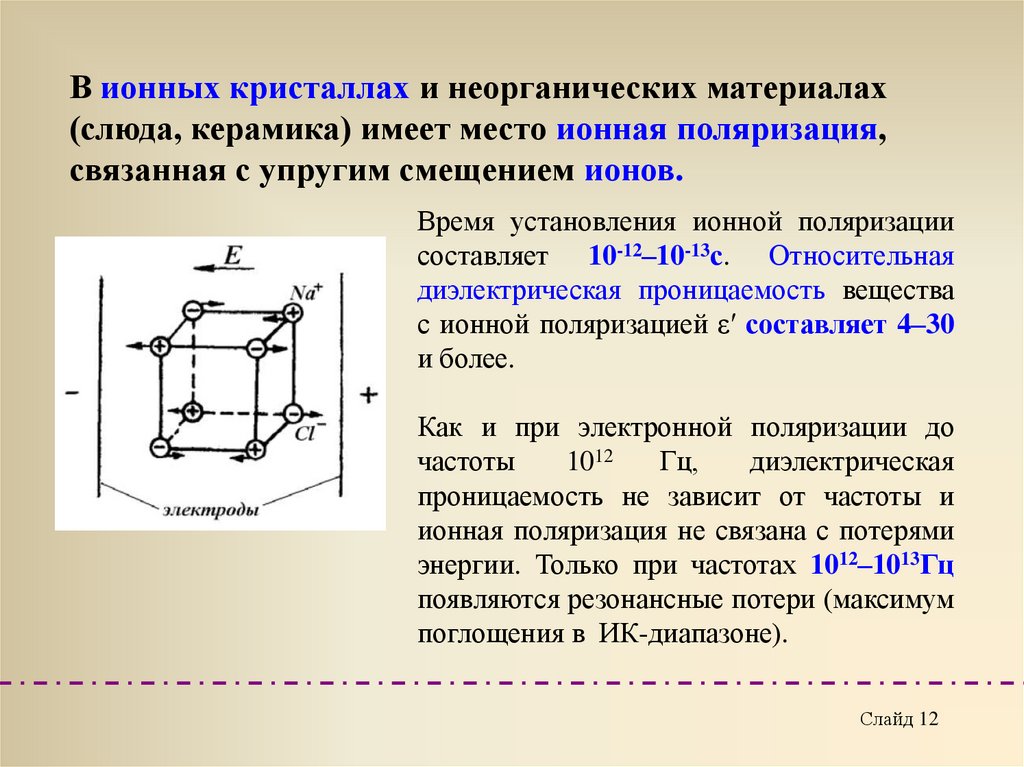
В ионных кристаллах и неорганических материалах(слюда, керамика) имеет место ионная поляризация,
связанная с упругим смещением ионов.
Время установления ионной поляризации
составляет 10-12–10-13с. Относительная
диэлектрическая проницаемость вещества
с ионной поляризацией ε′ составляет 4–30
и более.
Как и при электронной поляризации до
частоты
1012
Гц,
диэлектрическая
проницаемость не зависит от частоты и
ионная поляризация не связана с потерями
энергии. Только при частотах 1012–1013Гц
появляются резонансные потери (максимум
поглощения в ИК-диапазоне).
Слайд 12
13.
В случае полярных диэлектриков, когда молекулы имеютнесимметричное строение и обладают дипольным моментом,
происходит дипольная поляризация. При этом виде поляризации
дипольные молекулы (диполи), находящиеся в хаотическом тепловом
движении, частично ориентируются под действием внешнего
электрического поля
Время установления дипольно-релаксационной
поляризация составляет 10-8– 10-6 с и более. Такой
тип поляризации характерен прежде всего для
полярных жидкостей. Этот вид поляризации может
наблюдаться также у отдельных твердых веществ,
состоящих из крупных полярных молекул
(полярные полимеры). При этом поляризация
обусловлена поворотом не самой молекулы, а
имеющихся в ней полярных радикалов (ОН, NH3
и др.) по отношению к неподвижной молекуле. Этот
вид поляризации обычно называют дипольнорадикальной (или дипольно-ориентационной).
Слайд 13
14.
Примерами вещества с этим видом поляризации являютсяцеллюлоза, полярность которой объясняется наличием
гидроксильных
групп
—
ОН
и
кислорода,
поливинилхлорид, полярность которого связана с наличием
хлора в молекулах полимера. К полярным диэлектрикам
относятся: полярные газы (НСl, HBr, СО и др.), жидкости
(вода, совол, совтол, касторовое масло), твердые вещества
(полярные
полимеры
–
поливинилхлорид,
полиэтилентерефталат (лавсан), целлюлоза и др.).
2
Величина
относительной
диэлектрической
проницаемости
полярных
диэлектриков
обычно
составляет 3–8, но иногда достигает и нескольких десятков
(например, для воды ε′= 81).
Слайд 14
15.
Миграционная поляризация наблюдается в некоторыхдиэлектриках и системах изоляции, в частности, в
неоднородных диэлектриках, особенно с полупроводящими
включениями.
В случае диэлектрика с полупроводящими включениями
этот вид поляризации заключается в перемещении
(миграции) зарядов в этих включениях до их границ и
накоплении зарядов на границах раздела.
Процессы установления и снятия миграционной
поляризации сравнительно медленны и могут
продолжаться секунды, минуты и даже часы. Поэтому
она обычно наблюдается лишь при весьма низких
частотах.
Слайд 15
16.
Слайд 1617.
Слайд 1718.
Слайд 1819.
Слайд 1920.
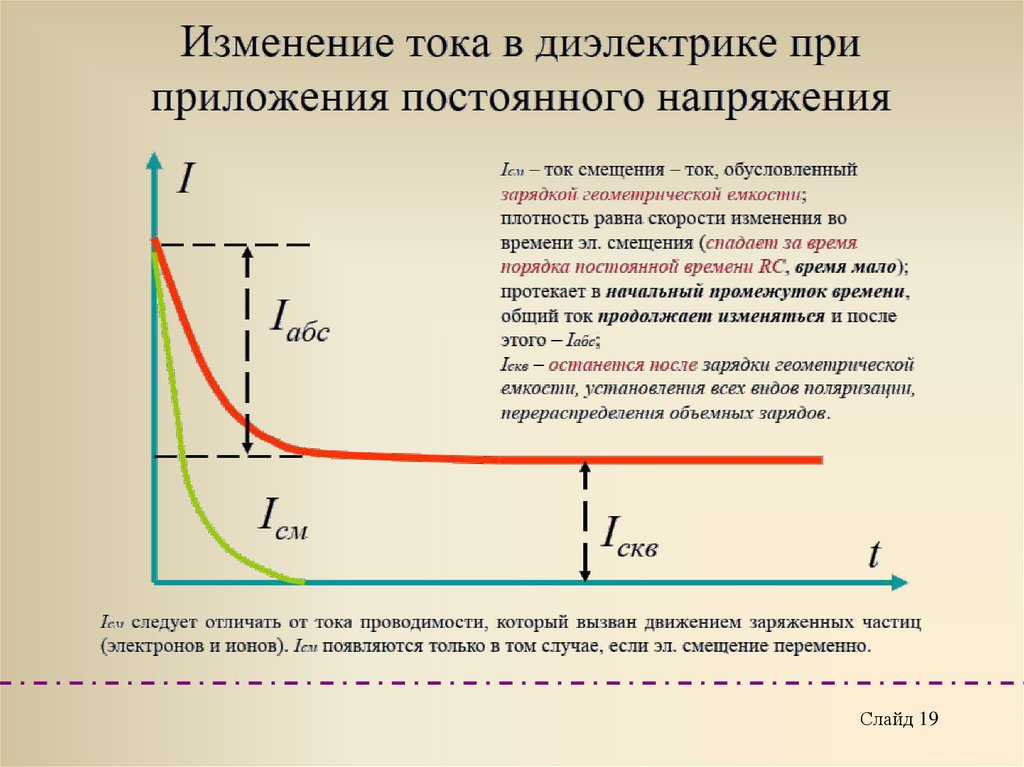
Так смещения и сквозной ток в ПТКСлайд 20
21.
Слайд 2122.
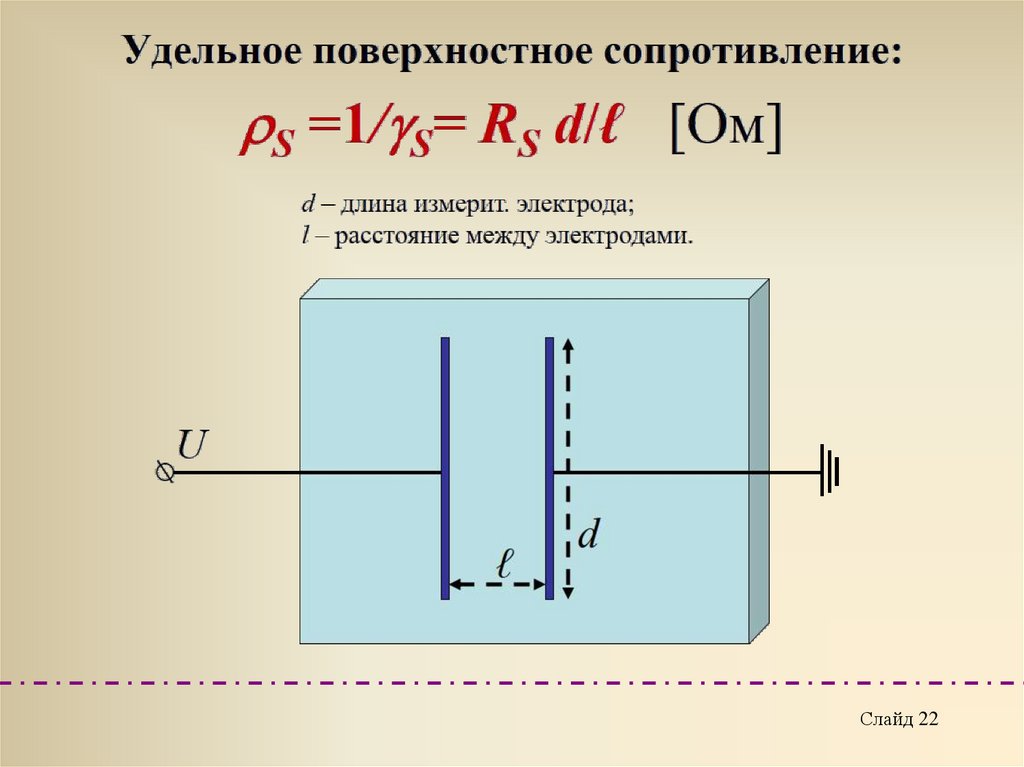
Слайд 2223.
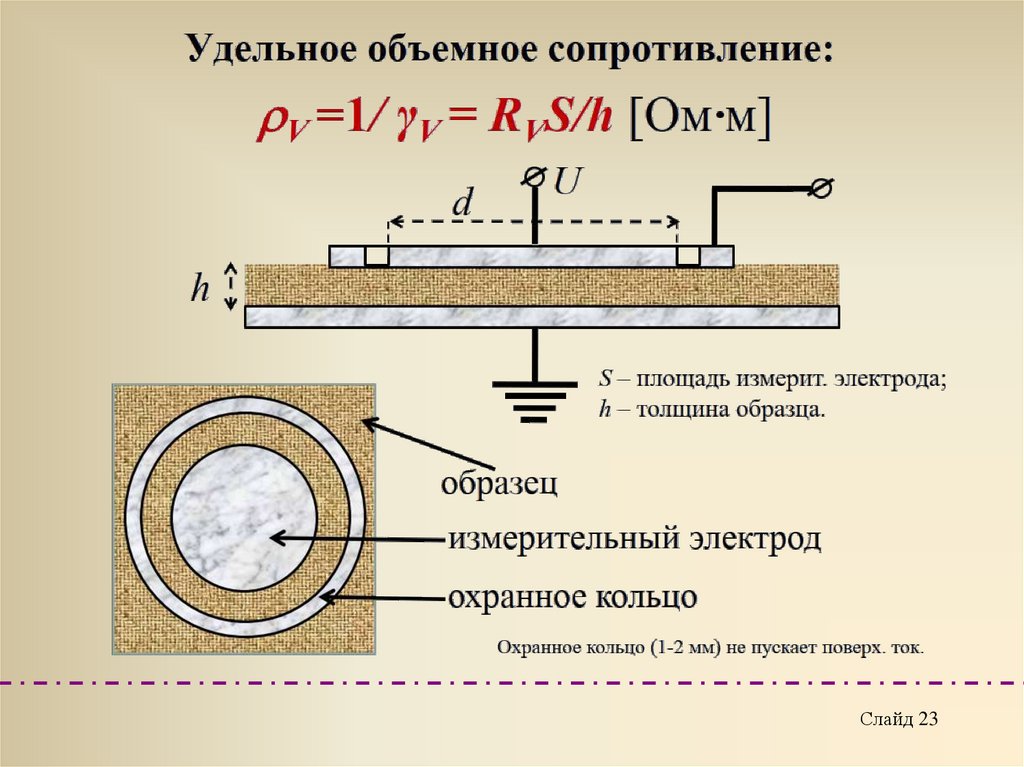
Слайд 2324.
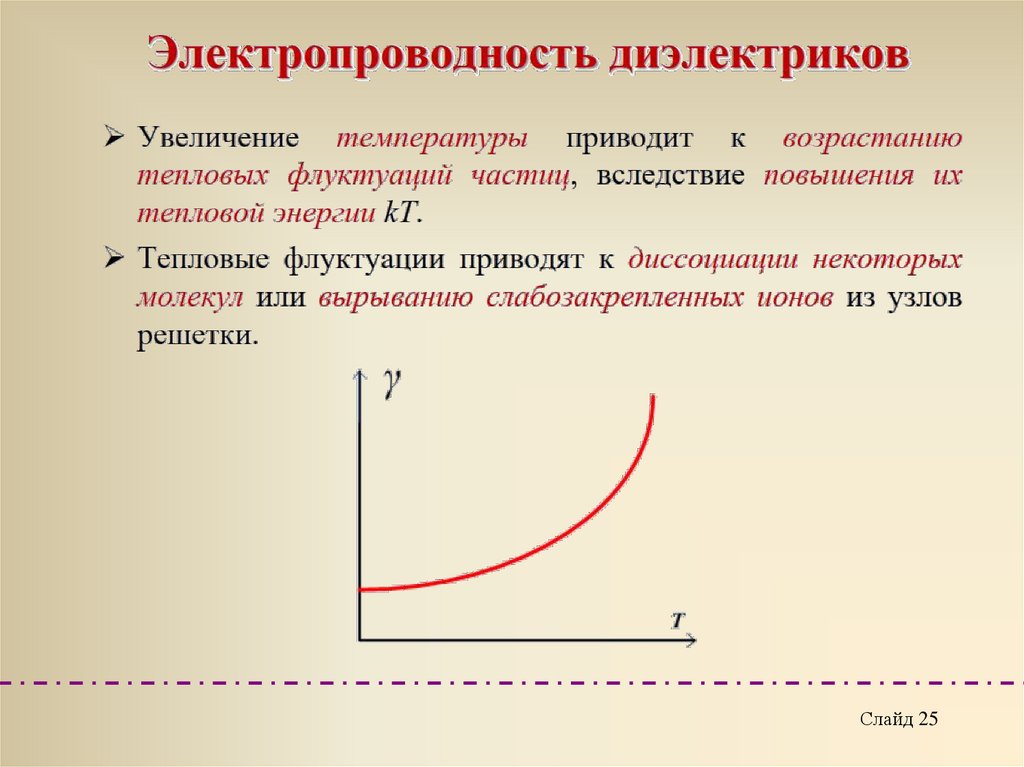
Слайд 2425.
Слайд 2526.
Слайд 2627.
Слайд 2728.
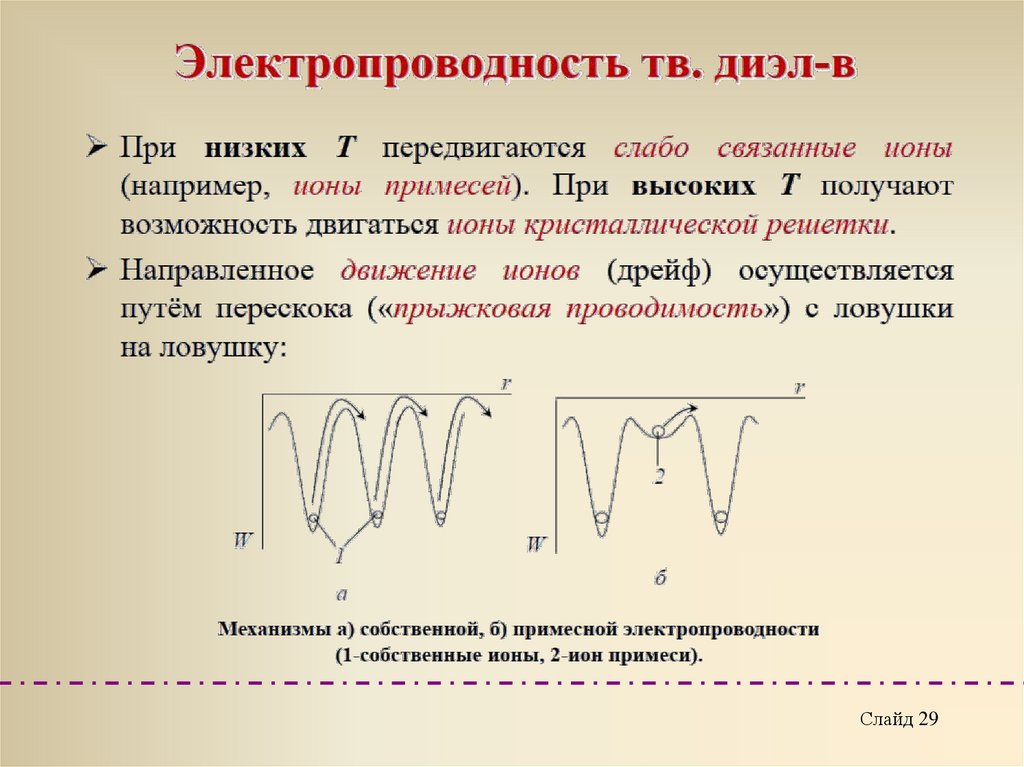
μ - подвижностьСлайд 28
29.
Слайд 2930.
Слайд 3031.
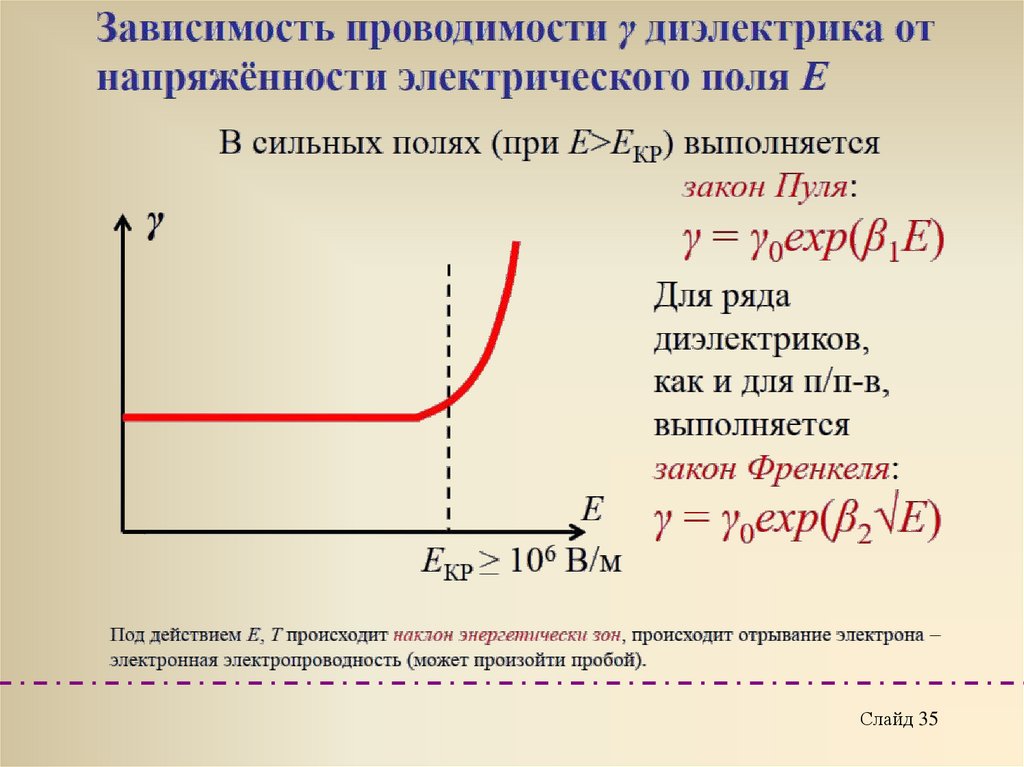
Слайд 3132.
Слайд 3233.
Электропроводностью называется способностьматериала без потерь на выделение тепла проводить
электрический ток.
Хорошей электропроводностью обладают металлы
и их сплавы, особенно медь и алюминий.
Большинство неметаллических материалов не
способны проводить электрический ток, что также
является важным свойством, используемом в
электроизоляционных материалах.
Слайд 33
34.
Слайд 3435.
Слайд 3536.
ASTM D149-20Стандартный метод испытаний напряжения
диэлектрического пробоя и диэлектрической прочности
твердых электроизоляционных материалов на
промышленных частотах
Стандарт ASTM D149-20, разработанный Американским обществом
испытаний и материалов (ASTM), определяет процедуры и методы
испытаний для определения диэлектрической прочности твердых
изоляционных материалов на промышленных частотах питания при
определенных условиях. Если не указано иное, эти испытания
проводятся при 60 Гц. Однако этот метод испытаний также может
выполняться на любой частоте от 25 до 800 Гц. Однако на частотах
выше 800 Гц нагрев диэлектрика представляет собой потенциальную
проблему.
Слайд 36
37.
Диэлектрическая прочность электроизоляционного материалапредставляет интерес для любого приложения, в котором присутствует
электрическое поле. Во многих случаях диэлектрическая прочность
материала является определяющим фактором при проектировании
оборудования, в котором он будет использоваться.
Этот метод тестирования и испытания полезен для контроля процесса,
приемочного или исследовательского тестирования.
Однако полученные результаты в большинстве случаев необходимо
сравнивать и оценивать с результатами других функциональных
испытаний, чтобы определить диэлектрические свойства материала в
реальных условиях применения.
Слайд 37
38.
Величина tgδ является важной характеристикойдиэлектриков. Она определяет диэлектрические потери в
материале: чем больше tgδ, тем более высокие (при
прочих равных условиях) диэлектрические потери. Для
наиболее широко применяемых диэлектриков tgδ имеет
значение в пределах от 0,0001 до 0,03.
О величине диэлектрических потерь участка
изоляции, керамических материалов и некоторых
радиодеталей (конденсаторов, катушек индуктивности и
т.п.) можно судить также по значению их добротности Q
Слайд 38
39.
Диэлектрическими потерями называют мощность,рассеиваемую в диэлектрике при действии на него
переменного электромагнитного поля.
Диэлектрические потери могут быть обусловлены как
токами проводимости (потери проводимости), так и
запаздыванием поляризации при изменении поля
(релаксационные, миграционные и резонансные потери).
Кроме того, в сильных электрических полях при наличии
в диэлектрике воздушных включений наблюдаются
дополнительные потери энергии (ионизационные
потери).
Слайд 39
40.
Конденсатор с идеальным диэлектриком (без потерь) впеременном поле с круговой частотой ω имеет чисто
реактивную (емкостную) проводимость ΥCo=iωC0, так что
на векторной диаграмме емкостный ток через конденсатор
опережает напряжение U на угол π/2.
В реальном конденсаторе в отличие от идеального
реактивная проводимость Υс=iωC и ток сдвинуты по фазе
на угол ϕ. Полный ток I можно разложить на активную
Iа = I sinδ и реактивную Ic = I cosδ составляющие
Слайд 40
41.
Угол δ, дополняющий до 90° угол сдвига фаз ϕ между токоми напряжением в емкостной цепи с реальным диэлектриком,
называют углом диэлектрических потерь.
Углом δ (а чаще tgδ) определяют рассеиваемую в
диэлектрике мощность при переменном электромагнитном
поле.
Таким образом, в случае воздействия переменного
электрического поля диэлектрик характеризуется двумя
основными величинами, одна из которых ε′ определяет его
способность к поляризации, вторая tgδ - диэлектрические
потери:
ε′ =С/C0 = Iа /IC0;
tgδ = Iа /IC.
Слайд 41
42.
Рассмотрим последовательную и параллельнуюэквивалентные схемы диэлектрика и их векторные
диаграммы.
Векторные диаграммы и эквивалентные схемы диэлектрика
с потерями: а – последовательная, б – параллельная.
Слайд 42
43.
Обе схемы эквивалентны друг другу,если при равенстве полных
сопротивлений ZS = ZП = Z будут
равны их активные составляющие.
Это условие соблюдается, если углы
сдвига тока относительно напряжения
равны и значения активной мощности
одинаковы.
Для последовательной схемы замещения имеем:
Активная мощность потерь Рs равна:
Слайд 43
44.
Следовательно, для последовательной схемы:Для параллельной схемы имеем
Активная мощность в этом
случае равна:
Слайд 44
45.
Если у диэлектрика tgδ < 0,1, то величиной tg2 δ можнопренебреч в сравнении с единицей,
и тогда для обеих эквивалентных схем получаются одинаковые
выражения:
Ранее указывалось, если обе схемы эквивалентны друг другу,
тогда Рs = Pp = P и tgδs = tgδ . Эти равенства дают
возможность получить формулы пересчета при переходе от
параллельной схемы замещения к последовательной и
наоборот.
p
Для доброкачественных диэлектриков С ≈ С ≈ C .
р
s
Слайд 45
46.
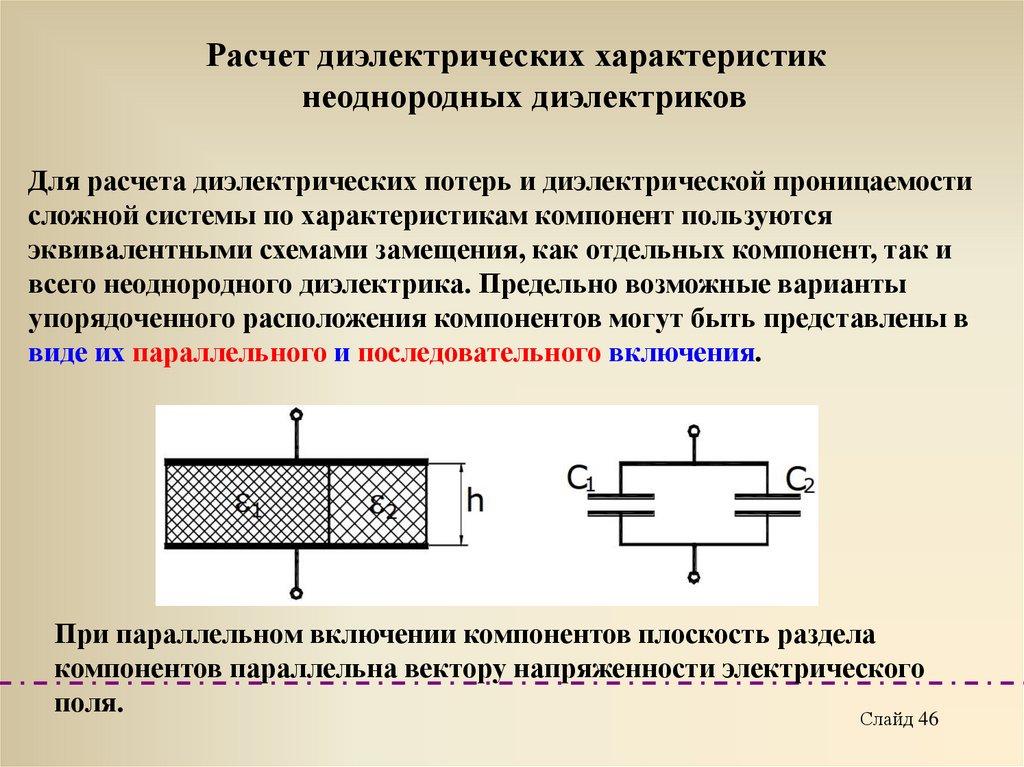
Расчет диэлектрических характеристикнеоднородных диэлектриков
Для расчета диэлектрических потерь и диэлектрической проницаемости
сложной системы по характеристикам компонент пользуются
эквивалентными схемами замещения, как отдельных компонент, так и
всего неоднородного диэлектрика. Предельно возможные варианты
упорядоченного расположения компонентов могут быть представлены в
виде их параллельного и последовательного включения.
При параллельном включении компонентов плоскость раздела
компонентов параллельна вектору напряженности электрического
поля.
Слайд 46
47.
Емкость конденсатора:При одинаковой толщине диэлектриков их объемные концентрации θ
составляют соответственно для первого θ1 и второго θ2 диэлектрика
Часный случай формулы Лихтенеккера
Слайд 47
48.
Если неоднородный диэлектрик состоит не из двух, а изнескольких компонентов, то уравнение имеет вид:
Диэлектрические потери в таком неоднородном диэлектрике
складываются из потерь в компонентах
где Р – активная мощность, рассеиваемая во всем диэлектрике (Вт);
Р1 и Р2 – активная мощность, рассеиваемая в компонентах (Вт);
ω - круговая частота, рад/с;
С – емкость конденсатора, Ф;
tg δ - тангенс угла диэлектрических потерь неоднородного диэлектрика;
U – напряжение на электродах, В.
Слайд 48
49.
При параллельном включении диэлектриков к каждомукомпоненту приложено одинаковое напряжение, поэтому
где tg δ1 и tg δ2 – тангенсы углов диэлектрических потерь компонентов.
Тогда следует, что тангенс угла диэлектрических потерь
двухкомпонентного диэлектрика при параллельном соединении равен
Полагая, что
Слайд 49
50.
Если неоднородный диэлектрик состоит из несколькихпараллельно соединенных слоев, тогда уравнение может
быть записано в виде
Слайд 50
51.
При последовательном соединении компонентов плоскостьраздела их перпендикулярна вектору напряженности
электрического поля.
Объемные концентрации
компонентов будут
пропорциональны их
толщинам
Формула является частным случаем формулы Лихтенеккера
Слайд 51
52.
где x – константа, характеризующая пространственное расположениекомпонентов и принимающая значение от x = +1 (для параллельного
включения компонентов) до x = - 1 (последовательное расположение
компонентов).
Формула Лихтенекера широко применяется для расчета
диэлектрической проницаемости мелкодисперсных смесей. Она дает
результаты расчета, достаточно хорошо совпадающие с измеренными
величинами, если ε1 и ε2 не очень сильно отличаются друг от друга.
Большое практическое применение находят мелкодисперсные
хаотические смеси (пластмассы, пенопласты, керамика и др.),
имеющие предельно разупорядоченное строение. Для них можно
принять, что константа x, в формуле Лихтенекера стремится к нулю.
Чтобы избавиться от неопределенности, продифференцируем это
уравнение по x
Слайд 52
53.
Примем x = 0 и тогда получитсяЭто так называемый логарифмический закон смешения.
Если неоднородный диэлектрик состоит из более чем двух компонентов,
то формулы приводятся к виду:
Слайд 53
54.
Для смесей типа пенопластов, поропластов, пенокерамики и другихпористых материалов, состоящих из твердого и газообразного
диэлектрика, удобнее пользоваться не объемными концентрациями
компонентов, а их массовым содержанием в смеси. Плотность смеси
можно рассчитать на основании арифметического закона смешения:
Где:
ρ1 – плотность монолитного (сплошного) диэлектрика;
ρ – плотность смеси (пенопласта и т.д.).
Слайд 54
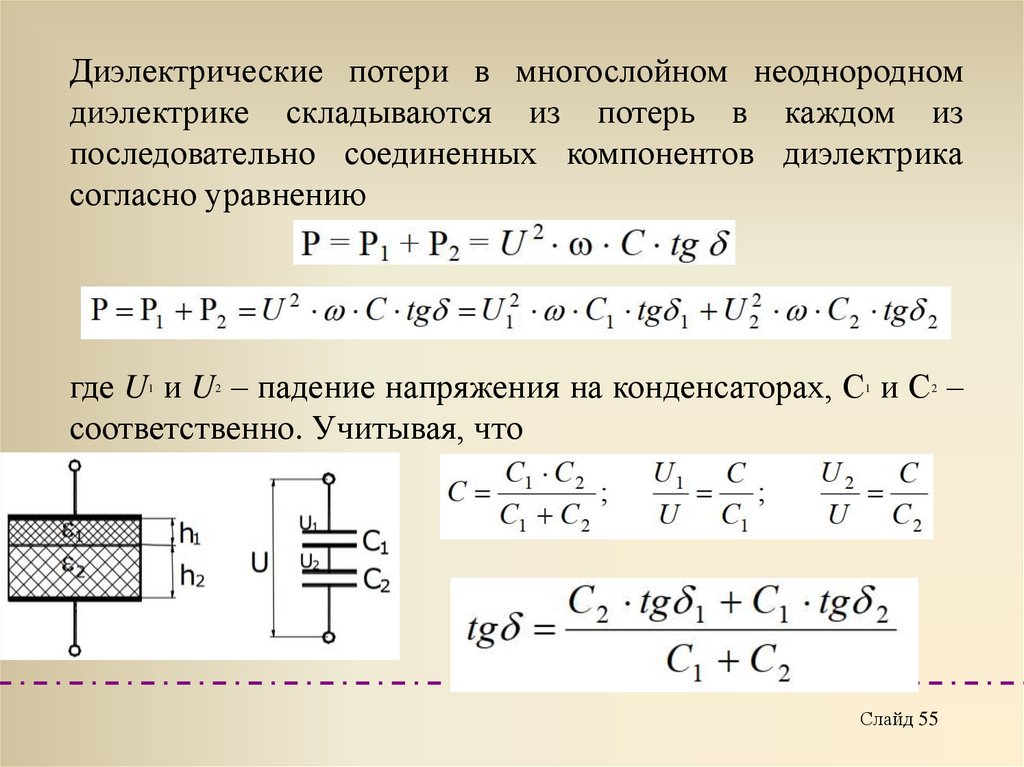
55.
Диэлектрические потери в многослойном неоднородномдиэлектрике складываются из потерь в каждом из
последовательно соединенных компонентов диэлектрика
согласно уравнению
где U и U – падение напряжения на конденсаторах, С и С –
соответственно. Учитывая, что
1
2
1
2
Слайд 55
56.
Слайд 5657.
Слайд 5758.
Принимая во внимание удвоенную толщинуподклеивающего слоя и уравнения
И формулу
можно записать в виде:
Слайд 58
59.
Далее учитываяМожно рассчитать
Слайд 59
60.
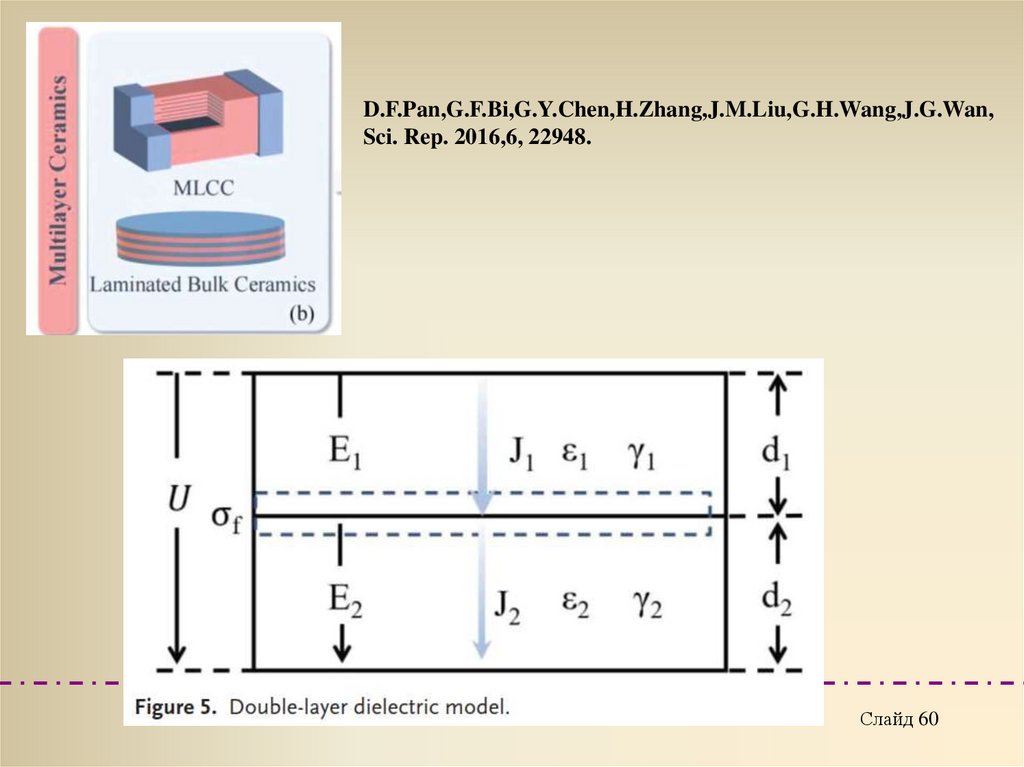
D.F.Pan,G.F.Bi,G.Y.Chen,H.Zhang,J.M.Liu,G.H.Wang,J.G.Wan,Sci. Rep. 2016,6, 22948.
Слайд 60
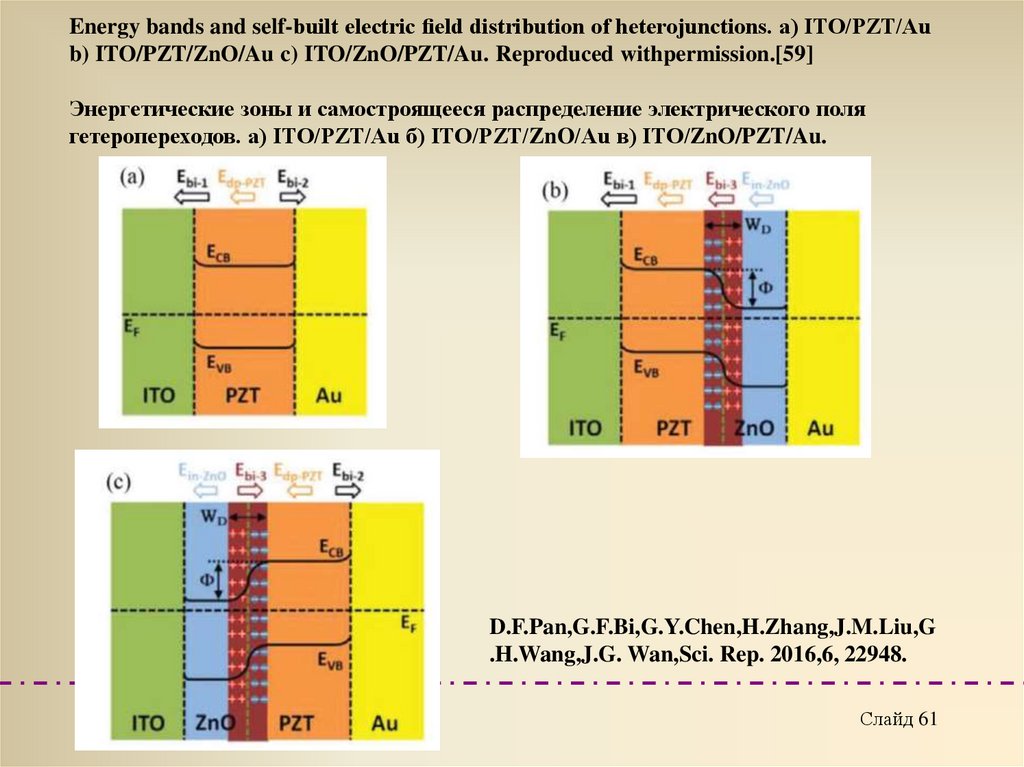
61.
Energy bands and self-built electric eld distribution of heterojunctions. a) ITO/PZT/Aub) ITO/PZT/ZnO/Au c) ITO/ZnO/PZT/Au. Reproduced withpermission.[59]
Энергетические зоны и самостроящееся распределение электрического поля
гетеропереходов. а) ITO/PZT/Au б) ITO/PZT/ZnO/Au в) ITO/ZnO/PZT/Au.
D.F.Pan,G.F.Bi,G.Y.Chen,H.Zhang,J.M.Liu,G
.H.Wang,J.G. Wan,Sci. Rep. 2016,6, 22948.
Слайд 61
62.
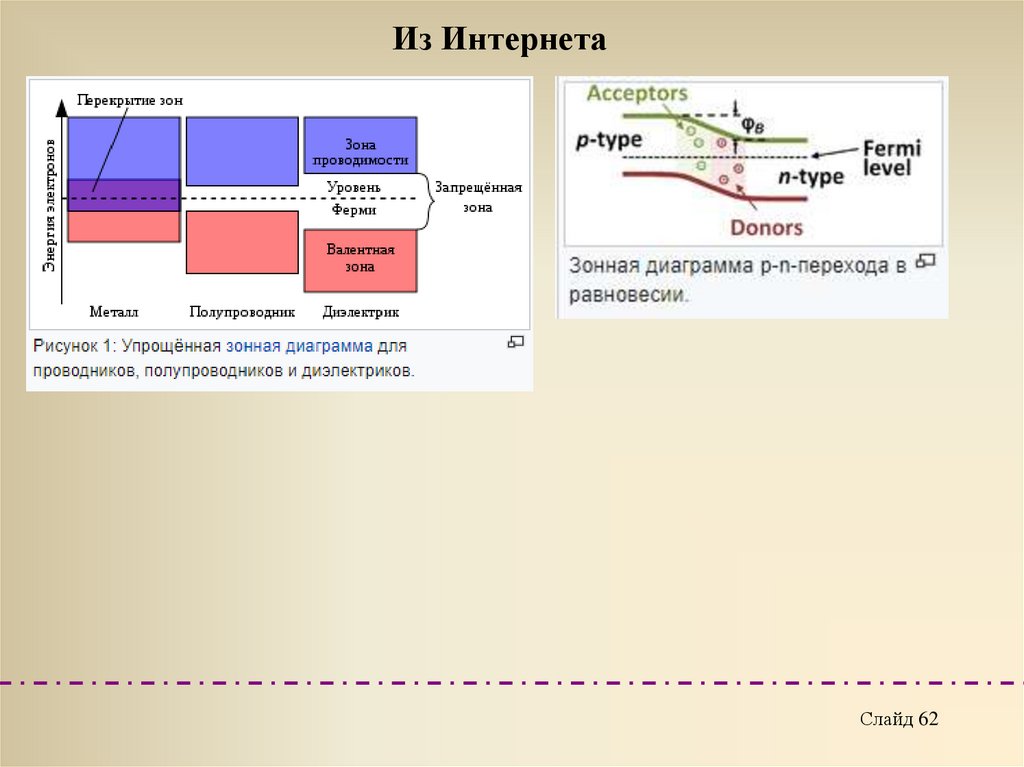
Из ИнтернетаСлайд 62
63.
Слайд 6364.
Где ω = 2πf, ε0 - диэлектрическая проницаемостьвакуума; s и l — площадь электрода и толщина
таблетки (конденсатора) соответственно.
Абсолютная диэлектрическая проницаемость
выражается в кулонах/(вольт*метр) или фарадах/метр
ε0 = 8,8542*10-12 Ф/м
Слайд 64
65.
1Y *
Z
*
Слайд 65
66.
Слайд 6667.
Слайд 6768.
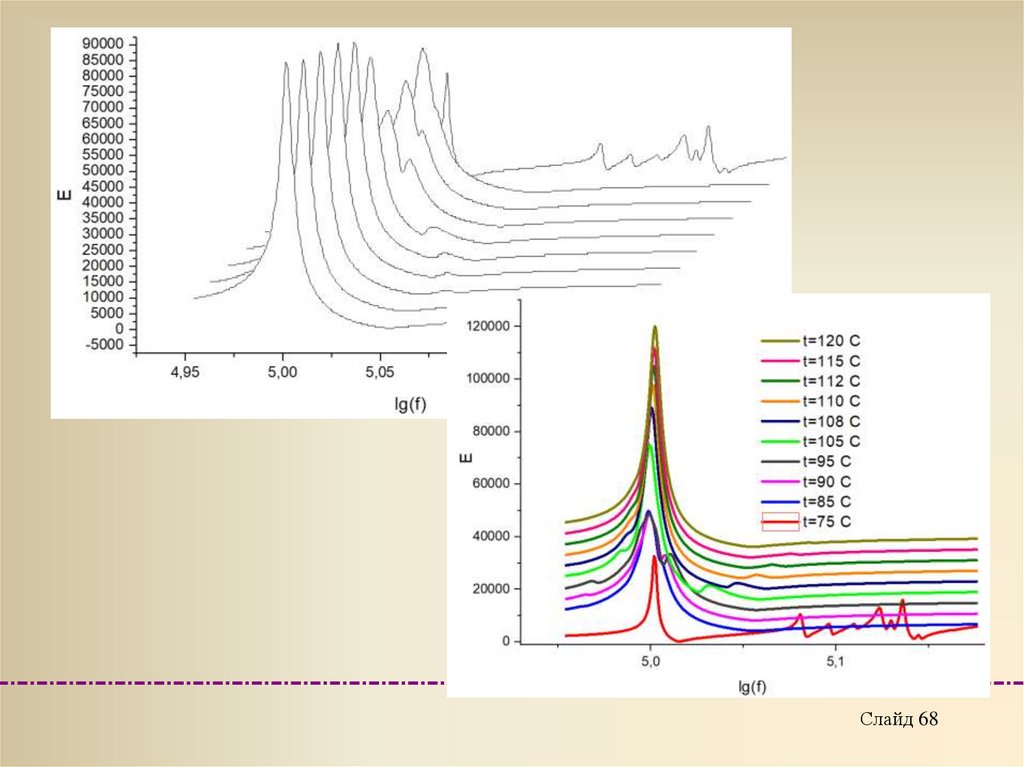
Слайд 6869.
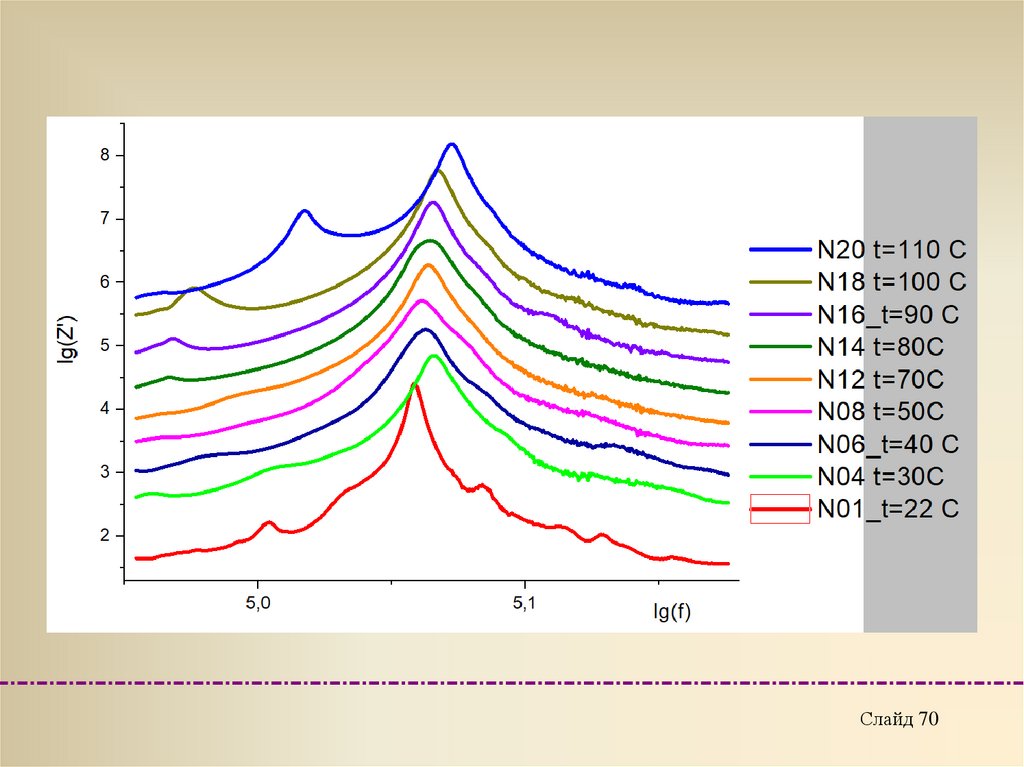
Слайд 6970.
Слайд 7071.
Слайд 7172.
Слайд 7273.
План лекции:Импедансная спектроскопия, основные
понятия
Основные элементы импедансной
спектроскопии
1.Импеданс реального сопротивления
2.Импеданс емкости
3.Импеданс индуктивности
Представление импеданса и адмиттанса в
виде комплексных чисел
Импеданс Варбурга
1.Импеданс Варбурга при диффузии
полубесконечное пространство
2.Импеданс Варбурга при диффузии в
ограниченное пространство
Элемент постоянной фазы (СРЕ)
73
74.
Основная литература1. Импедансная спектроскопия твердых тел: Часть 1: учеб.
пособие / В.Г. Гоффман, А.В. Гороховский, Н.В. Горшков,
Н.Н. Ковынева, Е.В. Колоколова, - Саратов: Сарат. гос. техн.
ун-т, 2017 – 120 с.
2. Поклонский Н.А., Горбачук Н.И. Основы импедансной
спектроскопии композитов. Курс лекций. Минск. БГУ. 2005. –
131с.
3. Иванов-Шиц А.К., Мурин И.В. Ионика твердого тела. т.1.
Изд.СПбГУ, 2000. – 616с.
4. Стойнов З.Б., Графов Б.М., Савова-Стойнова Б., Елкин
В.В. Электро-химический импеданс. – М.: - Наука, 1991. –
336с.
5. Barsoukov E., Macdonald J.R. Impedance spectroscopy
Theory, Experiment end Applications. John Wiley&Sons,
Inc.,Pudlication. 2005. – 595s.
5. Мальдерброт Б.Б. Фрактальная геометрия природы.
М.2002. – 655с.
74
75.
Импедансная спектроскопия, основныепонятия
Импедансная спектроскопия, как
неразрушающий метод входного контроля
Метод электрохимического импеданса является, в отличие,
например, от потенциодинамической вольтамперометрии,
методом низкого уровня, то есть, основан на измерении
отклика электрохимической системы на очень слабые
сигналы, при которых отклонения от равновесного или
стационарного состояния не превышают нескольких
милливольт или даже долей милливольта.
Обычно измерения импеданса проводятся в диапазоне
частот от 0,001 Гц до 1 МГц на импедансметрах Novocontrol,
Elins или Solartron. При этом количество электричества,
проходящего через электрод за полупериод синусоидального
сигнала, не превышает пределы долей микрокулона.
Таким образом, при измерениях импеданса изменения,
происходящие на границе электрод-электролит, затрагивают
лишь малые доли монослоя.
75
76.
При исследовании малопроводящих материалов(диэлектриков), могут применяться высокие значения
измерительных амплитуд.
Так при снятии спектров импеданса диэлектриков или
полупроводников, амплитуды могут достигать сотен и
тысяч вольт. Это оправдано тем, что такие материалы не
проводят ток и возмущающий сигнал действуя на
образец не вызывает электрохимических реакций.
Частотные зависимости импеданса гетерогенных систем
(ГС) определяются многими физическими причинами,
причем некоторые из них проявляются при одних и тех
же частотах..
76
77.
Основные факторы, влияющие назависимость импеданса Z от частоты ω
1. Электронные релаксационные процессы на границах
раздела фаз. Отличие значений удельной
электропроводности и диэлектрической проницаемости
фаз, составляющих систему, приводит к поляризации
Максвелла–Вагнера, которая характеризуется
определенным временем релаксации, что проявляется в
виде дисперсии импеданса композитных структур.
2. Дисперсия электрических характеристик (удельной
электропроводности и диэлектрической проницаемости)
фаз, входящих в ГС. Например, прыжковая
электропроводность зависит от частоты переменного тока.
Поэтому если в одной из фаз композита (КМ) возможен
прыжковый перенос заряда, то импеданс КМ будет
зависеть от частоты.
77
78.
3. Релаксационные процессы на границах раздела фаз,связанные с переносом ионов и электрохимическими
реакциями. Диффузия и электрохимические реакции
происходят с конечной скоростью, что приводит к
временной зависимости приэлектродных процессов и
появлению частотной дисперсии импеданса.
4. Наличие структурных (имеющих определенную
геометрию) элементов с реактивным импедансом.
Импеданс идеального конденсатора зависит от частоты Z
= 1/(iωC). Поэтому даже в случае отсутствия дисперсии
электрических параметров фаз, составляющих
гетерогенную систему, для образцов с различной
геометрией распределения компонент ГС по ее объему
будут наблюдаться разные частотные зависимости
импеданса.
78
79.
Сложность зависимостей Z(ω) для ГС, с одной стороны,требует тщательного анализа спектров импеданса, с
другой обусловливает большую информативность
импедансной спектроскопии
Выполнение измерений на различных частотах,
построение эквивалентных схем замещения во всем
исследуемом интервале частот и в выделенных
диапазонах, в которых максимально проявляются
одни факторы и минимизированы другие, а также
сравнение эквивалентных схем замещения с
физической моделью гетерогенной системы
позволяет разграничить влияние многочисленных
факторов на Z(ω) и получить необходимую
информацию.
79
80.
Основные элементы импеданснойспектроскопии
Импеданс реального сопротивления
Сопротивление является основным структурным
элементом в импедансных моделях. Сопротивление
обозначается символом R и связывает протекающий
через него ток I с возникающим на нём падением
напряжения UR в виде простого соотношения
UR = RI,
В частотной области
ZR(iω) = R,
т.е. импеданс этого элемента имеет только вещественную
составляющую, которая частотно независима
Re(ZR) = R,
Im(ZR) = 0.
80
81.
Основные элементы импеданснойспектроскопии
Импеданс емкости
Ёмкость – еще один основной модельный элемент. Во
временной области она характеризует соотношение
t
UС (t) = (1/С) ʃ i(t)dt + UC ( t 0 ) ,
t0
где величина ёмкости С является коэффициентом
пропорциональности между напряжением UС и
интегралом тока, протекающего через ёмкость.
В частотной области это соотношение соответствует
зависимости
ZC (jω) = (jωC) -1 = -j(ωC) -1 ,
ZC содержит лишь реактивный компонент,
который для положительных значений С
отрицателен, т.е. изображает отставание
по фазе (задержку) на π/2 (90°).
81
82.
Основные элементы импеданснойспектроскопии
Импеданс индуктивности
Элемент индуктивности L связывает ток с напряжением с
помощью следующего соотношения:
UL ( t ) = L ,
в котором напряжение на элементе L пропорционально
производной тока. В частотной области формула для
импеданса запишется в виде
ZL (jω) = j ω L,
где ZL содержит лишь реактивный компонент, который
положителен для L > 0, т.е. изображает опережение по
фазе на π/2 (90°). С увеличением частоты ZL
пропорционально увеличивается.
82
83.
Представление импеданса иадмиттанса в виде комплексных
чисел
83
84.
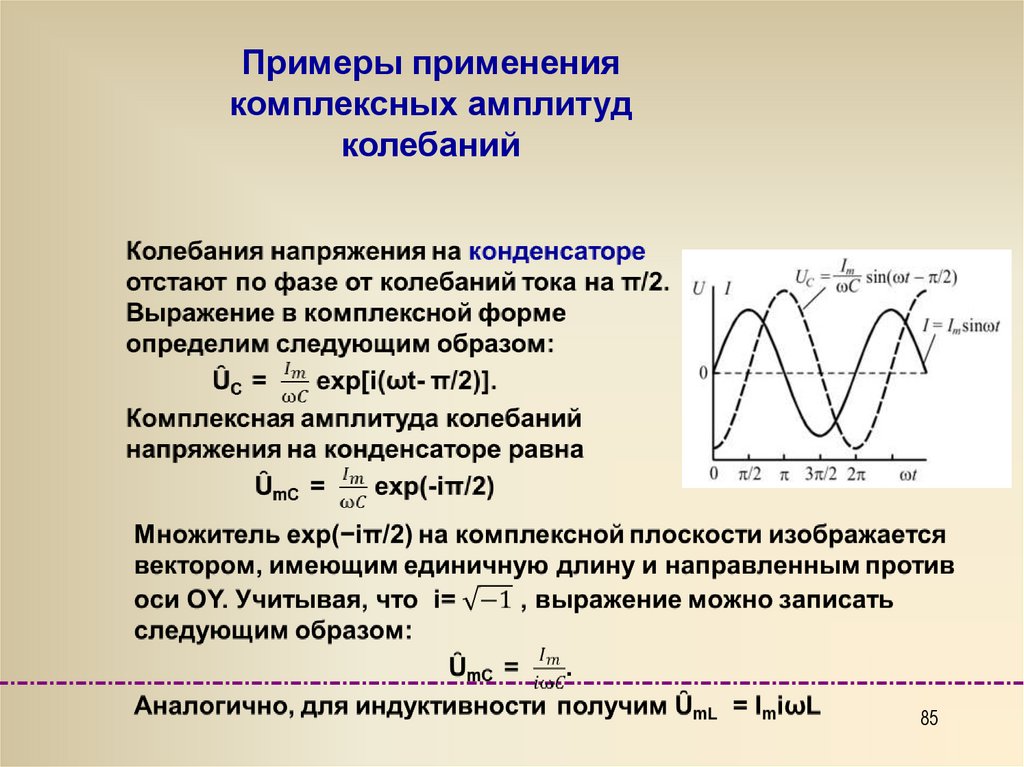
Примеры применениякомплексных амплитуд
колебаний
Комплексные выражения для
колебаний тока на сопротивлении
İ = Im exp( iωt),
и напряжения
ȖR = ImRexp(iωt).
Комплексная амплитуда колебания напряжения
ȖmR= ImRexp(i φ)= ImR
не содержит мнимой части, т. к. при отсутствии сдвига
фаз (φ = 0) между колебаниями тока и напряжения
exp(iφ) = 1.
84
85.
Примеры применениякомплексных амплитуд
колебаний
85
86.
Примеры применениякомплексных амплитуд
колебаний
Комплексные выражения для
колебаний тока
İ = Im exp( iωt),
и напряжения
ȖR = ImRexp(iωt).
на сопротивлении
Комплексная амплитуда колебания напряжения
ȖmR= ImRexp(i φ)= ImR
не содержит мнимой части, т. к. при отсутствии сдвига
фаз (φ = 0) между колебаниями тока и напряжения
exp(i φ) = 1.
86
87.
Примеры применениякомплексных амплитуд
колебаний
Последовательная схема
Для сложения нескольких колебаний одинаковой частоты
достаточно сложить комплексные амплитуды этих колебаний.
Модуль полученного комплексного числа дает фактическую
амплитуду результирующего колебания, а его аргумент
начальную фазу.
87
88.
Примеры применениякомплексных амплитуд
колебаний
88
89.
Примеры применениякомплексных амплитуд
колебаний
Параллельное
соединение
При параллельном соединении складываем токи
Модуль адмиттанса |Y| = Y
представляет собой полную
проводимость цепи
89
90.
Импеданс Варбурга придиффузии полубесконечное
пространство
Этот элемент W введен Варбургом для изображения импеданса идеальной линейной
полубесконечной диффузии, которая во
временной области подчиняется закону
Фика:
дс/дt = D (д2 с/дх2 ).
В частотной области выражение для
соответствующего импеданса будет иметь
вид ZW ( jω ) = λ ( jω ) -1/2 = λω -1/2( l – j ).
Этот импеданс содержит вещественную и
мнимую составляющие, которые равны
между собой и определяют сдвиг по фазе на
π/4 (45°), являющийся частотно
независимым. Модуль импеданса
уменьшается с увеличением частоты. Здесь λ
– коэффициент пропорциональности, и его
можно назвать коэффициентом Варбурга
90
91.
Импеданс Варбурга придиффузии полубесконечное
дс/дt пространство
= D (д2 с/дх2 ).
решение уравнения с учётом
электрохимических параметров приводит к
выражению
ZW ( jω ) = kf ( jωD0 )-1/2 = kf( wD0 )-1/2 (1- j) ,
что позволяет установить соотношение
между параметром λ структурного элемента
W и электрохимическими параметрами
λ = kf D0-1/2,
где кf – константа скорости окислительной реакции, которая
протекает на электродной поверхности, a D0 - коэффициент
диффузии частиц окисляемого вещества.
При протекании окислительно-восстановительной реакции
импеданс определяется константами скорости как окисления kf,
так и восстановления kb, а также коэффициентами диффузии D0 и
DR.
В этом случае λ = kf D0-1/2 + kbDR-1/2 .
91
92.
Импеданс Варбурга придиффузии в ограниченное
пространство
Этот элемент моделирует
импеданс
линейного диффузионного процесса,
протекающего в однородном слое с конечной
толщиной. Обознается как BW.
Решение этой задачи, имеет следующий вид:
ZBW ( jω ) = R Ct k f ( jωD0 ) -1/2 th ( jωδ2N/D0)1/2,
где RCt – сопротивление переноса заряда;
kf - константа скорости окисления
DО – коэффициент диффузии частиц окисляемого вещества;
δN – толщина диффузионного слоя Нернста.
Конечный диффузионный импеданс имеет интересные свойства.
При ω→∞ импеданс элемента BW стремится к импедансу Варбурга
ZW. То же соотношение справедливо и для δN → ∞, причем ZBW по
определению переходит в диффузионный импеданс для
полубесконечной диффузии.
92
93.
Импеданс Варбурга придиффузии в ограниченное
пространство
При высоких частотах
диаграмма хорошо
аппроксимируется линейной диаграммой
импеданса Варбурга. С уменьшением
частоты диаграмма описывает небольшой
“горб" над линией W, после чего плавно,
почти по траектории полуокружности,
снижается до предельного значения
lim ZBW ( jω ) = RCt kfδND0-1
ω→0
Эта траектория образует с вещественной осью определённый
угол, равный π/2 (90°).
Для импеданса элемента BW имеют место также эмпирические
формулы h ≈ 0,42 RCt kfδND0-1 , a ≈ 0,58 RCt kfδND0-1 ,
где a и h - координаты максимума мнимого компонента.
Структурная модель импеданса элемента ВW имеет вид
ZBW ( jω ) = λ ( jω ) -1/2 th ( jωR20/λ )1/2 .
93
94.
Импеданс Варбурга придиффузии в ограниченное
пространство
Структурная модель импеданса элемента
ВW имеет вид
ZBW ( jω ) = λ ( jω ) -1/2 th( jωR20/λ )1/2 .
Учитывая
ZBW ( jω ) = R Ct k f ( jωD0 )-1/2 th( jωδ2N/D0)1/2
Получим
λ = Rct kf D0-1/2 ; R0 = Rct kf δND0-1.
Следует подчеркнуть, что из анализа импедансной диаграммы
можно определить только модельные параметры λ и R0.
94
95.
Элемент с постояннымсдвигом фаз (СРЕ)
Экспериментально наблюдаемые частотные
зависимости проводимостей редко
описываются выражением, где показатель
степени равен строго 1.0 для емкости, строго
0,5 для диффузии.
Поэтому был введен некоторый обобщенный
элемент, проводимость которого описывается
выражением
Y = A (iω)n.
Импеданс элемента с постоянной фазой можно выразить как
ZСРЕ = A-1( jω )-n ,
где А - фактор пропорциональности; n – экспоненциальный
показатель, обозначающий фазовое отклонение.
95
96.
Элемент с постояннымсдвигом фаз (СРЕ)
Для целых значений n = 1, 0, -1 элемент СРЕ
вырождается до классических элементов с
сосредоточенными параметрами С, R и L. Для
n = 0,5 СРЕ дает импеданс Варбурга в чистом
виде.
Для n = 1 – ε, где 0 ≤ ε < ( 0,1 + 0,2 ) (область С)
СРЕ даёт импеданс чистого или
распределённого ёмкостного элемента.
Для n = 0,5 ± ε (область импеданса Варбурга W), СРЕ моделирует
импеданс идеальной или деформированной диффузии.
Для n = 0 ± ε (область R) СРЕ описывает импеданс чистого или
распределённого (искажённого) резистивного элемента.
Для n = -1 + ε (область L) СРE моделирует импедансное поведение
чистого или искажённого индуктивного элемента.
96
97.
Элемент с постояннымсдвигом фаз (СРЕ)
Коэффициент А имеет формальное значение фактора
пропорциональности, однако для целых или дробных значений n
А приобретает определённый физический смысл и размерность
ёмкости (С), коэффициента Варбурга (λ), сопротивления (R) и
индуктивности (L). При варьировании значений n необходимо
изменять размерность фактора А, а из этого следует и изменение
физической природы А в зависимости от n.
97
98.
Импедансы основныхэлементов
ZR = R
ZC = 1/(iωC) = -i/(ωC)
ZL = iωL
ZW = (1-i)Wω-1/2
ZCPE = A-1( iω )-n
98
99.
Вторая часть нашего введения вимпедансную спектроскопию
Слайд 99
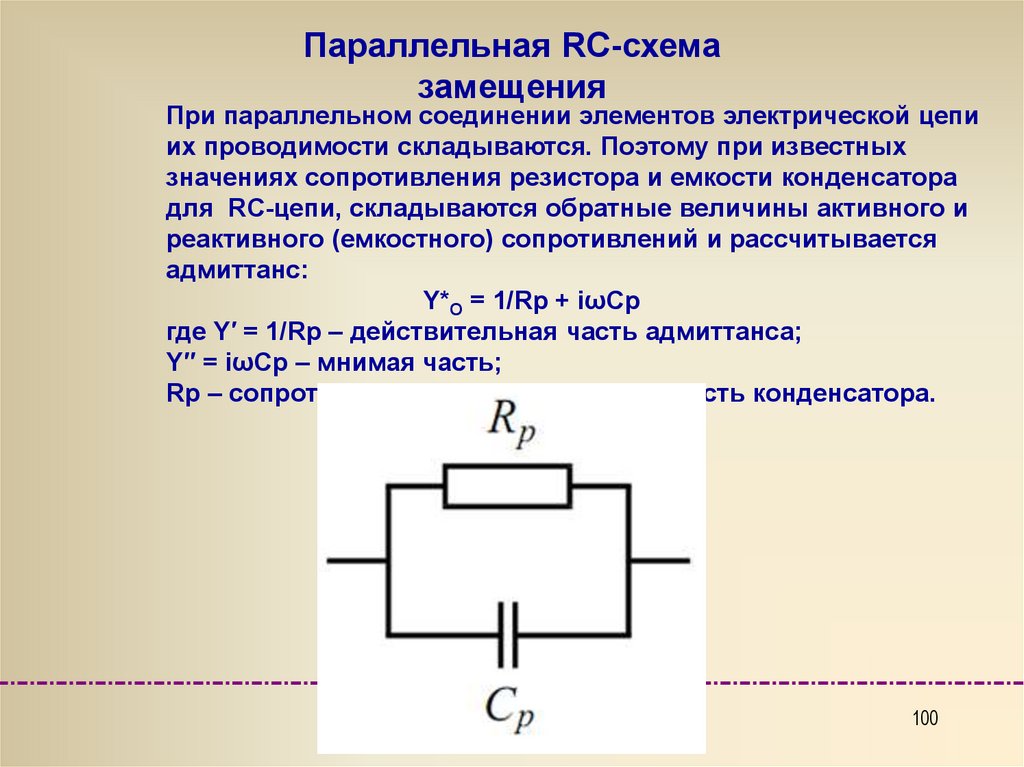
100.
Параллельная RC-схемазамещения
При параллельном соединении элементов электрической цепи
их проводимости складываются. Поэтому при известных
значениях сопротивления резистора и емкости конденсатора
для RC-цепи, складываются обратные величины активного и
реактивного (емкостного) сопротивлений и рассчитывается
адмиттанс:
Y*O = 1/Rp + iωCp
где Y′ = 1/Rp – действительная часть адмиттанса;
Y′′ = iωCp – мнимая часть;
Rp – сопротивление резистора; Cp – емкость конденсатора.
100
101.
Параллельная RC-схемазамещения
Откладывая в комплексной плоскости значения
действительной и мнимой частей Y* для каждой частоты,
можно построить годограф адмиттанса.
Он представляет собой параллельный оси Y′′ луч,
выходящий из точки 1/Rp на оси Y′.
Импеданс Z* параллельной RC-цепи вычисляют как
величину, обратную адмиттансу Y*:
101
102.
Параллельная RC-схемазамещения и мнимую части:
Разделяем действительную
после умножения обеих частей
на Z′ принимает вид
102
103.
Параллельная RC-схемазамещения
Радиус равен Rp/2, а центр расположен на оси Z′ на
расстоянии Rp/2 от начала координат.
Если частота переменного тока ω увеличивается (в
пределе ω →∞), то импеданс параллельной RC-цепи
стремится к нулю, т.е. конденсатор шунтирует резистор.
При нулевой частоте импеданс конденсатора бесконечно
велик, весь ток протекает через резистор и,
соответственно, Z ≈ Z′ ≈ Rp.
103
104.
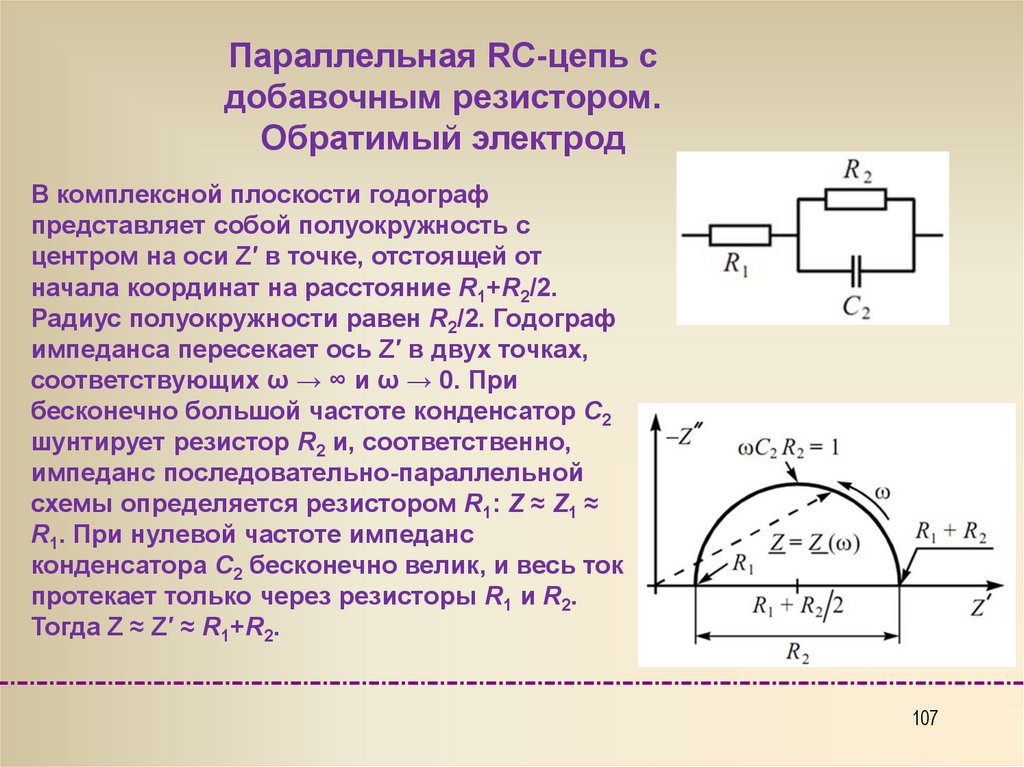
Параллельная RC-цепь сдобавочным резистором.
Обратимый электрод
Параллельная R2C2-цепь с добавочным сопротивлением R1
применяется для описания поведения поляризуемого
(обратимого) электрода, когда на его поверхности протекает
одностадийная электрохимическая реакция и отсутствуют
любые диффузионные ограничения. Структурные параметры
имеют прямой физический смысл:
R1 – сопротивление электролита,
R2 – сопротивление переноса заряда,
C2 – емкость двойного электрического слоя.
104
105.
Параллельная RC-цепь сдобавочным резистором.
Обратимый электрод
105
106.
Параллельная RC-цепь сдобавочным резистором.
Обратимый электрод
Последние три слагаемые в представляют
собой квадрат суммы.
106
107.
Параллельная RC-цепь сдобавочным резистором.
Обратимый электрод
В комплексной плоскости годограф
представляет собой полуокружность с
центром на оси Z′ в точке, отстоящей от
начала координат на расстояние R1+R2/2.
Радиус полуокружности равен R2/2. Годограф
импеданса пересекает ось Z′ в двух точках,
соответствующих ω → ∞ и ω → 0. При
бесконечно большой частоте конденсатор C2
шунтирует резистор R2 и, соответственно,
импеданс последовательно-параллельной
схемы определяется резистором R1: Z ≈ Z1 ≈
R1. При нулевой частоте импеданс
конденсатора C2 бесконечно велик, и весь ток
протекает только через резисторы R1 и R2.
Тогда Z ≈ Z′ ≈ R1+R2.
107
108.
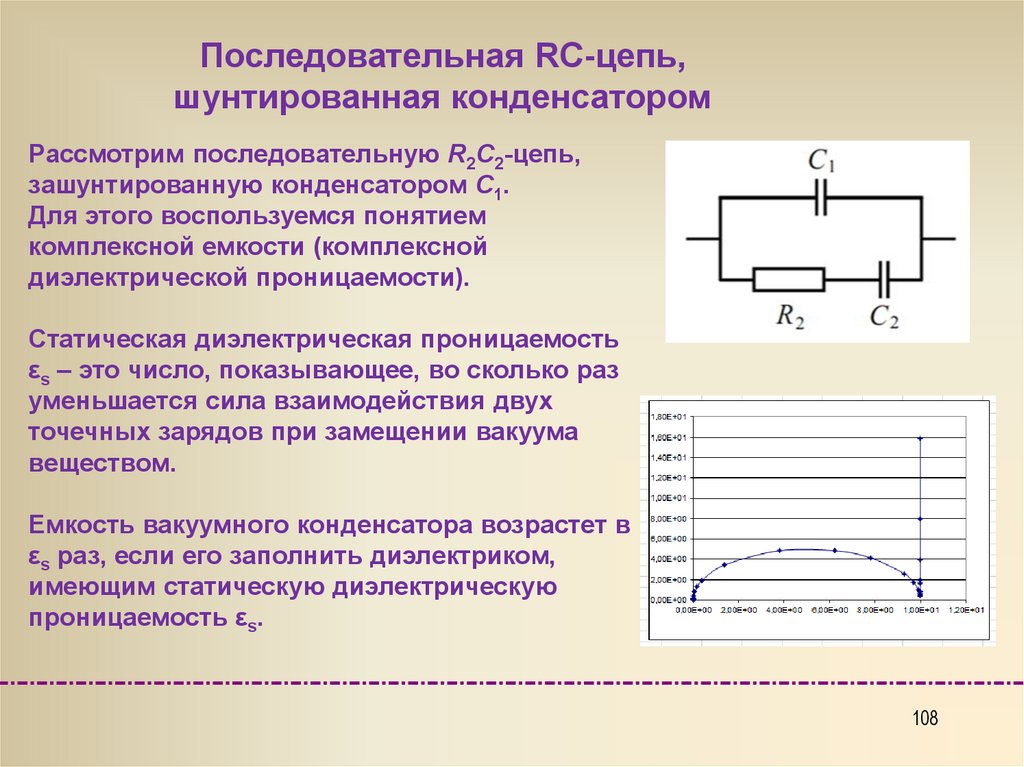
Последовательная RC-цепь,шунтированная конденсатором
Рассмотрим последовательную R2C2-цепь,
зашунтированную конденсатором С1.
Для этого воспользуемся понятием
комплексной емкости (комплексной
диэлектрической проницаемости).
Статическая диэлектрическая проницаемость
εs – это число, показывающее, во сколько раз
уменьшается сила взаимодействия двух
точечных зарядов при замещении вакуума
веществом.
Емкость вакуумного конденсатора возрастет в
εs раз, если его заполнить диэлектриком,
имеющим статическую диэлектрическую
проницаемость εs.
108
109.
Последовательная RC-цепь,шунтированная конденсатором
Комплексная диэлектрическая проницаемость ε*= ε′ − iε′′ учитывает
относительную диэлектрическую проницаемость диэлектрика
(действительная часть – ε′), а также потери, связанные с
переполяризацией и сквозной проводимостью (мнимая часть – ε′′).
Комплексная емкость и комплексная диэлектрическая
проницаемость связаны соотношением
где С0 – емкость конденсатора, имеющего те же
геометрические размеры, что и исследуемый, но не
заполненного веществом (вакуумного конденсатора).
109
110.
Последовательная RC-цепь,шунтированная конденсатором
Воспользовавшись тем, что C* = Y*/iω, перейдем от
комплексной проводимости (адмиттанса) к комплексной
емкости C* и выделим при этом действительную C′ и
мнимую C′′ части C*:
110
111.
Последовательная RC-цепь,шунтированная конденсатором
111
112.
Последовательная RC-цепь,шунтированная конденсатором
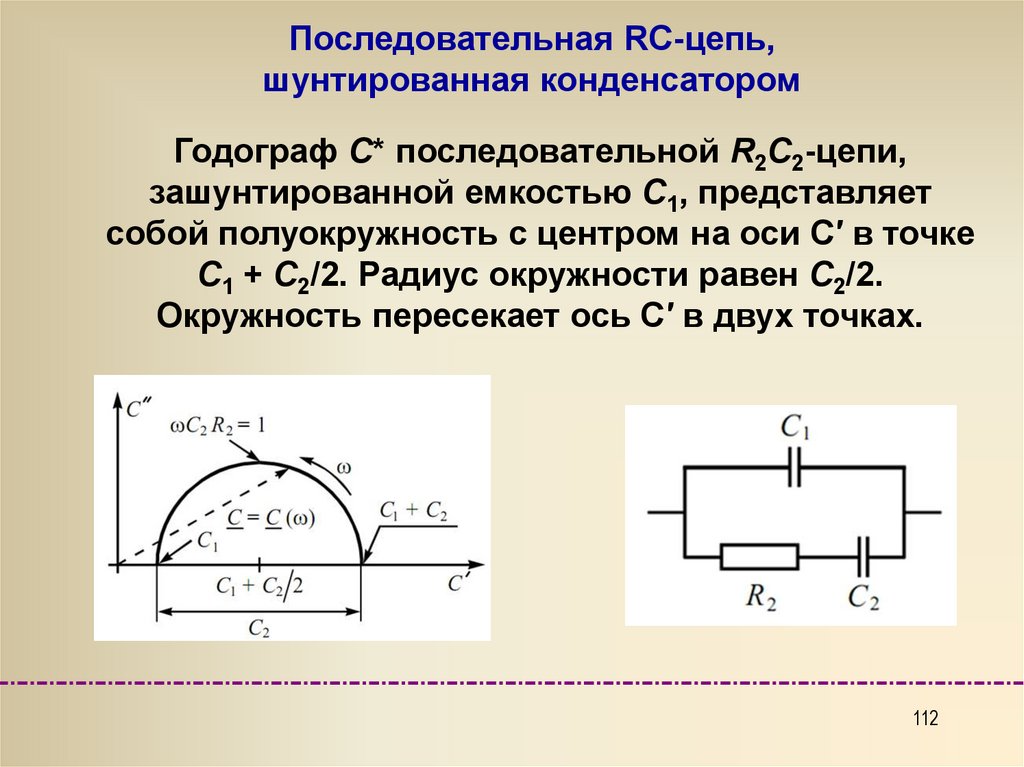
Годограф C* последовательной R2C2-цепи,
зашунтированной емкостью C1, представляет
собой полуокружность с центром на оси C′ в точке
C1 + C2/2. Радиус окружности равен C2/2.
Окружность пересекает ось C′ в двух точках.
112
113.
Последовательная RC-цепь,шунтированная конденсатором
При малой частоте емкость цепи
представляет собой сумму емкостей
двух конденсаторов C1 + C2.
при ω → ∞ емкость определяется
конденсатором C1, что соответствует
пересечению годографа комплексной
емкости с осью C′ в точке C1.
113
114.
Последовательная RC-цепь,шунтированная сопротивлением
Сократив правую часть на 1/Y′′2, получим:
114
115.
Последовательная RC-цепь,шунтированная сопротивлением
Разделив левую и правую часть на
Y′ − 1/R1 и перенеся все члены в
левую часть, можно получить
уравнение годографа
115
116.
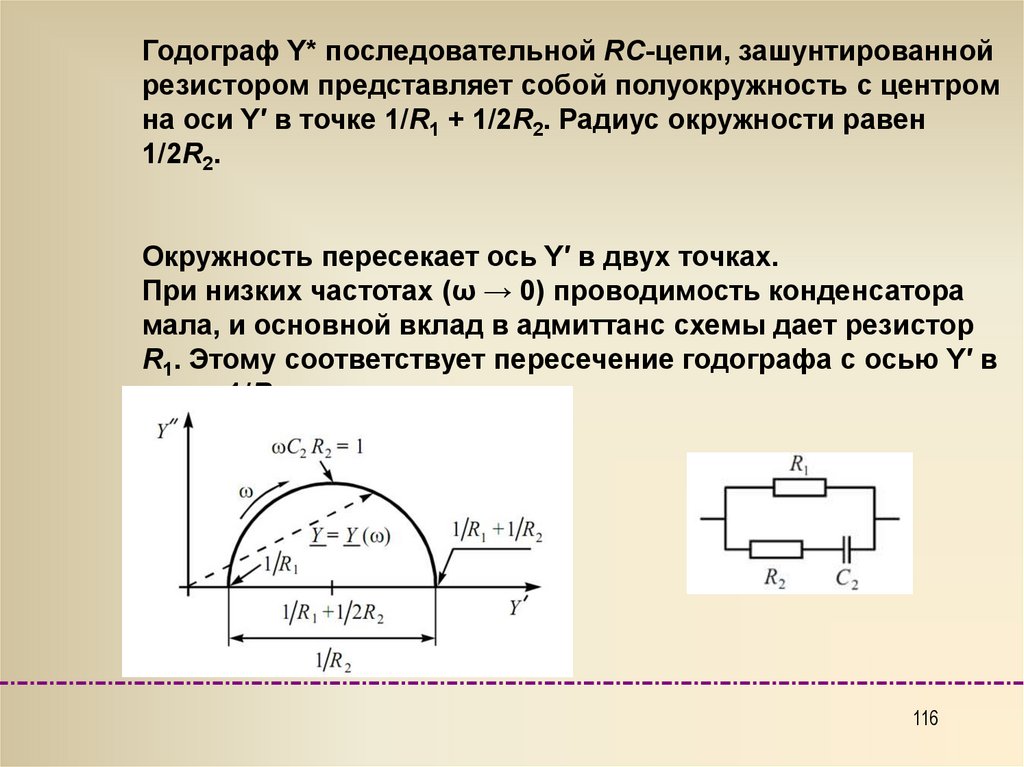
Годограф Y* последовательной RC-цепи, зашунтированнойрезистором представляет собой полуокружность с центром
на оси Y′ в точке 1/R1 + 1/2R2. Радиус окружности равен
1/2R2.
Окружность пересекает ось Y′ в двух точках.
При низких частотах (ω → 0) проводимость конденсатора
мала, и основной вклад в адмиттанс схемы дает резистор
R1. Этому соответствует пересечение годографа с осью Y′ в
точке 1/R1.
116
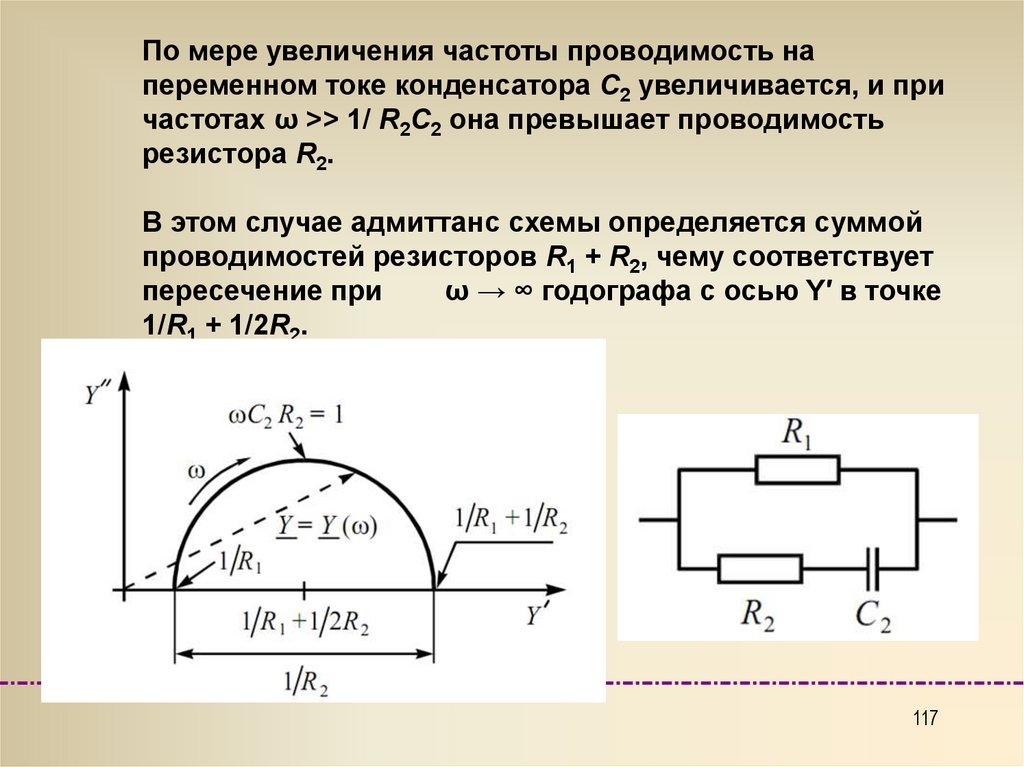
117.
По мере увеличения частоты проводимость напеременном токе конденсатора C2 увеличивается, и при
частотах ω >> 1/ R2C2 она превышает проводимость
резистора R2.
В этом случае адмиттанс схемы определяется суммой
проводимостей резисторов R1 + R2, чему соответствует
пересечение при
ω → ∞ годографа с осью Y′ в точке
1/R1 + 1/2R2.
117
118.
Параллельная RC-цепь сдобавочным конденсатором
118
119.
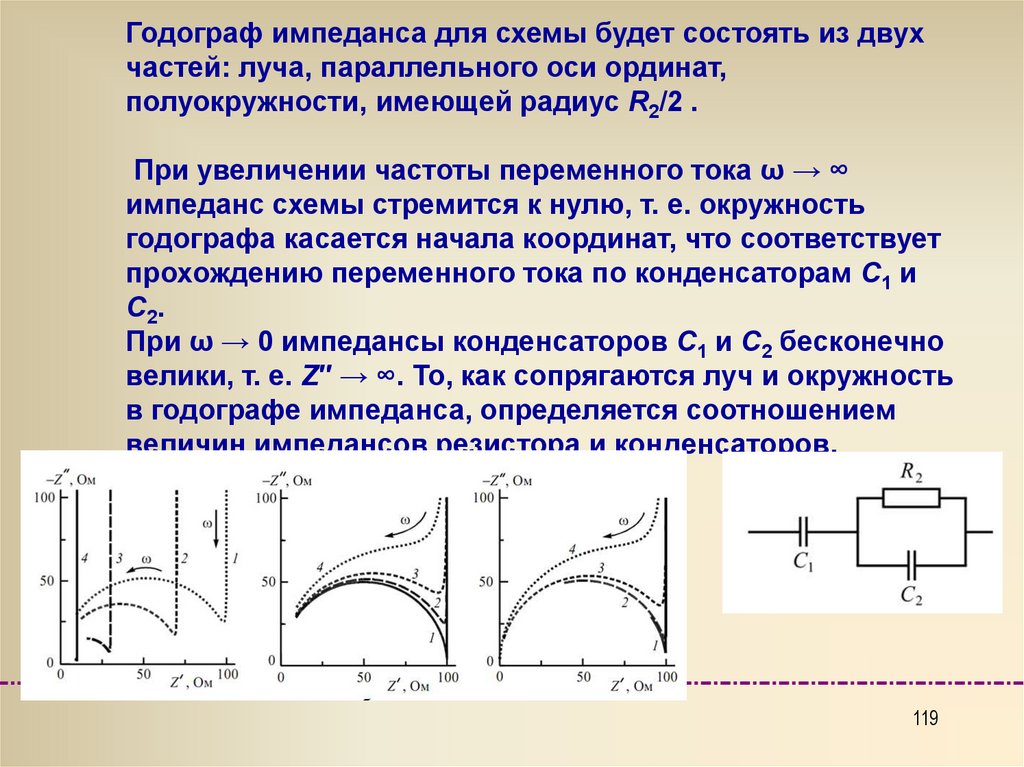
Годограф импеданса для схемы будет состоять из двухчастей: луча, параллельного оси ординат,
полуокружности, имеющей радиус R2/2 .
При увеличении частоты переменного тока ω → ∞
импеданс схемы стремится к нулю, т. е. окружность
годографа касается начала координат, что соответствует
прохождению переменного тока по конденсаторам С1 и
C 2.
При ω → 0 импедансы конденсаторов С1 и C2 бесконечно
велики, т. е. Z′′ → ∞. То, как сопрягаются луч и окружность
в годографе импеданса, определяется соотношением
величин импедансов резистора и конденсаторов.
119
120.
120121.
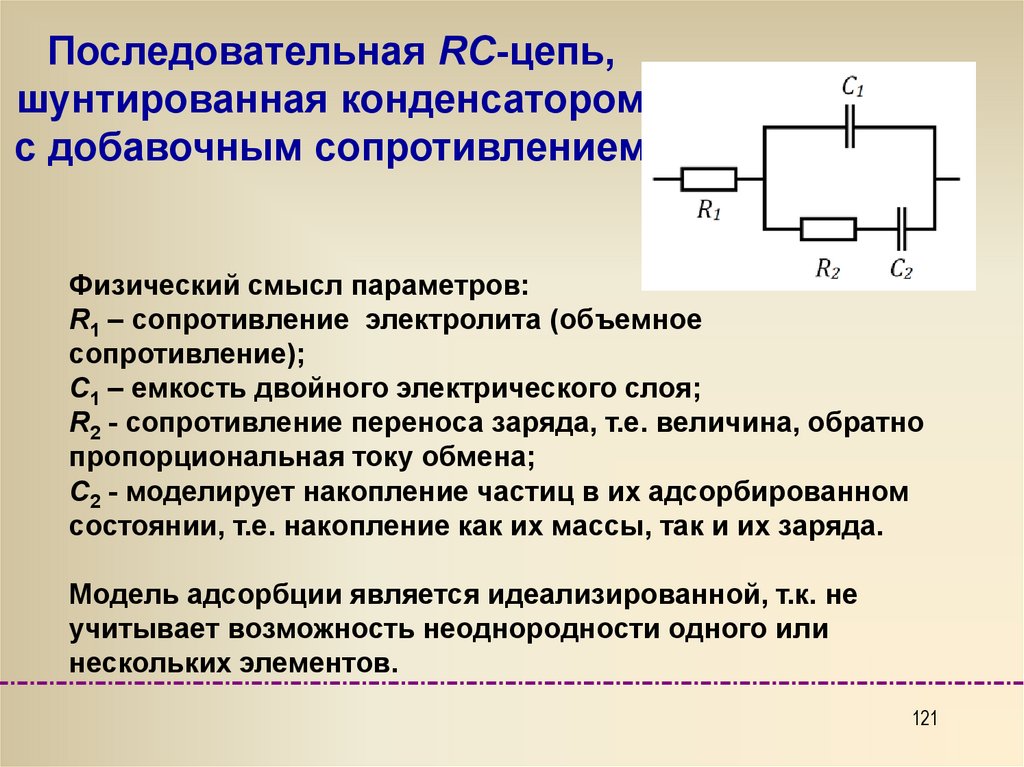
Последовательная RC-цепь,шунтированная конденсатором
с добавочным сопротивлением
Физический смысл параметров:
R1 – сопротивление электролита (объемное
сопротивление);
С1 – емкость двойного электрического слоя;
R2 - сопротивление переноса заряда, т.е. величина, обратно
пропорциональная току обмена;
С2 - моделирует накопление частиц в их адсорбированном
состоянии, т.е. накопление как их массы, так и их заряда.
Модель адсорбции является идеализированной, т.к. не
учитывает возможность неоднородности одного или
нескольких элементов.
121
122.
Последовательная RCW-цепь,шунтированная конденсатором и
Фарадеевским сопротивлением и с
добавочным сопротивлением
Сопротивление R1 - объемное сопротивление твердого
электролита, С1 – емкость двойного электрического слоя;
R2 моделирует сопротивление перехода частиц из
двойного слоя в адсорбированное состояние, С2 –
адсорбционную емкость, W2 – диффузионные ограничения
или импеданс Варбурга, RF1 – фарадеевское
сопротивление или сопротивление переноса заряда.
122
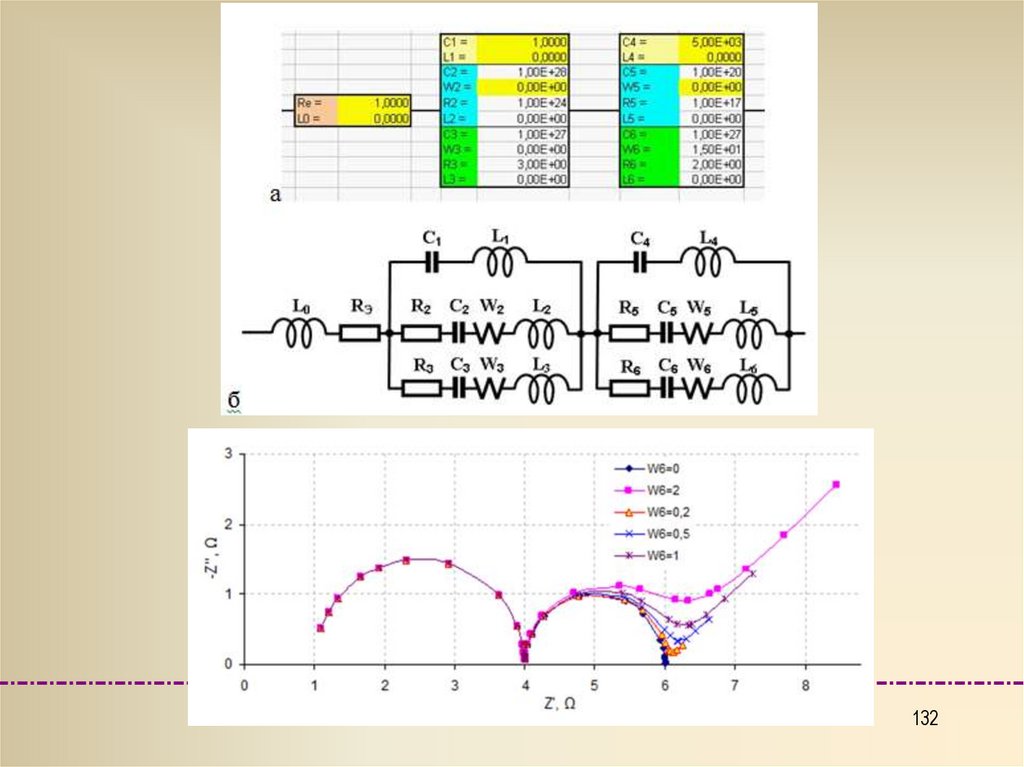
Эквивалентная схема для обратимого электрода
123.
Графоаналитический метод определенияпараметров эквивалентных схем.
Электродный импеданс и объемное
сопротивление электролита
Простейшим методическим приемом определения
эквивалентной схемы замещения является
последовательное применение различных
представлений эквивалентной схемы.
На каждом этапе анализа рассматривают простейшую
(например, двухэлементную резистор и конденсатор)
схему замещения.
Определив численное значение емкости или
сопротивления какого-либо из элементов, его исключают
из общего измеренного импеданса (адмиттанса и т. д.) и
затем преобразуют остаток в следующую схему
(представление).
Так поступают до тех пор, пока не будут выяснены все
параметры многокомпонентной эквивалентной схемы
замещения.
123
124.
Графоаналитический метод определенияпараметров эквивалентных схем.
Электродный импеданс и объемное
сопротивление электролита
В экспериментальных исследованиях мы имеем дело с
объектами, которым присущи все три вида сопротивления –
активное, емкостное и индуктивное.
Измеряемый импеданс
Измеренные последовательные емкость Cs и
резистор Rи, после внесения поправки на
импеданс проводов, откладываются в
координатах Rи, Xs=( Cs)-1
124
125.
Графоаналитический метод определения параметровэквивалентных схем. Электродный импеданс и объемное
сопротивление электролита
Определенную величину Rэ вычитаем из общего
сопротивления Rи и остаток Rs = Rи – Rэ и Cs приводим к
параллельной RC схеме с помощью соотношений
После этого строили графики Ср, 1/ Rp и (Сp-C1),
1/Rp. Производя экстраполяцию соответственно на
бесконечно большую и нулевую частоты находили
емкость двойного слоя Сd и сопротивление
переноса заряда RF.
125
126.
Графоаналитический метод определения параметровэквивалентных схем. Электродный импеданс и
объемное сопротивление электролита
Остаточные значения Ср – Cd и Rp-1-RF-1 снова приводили
к последовательной схеме и по соотношениям:
Строим графики
зависимостей
126
127.
Графоаналитический метод определения параметровэквивалентных схем. Электродный импеданс и объемное
сопротивление электролита
Для достижения большей точности используют метод итерации - исходя
из критерия линейной зависимости CФ-1~










































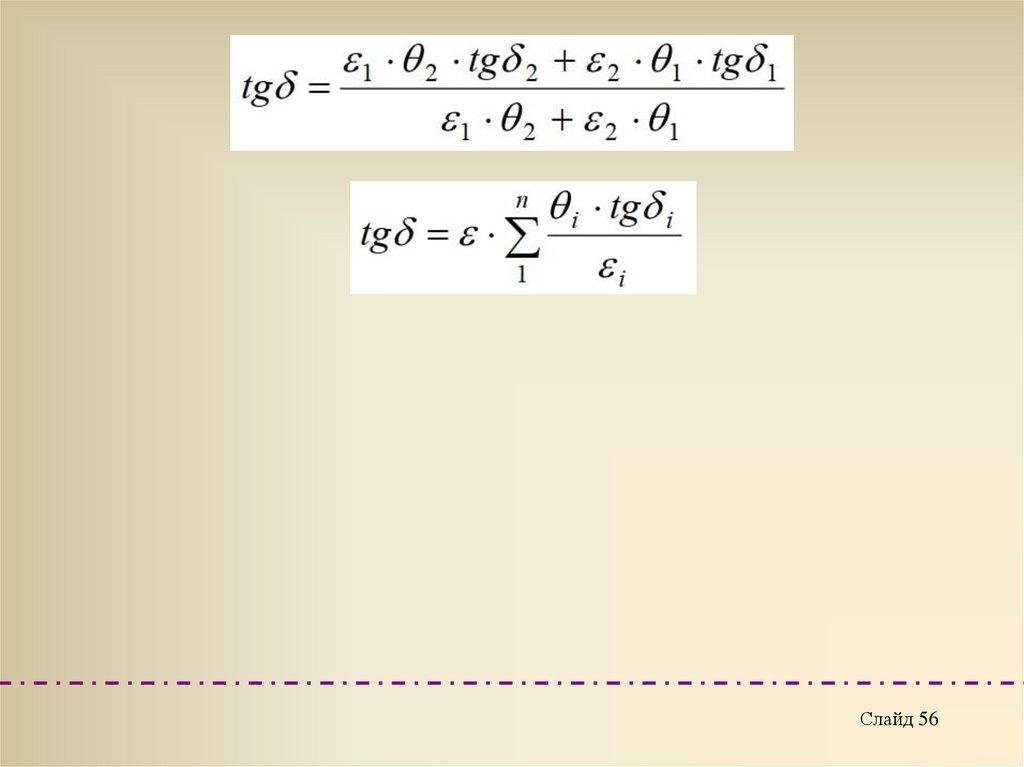





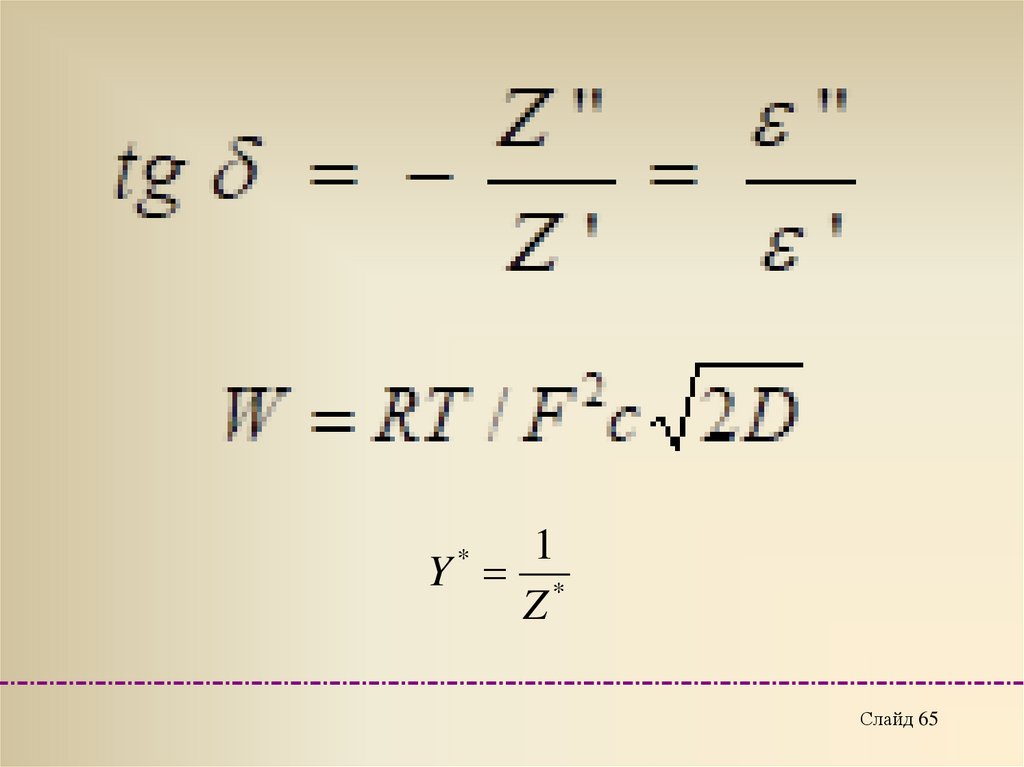
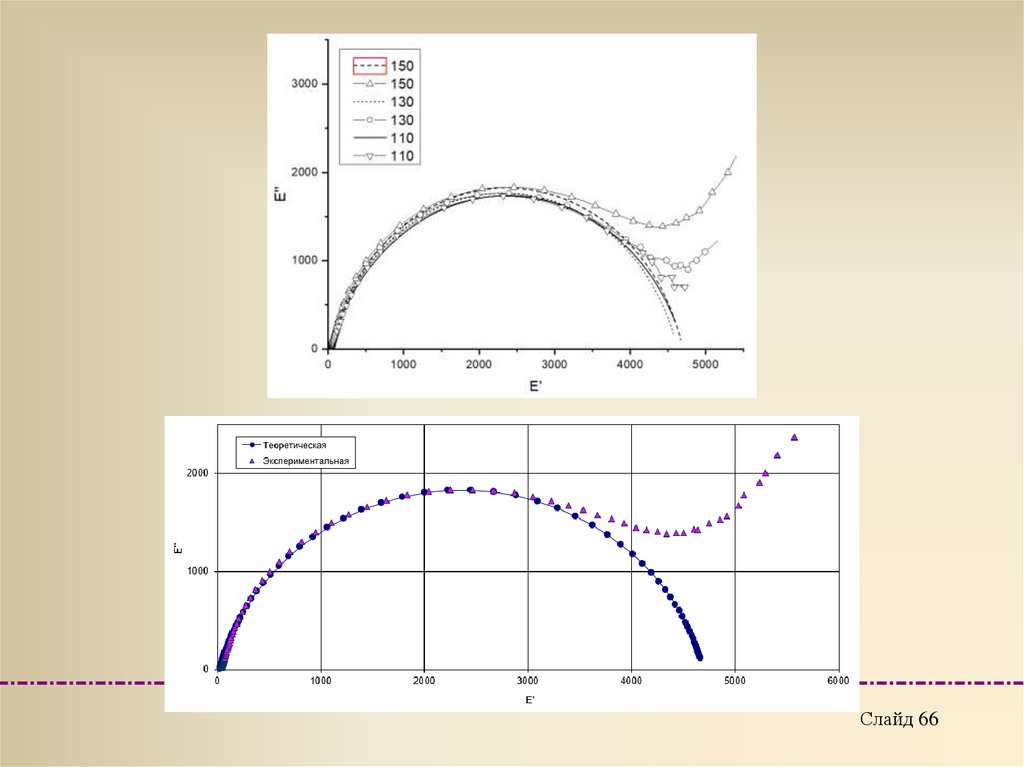
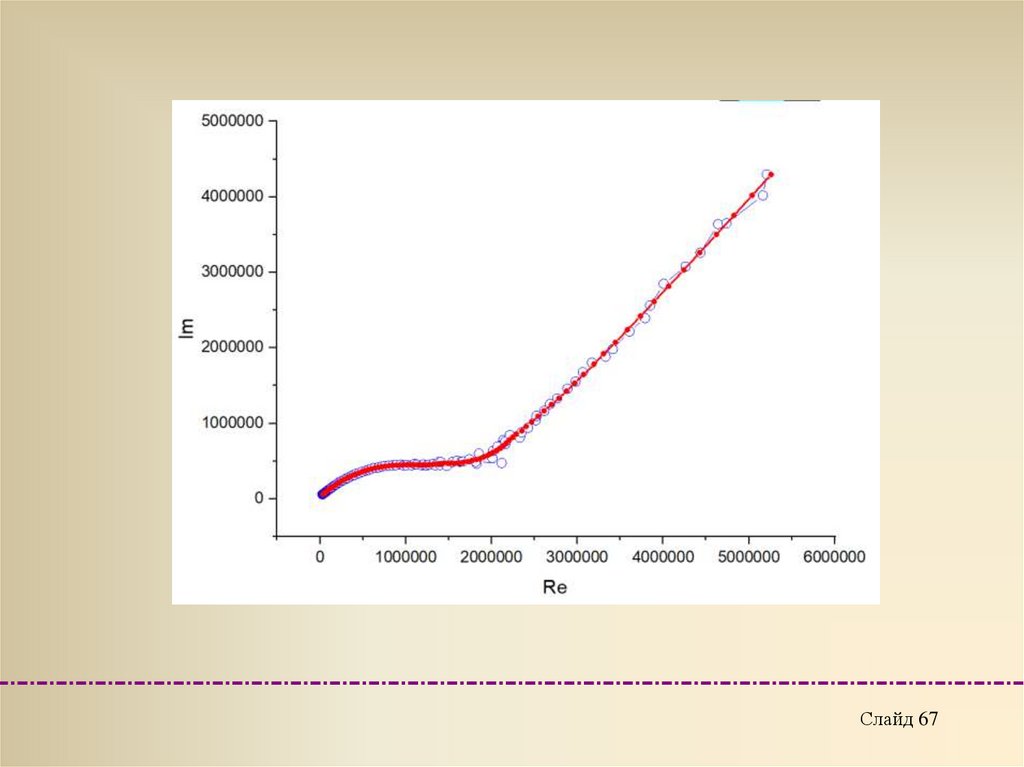
















































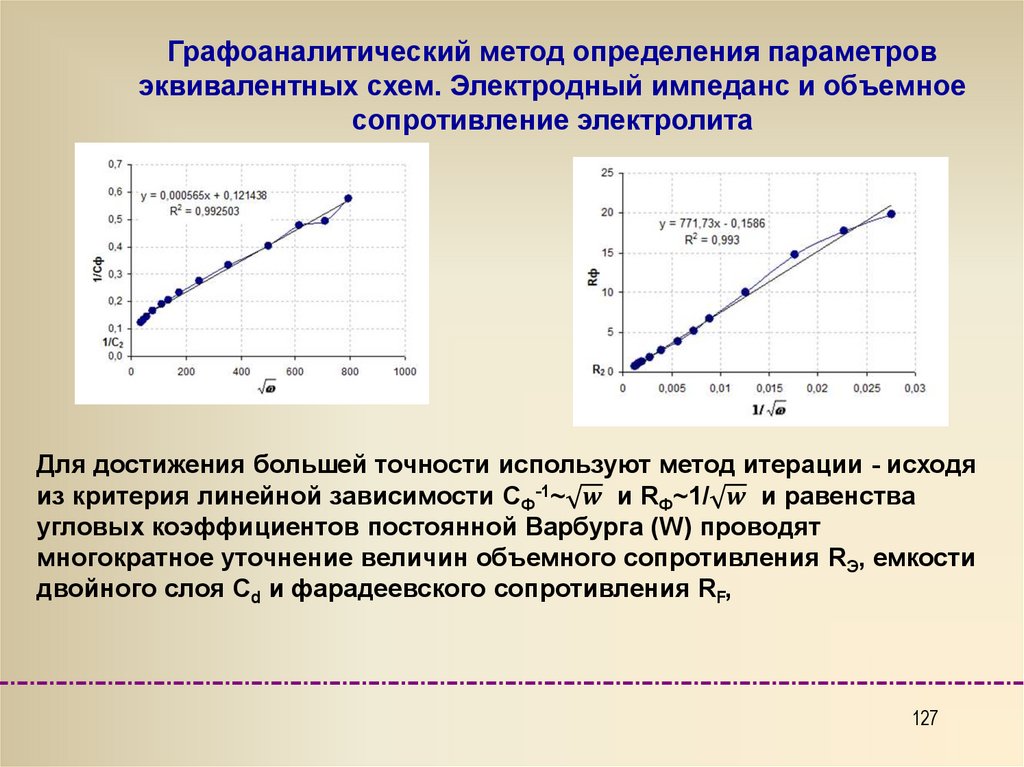


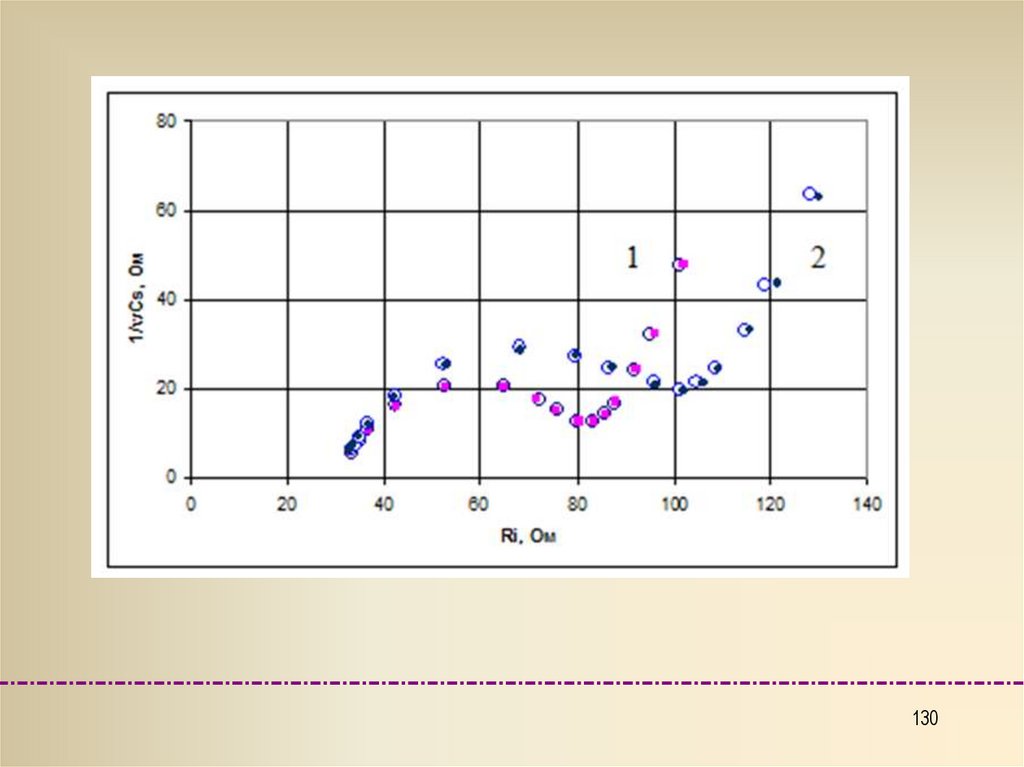

 physics
physics








