National Research University "Higher School of Economics"

1.

National Research University "Higher
School of Economics"
The Moscow Institute of Electronics
and Mathematics
Author: Karapetyan Andrey
Varuzhanovich
Scientific supervisor:
Andrey Yuryevich Gorchakov
Associate Professor
Development of Methods for
Assessing the Level of Confidence in
a Machine Learning Model. Using the
Example of the K-Nearest Neighbors
Method
Moscow,
Russia
2024

2.

2
Contents
1. Relevance and Novelty
2. Goals
3. Objectives
4. Methods
5. Current Results
6. Anticipated Results
7. References

3.

HSE Tikhonov Moscow Institute of
Electronics and Mathematics
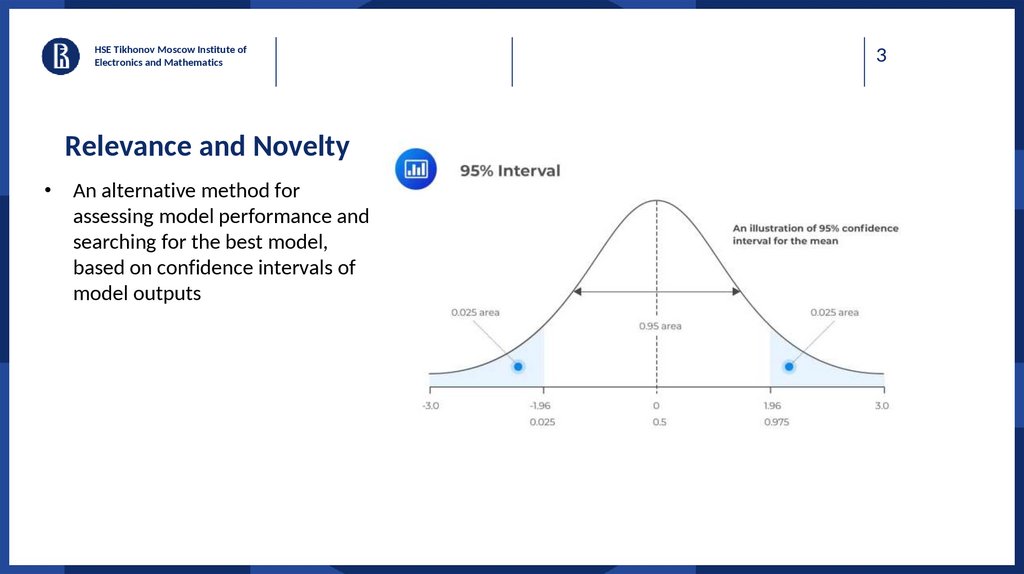
Relevance and Novelty
• An alternative method for
assessing model performance and
searching for the best model,
based on confidence intervals of
model outputs
3

4.

HSE Tikhonov Moscow Institute of
Electronics and Mathematics
Goals
Investigate the feasibility of utilizing
confidence intervals of model predictions
to assess its confidence and performance
for each sample object
Usage of the obtained confidence
intervals in model stacking i.e. for each
object, those models that are most
confident in their predictions for those
specific objects are used
4

5.

5
HSE Tikhonov Moscow Institute of
Electronics and Mathematics
Objectives
Researching the effectiveness of the method on one-dimensional and two-dimensional problems.
Generalization to the multidimensional case
Evaluating the method's performance on public datasets
Comparative analysis

6.

6
Methods
Data is sourced from the internet or generated by computer algorithms, then divided into training and
testing sets
Model training. Model is bagging with k-NN as base models
Assessing model confidence in predictions for each object in the testing part by calculating confidence
intervals using bootstrap resampling of the responses from the base algorithms
Stacking and comparing on test with Random Search and Grid Search using metrics such as MAE and
MSE

7.

7
HSE Tikhonov Moscow Institute of
Electronics and Mathematics
Current results
Fig.
1. Graph
of prediction
intervals.
The model
intervals
are5
marked
in isorange,
andpoints
predictions
of the
with
neighbors
used.
The
represent
the
objects
of the
dataset

8.

8
HSE Tikhonov Moscow Institute of
Electronics and Mathematics
Current results
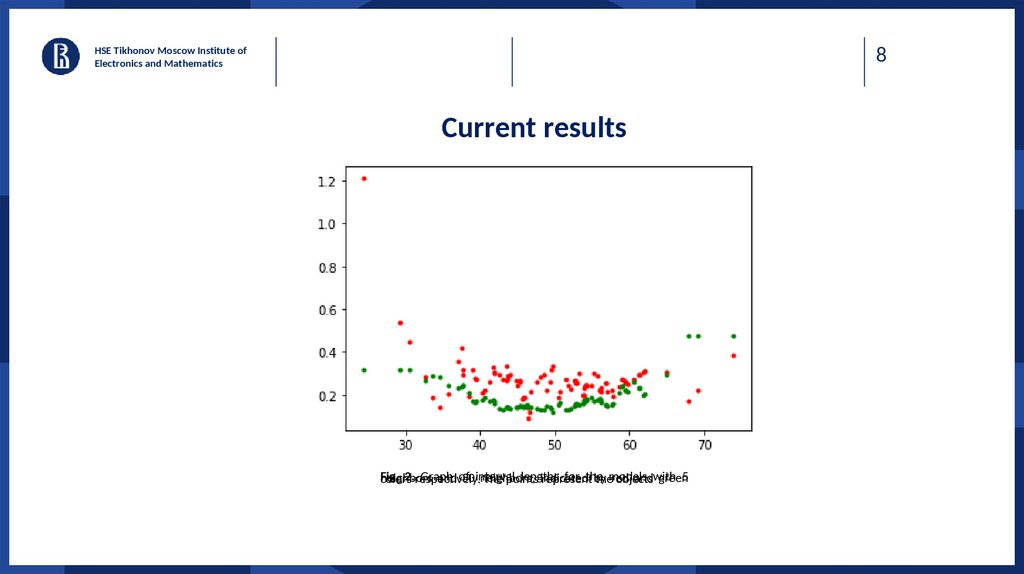
Fig.
2.respectively.
Graph
lengths
for the
5
neighbors
and of
50interval
neighbors,
indicated
by
red
andwith
green
colors
The points
represent
themodels
objects

9.

9
HSE Tikhonov Moscow Institute of
Electronics and Mathematics
Anticipated Results
• Method performance across different tasks
• Program code with calculations
• Results interpretation

10.

10
HSE Tikhonov Moscow Institute of
Electronics and Mathematics
References
Hastie, T, Tibshirani, R., Friedman, J. The Elements of Statistical Learning. Springer, 2001. p. 18. ISBN 0-387-95284-5.
Kohavi R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection // 14th International Joint Conference on Artificial Intelligence,
Palais de Congres Montreal, Quebec, Canada, 1995.
Steven Yu. Stacking and Blending — An Intuitive Explanation.https://medium.com/@stevenyu530_73989/stacking-and-blending-intuitive-explanation-of-advancedensemble-methods-46b295da413c. Accessed January 8, 2024.
Efron, B., Tibshirani, R. An Introduction to the Bootstrap. Boca Raton, FL: Chapman & Hall/CRC, 1993. ISBN 0-412-04231-2.
Dekking F.M., Kraaikamp, Cornelis, Lopuhaä H. P., Meester L. E. "A Modern Introduction to Probability and Statistics". Springer Texts in Statistics, 2005. ISBN 978-185233-896-1. ISSN 1431-875X.
Hamed M.G, Serrurier M., Durand N. Simultaneous Interval Regression for K-Nearest Neighbor. AI 2012: Advances in Artificial Intelligence. AI 2012. Lecture Notes in
Computer Science, V. 7691. Springer, Berlin, Heidelberg, 2012. ISBN 978-3-642-35100-6
Hamed M.G., Serrurier M., Durand N. Possibilistic KNN Regression Using Tolerance Intervals. Advances in Computational Intelligence. IPMU 2012. Communications in
Computer and Information Science, V. 299. Springer, Berlin, Heidelberg, 2012. ISBN 978-3-642-31717-0
A. K. Jain, R. C. Dubes, C. -C. Chen. Bootstrap Techniques for Error Estimation. IEEE Transactions on Pattern Analysis and Machine Intelligence V. PAMI-9, N. 5, 1987,
pp. 628-633.
Aslam, Javed A., Popa, Raluca A. and Rivest, Ronald L. On Estimating the Size and Confidence of a Statistical Audit, Proceedings of the Electronic Voting Technology
Workshop (EVT '07), Boston, MA, August 6, 2007.
Evelyn F., Hodges, J. L. Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties. USAF School of Aviation Medicine, Randolph Field, Texas, 1951.
Beyer K. et al. "When is "nearest neighbor" meaningful?". Database Theory—ICDT'99, 1999, pp. 217–235.
Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, 2011, pp. 2825-2830.
Virtanen P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python // Nature methods, 2020, t. 17, ch. 3, pp. 261-272.