Механические колебания и волны. Затухающие колебания

1.

Физика 1 курс, 2 семестр
Специалитет
Лекция 7. Механические колебания
и волны
- Затухающие колебания
- Вынужденные колебания
В.И. Читайкин
кандидат физико-математических наук
доцент

2.

План лекции
Наименование раздела
Номер
слайда
Введение
3
Раздел 1. Затухающие колебания
4
1.1. Определение, основные характеристики
5
1.2. Дифференциальное уравнение затухающих колебаний
6
1.3. «Канонический» вид уравнения затухающих колебаний и график
7
1.4. Параметры затухающих колебаний
8
Раздел 2. Вынужденные колебания
9
2.1. Определение. Дифференциальное уравнение вынужденных колебаний
10
2.2. Решение уравнения вынужденных колебаний. График
11
2.3. Резонанс
12
2

3.

Введение
В предыдущей, 6-ой лекции были рассмотрены кинетика и динамика механических
гармонических колебаний в общей постановке. Напомню: при гармонических колебаниях все
основные параметры (перемещение, скорость, ускорение и сила) изменяются во времени строго
как cos(ω∙t + α0) или как sin(ω∙t + α0+π/2).
В 7-ой лекции даются понятия затухающих (раздел 1) и вынужденных (раздел 2) колебаний
как особых видов колебательного движения, но, тем не менее, остающихся гармоническими.
Такие колебания более полно соответствуют реальным колебательным процессам, нежели
строго гармонические, т.к. учитывают:
- силы трения и сопротивления колебательному процессу, приводящие к прекращению
колебаний,
- воздействия внешней силы с целью поддержать, продлить колебания.
В лекции определяются основные параметры затухающих и вынужденных колебаний,
вводится понятие механического резонанса.
3

4.

Раздел 1. Затухающие колебания
4

5.

1. Затухающие колебания
1.1. Определение, основные характеристики
Затухающие колебания – это такие колебания, в которых полная энергия колебательного
движения уменьшается с течением времени. Уменьшение именно полной энергии является главным признаком
затухающих колебаний, а не уменьшение их амплитуды. Уменьшение амплитуды колебаний – это следствие уменьшения полной
энергии.
Важная причина уменьшения энергии колебаний – это наличие силы
трения. Сила трения всегда направлена против направления движения
тела и связана со скоростью движения тела v так:
Fтр = - r∙v, r – коэффициент пропорциональности.
Другая форма записи этого уравнения: Fтр = - r∙ẋ = - r∙(dx/dt).
В других колебательных системах могут возникать другие силы,
препятствующие колебательному движению (напр., сопротивление
воздуха для математического маятника и др.). Но при этом важно, что
почти всегда силы сопротивления, как и силы трения, пропорциональны скорости движения тела и
направлены в противоположную сторону.
Поэтому в общем виде можно записать, что сила сопротивления колебательному процессу:
Fсопр = - r∙v.
Численное значение коэффициента пропорциональности r определяется (или задаётся) для
каждого конкретного вида колебательного движения.
5

6.

1. Затухающие колебания
1.2. Дифференциальное уравнение затухающих колебаний
Напомню, строго гармонические колебания происходят под действием так называемой
«возвращающей силы» Fвозвр, которая пропорциональна отклонению х от положения равновесия х = 0 и
всегда направлена против смещения,
Fвозвр = - k∙х,
k – коэффициент пропорциональности, вид его зависит от конкретной задачи.
Знак «минус» означает, что возвращающая сила в любой момент колебаний
направлена к положению равновесия.
Затухающие колебания происходят под действием двух сил: «возвращающей силы» Fвозвр = - k∙х и
силы сопротивления (трения) Fсопр = - r∙v (см. предыдущий слайд).
Уравнение затухающих колебаний в этом случае таково: m∙a = Fвозвр + Fсопр = - k∙х - r∙v.
Или – в дифференциальной форме:
m∙ẍ + r∙ẋ + k∙х = 0.
Обратите внимание: в уравнение затухающих колебаний входят:
- вторая производная ẍ, определяющая результирующую силу;
- первая производная ẋ, определяющая силу сопротивления, которая пропорциональна скорости со
знаком «минус»;
- само смещение от положения равновесия х, которое определяет возвращающую силу,
пропорциональную смещению со знаком «минус».
6

7.

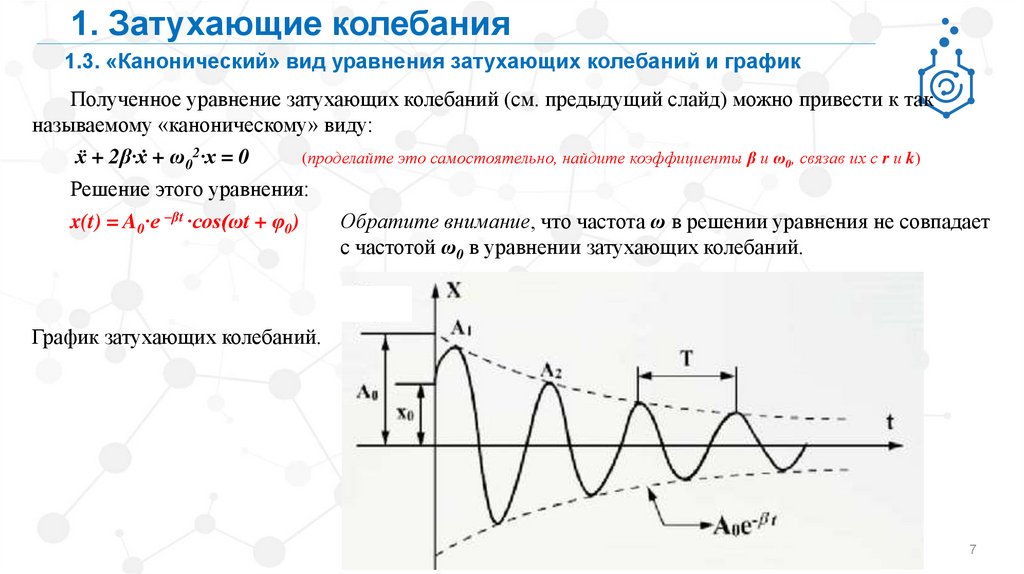
1. Затухающие колебания
1.3. «Канонический» вид уравнения затухающих колебаний и график
Полученное уравнение затухающих колебаний (см. предыдущий слайд) можно привести к так
называемому «каноническому» виду:
ẍ + 2β∙ẋ + ω02∙х = 0
(проделайте это самостоятельно, найдите коэффициенты β и ω0, связав их с r и k)
Решение этого уравнения:
x(t) = A0∙e –βt ∙cos(ωt + φ0)
Обратите внимание, что частота ω в решении уравнения не совпадает
с частотой ω0 в уравнении затухающих колебаний.
График затухающих колебаний.
7

8.

1. Затухающие колебания
1.4. Параметры затухающих колебаний
1). Затухающие колебания остаются гармоническими, т.к. описываются косинусом. Более того,
хотя колебания затухают со временем, их частота и период остаются постоянными!
Но значения ω и Т для затухающих колебаний отличаются от значений ω0 и Т для гармонических
незатухающих колебаний. Связь между этими параметрами такова:
Частота затухающих колебаний меньше собственной частоты
незатухающих гармонических колебаний. Периоды – наоборот, больше.
2). Амплитуда затухающих колебаний, т.е. множитель перед косинусом, экспоненциально снижается со
временем – А(t) = A0∙e-βt. Замечание: затухающие колебания являются не строго гармоническими, т.к. амплитуда их не постоянна
во времени.
Используя график и формулу для затухающих колебаний (см. предыдущий слайд), можно получить
полезное соотношение амплитуд, определяющее скорость их уменьшения за один период колебаний:
Получите эту формулу самостоятельно.
Значение λ = βТ – логарифмический декремент затухания.
Нетрудно получить полезную формулу:
Получите эту формулу также самостоятельно.
8

9.

Раздел 2. Вынужденные колебания
9

10.

2. Вынужденные колебания
2.1. Определение. Дифференциальное уравнение вынужденных колебаний
Определение: Вынужденные колебания – это колебания, происходящие под воздействием
внешней периодической силы.
Внешняя сила есть: Fвнешн = F0∙cos(ωt), где F0 и ω – амплитуда и частота вынуждающей силы.
Внешняя периодическая сила действует на тело, совершающее колебания, одновременно с
«возвращающей» силой и силой сопротивления. Закон Ньютона:
m∙a = Fвозвр + Fсопр + Fвнешн .
Зная выражения для Fвозвр и Fсопр (см. предыдущий раздел 1), нетрудно получить
дифференциальное уравнение вынужденных колебаний:
Коэффициенты β и ω0 определены в разделе 1;
коэффициент f0 = F0 / m.
Обратите внимание: ω0 - собственная частота колебаний,
ω – частота действия вынуждающей силы.
Значения этих частот могут различаться.
В отсутствии силы сопротивления колебательному движения (β=0), уравнение вынужденных
колебаний упрощается:
10

11.

2. Вынужденные колебания
2.2. Решение уравнения вынужденных колебаний. График.
Вновь приведём полное уравнение вынужденных колебаний:
Несмотря на сложный вид уравнения, его установившееся решение (при t→∞) выглядит просто:
x(t) = A∙cos(ωt + φ)
(очень похоже на гармонические колебания!)
Сложности появляются в выражениях для амплитуды А и фазы φ:
Здесь:
ω – частота вынуждающей силы
ω0 – собственная частота колебаний
Вывод: установившиеся вынужденные колебания
происходят с частотой вынуждающей силы ω! а не
с частотой собственных колебаний ω0.
11

12.

2. Вынужденные колебания
2.3. Резонанс
Определение. Резонанс – это резкое увеличение амплитуды вынужденных колебаний.
Резонанс возникает, когда частота вынуждающей силы ω становится
близкой к собственной частоте колебаний ω0, т.е. ω ≈ ω0.
Резонансная частота определяется так:
Напомню, β – коэффициент, характеризующий сопротивление.
В отсутствии сопротивления (β = 0) резонансная частота будет
точно совпадать с собственной: ωРЕЗ = ω0.
Получите формулу для ωрез, используя зависимость амплитуды от частоты:
Это не будет просто!
Типичный график резонанса (справа):
- По мере приближения вынуждающей частоты ω к собственной частоте ω0, амплитуда колебаний А
возрастает.
- Чем меньше сопротивление колебаниям (β→0), тем выше амплитуда А. В отсутствии сопротивления
(β=0) амплитуда колебаний равна бесконечности (А→∞).
- Общая формула для амплитуды колебаний в резонансе:
Получите эту формулу.
12

13.

Спасибо за внимание