Тригонометрические уравнения

1.

Тема.
Тригонометрические
уравнения.
Швецов В.В.

2.

Цели урока:
•Систематизировать, обобщить знания
учащихся по теме «Тригонометрические
уравнения», проверить уровень усвоения
темы.
•Развивать навык решения
тригонометрических уравнений, умение
анализировать, применять полученные
знания к решению заданий по теме урока,
навык самостоятельной работы.
•Воспитывать мотивацию к учению,
развивать познавательный интерес к
предмету.
Швецов В.В.

3.

Уравнение представляет
собой наиболее серьезную и
важную вещь в математике.
Оливер Лодж
Английский физик и
изобретатель.

4.

Повторим решение простейших
тригонометрических уравнений
( с места по цепочке).
Sin x=a, IaI≤1
Sin x=0
Sin x=-1
Sin x=1
x ( 1) arcsin a n, n z
n
x n, n z
x
x
2
2
2 n, n z
2 n, n z

5.

Повторим решение простейших
тригонометрических уравнений
( с места по цепочке).
cos x=a, IaI≤1
x arccos a 2 n, n z
n, n z
cos x=0
x
cos x=-1
x 2 n, n z
cos x=1
x 2 n, n z
2

6.

Повторим решение простейших
тригонометрических уравнений
arcsin( a )
arccos( a )
arcsin a
arccos a
tg x=0
x arctga n, n z
ctg x=0
x arcctga n, n z

7.

а). Выбери правильный ответ
x ( 1) n arcsin 3 n, x n, n z
sin x 3 sin x 0
2
x n, n z
x ( 1) n arcsin 3 n, n z
x arcsin 3 2 n, n z

8.

а). Найди ошибки в решении
3 sin 2 x 5 sin x 2 0
sin х a; a 1
5a 2 5a 2 0
a1 2, a2
sin х 2
1
3
x ( 1) n arcsin 2 n, n z
1
sin х
3
x ( 1)
Ответ:
x ( 1)
n 1
n 1
1
arcsin 2 n, n z
3
1
arcsin n, n z
3

9.

Способы решения тригонометрических уравнений
1. Разложение на множители
2. Метод замены переменной:
сведение к квадратному уравнению;
введение вспомогательного аргумента;
универсальная тригонометрическая подстановка
3. Сведение к однородному уравнению (первой или второй
степени)
4 Путем преобразования тригонометрическими формулами
5. Использование свойств функций, входящих в уравнение:
обращение к условию равенства одноименных
тригонометрических функций;
использование свойства ограниченности функции.
6. Графический

10.

АЛГОРИТМ
решения тригонометрических уравнений
методом введения новой переменной
Шаг 1. Привести уравнение к алгебраическо
му виду относительно одной из тригономе
трических функций
Шаг 2. Обозначить полученную функцию
переменной t (если необходимо, ввести ограни
чения на t)
Шаг 3. Записать и решить полученное алгебра
ическое уравнение.
Шаг 4. Сделать обратную замену
Шаг 5. Решить простейшее тригонометрическое
уравнение

11.

АЛГОРИТМ
решения однородных уравнений
(первой и второй степеней)
Шаг 1. Привести данное уравнение к виду
a) a sin x + b cos x = 0 (однородное уравнение первой степени)
или к виду
б) a sin2 x + b sin x · cos x + c cos2 x = 0 (однородное уравнение второй
степени).
Шаг 2. Разделить обе части уравнения на
а) cos x ≠ 0;
б) cos2 x ≠ 0;
и получить уравнение относительно tg x:
а) a tg x + b = 0;
б) a tg2 x + b tg x + c = 0. Обозначить полученную функцию переменной t
(если необходимо, ввести ограничения на t).
Шаг 4. Сделать обратную замену
Шаг 5. Решить простейшее тригонометрическое уравнение

12.

АЛГОРИТМ решения тригонометрических уравнений
методом
использования различных тригонометрических формул
Шаг 1. Используя всевозможные
тригонометрические формулы, привести данное
уравнение к уравнению, решаемому методами I, II,
III.
Шаг 2. Решить полученное уравнение известными
методами.
1 способ: с помощью формул приведения
2 способ: с помощью вспомогательного аргумента
3 способ: приведение уравнения к однородному
4 cпособ: возведение обеих частей уравнения в
квадрат
5 способ: универсальная подстановка

13.

а). Составить алгоритм решения уравнения
1). 2 cos2 x + sin x+1=0
2). 3 sin2 x - 4sin x cosx + cos2 x=0
3). 2 sin2 x= 3 sin 2x
4). sin x+
3
cos x=2
5). cos2 x -2 cos x=0
6). sin2 x-16=0
7). cos 3x +sin 3x=0
8). 6sin2 x- sin x cos x-cos2 x=3

14.

Самостоятельная работа с взаимопроверкой.
Вариант 1.
Вариант 2.
1). 2 sin x sin x 1 0
1). 6 cos x cos x 1 0
2). sin x sin 2 x 0
2). 4 sin x sin 2 x 0
2
2
2
2

15.

Ответы:(взаимопроверка).
Вариант1
2
( 1)
Ответы:(взаимопроверка).
Вариант2
2
2 n; n
3
1
arccos
2 ;
3
2 n; n Z
6
; Z
n; n
arctg 2 n; n Z
;
arctg
1
2
;

16.

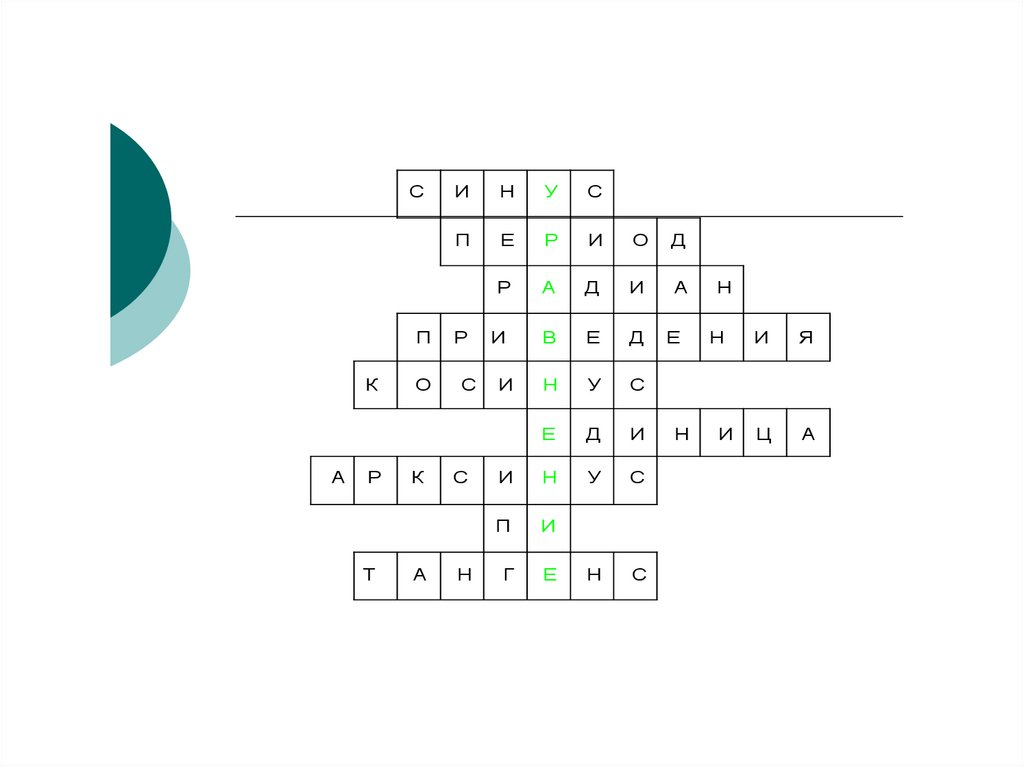
Решение кроссворда.
По горизонтали.
1.Ордината точки на единичной окружности?
2. 2 n для функций у = sinx; y =cosx?
3. Угловая величина дуги, длина которой равна её радиусу.
4.Формулы вида sin (х+2 n )=sin x называются?
5.Абсцисса точки на единичной окружности?.
6.Сумма квадратов синуса и косинуса одного аргумента равна…?.
7. Число из отрезка [-1;1],синус которого равен а?.
8.Математическая постоянная = 3,14? .
9. Отношение синуса числа к косинусу того же числа.

17.

18.

С
П
К
А
Р
Т
О
К
А
И
Н
У
С
П
Е
Р
И
О
Д
Р
А
Д
И
А
В
Е
Д
Н
У
С
Е
Д
И
И
Н
У
С
П
И
Г
Е
Н
С
Р
С
С
Н
И
И
Е
Н
Н
Н
И
И
Я
Ц
А

19.

Рефлексия деятельности на уроке
Какие умения вы сегодня тренировали?
Какую цель вы ставили перед собой?
Вы достигли поставленной цели?
Какие знания вы использовали при
выполнении заданий?
• Какие затруднения возникали в процессе
работы над заданиями?

20.

Станислав Коваль :
“Уравнение - это золотой ключ,
открывающий все математические
сезамы”

21.

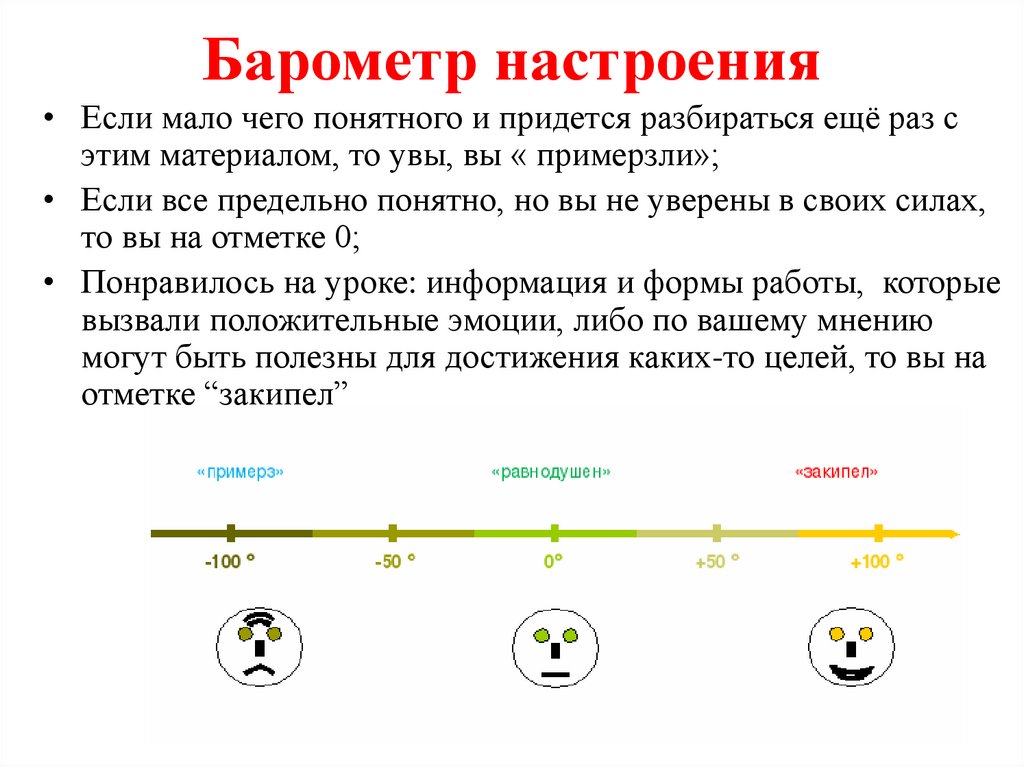
Барометр настроения
• Если мало чего понятного и придется разбираться ещё раз с
этим материалом, то увы, вы « примерзли»;
• Если все предельно понятно, но вы не уверены в своих силах,
то вы на отметке 0;
• Понравилось на уроке: информация и формы работы, которые
вызвали положительные эмоции, либо по вашему мнению
могут быть полезны для достижения каких-то целей, то вы на
отметке “закипел”

22.

Домашнее задание:
Решить различными способами
уравнения:
• sin4x - sin2x = 0,
• cos2x - cos4x = 0.
22

23.

Спасибо
за урок!