Similar presentations:
Методы решения тригонометрических уравнений
1.
Методы решениятригонометрических
уравнений
2.
Методы решения тригонометрическихуравнений
1.Приведение уравнения к однородному.
2.Разложение левой части уравнения на множители.
3.Приведение к квадратному уравнению.
4.Возведение обеих частей уравнения в квадрат.
2
3.
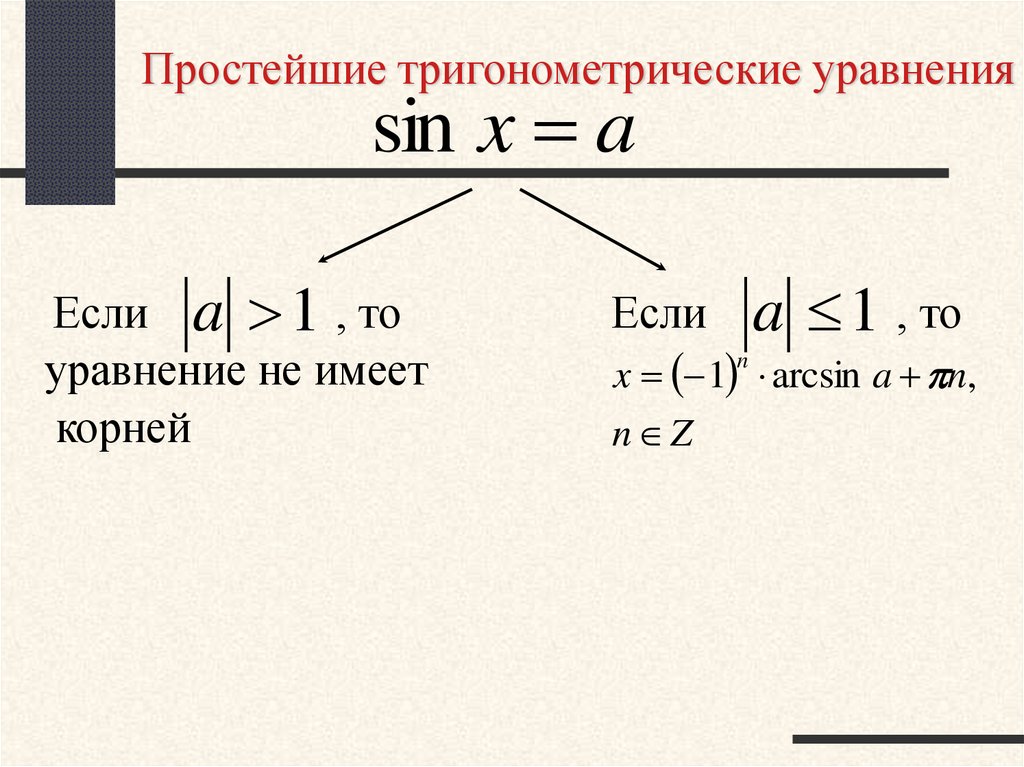
Простейшие тригонометрические уравненияsin x a
Если a 1 , то
уравнение не имеет
корней
a 1 , то
Если
x 1 arcsin a n,
n Z
n
4.
Простейшие тригонометрические уравненияЧастные случаи
sin x 1
x
2
2 k , k Z
sin x 0
sin x 1
x k , k Z
x
2
2 k , k Z
5.
Простейшие тригонометрические уравненияcos x a
Если a 1 , то
уравнение не имеет
корней
Если
a 1 , то
x arccos a 2 n,
n Z
6.
Простейшие тригонометрические уравненияЧастные случаи
cos x 1
cos x 0
x 2 k , k Z
x
2
k , k Z
cos x 1
x 2 k , k Z
7.
Простейшие тригонометрические уравненияtgx a
ctgx a
x arctga n, n Z
x arcctga n, n Z
8.
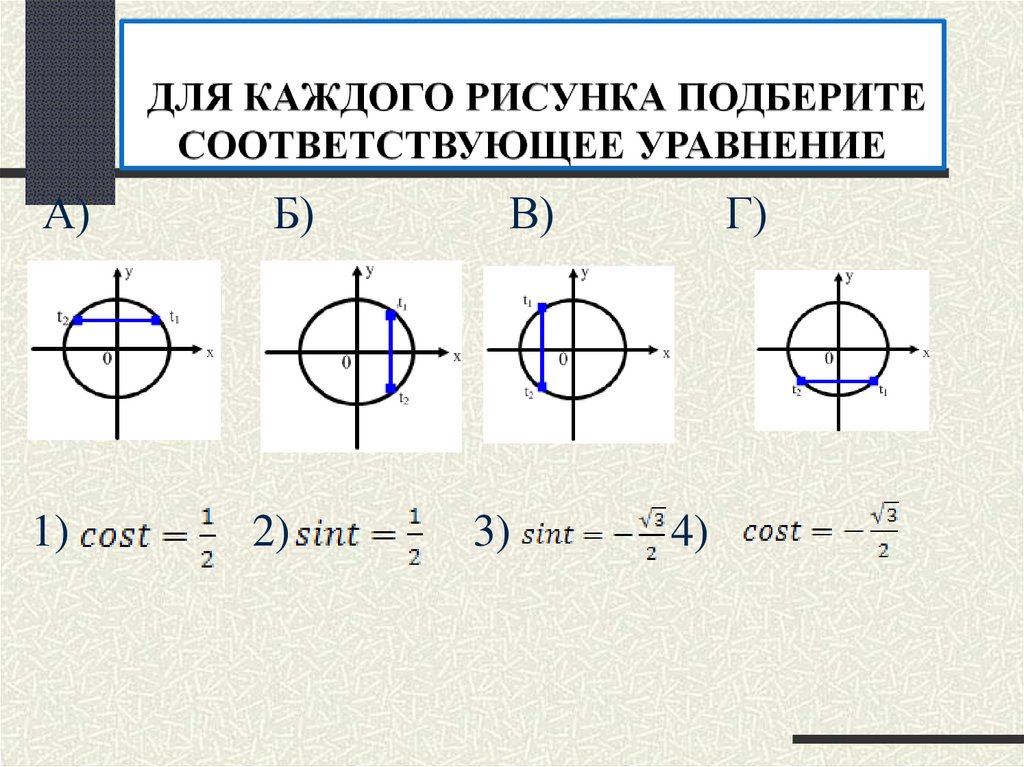
А)Б)
1)
2)
В)
3)
Г)
4)
9.
А)2)
Б)
1)
В)
4)
Г)
3)
10.
π+2πk, k ∈ Z
2
1) sin x = 0
а)
2) cos x = -1
б)
3) sin x = 1
в)
π
+πk, k ∈ Z
2
4) tg x = 1
г)
π+ 2πk, k∈ Z
д)
π
+πk, k ∈ Z
4
5) ctgx = 0
πk, k∈ Z
11.
12.
Методы решения тригонометрическихуравнений
Некоторые типы тригонометрических уравнений.
1. Уравнения, сводящиеся к квадратным,
относительно cos х = t, sin х = t.
A sin2 x + B cosx + C = 0
A cos2 x + В sinx + C = 0
Решаются методом введения новой переменной.
2.Однородные уравнения первой и второй степени.
I степени.
II степени.
A sinx + B cosx = 0 : cosx
A tg x + B = 0
A sin2 x + B sinx cosx + A cos2 x = 0 : cos2x
A tg2 x + B tgx + C = 0
Решаются методом разложения на множители и методом
введения новой переменной.
12
13.
Методы решения тригонометрическихуравнений
3. Уравнение вида:
А, В, С 0
А sinx + B cosx = C.
Применимы все методы.
4. Понижение степени.
А cos2x + Вcos2 x = C.
A cos2x + B sin 2 x = C.
Решаются методом разложения на множители.
2
A sin2x + B sin x = C.
A sin2x + Bcos2 x = C.
Сводятся к однородным уравнениям С = С(sin 2 x+ cos2 x )
13
14.
Методы решения тригонометрическихуравнений
Формулы.
Универсальная подстановка.
x
2
cosx
=
;
sinx=
;
x
2
x
1+ tg
1+ tg2
2
2
1-tg2
x
2tg
2
2tg
tgx=
x
2
1− tg 2
x
2
;
х + 2 n;
Проверка обязательна!
Понижение степени.
cos x = (1 + cos2x ) : 2
sin 2 x
= (1 – cos 2x) : 2
2
Метод вспомогательного аргумента.
√2
С= a +b ;
a cosx +b sinx заменим на C sin(x+ ), где
b
а
;
- вспомогательный аргумент.
cos
=
sin = ;
С
2
С
14
15.
Проблемы ,возникающие при решениитригонометрических уравнений
1.Потеря корней:
делим на g(х).
опасные формулы (универсальная подстановка).
Этими операциями мы сужаем область определения.
2. Лишние корни:
возводим в четную степень.
умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.
15
16.
Задача. Решите уравнениеразличными способами: sin x – cos x = 1.
16
17.
Способ первый. Приведение уравнения коднородному.
sin x – cos x = 1
sin x = 2 sin x/2 cos x/2,
cos x = cos 2 x/2 - sin 2 x/2,
1 = sin 2 x/2 + cos2 x/2.
Это однородное уравнение первой степени. Делим обе части этого
уравнения на
,
т.к., если
что противоречит тождеству
.
Получим:
17
18.
Способ второй. Разложение левой частиуравнения на множители: sin x – cos x = 1
sin x = 2 sin x/2 cos x/2
cos x = 2cos 2 x/2 - 1
Далее так, как в первом способе.
18
19.
Способ третий. Приведение к квадратномууравнению относительно одной функции.
sin x - cos x = 1
Возведем в квадрат:
или
19
20.
Внимание! При решении уравнения обе части уравнениявозводились в квадрат, что могло привести к появлению
посторонних решений, поэтому необходима проверка.
.
Сделаем проверку
Полученные решения эквивалентны объединению трёх решений
Первое и второе решение совпадают с ранее полученными, поэтому не
являются посторонними. Проверять не будем.
Проверим:
Левая часть:
а правая часть уравнения равна 1, следовательно это решение является посторонним.
20
21.
Способ четвертый.Возведение обеих частейуравнения в квадрат.
sin x – cos x = 1
sin2x - 2sin x cos x + cos2 x = 1, sin2 x + cos2x = 1
1 – 2sin x cos x = 1,
2sin x cos x = 0,
sin x = 0
или cos x =0
x = n, n Z
x= /2 + n, n Z
Ответ: x = n, n Z, x= /2 + n, n Z.
21
22.
Проверь себя !Решите самостоятельно, применяя разные
способы решения одного и того же
тригонометрического уравнения:
1. sin2x + cosx = 0 ;
2. 3 sin x – cos x = 0
3. sin6x + sin3x = 0;
4. sin2x +cos2x = 1;
5. 3sin x + cos x = 1.
22
23.
Человеку, изучающему алгебручасто
полезнее решить одну и ту же задачу тремя
различными способами, чем решать три –
четыре различные задачи. Решая одну задачу
различными способами, можно путем
сравнивания выяснить, какой из них короче
и эффективнее. Так вырабатывается опыт.
У. У. Сойер
/английский математик и педагог XX века/
23
24.
Желаю успеха!24






















 mathematics
mathematics








