Площадь трапеции

1.

2.

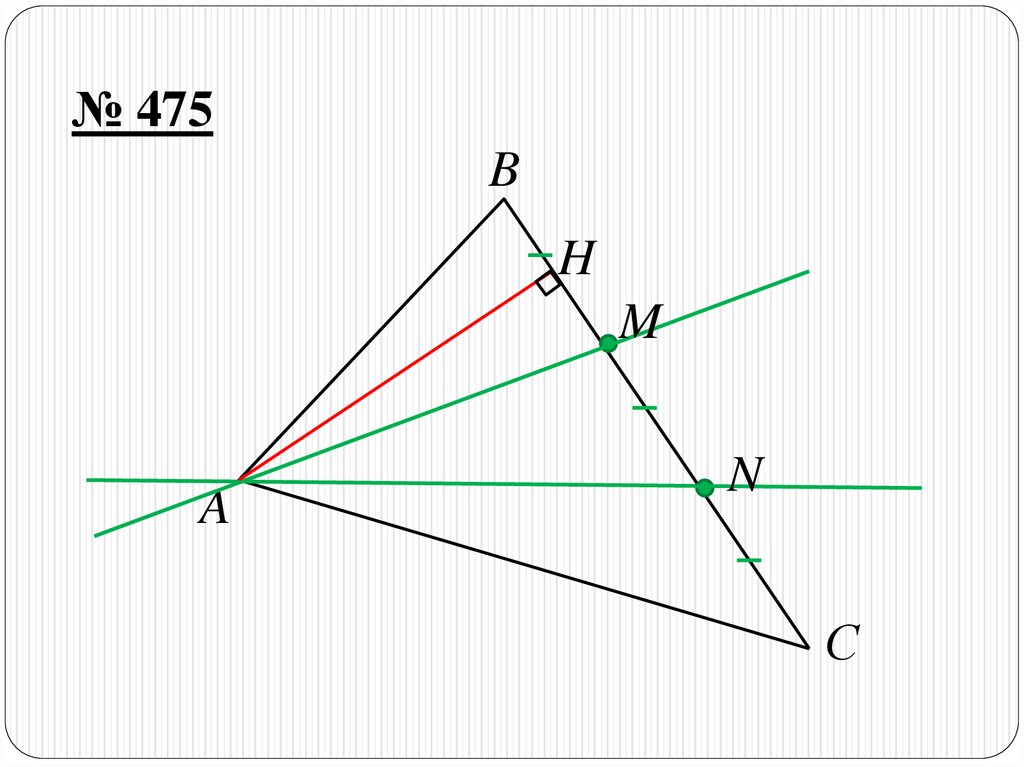
№ 475
B
H
M
A
N
С

3.

Как найти площадь произвольного
многоугольника, составленного из нескольких
треугольников?
S₁
S₂
S₃
S4
S5
S S1 S2 S3 S4 S5

4.

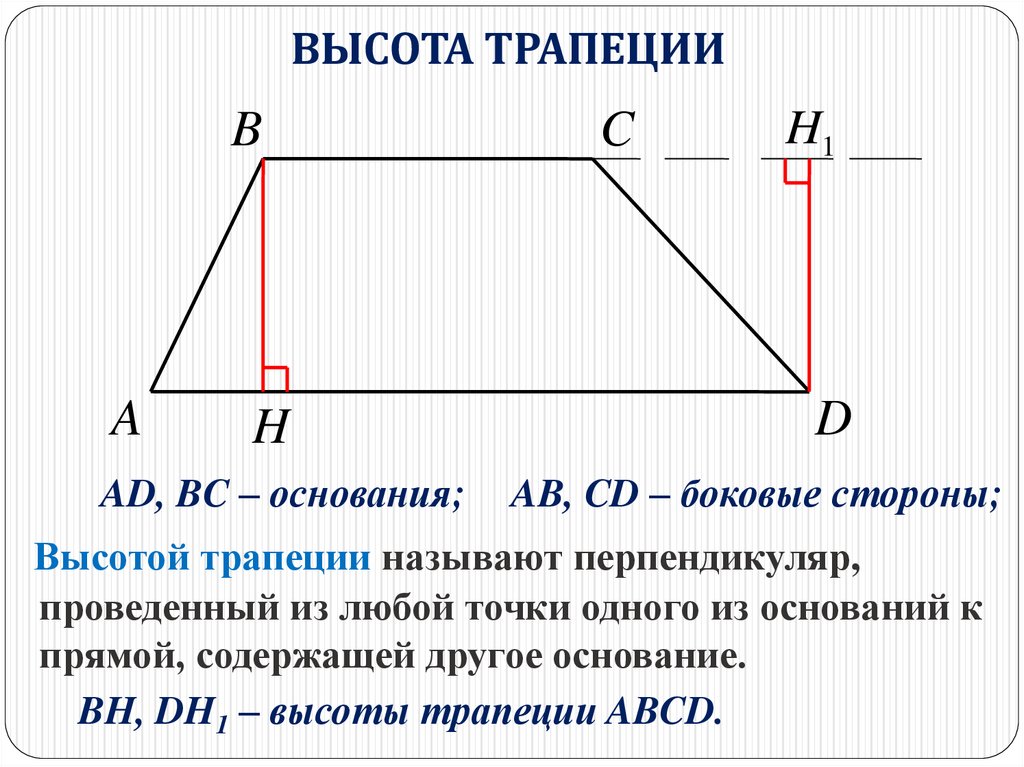
ВЫСОТА ТРАПЕЦИИ
B
A
H
AD, BC – основания;
C
H1
D
AB, CD – боковые стороны;
Высотой трапеции называют перпендикуляр,
проведенный из любой точки одного из оснований к
прямой, содержащей другое основание.
BH, DH1 – высоты трапеции ABCD.

5.

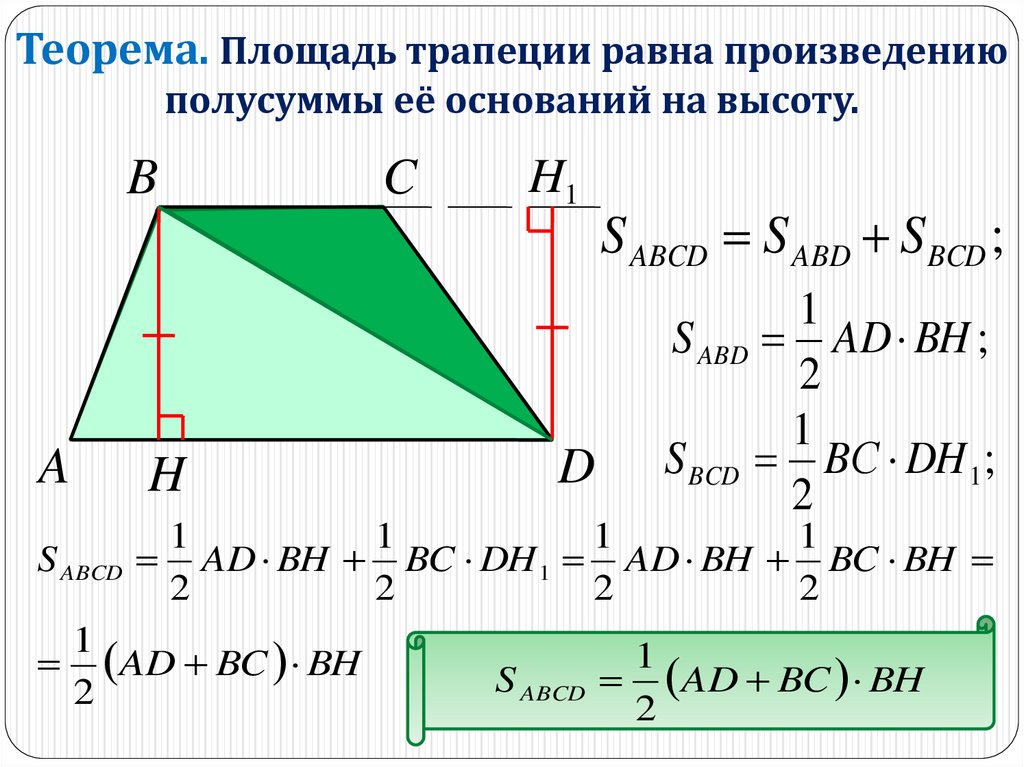
Теорема. Площадь трапеции равна произведению
полусуммы её оснований на высоту.
B
A
S ABCD
H
C
H1
D
S ABCD S ABD S BCD ;
1
S ABD AD BH ;
2
1
S BCD BС DH 1 ;
2
1
1
1
1
AD BH BC DH 1 AD BH BC BH
2
2
2
2
1
AD BC BH
2
S ABCD
1
AD BC BH
2

6.

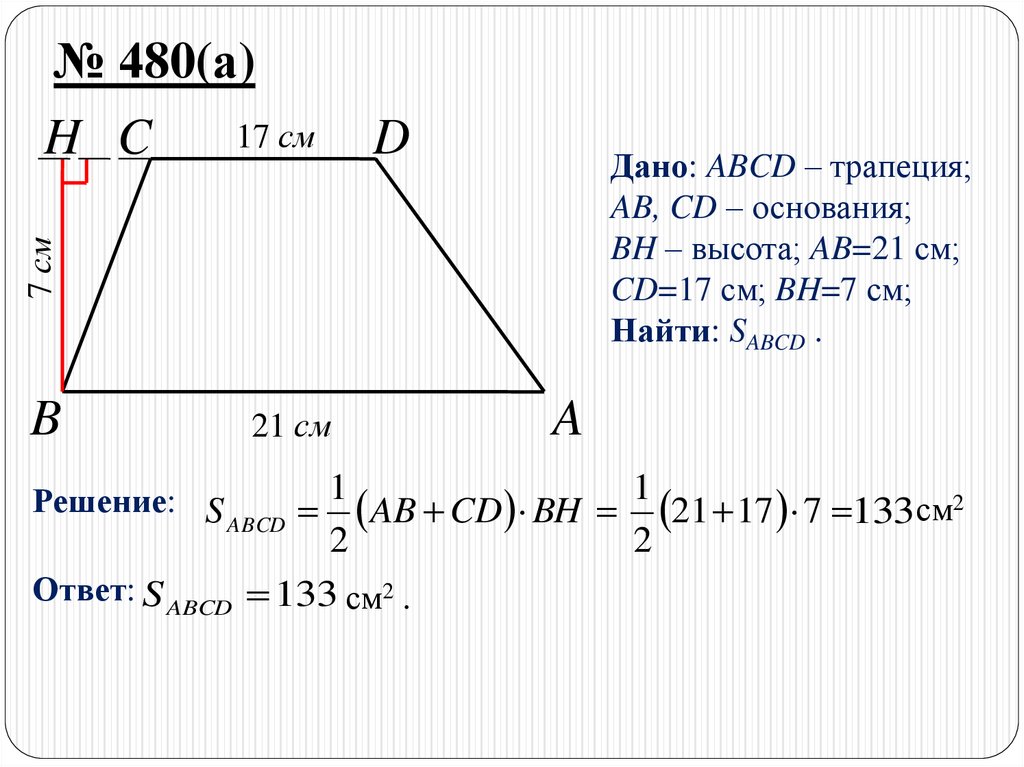
D
Дано: ABCD – трапеция;
AB, CD – основания;
BH – высота; AB=21 см;
CD=17 см; BH=7 см;
Найти: SABCD .
7 см
№ 480(а)
17 см
H C
B
21 см
A
1
1
2
Решение: S
см
AB
CD
BH
21
17
7
133
ABCD
Ответ: S ABCD
2
133 см2 .
2

7.

№ 480(б)
A
2 см
B
Дано: ABCD – трапеция;
AB, CD – основания;
AB=2 см; CD=10 см;
DA=8 см; D 30
Найти: SABCD .
30
D
H
10 см
C
Решение: 1) проведем высоту AH;
2) рассмотрим ADH : D 30 след.
1
AH AD 4 см (свойство прямоуг. треуг.);
2
1
1
S ABCD AB CD AH 2 10 4 24 см2
2
2
Ответ: S
2
ABCD 24 см .

8.

№ 480(в)
A
B
8 см
5 cм
D
Дано: ABCD – трапеция;
AB, CD – основания;
BC AB; AB=5 см;
BC=8 см; CD=13 см;
Найти: SABCD .
C
13 см
1
1
2
Решение: S
см
AB
CD
BС
5
13
8
72
ABCD
2
Ответ: S ABCD 72 см2 .
2