Similar presentations:
Теорема Вариньона
1. Теорема Вариньона
ТЕОРЕМАВАРИНЬОНА
Проект выполнил
ученик 8 класса
ЯСОШ Якушенко
Саша, под
руководством
Якушенко Татьяны
Андреевны
2. Цель
◦Узнать дополнительныйтеоретический материал,
который может упростить
решение задач и расширить мой
кругозор.
3. Задачи
◦1) Найти тему для проекта◦2)Изучить и доказать теорему
Вариньона и некоторые следствия
◦3)Решить задачи и доказать
некотоырые утверждения из
школьной программы с помощью
данной теоремы
◦4)Оформить проект
4. Актуальность
◦ В 8 классе я участвовал во многихолимпиадах по математике, задания в
которых затрагивали много тем из
углубленных программ обучения.
Поэтому я захотел узнать что-то новое,
что позволит решать задачи более
рациональным способом и сократит
время решения задач.
5. Пьер Вариньон
6. Формулировка
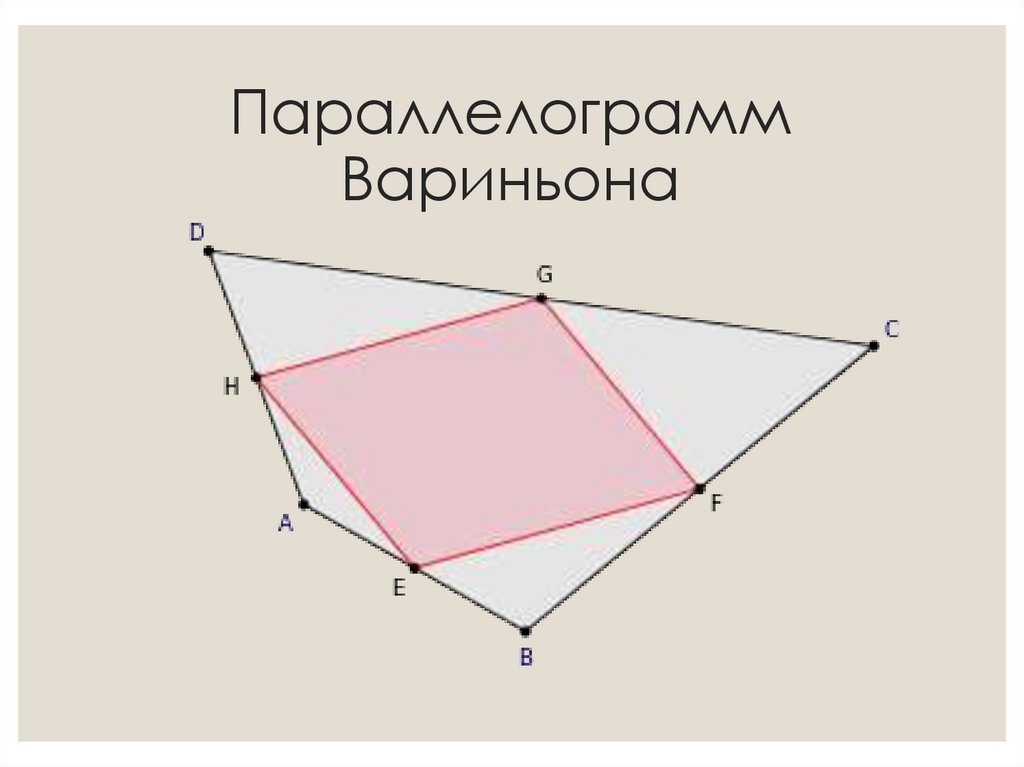
◦ Четырёхугольник, вершины которогосовпадают с серединами сторон
произвольного четырёхугольника,
является параллелограммом, стороны
которого параллельны диагоналям
исходного четырёхугольника.
7. Параллелограмм Вариньона
8.
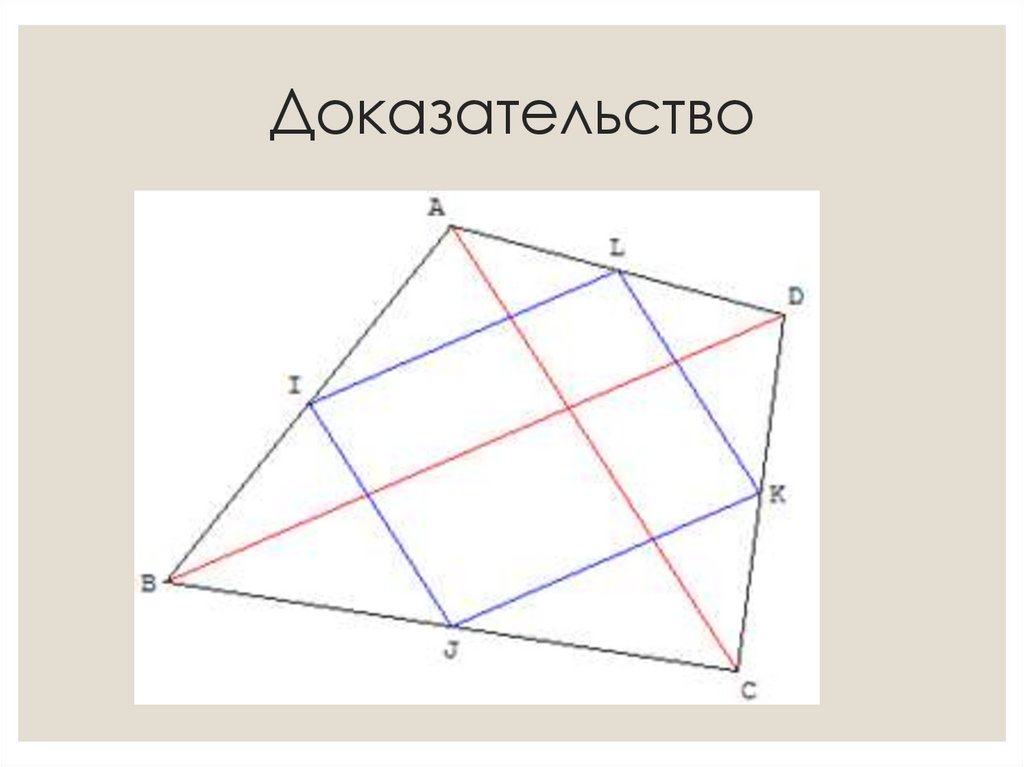
9. Доказательство
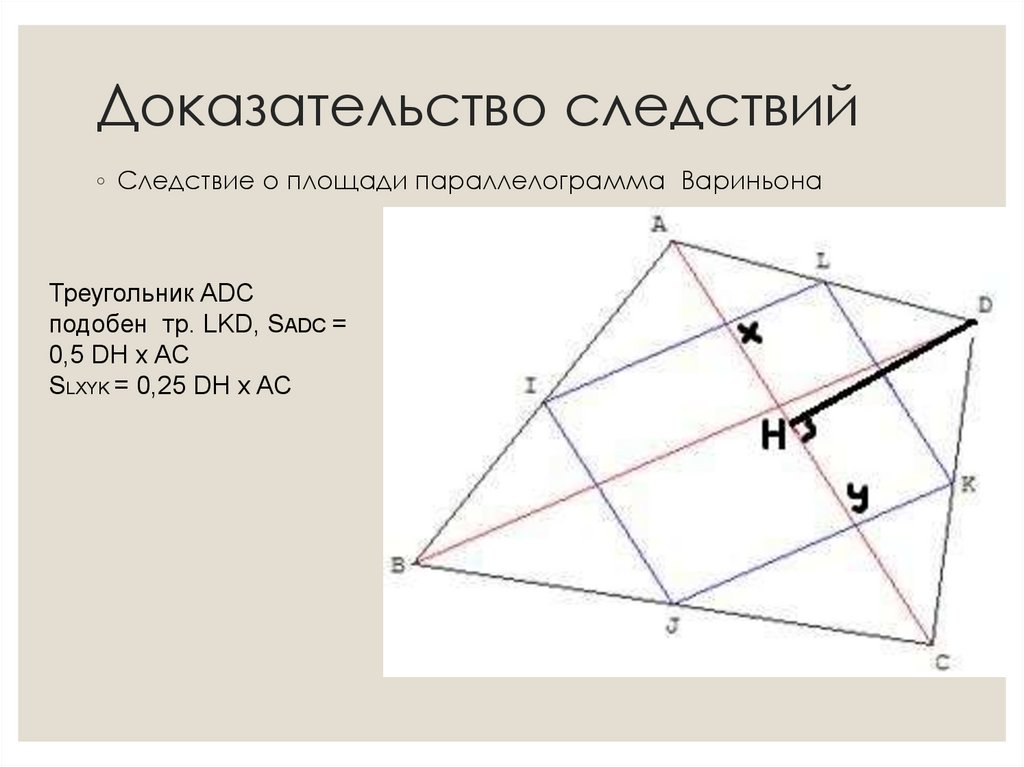
10. Доказательство следствий
◦ Следствие о площади параллелограмма ВариньонаТреугольник ADC
подобен тр. LKD, SADC =
0,5 DH x AC
SLXYK = 0,25 DH x AC
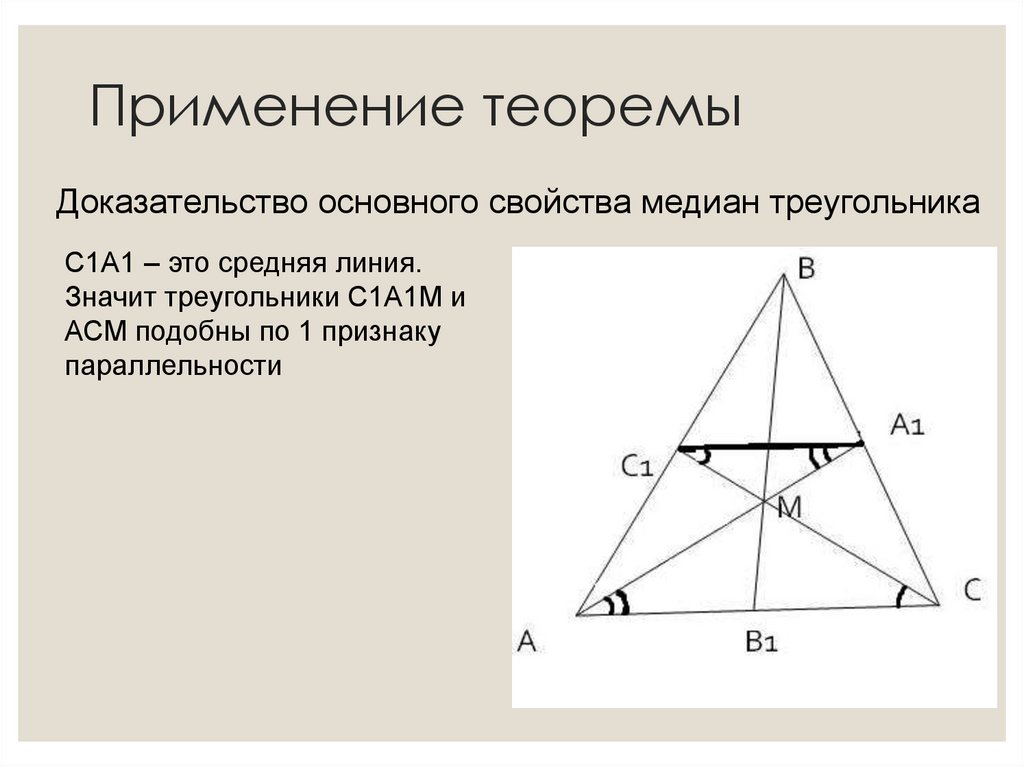
11. Применение теоремы
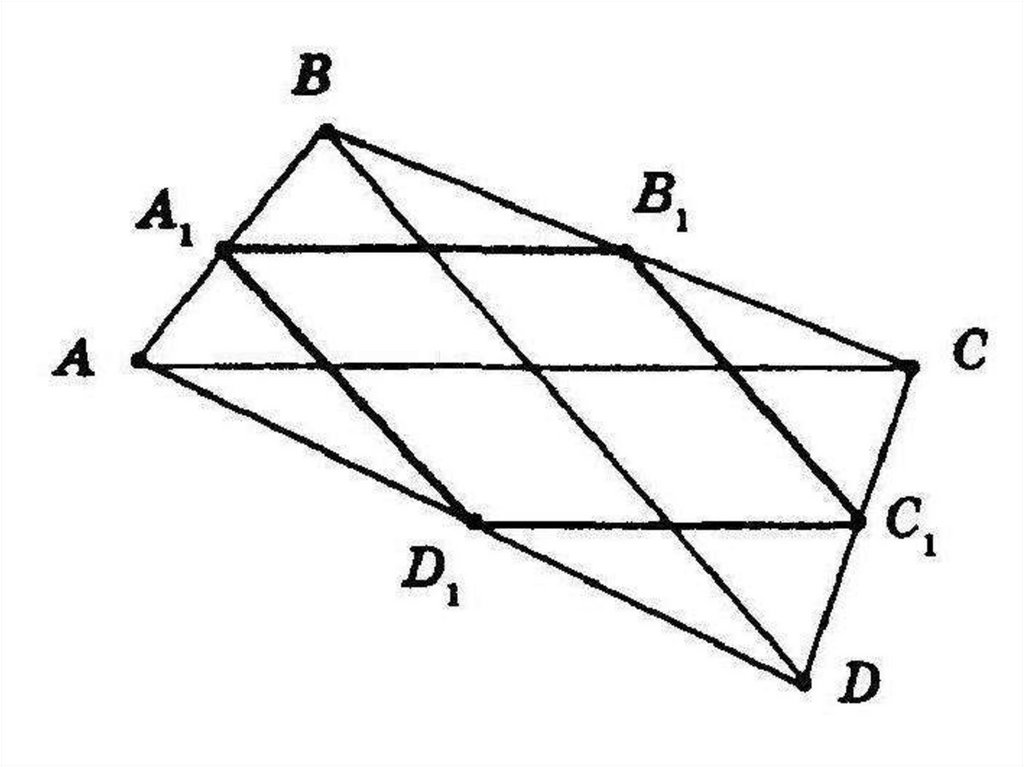
Доказательство основного свойства медиан треугольникаС1А1 – это средняя линия.
Значит треугольники С1А1М и
АСМ подобны по 1 признаку
параллельности
12. Простое доказательство
проведём две медианы AM и CDтреугольника ABC. Пусть О – точка
их пересечения. Середины сторон
невыпуклого четырехугольника
АBCО – точки K, L, M и D –
вершины параллелограмма, причем
точкой пересечения его диагоналей
KM и LD для этой конфигурации
будет точка пересечения медиан О.
Итак, AK = MO = OK и CL = DO = OL,
т.е. точка О делит каждую из медиан
AM и CD в отношении 2:1.
13. Решение задач
1) Докажите, что если диагоналичетырёхугольника равны, то его
площадь равна произведению
средних линий.
14.
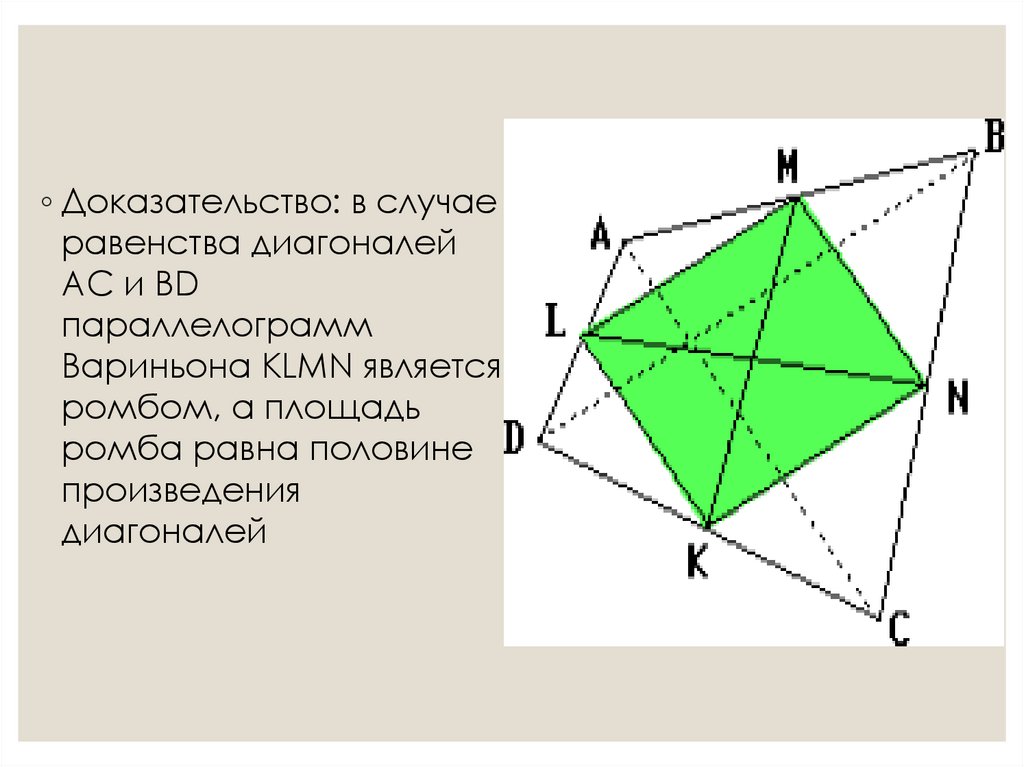
◦ Доказательство: в случаеравенства диагоналей
AC и BD
параллелограмм
Вариньона KLMN является
ромбом, а площадь
ромба равна половине
произведения
диагоналей
15.
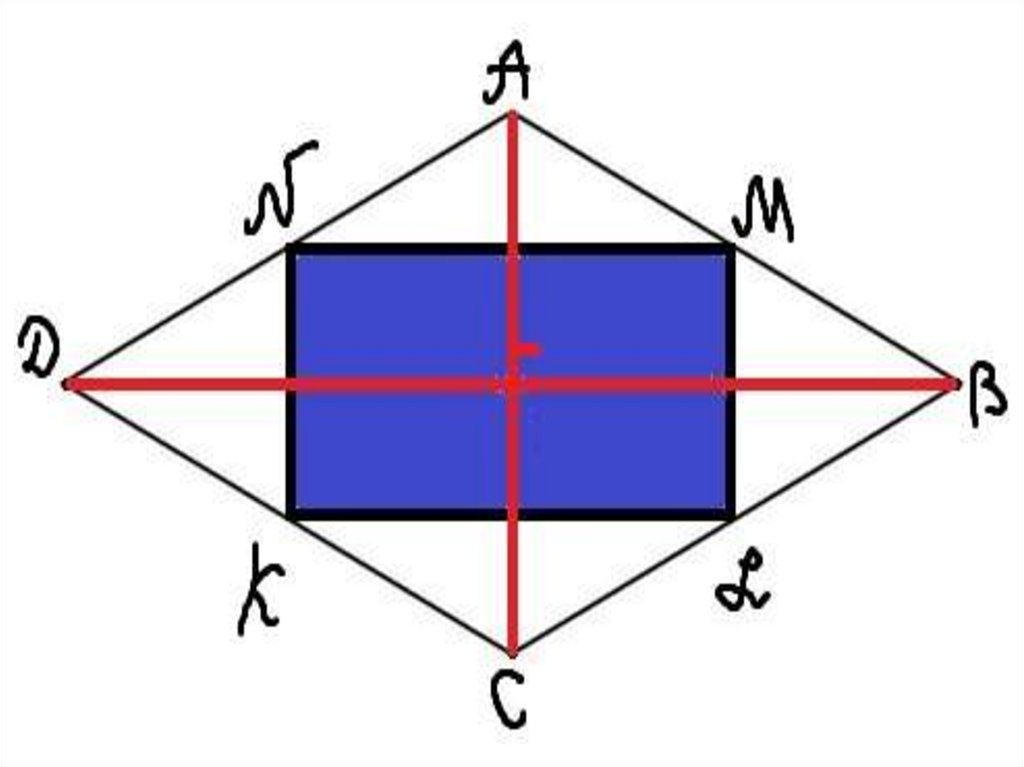
◦2)Докажите, что◦а) середины сторон
прямоугольника являются
вершинами ромба. И
наоборот;
◦ б) середины сторон ромба
являются вершинами
прямоугольника.
16.
17.
18.
◦3) У четырехугольника диагоналиравны a и b. Найдите периметр
четырехугольника, вершинами
которого являются середины сторон
данного четырехугольника.
19.
20. Дальнейшие перспективы развития проекта
Я понял, что геометрия гораздо шире и чтобыучаствовать в олимпиадах ее нужно знать в
большем объеме . В будущем я планирую
дополнить этот проект большим количеством
дополнительного материала (следствия,
задачи)
21. Ожидаемые результаты
Мне будет проще решать задачи и школьные,и олимпиадные. Буду дальше наращивать
объем внешкольных знаний по математике,
другим предметам
22. Вывод
Я узнал новую теорему, научился решатьзадачи с ее помощью, знаю, как доказать
свойство медиан треугольников и некоторые
следствия из теоремы, проделал большую
работу. Теперь я могу решать задачи не
только из школьной программы.
23. Литература
◦ https://ru.wikipedia.org/wiki/Вариньон,_Пьер◦ https://ru.wikipedia.org/wiki/Теорема_Вариньона_(геометрия)
◦ https://lycu1580.mskobr.ru/attach_files/upload_users_files/5e87128274
cce.pdf https://5terka.com/images/geom8/8class-395.jpg
















 mathematics
mathematics








