Similar presentations:
Теорема Вариньона и ее применение
1.
Теорема Вариньона и ееприменение
2.
Пьер Вариньон (1654–1722)Пьер Вариньон родился во Франции в 1654
году. Обучался в иезуитском коллеже и
университете в Кане, где стал магистром в 1682
году.
Вариньон
готовился
к
религиозной
деятельности, но, изучая сочинения Эвклида
и Декарта, увлекся математикой и механикой.
Труды Вариньона посвящены теоретической
механике, анализу бесконечно малых величин,
геометрии, гидромеханике и физике.
В 1687 Вариньон представил в Парижскую
Академию наук сочинение «Проект новой
механики...», в котором сформулировал закон
параллелограмма сил.
В 1725 в Париже был издан трактат Вариньона
«Новая
механика
или
статика»,
представляющий
собой
систематическое
изложение учения о сложении и разложении
сил, о моментах сил и правилах оперирования
ими, почти без изменений сохранившееся в
учебниках статики до нашего времени. Написал
учебник по элементарной геометрии.
3.
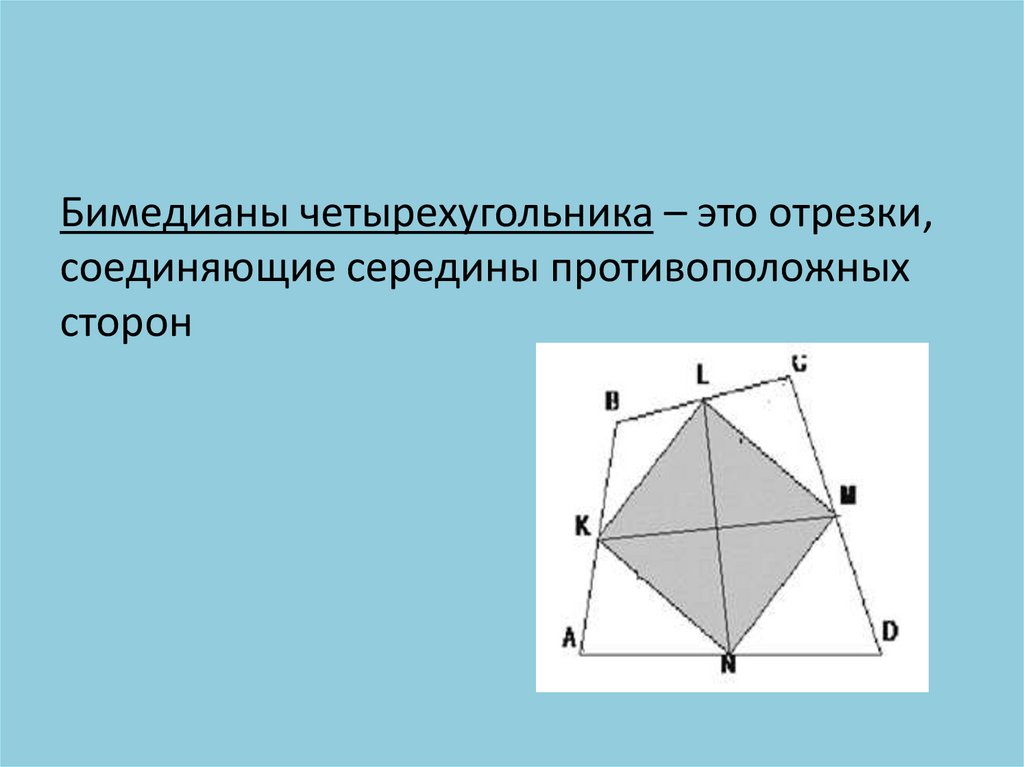
Бимедианы четырехугольника – это отрезки,соединяющие середины противоположных
сторон
4.
Теорема ВариньонаЧетырехугольник, образованный путем
последовательного соединения середин сторон
выпуклого четырехугольника, является
параллелограммом, и его площадь равна
половине площади данного четырехугольника.
Такой параллелограмм называется
параллелограммом Вариньона данного
четырехугольника
5.
Следствие 1Параллелограмм Вариньона является
прямоугольником тогда и только тогда, когда
в исходном четырехугольнике
а) диагонали перпендикулярны;
б) бимедианы равны.
6.
Следствие 2Параллелограмм Вариньона является
ромбом тогда и только тогда, когда в
исходном четырехугольнике
1) диагонали равны;
2) бимедианы перпендикулярны.
7.
Следствие 3Параллелограмм Вариньона является
квадратом тогда и только тогда, когда в
исходном четырехугольнике
а) диагонали равны и перпендикулярны;
б) бимедианы равны и перпендикулярны.
8.
Следствие 4Бимедианы четырехугольника и отрезок,
соединяющий середины диагоналей,
пересекаются в одной точке и делятся этой
точкой пополам.
9.
Теорема ЭйлераДля четырехугольника сумма квадратов всех
сторон равна сумме квадратов диагоналей
плюс учетверённый квадрат отрезка,
соединяющего середины диагоналей, то
есть
10.
Теорема о бабочкахСуммы площадей накрест лежащих
четырехугольников, образованных
пересечением бимедиан LN и KM выпуклого
четырехугольника ABCD равны.
11.
ТеоремаМедианы в треугольнике пересекаются в
одной точке и делятся в ней в отношении 2:1,
считая от вершины.
12.
Задача 1У четырехугольника диагонали
равны a и b. Найдите периметр
четырехугольника, вершинами которого
являются середины сторон данного
четырехугольника.
13.
Задача 2Докажите, что если диагонали
четырехугольника равны, то его площадь
равна произведению бимедиан.
14.
Задача 3В выпуклом пятиугольнике ABCDE середины
сторон AB и CD, BC и DE соединены
отрезками. K, L – середины этих отрезков.
Доказать, что отрезок KL параллелен пятой
стороне AE и составляет ¼ от неё.
15.
Задача 4Докажите, что сумма квадратов диагоналей
четырёхугольника в два раза больше суммы
квадратов его бимедиан
16.
Задача 5Диагонали четырёхугольника ABCD равны
d1 и d2, а бимедианы равны между собой.
Найдите площадь четырёхугольника
17.
Задача 6Докажите, что все четырёхугольники,
имеющие общие середины сторон,
равновелики
















 mathematics
mathematics