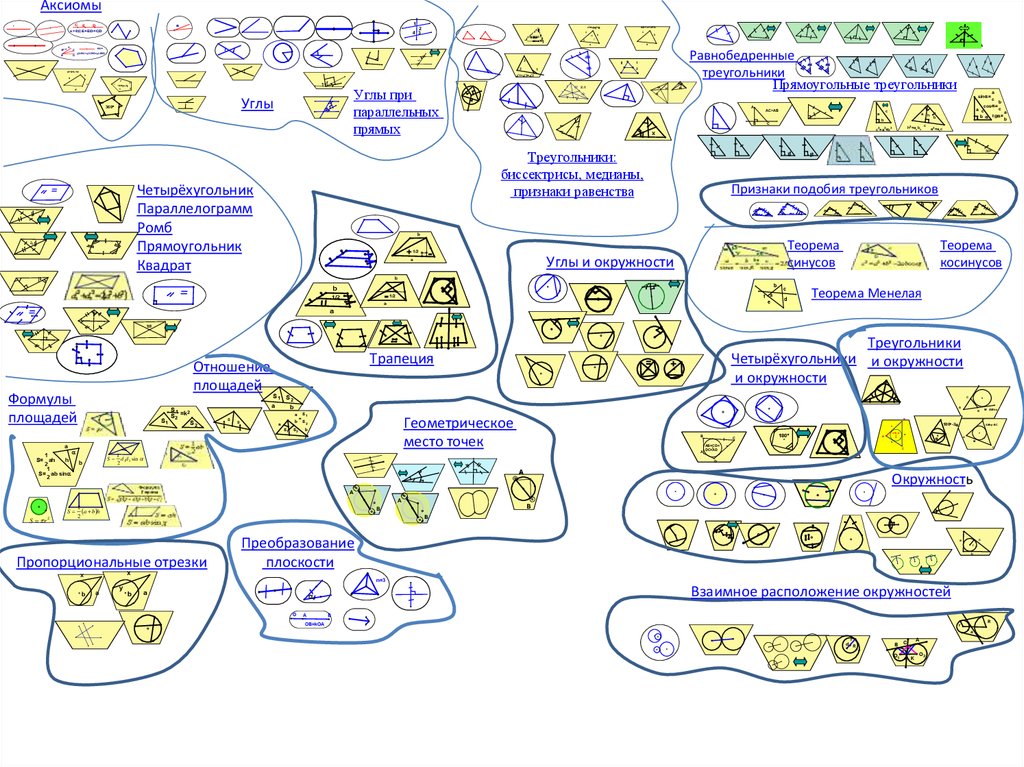
Шпаргалка. Аксиомы

1.

Аксиомы
C
E
1
2
4 3
D
s>0;СE+ED=CD
a-b<c<a+b
c>a >
c
c
b
>0
D
a
180
C
B
b
a
A
Равнобедренные
треугольники
Прямоугольные треугольники
ABC+ CBD= ABD
3
180
1
2
a+b+c>d
2
1
1= 2+ 3
b
a
2
c
1
3
180 n-2
5
d
Углы
360
А
В
АС>АВ
с
а
а
h
b
С
h2=acbc
с2=а2+b2
x
Треугольники:
биссектрисы, медианы,
признаки равенства
Четырёхугольник
Параллелограмм
Ромб
Прямоугольник
Квадрат
ZO
2:1
Углы при
параллельных
прямых
4
с
a
sin =
c
b
cos =
c
а с
a
b tg =
b
b
a2=acc
30
Признаки подобия треугольников
b
+
1/2
a
-
Теорема
синусов
Углы и окружности
Теорема
косинусов
b
b
b
-
1/2
f a
e
1/2
a
c
d
Теорема Менелая
a
Отношение
площадей
Формулы
площадей
S1
Трапеция
S1 S
2
b
C
A
a
S2
S
S
b
a
S2
=
M AM=p
B
S1
Геометрическое
место точек
S2
b
а
S
Треугольники
Четырёхугольники и окружности
и окружности
+
a
S1
2
S 2 =k
S1
1
S= ah
h
b
2
1
S= ab sin
2
=
B
B
180 -2
c
B
C
180
A
c+b-a
2
a
AM=p-BC
A
M
b
AB+CD=
A DC+AD
1
d1d 2 sin
2
C
C
D
A
Окружность
А
А
S
S r 2
1
a b h
2
В
Пропорциональные отрезки
x
x
b
B
В
Преобразование
плоскости
c
a
r
b
n=3
a
y
b
a
Взаимное расположение окружностей
О
А
В
ОВ=kОА
R
r
a
r
d
R
В
О1
А
С
К
О2

2.

Аксиомы
Существует прямая и точка, не принадлежащая прямой.
Через две точки проходит одна и только одна прямая
Через точку, не лежащую на прямой, проходит только одна прямая, параллельная данной.
Две прямые пересекаются не более, чем в одной точке.
C
E
Если точка лежит между двумя другими на прямой, то CE+ED=CD.
D
s>0;СE+ED=CD
>0
A
180
C
D
B
ABC+ CBD= ABD
Величина развёрнутого угла 1800. Луч, выходящий из вершины угла и лежащий внутри угла
делит его на два угла, градусные величины которых в сумме равны градусной величине
исходного угла.
Фигура, образованная конечным набором отрезков, расположенных так, что конец первого
является началом второго , конец второго началом третьего и т.д., называется ломаной.
Многоугольник называется выпуклым, если вместе с любыми двумя его точками он содержит
соединяющий их отрезок.
a+b+c>d
b
a
c
Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом
последнего
d
2
1
3
Сумма внутренних углов выпуклого n-угольника равна 180° • (п - 2).
180 n-2
5
4
Сумма внешних углов п-угольника равна 360°.
360
На главную

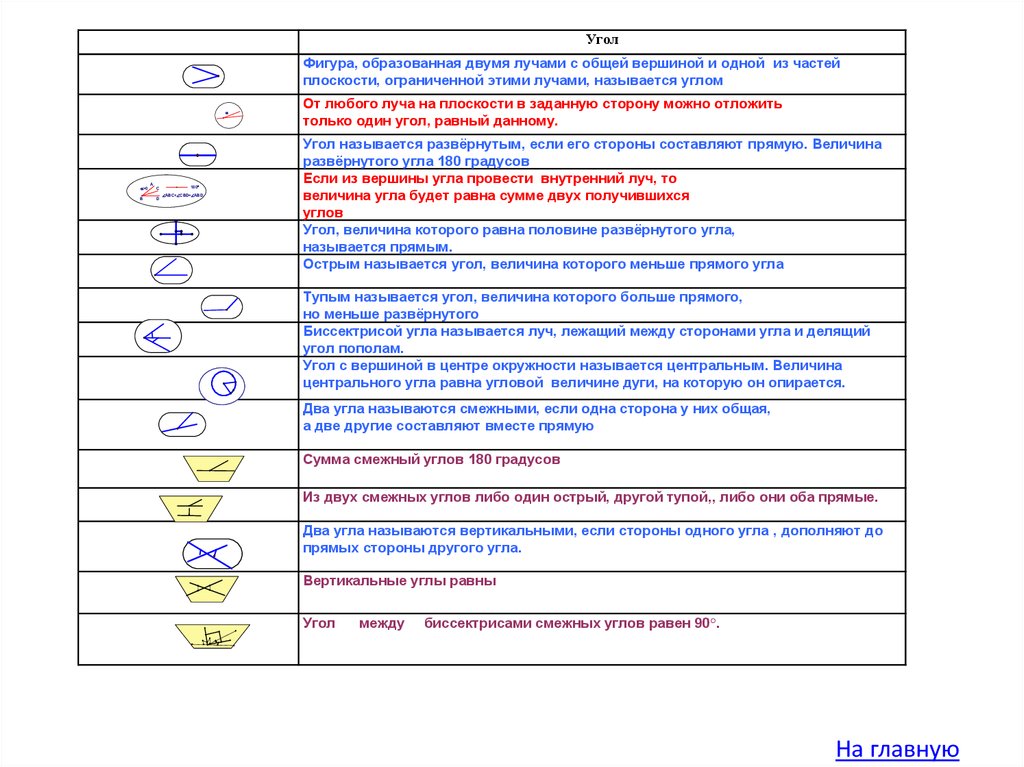
3.

Угол
Фигура, образованная двумя лучами с общей вершиной и одной из частей
плоскости, ограниченной этими лучами, называется углом
>0
B
A
C
D
180
ABC+ CBD= ABD
От любого луча на плоскости в заданную сторону можно отложить
только один угол, равный данному.
Угол называется развёрнутым, если его стороны составляют прямую. Величина
развёрнутого угла 180 градусов
Если из вершины угла провести внутренний луч, то
величина угла будет равна сумме двух получившихся
углов
Угол, величина которого равна половине развёрнутого угла,
называется прямым.
Острым называется угол, величина которого меньше прямого угла
Тупым называется угол, величина которого больше прямого,
но меньше развёрнутого
Биссектрисой угла называется луч, лежащий между сторонами угла и делящий
угол пополам.
Угол с вершиной в центре окружности называется центральным. Величина
центрального угла равна угловой величине дуги, на которую он опирается.
Два угла называются смежными, если одна сторона у них общая,
а две другие составляют вместе прямую
Сумма смежный углов 180 градусов
Из двух смежных углов либо один острый, другой тупой,, либо они оба прямые.
Два угла называются вертикальными, если стороны одного угла , дополняют до
прямых стороны другого угла.
Вертикальные углы равны
Угол
между
биссектрисами смежных углов равен 90°.
На главную

4.

Углы при параллельных прямых
1
2
4 3
180
Биссектрисы внутренних односторонних углов при параллельных прямых и секущей
перпендикулярны
Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба
тупые.
4-2 – внутренние накрестлежащие;
2-3 – внутренние односторонние;
1-4 - соотвественные
Если при пересечении двух прямых третьей образуются
равные внутренние накрест лежащие углы или
равные соответственные углы или
внутренние односторонние углы в сумме дают 180 градусов,
то прямые параллельны.
Если две параллельные прямые пересечь третьей, то
образованные при этом:
внутренние накрест лежащие углы равны,
соответственные углы равны,
внутренние односторонние углы в сумме дают 180 градусов.
На главную

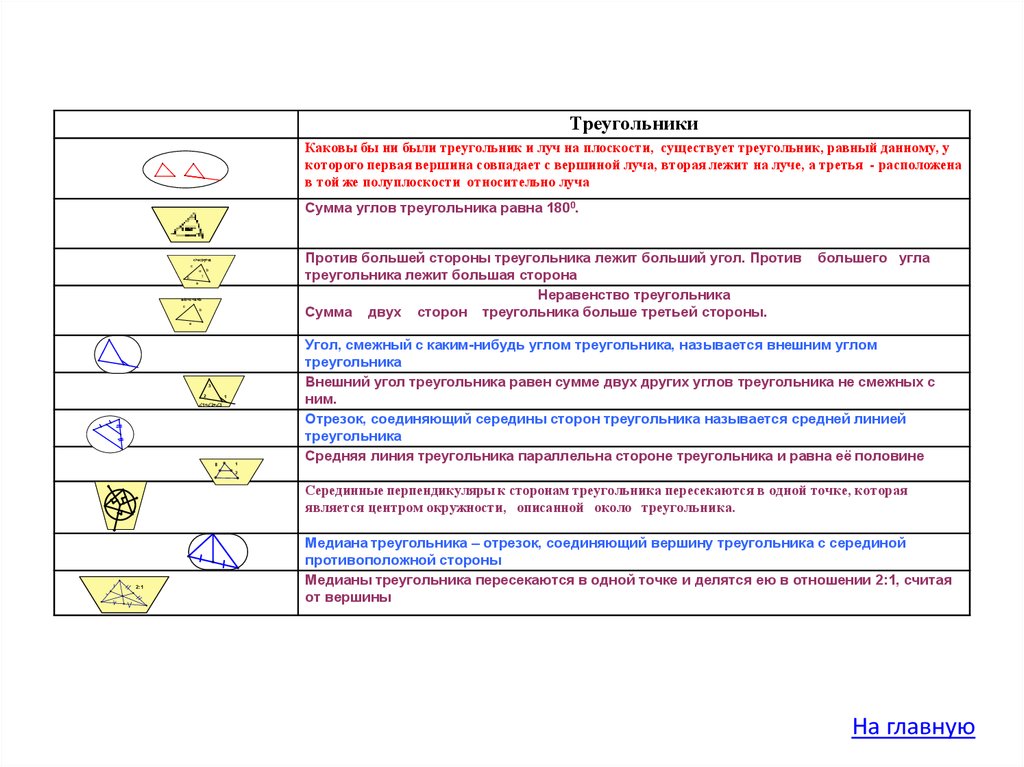
5.

Треугольники
Каковы бы ни были треугольник и луч на плоскости, существует треугольник, равный данному, у
которого первая вершина совпадает с вершиной луча, вторая лежит на луче, а третья - расположена
в той же полуплоскости относительно луча
Сумма углов треугольника равна 1800.
Против большей стороны треугольника лежит больший угол. Против
треугольника лежит большая сторона
Неравенство треугольника
Сумма двух сторон треугольника больше третьей стороны.
c>a >
c
b
a
a-b<c<a+b
c
b
большего угла
a
3
2
1
1= 2+ 3
1
Угол, смежный с каким-нибудь углом треугольника, называется внешним углом
треугольника
Внешний угол треугольника равен сумме двух других углов треугольника не смежных с
ним.
Отрезок, соединяющий середины сторон треугольника называется средней линией
треугольника
Средняя линия треугольника параллельна стороне треугольника и равна её половине
2
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая
является центром окружности, описанной около треугольника.
2:1
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой
противоположной стороны
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая
от вершины
На главную

6.

Треугольники:
биссектрисы, медианы, признаки равенства
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющей
ершину с точкой противолежащей стороны
Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум
другим сторонам
Биссектрисы треугольника пересекаются в одной точке, которая является центром
вписанной в треугольник окружности
x
Если биссектрисы углов В и С треугольника ABC пересекаются в точке М, то ∟
ВМС = 90° + 1/2∟А.
Высота треугольника – отрезок, соединяющий вершину треугольника с точкой
противолежащей стороны или её продолжения и перпендикулярный этой стороне.
Высоты треугольника пересекаются в одной точке. (ортоцентр)
Два треугольника называются равными, если стороны одного соответственно равны
сторонам другого и углы, заключённые между этими сторонами равны
Признаки равенства треугольников.
1.Если две стороны и угол между ними одного треугольника соответственно равны двум
сторонам и углу между ними другого треугольника, то треугольники равны.
2.Если сторона и два прилежащих к ней угла одного треугольника соответственно равны
стороне и двум прилежащим к ней углам другого треугольника, то треугольники
равны.
3.Если три стороны одного треугольника соответственно равны трём сторонам другого
треугольника, то треугольники равны.
На главную

7.

Равнобедренноый треугольник
Равнобедренным называется треугольник, у которого две стороны равны
Если два угла треугольника равны, то он равнобедренный
Углы при основании равнобедренного треугольника равны.
Медиана равнобедренного треугольника, проведенная из его
вершины, является биссектрисой и высотой
Если медиана треугольника является его биссектрисой, то треугольник
равнобедренный.
Медиана равнобедренного треугольника, проведенная из его вершины, является
биссектрисой и высотой
Если медиана треугольника является его высотой, то треугольник равнобедренный.
Медиана равнобедренного треугольника, проведенная из его вершины, является
биссектрисой и высотой.
Если биссектриса треугольника является его высотой, то треугольник равнобедренный
Равнобедренный треугольник симметричен относительно высоты, проведённой к основанию
На главную

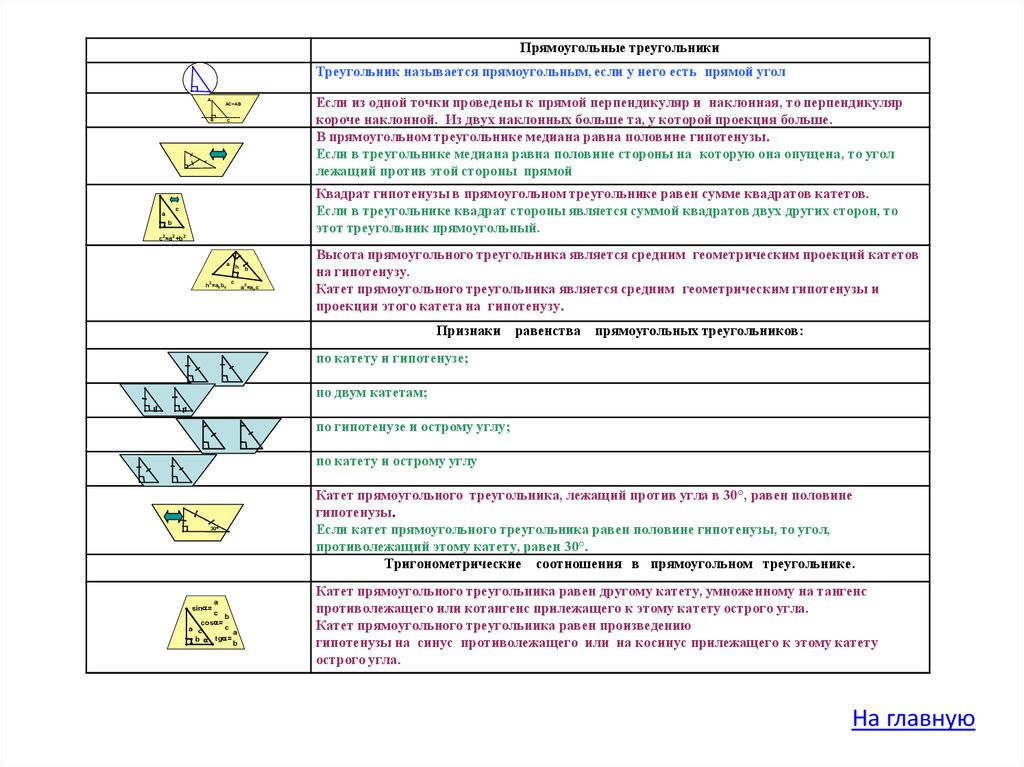
8.

Прямоугольные треугольники
Треугольник называется прямоугольным, если у него есть прямой угол
А
Если из одной точки проведены к прямой перпендикуляр и наклонная, то перпендикуляр
короче наклонной. Из двух наклонных больше та, у которой проекция больше.
В прямоугольном треугольнике медиана равна половине гипотенузы.
Если в треугольнике медиана равна половине стороны на которую она опущена, то угол
лежащий против этой стороны прямой
АС>АВ
В
С
Квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов.
Если в треугольнике квадрат стороны является суммой квадратов двух других сторон, то
этот треугольник прямоугольный.
с
а
b
с2=а2+b2
а
h2=acbc
h
с
b
a2=acc
Высота прямоугольного треугольника является средним геометрическим проекций катетов
на гипотенузу.
Катет прямоугольного треугольника является средним геометрическим гипотенузы и
проекции этого катета на гипотенузу.
Признаки равенства прямоугольных треугольников:
по катету и гипотенузе;
по двум катетам;
по гипотенузе и острому углу;
по катету и острому углу
30
sin =
a
c
b
cos =
c
а с
a
b tg =
b
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине
гипотенузы.
Если катет прямоугольного треугольника равен половине гипотенузы, то угол,
противолежащий этому катету, равен 30°.
Тригонометрические соотношения в прямоугольном треугольнике.
Катет прямоугольного треугольника равен другому катету, умноженному на тангенс
противолежащего или котангенс прилежащего к этому катету острого угла.
Катет прямоугольного треугольника равен произведению
гипотенузы на синус противолежащего или на косинус прилежащего к этому катету
острого угла.
На главную

9.

Признаки подобия треугольников
Подобными называются треугольники, у которых углы равны, а
соответственные стороны пропорциональны.
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключённые между этими
сторонами, равны, то треугольники подобны.
Если два угла одного треугольника соответственно равны двум
углам другого, то треугольники подобны.
Если три стороны одного треугольника соответственно
пропорциональны трём сторонам другого, то треугольники подобны
Теорема синусов
a
b
c
2R
sin sin sin
Теорема косинусов
c 2 a 2 b 2 2ab cos
b
f a
e
c
d
Теорема Менелая
a c e
1
b d f
На главную

10.

Четырёхугольники
Середины сторон любого четырёхугольника являются вершинами параллелограмма.
Параллелограмм
Параллелограммом называется четырёхугольник, противоположные стороны которого
попарно параллельны
Признаки и свойства параллелограмма
Диагональ разбивает параллелограмм на два равных треугольника
ZO
Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот
четырёхугольник -параллелограмм
Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам
Если две противоположные стороны четырёхугольника равны и параллельны, то этот
четырёхугольник — параллелограмм
Противоположные стороны параллелограмма попарно равны
Противоположные углы параллелограмма попарно равны
Если противоположные стороны четырёхугольника попарно равны, то этот
четырёхугольник — параллелограмм
Биссектрисы соседних углов параллелограмма пересекаются под прямым углом
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов сторон
параллелограмма
Ромбом называется четырёхугольник, все стороны которого равны
Признаки и свойства ромба
Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб
Диагонали ромба делят его углы пополам
Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб
Диагонали ромба перпендикулярны
Прямоугольником называется параллелограмм с прямым углом.
Признаки и свойства прямоугольника
Диагонали прямоугольника равны
Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник
Квадратом называется прямоугольник, все стороны которого равны
На главную

11.

Трапеция
Трапецией называется четырёхугольник, две стороны которого параллельны, а две другие – нет.
Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон..
b
Средняя линия трапеции параллельна основаниям и равна их полусумме.
1/2
a
b
-
Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований
1/2
a
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и
середины оснований лежат на одной прямой
Трапеция называется равнобедренной, если её боковые стороны равны
Свойства и признаки равнобедренной трапеции
Если углы при основании трапеции равны, то она равнобедренная
Углы при основании равнобедренной трапеции равны
Если диагонали трапеции равны, то она равнобедренная
Диагонали равнобедренной трапеции равны
b
+ 1/2
a
-
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности
оснований, а проекция диагонали — полусумме оснований
Равнобокая трапеция симметрична относительно отрезка, соединяющего середины оснований.
Если трапеция обладает осью симметрии, то она равнобокая.
На главную

12.

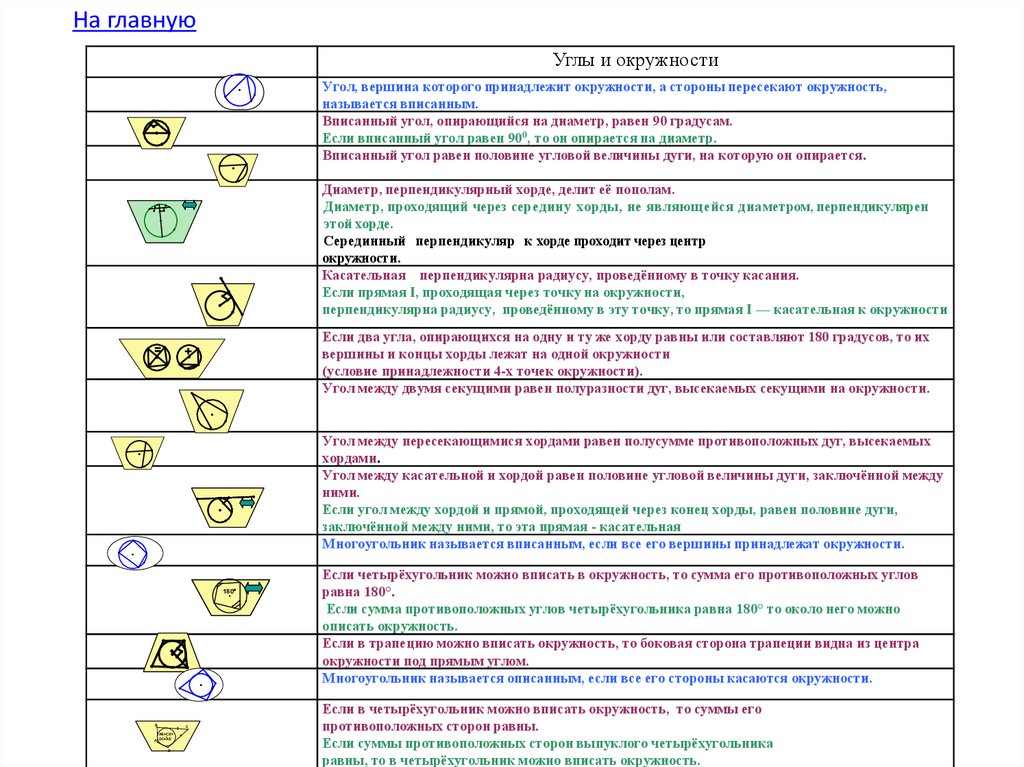
На главную
Углы и окружности
Угол, вершина которого принадлежит окружности, а стороны пересекают окружность,
называется вписанным.
Вписанный угол, опирающийся на диаметр, равен 90 градусам.
Если вписанный угол равен 900, то он опирается на диаметр.
Вписанный угол равен половине угловой величины дуги, на которую он опирается.
Диаметр, перпендикулярный хорде, делит её пополам.
Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен
этой хорде.
Серединный перпендикуляр к хорде проходит через центр
окружности.
Касательная перпендикулярна радиусу, проведённому в точку касания.
Если прямая I, проходящая через точку на окружности,
перпендикулярна радиусу, проведённому в эту точку, то прямая I — касательная к окружности
=
Если два угла, опирающихся на одну и ту же хорду равны или составляют 180 градусов, то их
вершины и концы хорды лежат на одной окружности
(условие принадлежности 4-х точек окружности).
Угол между двумя секущими равен полуразности дуг, высекаемых секущими на окружности.
+
Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых
хордами.
Угол между касательной и хордой равен половине угловой величины дуги, заключённой между
ними.
Если угол между хордой и прямой, проходящей через конец хорды, равен половине дуги,
заключённой между ними, то эта прямая - касательная
Многоугольник называется вписанным, если все его вершины принадлежат окружности.
180
B
C
AB+CD=
A DC+AD
D
Если четырёхугольник можно вписать в окружность, то сумма его противоположных углов
равна 180°.
Если сумма противоположных углов четырёхугольника равна 180° то около него можно
описать окружность.
Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра
окружности под прямым углом.
Многоугольник называется описанным, если все его стороны касаются окружности.
Если в четырёхугольник можно вписать окружность, то суммы его
противоположных сторон равны.
Если суммы противоположных сторон выпуклого четырёхугольника
равны, то в четырёхугольник можно вписать окружность.

13.

Площади
S1
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
S1 2
S 2 =k
S2
Медиана делит треугольник на два равновеликих треугольника
S
S
a
b
a
S1
S2
S1 S
2
a
b
=
S1
S2
b
Отношение площадей треугольников, на которые биссектриса делит данный треугольник равно
отношению сторон, прилежащих к углу, из которого проведена биссектриса.
Отношение площадей треугольников с одинаковой высотой равно отношению оснований.
Произведение основания на высоту для данного треугольника постоянно.
а
1
S= ah
h
b
2
1
S= ab sin
2
Площадь треугольника
Формула Герона
S
1
ah
2
S
S p p a p b p c
Площадь треугольника
S pr
1
ab sin
2
p полупериметр
p полупериметр
Площадь прямоугольного треугольника S
1
ab
2
Площадь параллелограмма
S ah
Площадь параллелограмма
S
S
1
d1d 2 sin
2
Площадь трапеции
S
1
a b h
2
Площадь круга
S r
S
S ab sin
1
d1 d 2 sin
2
1
( a b) h
2
S r 2
2
На главную

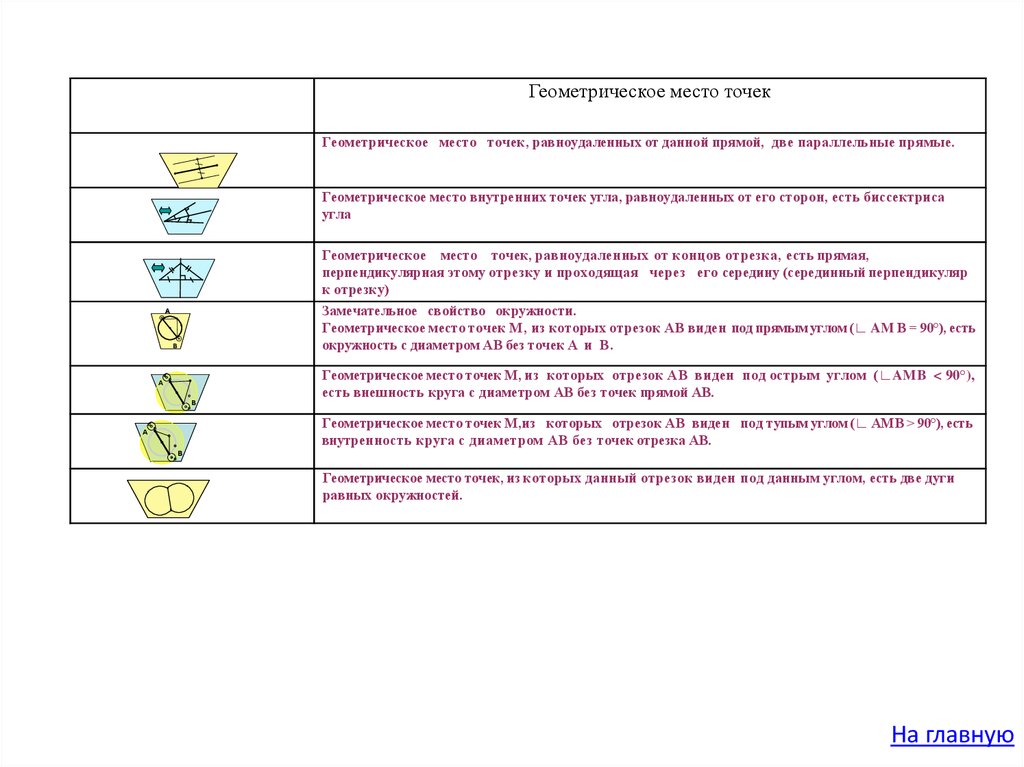
14.

Геометрическое место точек
Геометрическое место точек, равноудаленных от данной прямой, две параллельные прямые.
Геометрическое место внутренних точек угла, равноудаленных от его сторон, есть биссектриса
угла
Геометрическое место точек, равноудаленных от концов отрезка, есть прямая,
перпендикулярная этому отрезку и проходящая через его середину (серединный перпендикуляр
к отрезку)
Замечательное свойство окружности.
Геометрическое место точек М, из которых отрезок АВ виден под прямым углом (∟ AM В = 90°), есть
окружность с диаметром АВ без точек А и В .
A
B
А
В
Геометрическое место точек М, из которых отрезок АВ виден под острым углом (∟AMB < 90°),
есть внешность круга с диаметром АВ без точек прямой АВ.
Геометрическое место точек М,из которых отрезок АВ виден под тупым углом (∟ АМВ > 90°), есть
внутренность круга с диаметром АВ без точек отрезка АВ.
А
В
Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги
равных окружностей.
На главную

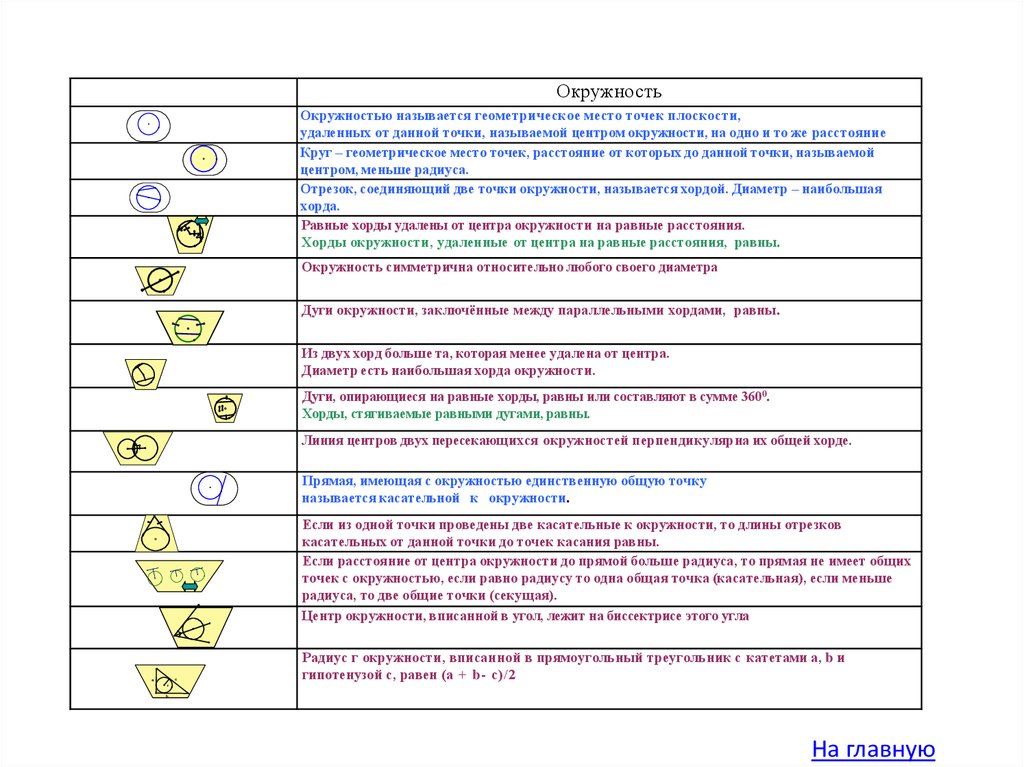
15.

Окружность
Окружностью называется геометрическое место точек плоскости,
удаленных от данной точки, называемой центром окружности, на одно и то же расстояние
Круг – геометрическое место точек, расстояние от которых до данной точки, называемой
центром, меньше радиуса.
Отрезок, соединяющий две точки окружности, называется хордой. Диаметр – наибольшая
хорда.
Равные хорды удалены от центра окружности на равные расстояния.
Хорды окружности, удаленные от центра на равные расстояния, равны.
Окружность симметрична относительно любого своего диаметра
Дуги окружности, заключённые между параллельными хордами, равны.
Из двух хорд больше та, которая менее удалена от центра.
Диаметр есть наибольшая хорда окружности.
Дуги, опирающиеся на равные хорды, равны или составляют в сумме 3600.
Хорды, стягиваемые равными дугами, равны.
Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.
Прямая, имеющая с окружностью единственную общую точку
называется касательной к окружности.
Если из одной точки проведены две касательные к окружности, то длины отрезков
касательных от данной точки до точек касания равны.
Если расстояние от центра окружности до прямой больше радиуса, то прямая не имеет общих
точек с окружностью, если равно радиусу то одна общая точка (касательная), если меньше
радиуса, то две общие точки (секущая).
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла
c
a
Радиус г окружности, вписанной в прямоугольный треугольник с катетами а, b и
гипотенузой с, равен (а + b- с)/2
r
b
На главную

16.

Взаимное расположение окружностей
Даны окружности радиусов г и R (R> г). Расстояние между их центрами равно а (а >
R + г). Тогда отрезки общих внешних и общих внутренних касательных,
заключенные между точками касания, равны соответственно
R
r
a
и
b c a
2
Говорят, что две окружности касаются, если они имеют единственную общую точку (точка касания).
Точка касания двух окружностей лежит на их линии центров
a 2 R r
r
d
2
R
a 2 R r
2
Окружности радиусов г и R с центрами O1 и О2 касаются внешним образом тогда и только тогда,
когда R +r =O1О2
Окружности радиусов г и R (г < R) с центрами О1 и О2 касаются внутренним образом тогда и
только тогда, когда R – r= О1 Ог
В
О1
А
С
К
О2
Окружности с центрами О1 и О2 касаются внешним образом в точке К.
Некоторая прямая касается этих окружностей в различных точках А и В и пересекается с общей
касательной проходящей через точку К, в точке С. Тогда ∟AKB = 90° и ∟ О1 СО2= 90°.
На главную

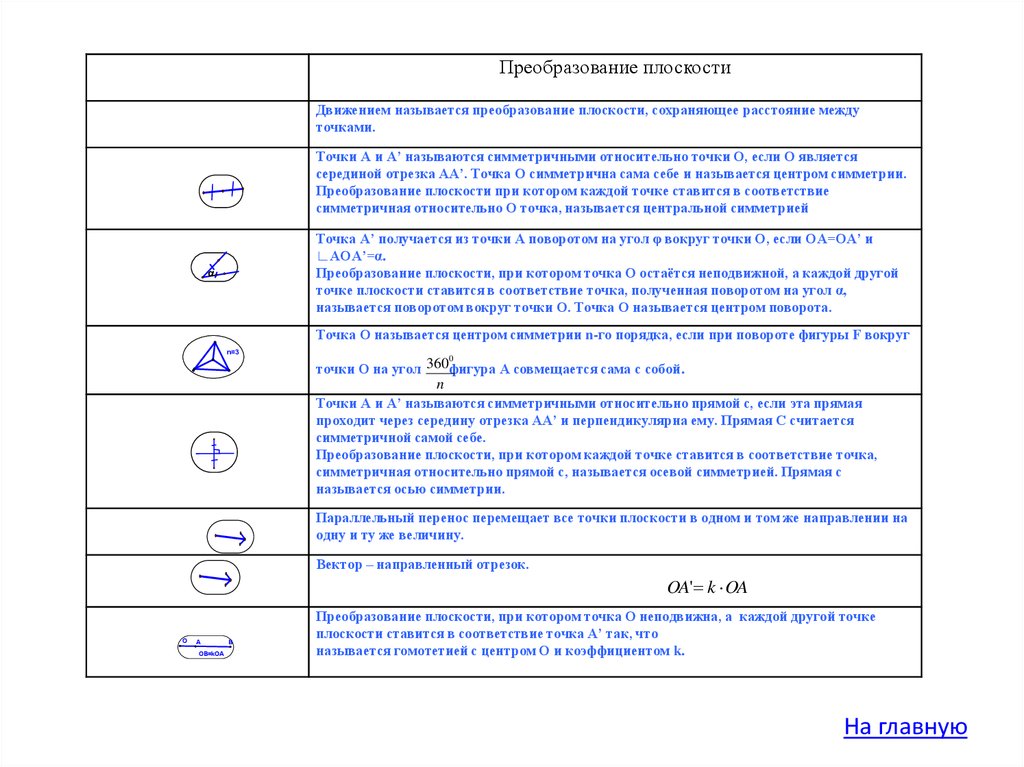
17.

Преобразование плоскости
Движением называется преобразование плоскости, сохраняющее расстояние между
точками.
Точки А и А’ называются симметричными относительно точки О, если О является
серединой отрезка АА’. Точка О симметрична сама себе и называется центром симметрии.
Преобразование плоскости при котором каждой точке ставится в соответствие
симметричная относительно О точка, называется центральной симметрией
Точка А’ получается из точки А поворотом на угол φ вокруг точки О, если ОА=ОА’ и
∟АОА’=α.
Преобразование плоскости, при котором точка О остаётся неподвижной, а каждой другой
точке плоскости ставится в соответствие точка, полученная поворотом на угол α,
называется поворотом вокруг точки О. Точка О называется центром поворота.
Точка О называется центром симметрии n-го порядка, если при повороте фигуры F вокруг
n=3
0
точки О на угол 360 фигура А совмещается сама с собой.
n
Точки А и А’ называются симметричными относительно прямой с, если эта прямая
проходит через середину отрезка АА’ и перпендикулярна ему. Прямая С считается
симметричной самой себе.
Преобразование плоскости, при котором каждой точке ставится в соответствие точка,
симметричная относительно прямой с, называется осевой симметрией. Прямая с
называется осью симметрии.
Параллельный перенос перемещает все точки плоскости в одном и том же направлении на
одну и ту же величину.
Вектор – направленный отрезок.
OA' k OA
О
А
ОВ=kОА
В
Преобразование плоскости, при котором точка О неподвижна, а каждой другой точке
плоскости ставится в соответствие точка А’ так, что
называется гомотетией с центром О и коэффициентом k.
На главную

18.

Треугольник и окружность
B
AM=p-BC
A
M
C
C
A
M AM=p
B
180 -2
B
Если М — точка касания окружности, вписанной в треугольник
ABC со стороной АС, то AM = р - ВС, где р — полупериметр треугольника
Окружность касается стороны ВС треугольника ABC и продолжений сторон АВ и АС. Тогда
расстояние от вершины А до точки касания окружности с прямой АВ равно полупериметру
треугольника ABC
Окружность с центром О, вписанная в треугольник ABC, касается
сторон АВ, ВС и АС соответственно в точках K,L И M. ЕСЛИ ∟KLM = α, то ∟ ВАС = 180° - 2α
c
A
c+b-a
2
a
b
C
В треугольнике со сторонами a, b, c расстояние от вершины А до точек касания вписанной
окружности сторон, содержащих эту вершину, равно
Биссектрисы треугольника пересекаются в одной точке, которая является центром
вписанной окружности.
Точка пересечения серединных перпендикуляров , проведённых к сторонам треугольника
является центром описанной окружности.

19.

x
y
b
a
Пропорциональные отрезки
x
a
b
x
y
b
a
Если из одной точки проведены к окружности касательная и секущая,
то произведение всей секущей на её внешнюю часть равно квадрату
касательной.
Произведение всей секущей на её внешнюю часть для данной точки и
данной окружности постоянно
Произведения отрезков пересекающихся хорд окружностей равны
Теорема Фалеса. Если на одной стороне угла отложить равные отрезки и
через их концы провести параллельные прямые, пересекающие вторую сторону угла, то на второй стороне угла отложатся также равные
отрезки.