Similar presentations:
Степенная функция. 11 класс
1. Степенная функция
Муниципальное бюджетное общеобразовательное учреждение«Средняя общеобразовательная школа №16»
УРОК ПО ТЕМЕ:
Степенная функция
11 класс
Разработка учителя математики
I категории
Илясовой Галины Константиновны
МАЙКОП, 2022 г.
2.
Цели урока: рассмотреть степенную функцию, ее свойства; получить формулы длявычисления производной и первообразной
Задачи урока:
Развивающие:
• дифференциация в обучении,
• развитие навыка самостоятельного отношения поиска решения,
• привитие любви к математике, расширение кругозора учащихся;
Воспитательные:
• развитие коммуникативных умений,
• повышение мотивации к обучению,
• формирование познавательного интереса,
• создание заинтересованности каждого ученика в работе;
Дидактические:
• развитие знаний, умений, навыков учащихся,
• углубление знаний учащихся,
• развитие творческих способностей.
Оборудование: мультимедийный проектор, доска, мел, учебник
3.
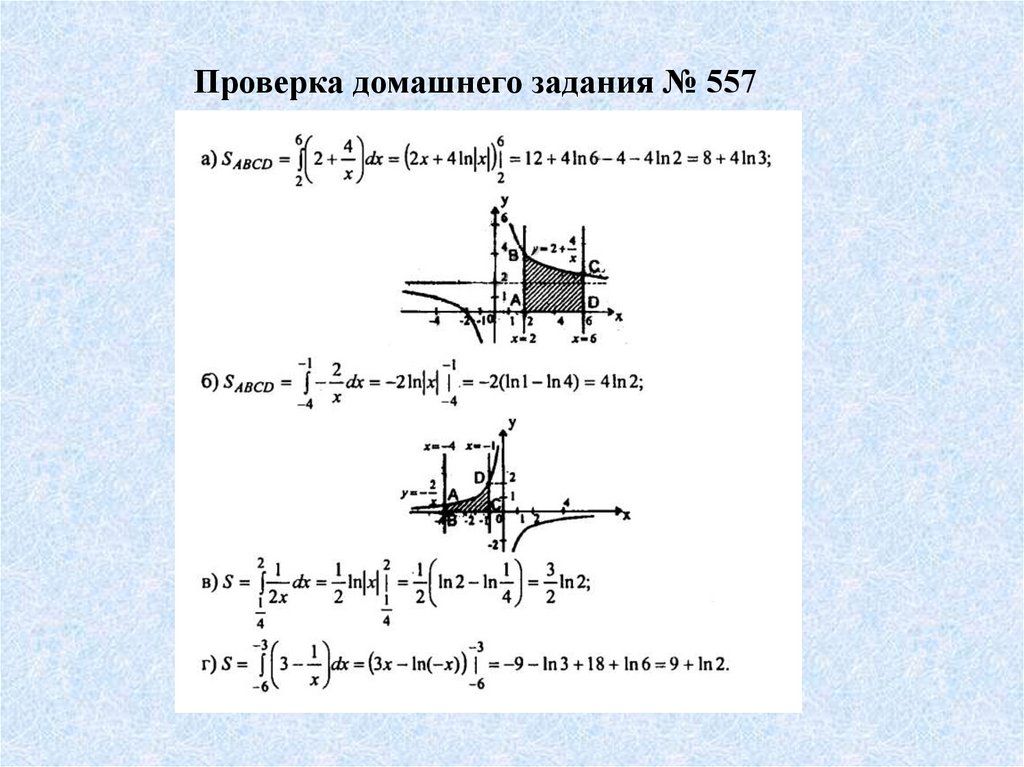
Проверка домашнего задания № 5574.
Самостоятельная работа.Вариант 1
•Найти производную функции
•Найти первообразную функции
•Вычислите площадь фигуры, ограниченной линиями
Вариант 2
•Найти производную функции
•Найти первообразную функции
•Вычислите площадь фигуры, ограниченной линиями
5.
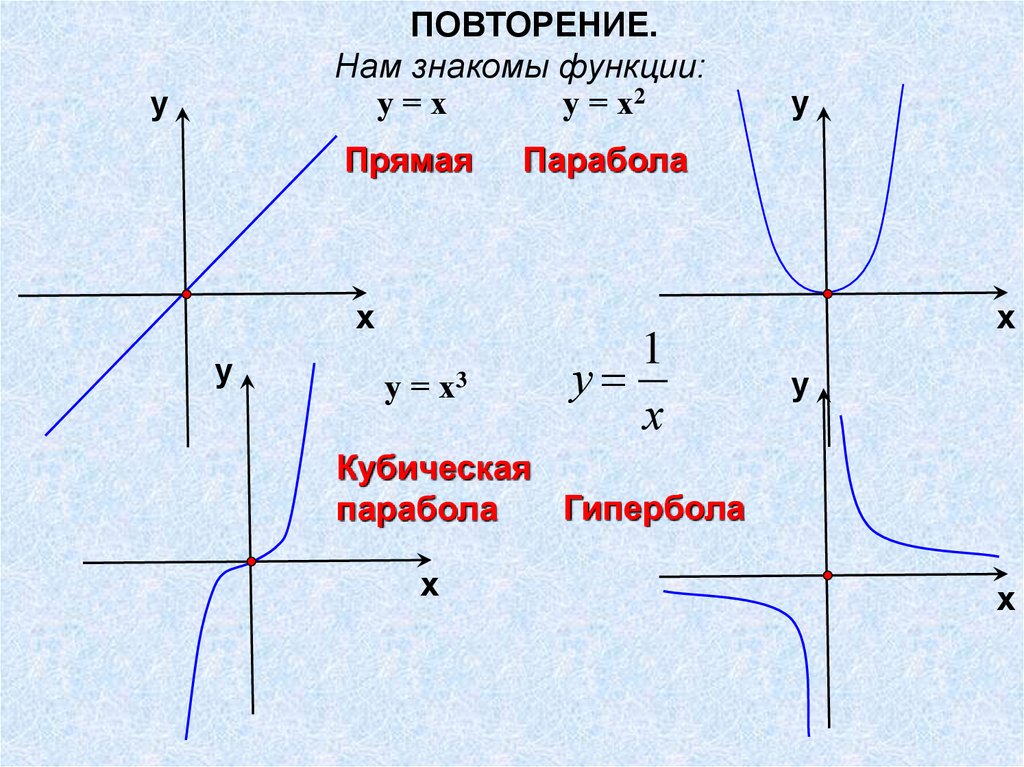
ПОВТОРЕНИЕ.Нам знакомы функции:
у=х
у = х2
у
Прямая
х
у
у = х3
у
Парабола
1
у
х
х
у
Кубическая
Гипербола
парабола
х
х
6.
у = х,у=
х2,
у=
х3,
1
у
х
Все эти функции являются частными
случаями степенной функции
у = хn, у = х-n где n – заданное натуральное число
Свойства и график степенной функции
зависят от значения показателя n
7.
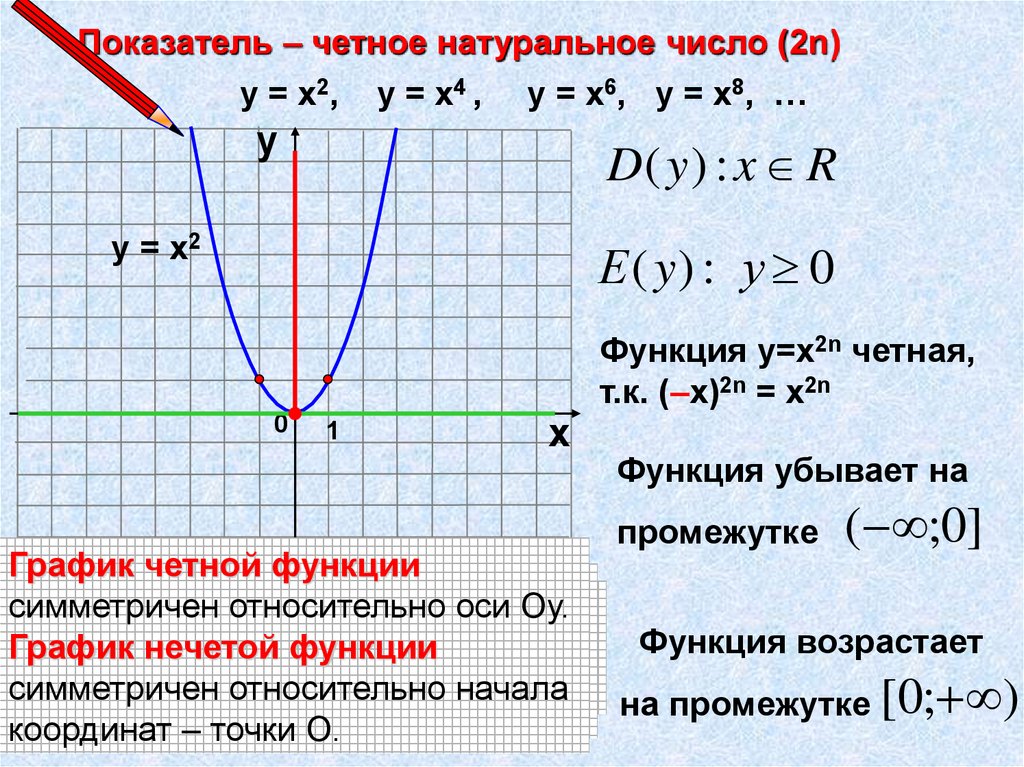
Показатель – четное натуральное число (2n)у = х2, у = х4 , у = х6, у = х8, …
у
D( y ) : x R
у = х2
Е ( y) : у 0
0
1
х
График четной функции
Область определения
значений
функции
симметричен
относительно
оси–Оу.–
Область
функции
множество
значений,
График
нечетой
функции
значения,
которые
может
которые может
принимать
симметричен
относительно
принимать
переменная
х начала
переменная
у О.
координат
– точки
Функция у=х2n четная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
( ;0]
Функция возрастает
на промежутке [0; )
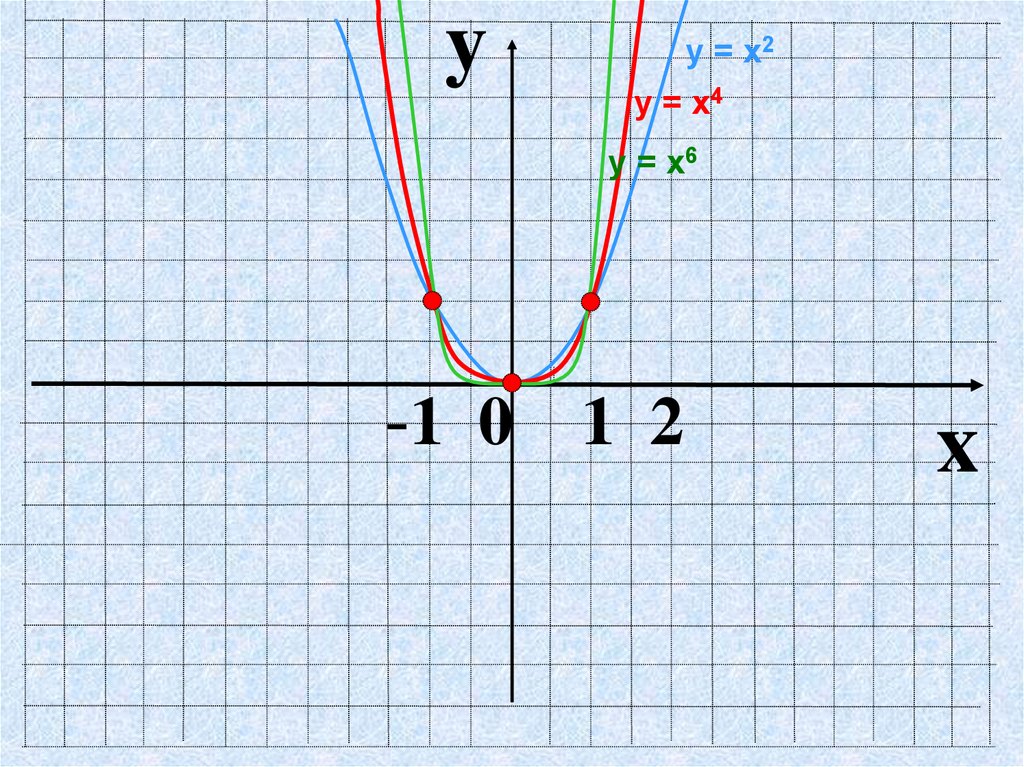
8.
yу = х2
у = х4
у = х6
-1 0 1 2
x
9.
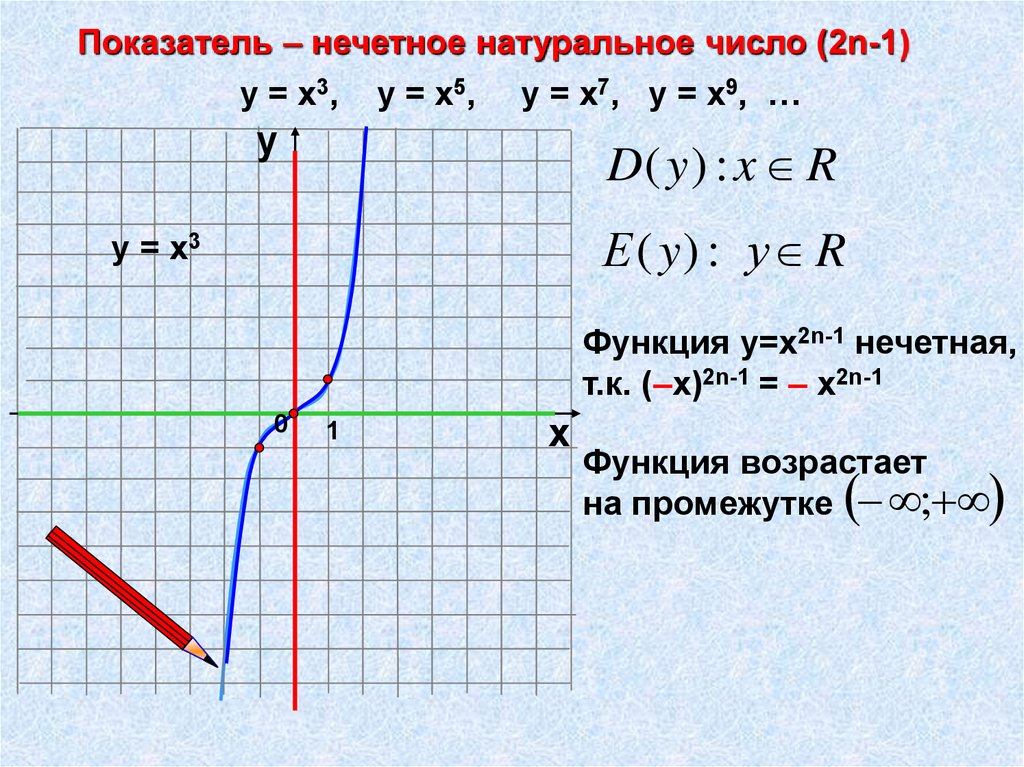
Показатель – нечетное натуральное число (2n-1)у = х3, у = х5, у = х7, у = х9, …
у
D( y ) : x R
Е ( y) : у R
у = х3
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1
0
1
х
Функция возрастает
на промежутке ;
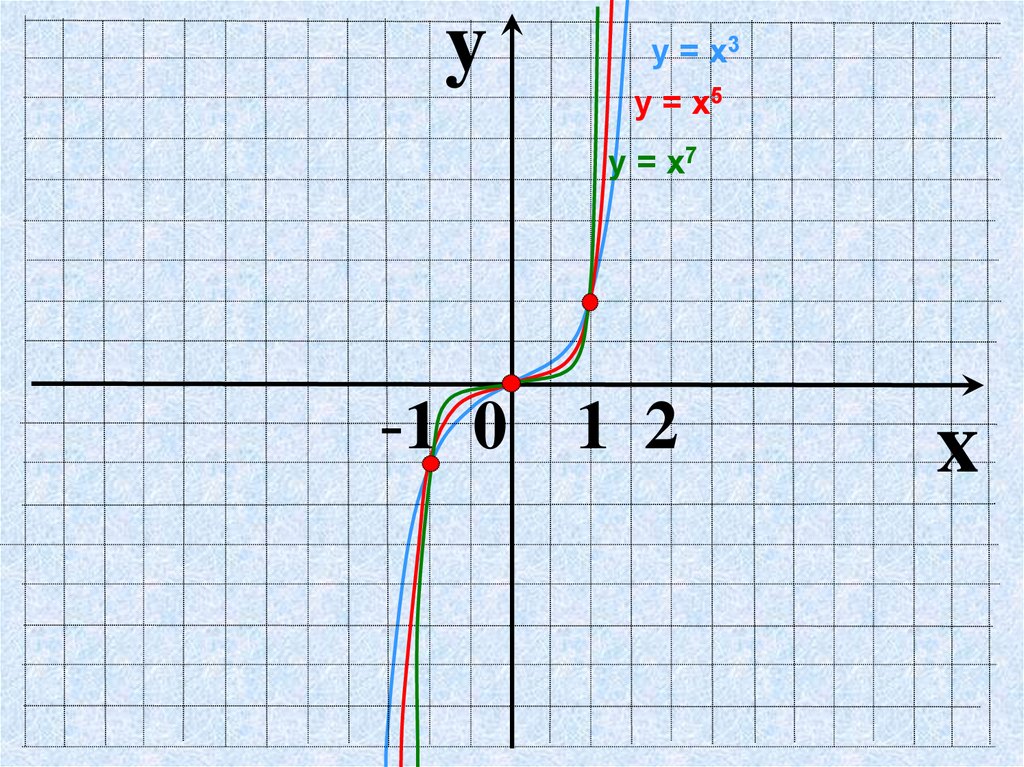
10.
yу = х3
у = х5
у = х7
-1 0 1 2
x
11.
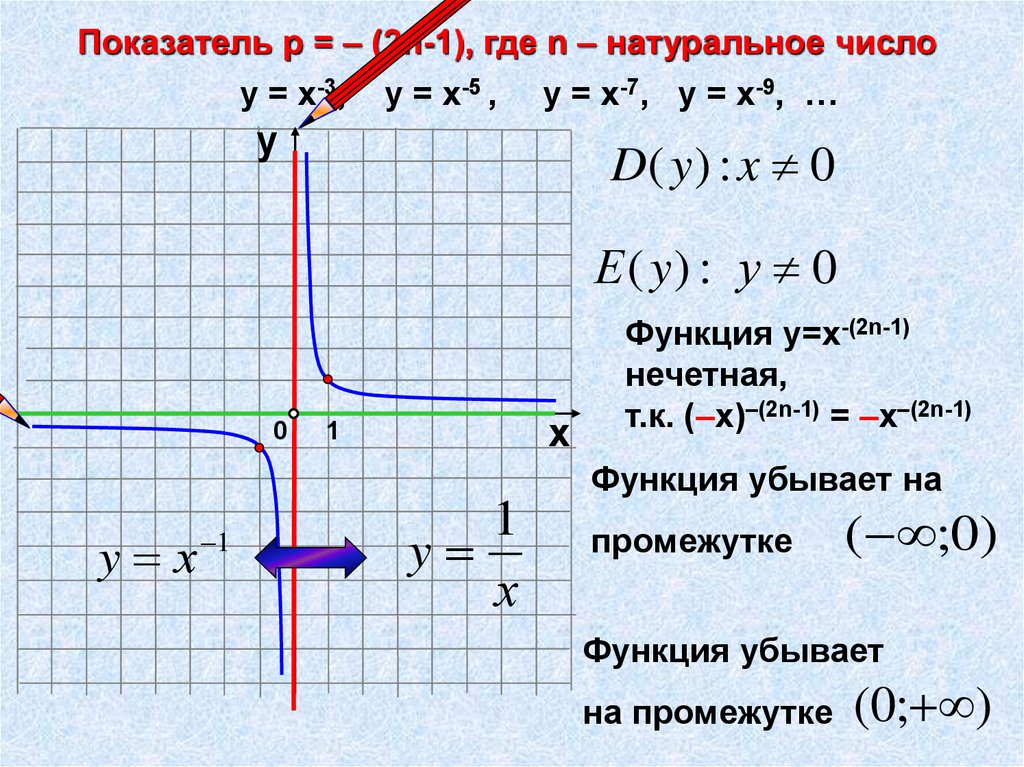
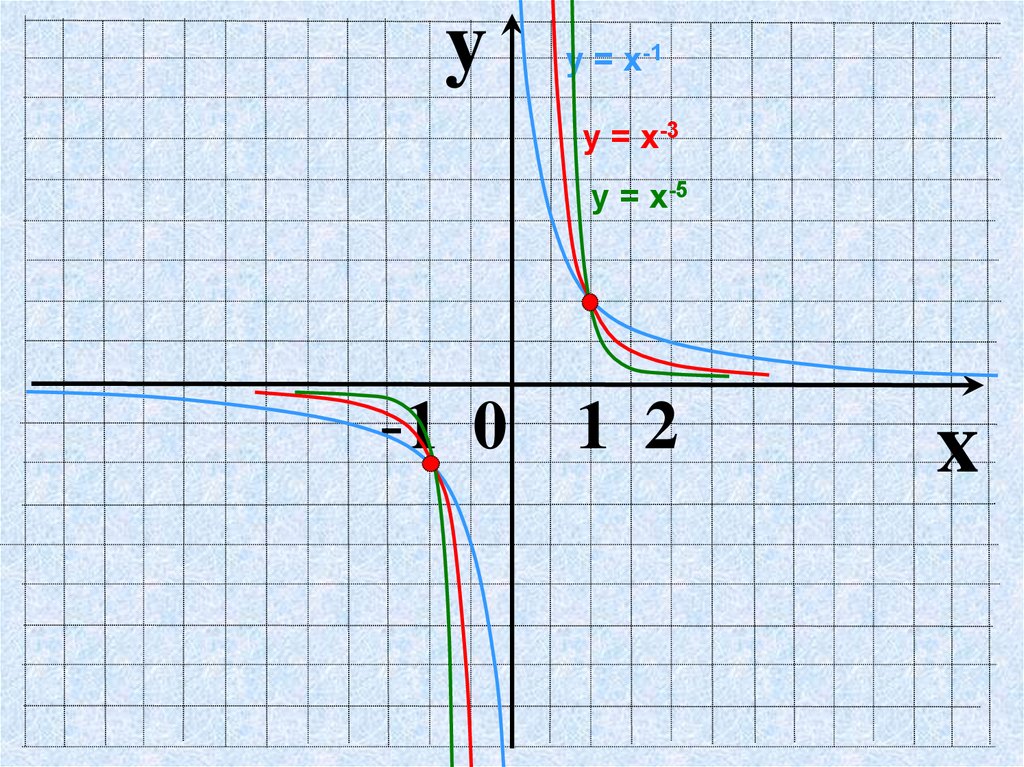
Показатель р = – (2n-1), где n – натуральное числоу = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( y ) : x 0
Е ( y) : у 0
0
х
1
Функция у=х-(2n-1)
нечетная,
т.к. (–х)–(2n-1) = –х–(2n-1)
Функция убывает на
y х
1
1
y
х
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
12.
yу = х-1
у = х-3
у = х-5
-1 0 1 2
x
13.
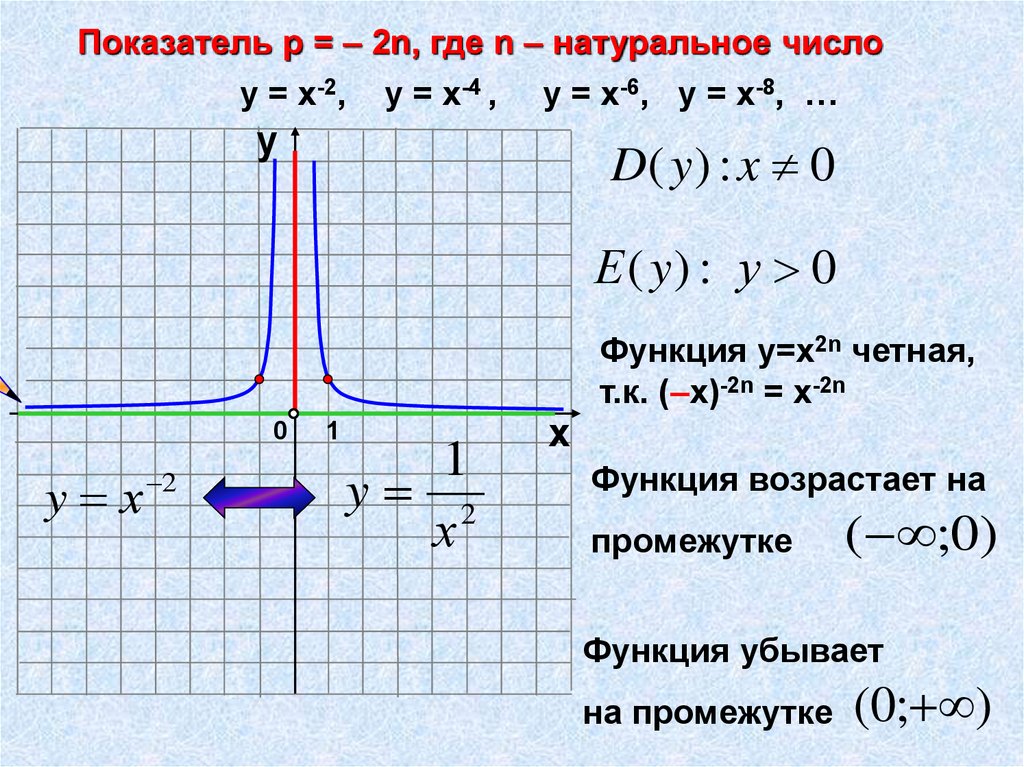
Показатель р = – 2n, где n – натуральное числоу = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
2
1
1
y 2
х
х
Функция у=х2n четная,
т.к. (–х)-2n = х-2n
Функция возрастает на
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
14.
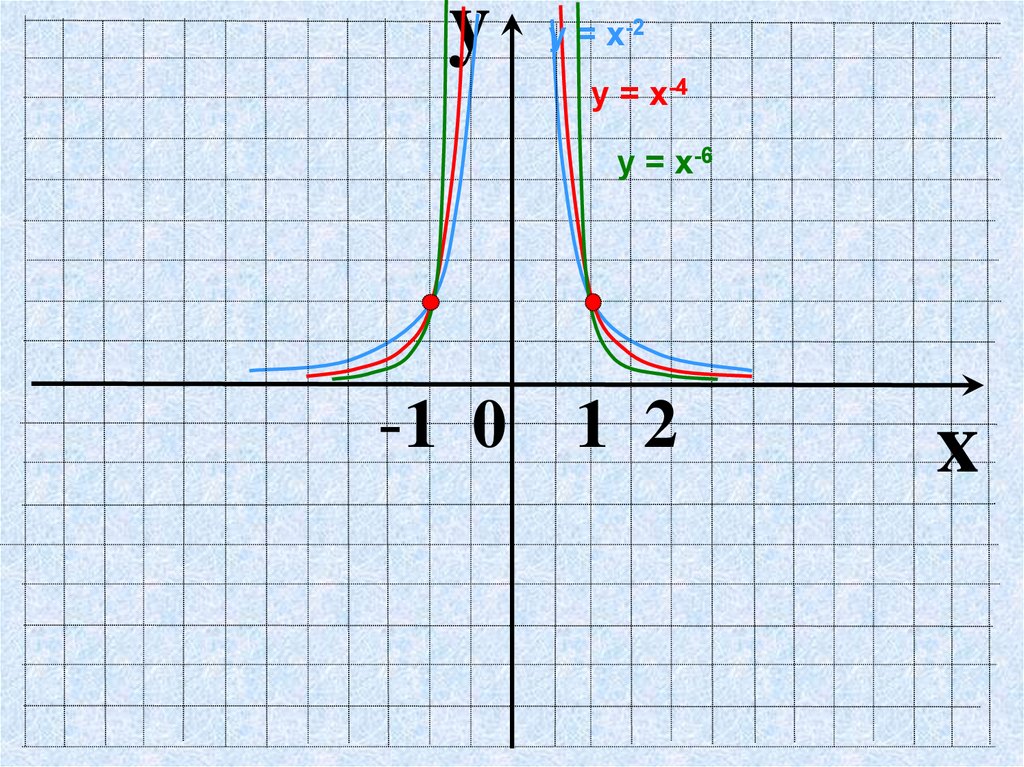
yу = х-2
у = х-4
у = х-6
-1 0 1 2
x
15.
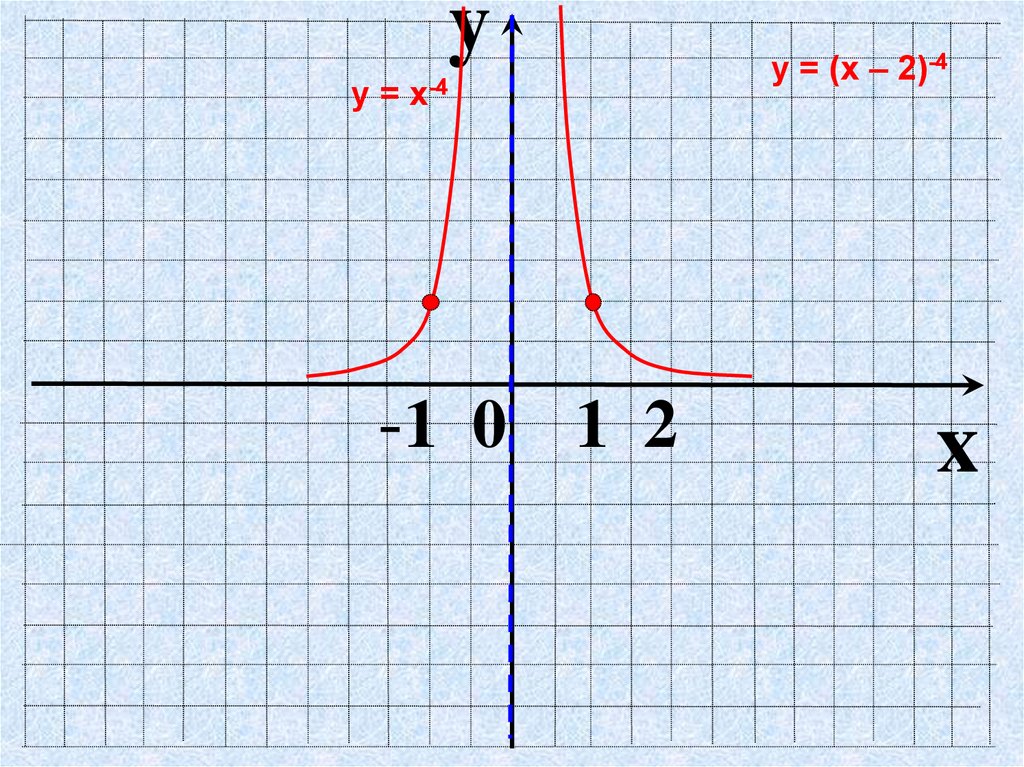
yу = х-4
-1 0 1 2
у = (х – 2)-4
x
16.
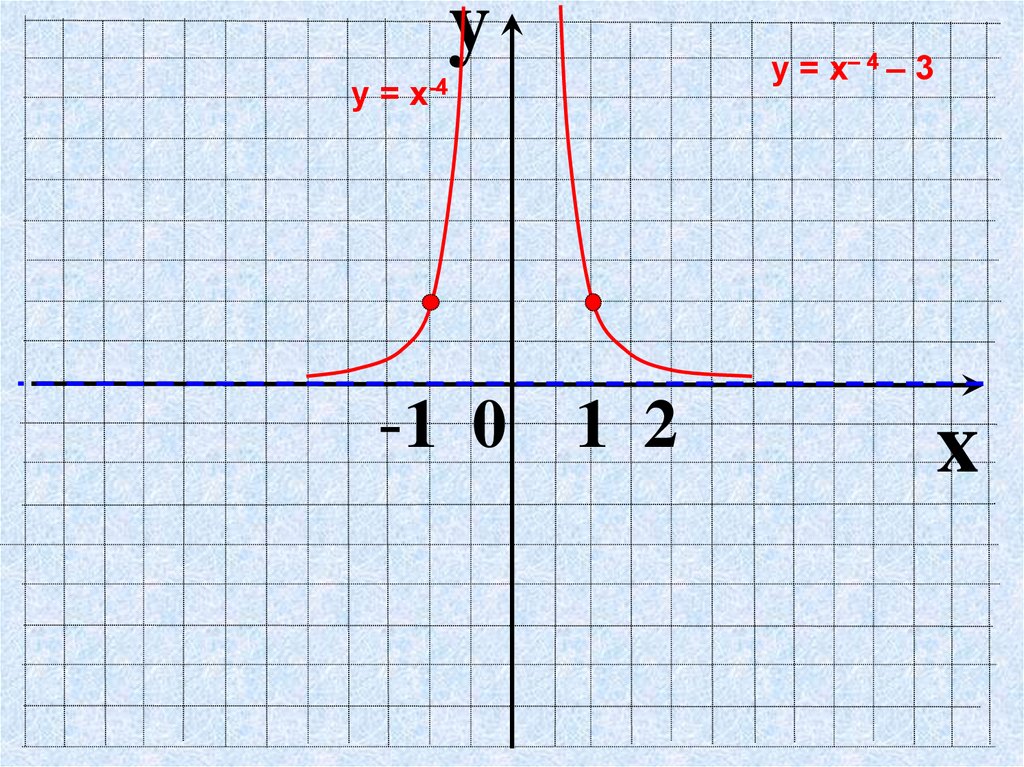
yу = х-4
-1 0 1 2
у = х– 4 – 3
x
17.
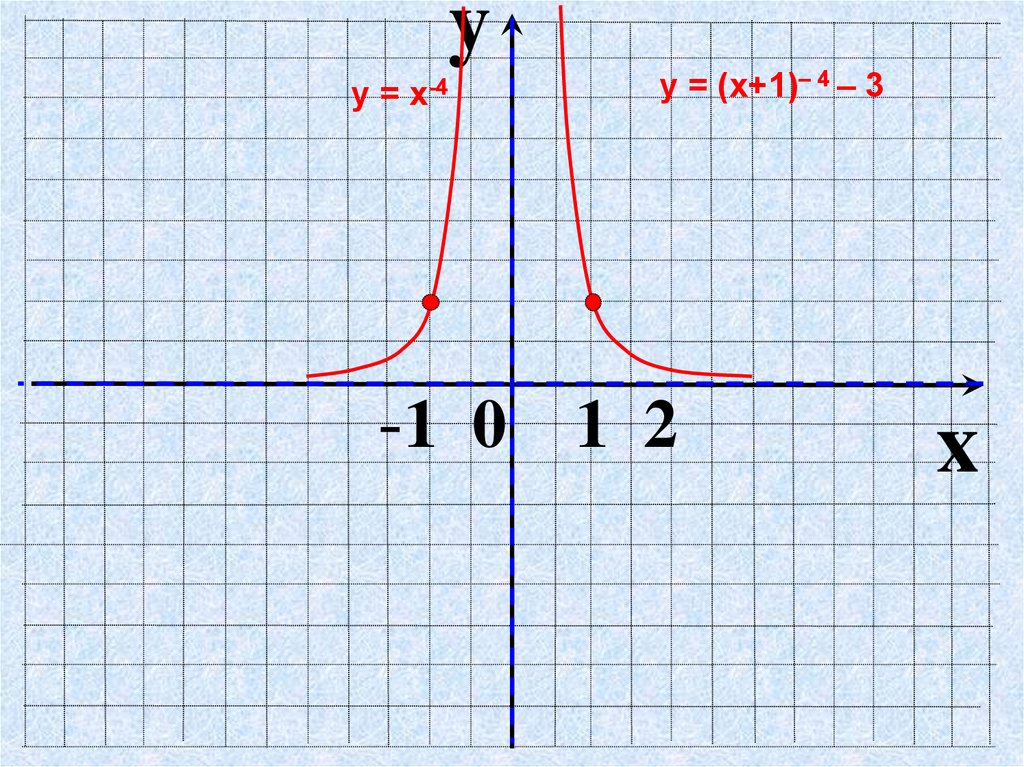
yу = х-4
у = (х+1)– 4 – 3
-1 0 1 2
x
18.
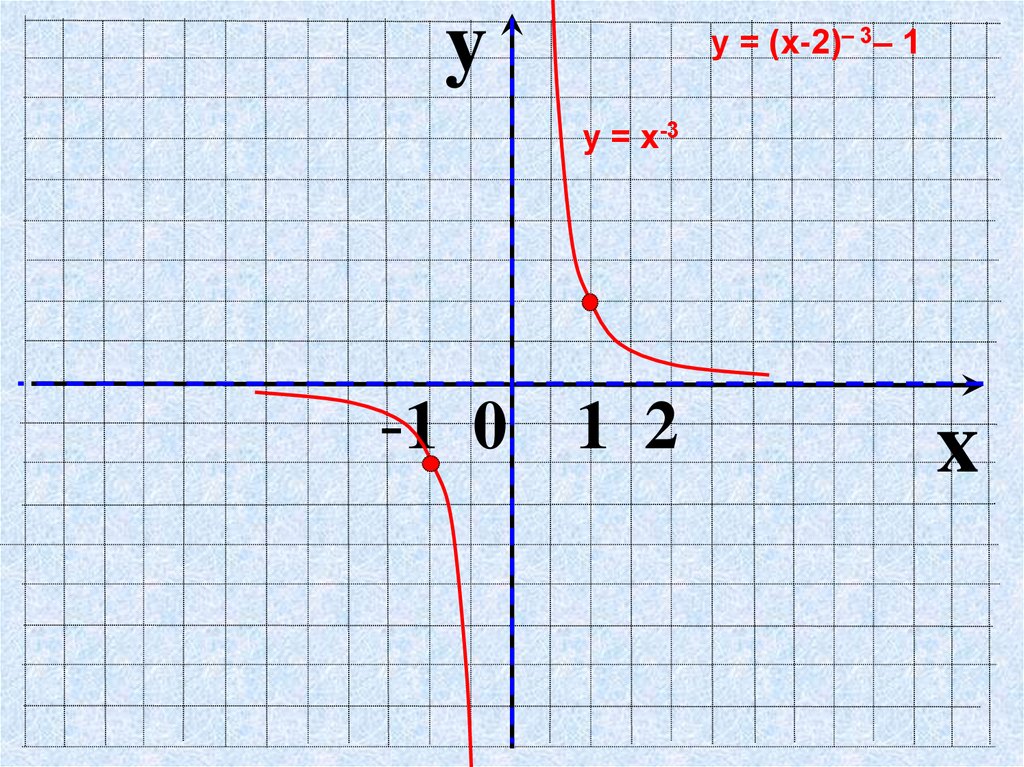
yу = (х-2)– 3– 1
у = х-3
-1 0 1 2
x
19.
Изучение нового материала.Функция, заданная
формулой
называется степенной
( с показателем ).
20.
Если, то степенная
функция определена и при
,
поскольку
.
При целых формулой
степенная функция определена и
для
При четных эта функция чётная, а при
нечетных - нечетная.
Поэтому исследование степенной функции
достаточно провести только на
промежутке (0; ).
21.
Вы знаете формулы дляпроизводной функции
лишь
при целых показателях степени,
а также при
.
Теперь нам остается вывести формулу
при произвольном .
Докажем, что для любого из
области определения производная
степенной функции находится так:
22.
Действительно, так как,
то
Отсюда по правилу вычисления
производной сложной функции получаем:
23.
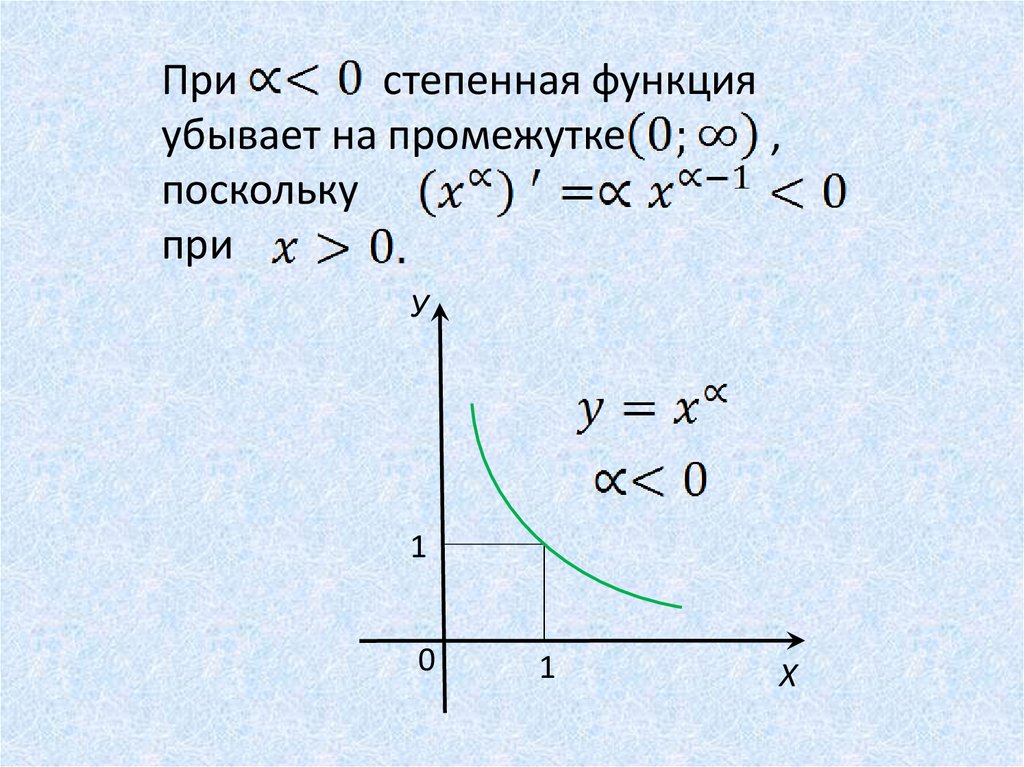
Пристепенная функция
убывает на промежутке
,
поскольку
при
У
1
0
1
Х
24.
Приимеем
,
поэтому степенная функция
возрастает при
.
Кроме того, надо учесть,
что при
степенная функция равна 0 и
при
и
Поэтому точка 0 присоединяется к
промежутку возрастания, т.е. при
степенная функция возрастает на
промежутке [0; ).
25.
УУ
1
1
0
1
Х
0
1
Х
26.
Иначе дело обстоитс первообразной степенной функции.
При
общий вид первообразных
степенной функции
таков:
При
первообразной функции
является функция
27. Практическое применение теории.
Пример 1• Найдем производную функции
• Используем правило дифференцирования сложной функции и формулу
производной степенной функции. Получаем
Пример 2
• Найдем первообразную функции
• Применяя правило интегрирования сложной функции и формулу
первообразной степенной функции, имеем
28.
Решение упражненийУчебник №558(а), 559(а), 560(г), 564(г), 565(в)
Контрольные вопросы
1. Дайте определение степенной функции.
2. Напишите формулу для производной степенной функции.
3. Приведите примеры графиков степенной функции.
4. Напишите формулу для первообразной степенной функции.
Домашнее задание
№558(в), 55(в), 560(а,б), 564(а), 565(а,в)
Подведение итогов урока. Рефлексия.









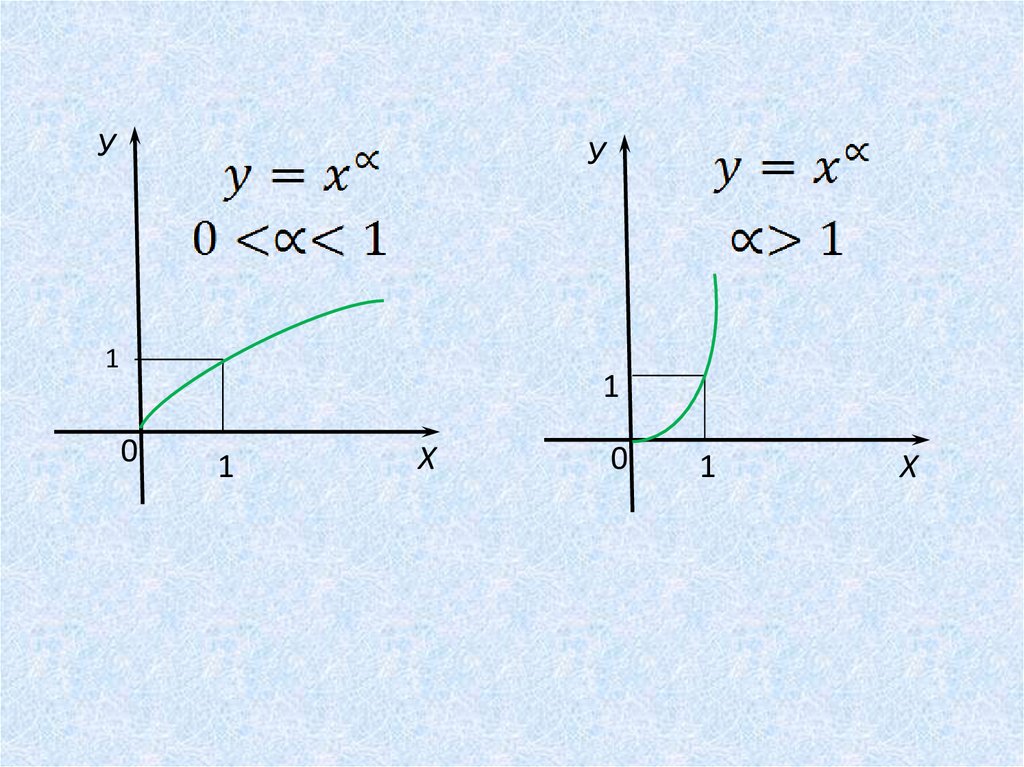



 mathematics
mathematics