Понятие о связанных контурах. Виды связи и коэффициент связи двухконтурной связанной системы

1.

Конспект РТЦиС раздел 05

2.

РАЗДЕЛ 5.
ПОНЯТИЕ О СВЯЗАННЫХ КОНТУРАХ. ВИДЫ СВЯЗИ И
КОЭФФИЦИЕНТ СВЯЗИ ДВУХКОНТУРНОЙ СВЯЗАННОЙ
СИСТЕМЫ
Связанная система - это система, составленная как
минимум из двух колебательных контуров. Контур,
питающийся за счет внешней ЭДС, включенной в его цепь,
называется первичным.
Контур, питающийся за счет ЭДС, наводимой током
первичного контура через элемент связи между контурами,
называется вторичным.
Между контурами имеется элемент связи, называемый
сопротивлением связи Z CB

3.

В зависимости от характера этого сопротивления
различают схемы:
- с трансформаторной,
- автотрансформаторной,
- внутренней емкостной,
- внешней емкостной и другими видами связи.
КОЭФФИЦИЕНТ СВЯЗИ “ К CB ”
“ К CB ” даёт количественную оценку связи между контурами.
Он показывает, какую часть электродвижущая сила, фактически
наведённая во вторичном контуре, составляет от той предельной
величины ЭДС, которую мог бы навести первичный контур во
вторичном.
К СВ
Е2
Е 2 MAX

4.

Коэффициент связи может принимать значения от нуля
до единицы. В радиотехнической аппаратуре применяются
связанные контуры, где коэффициент связи сотые доли
единицы.
Универсальная форма для определения коэффициента
связи К CB
К СВ
Х СВ
Х 1 Х 2
Где
Х CB - сопротивление элемента связи;
Х 1 , Х 2 - реактивные сопротивления
контура, имеющие тоже
характер, что и сопротивление
элемента связи.
(1)

5.

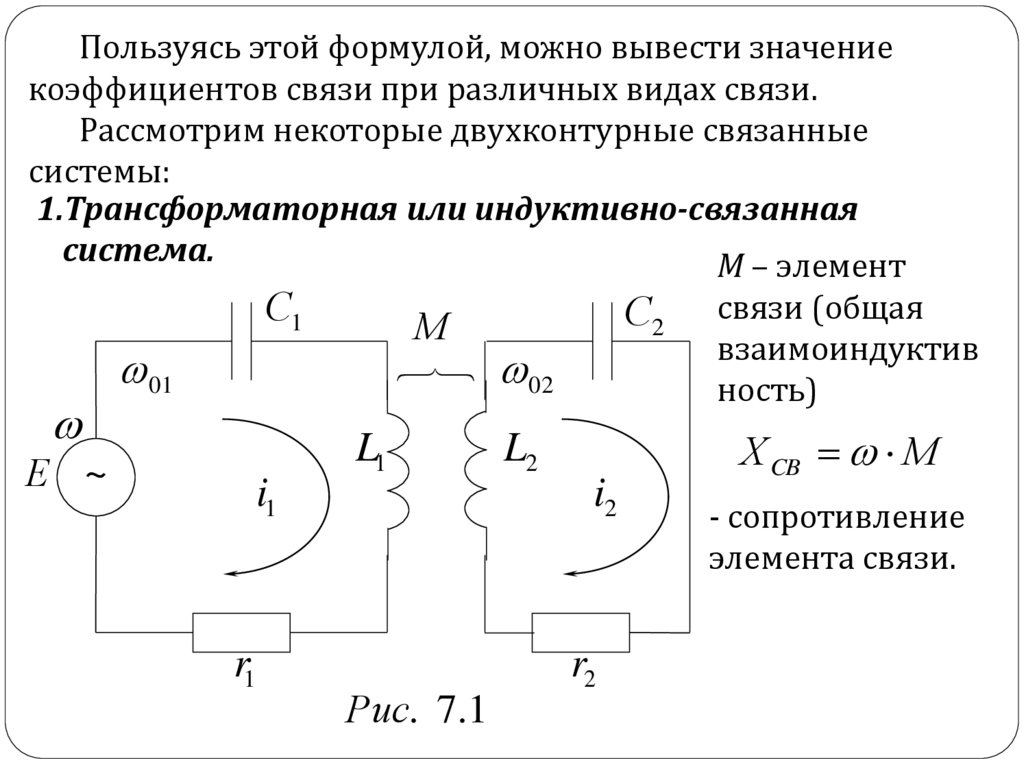
Пользуясь этой формулой, можно вывести значение
коэффициентов связи при различных видах связи.
Рассмотрим некоторые двухконтурные связанные
системы:
1.Трансформаторная или индуктивно-связанная
система.
М – элемент
С1
М
01
L1
Е ~
i1
r1
С2
02
L2
i2
Рис. 7.1
r2
связи (общая
взаимоиндуктив
ность)
Х CB М
- сопротивление
элемента связи.

6.

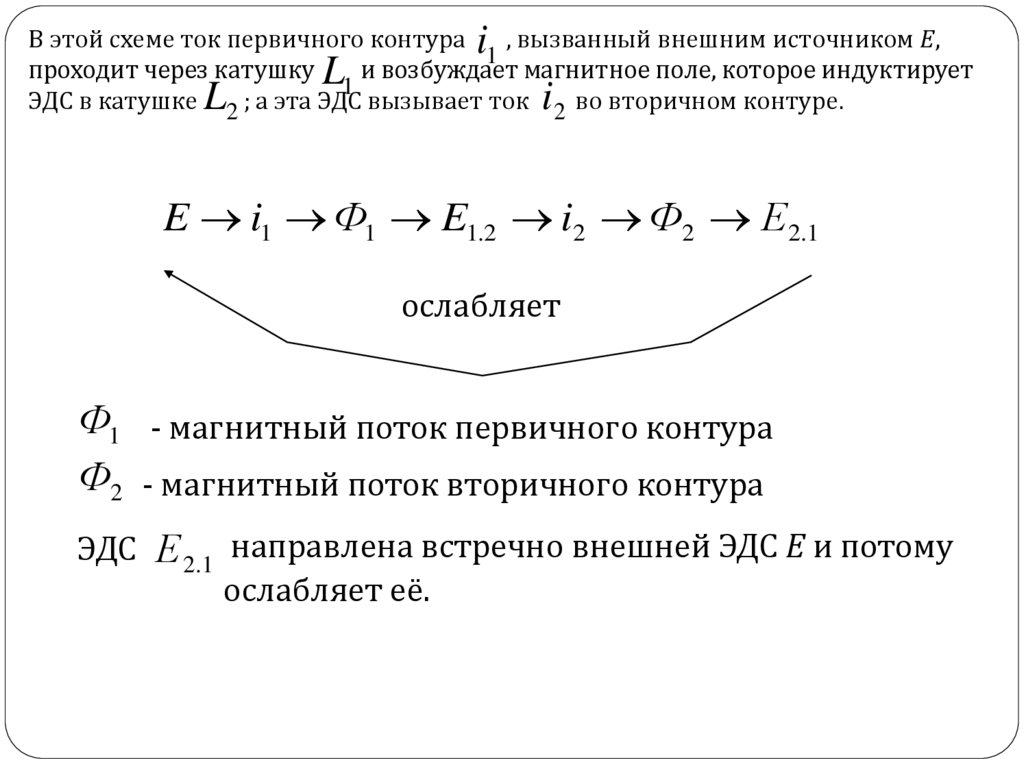
В этой схеме ток первичного контура
, вызванный внешним источником Е,
1
проходит через катушку
и возбуждает магнитное поле, которое индуктирует
1
ЭДС в катушке 2 ; а эта ЭДС вызывает ток 2 во вторичном контуре.
L
L
i
i
E i1 Ф1 E1.2 i2 Ф2 Е2.1
ослабляет
Ф1 - магнитный поток первичного контура
Ф2 - магнитный поток вторичного контура
ЭДС Е 2.1 направлена встречно внешней ЭДС Е и потому
ослабляет её.

7.

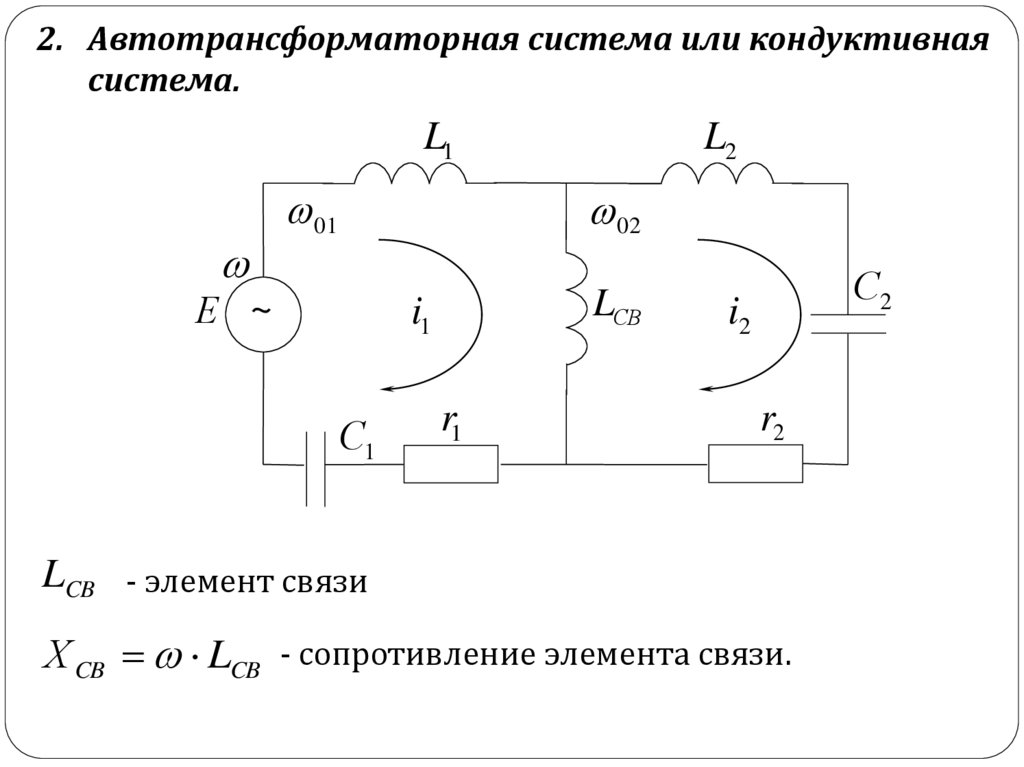
2. Автотрансформаторная система или кондуктивная
система.
L1
01
L2
02
Е ~
LСВ
i1
С1
r1
С2
i2
r2
LCB - элемент связи
Х CB LCB - сопротивление элемента связи.

8.

Ток первичного контура i1 индуктирует ЭДС самоиндукции в
катушке LCB , но т.к. эта катушка общая для обоих контуров,
то во вторичном контуре возникает ЭДС Е1.2 .
E i1 ФСВ ECB1.2 i2 ECB 2.1
ослабляет
ФСВ - магнитный поток охваченный обоими катушками.
ЭДС ЕСВ 2.1 ослабляет внешнюю ЭДС Е т.к. направлена
встречно.

9.

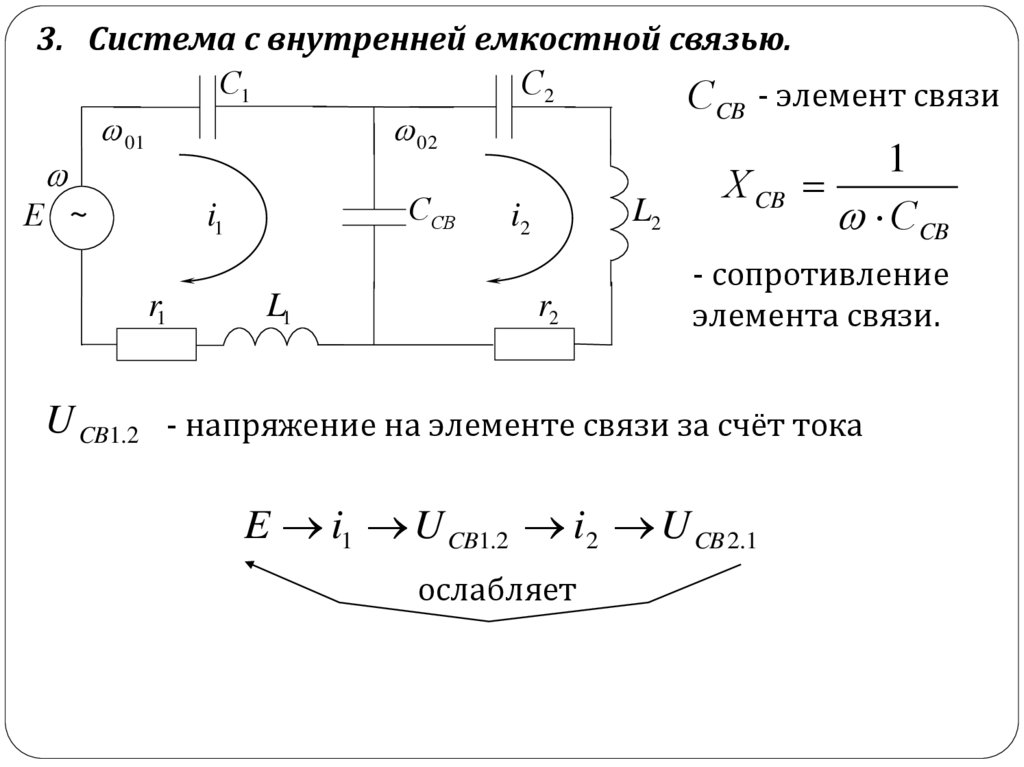
3. Система с внутренней емкостной связью.
С1
С2
С CB - элемент связи
01
02
Е ~
ССВ
i1
r1
L1
L2
i2
r2
1
Х CB
С CB
- сопротивление
элемента связи.
U CB1.2 - напряжение на элементе связи за счёт тока
E i1 U CB1.2 i2 U CB 2.1
ослабляет

10.

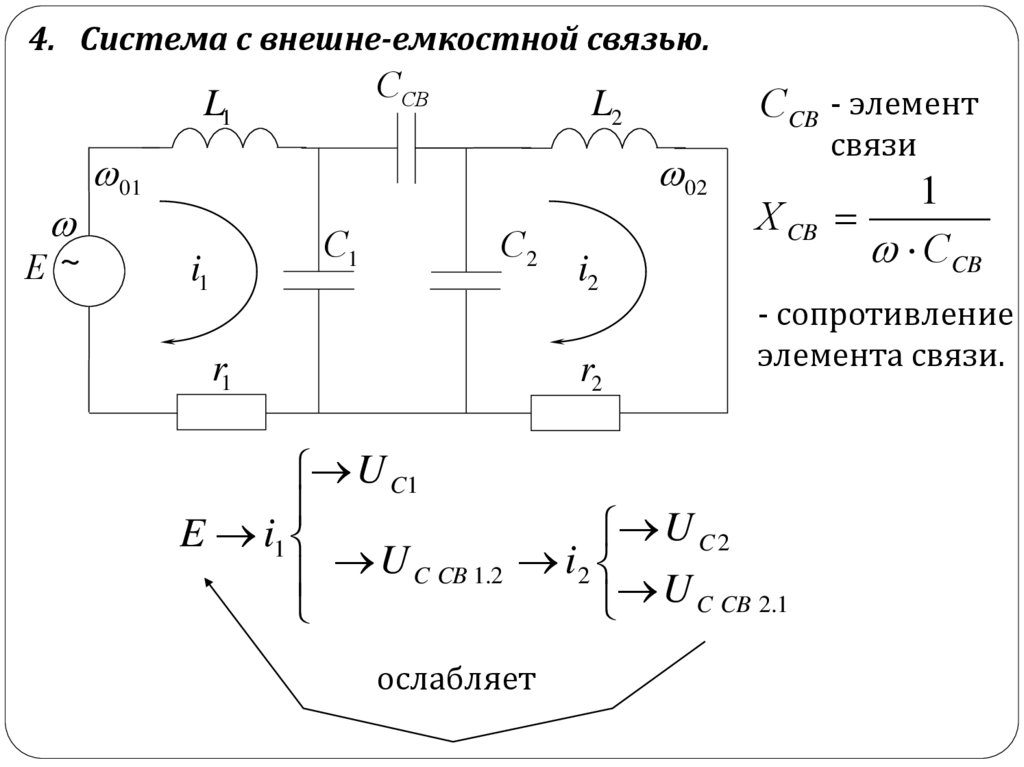
4. Система с внешне-емкостной связью.
ССВ
L1
Е~
С CB - элемент
L2
02
01
С1
i1
С2
r1
i2
r2
связи
1
Х CB
С CB
- сопротивление
элемента связи.
U C1
U C 2
E i1
U
i
C
CB
1
.
2
2
U
C CB 2.1
ослабляет

11.

КОЭФФИЦИЕНТЫ СВЯЗИ В РАЗЛИЧНЫХ 2-Х
КОНТУРНЫХ СИСТЕМАХ
Выражения даны на основе использования универсальной
формулы (1).
1. Для индуктивно-связанной системы:
К СВ
М
L1 L2
(2)
2. Для кондуктивной системы:
К СВ
LCB
( L1 LCB )( L2 LCB )
(3)
3. Для внутренне-емкостной системы:
К СВ
C1 C 2
(C1 C CB )(C 2 C CB )
(4)

12.

4. Для внешне-емкостной системы:
К СВ
C CB
(C1 C CB )(C 2 C CB )
(5)
Задача № 1
Два индуктивно связанных контура имеют М = 2,5 мкГн,
L1 =54мкГн, L2=23мкГн. Определить К CB.
Ответ: К CB =0,07
Задача № 2
Даны два контура с внутренней емкостной связью.
Известны величины емкостей:С1 = С2=25 пФ; С CB=100 пФ.
Определить К CB .
Ответ: К CB =0,2

13.

Задача № 3
Два индуктивно-связанных контура имеют L1 =60мкГн,
L2 =70мкГн, К CB=0,14. Определить М.
Ответ: М = 9,15 мкГн.

14.

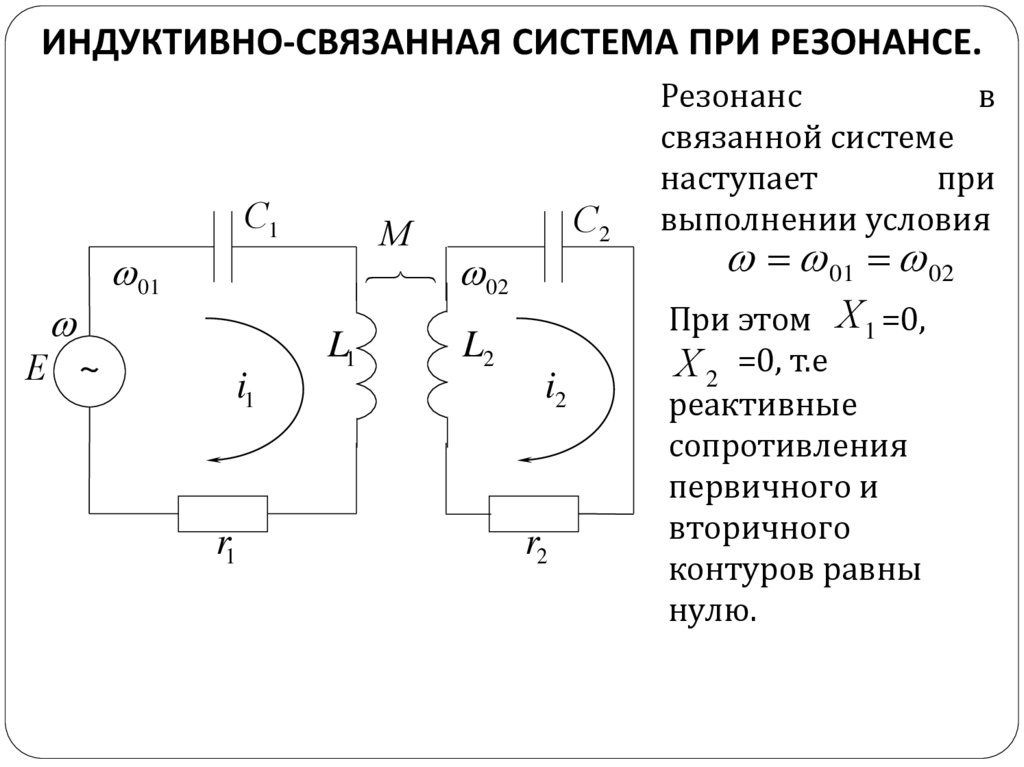
ИНДУКТИВНО-СВЯЗАННАЯ СИСТЕМА ПРИ РЕЗОНАНСЕ.
С1
М
01
L1
Е ~
i1
r1
С2
02
L2
i2
r2
Резонанс
в
связанной системе
наступает
при
выполнении условия
01 02
При этом Х 1 =0,
Х 2 =0, т.е
реактивные
сопротивления
первичного и
вторичного
контуров равны
нулю.

15.

ВЕКТОРНАЯ ДИАГРАММА ПРИ РЕЗОНАНСЕ В
СВЯЗАННОЙ СИСТЕМЕ.
Ф1.2
E 2.1
I1
Е
Е 2.1 - ЭДС первичного
контура
Ф2.1
I2
E1.2
ЕРЕЗ Е Е2.1
Из векторной диаграммы видно,
что Е
ЭДС является
2 .1
противо-ЭДС для внешнего
источника Е , т.е. ослабляет
результирующую ЭДС.
Ф1.2 и Ф-2.магнитный
1
поток

16.

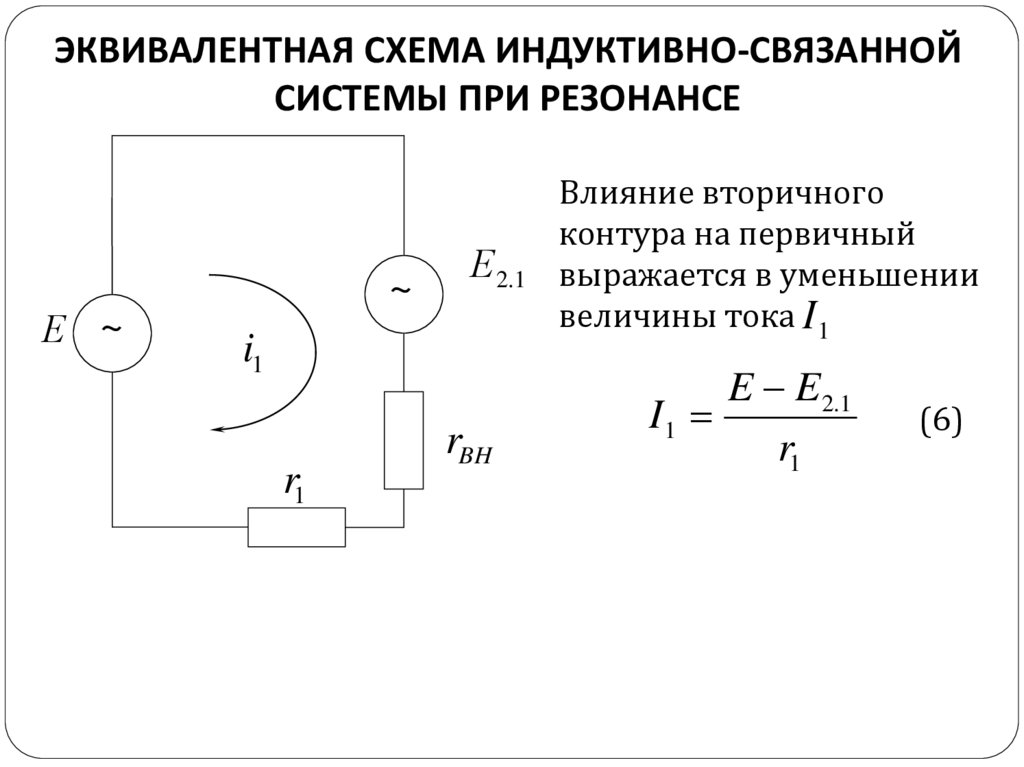
ЭКВИВАЛЕНТНАЯ СХЕМА ИНДУКТИВНО-СВЯЗАННОЙ
СИСТЕМЫ ПРИ РЕЗОНАНСЕ
Е ~
~
Е 2 .1
i1
r1
rBH
Влияние вторичного
контура на первичный
выражается в уменьшении
величины тока I 1
E E 2.1
I1
r1
(6)

17.

Уменьшения тока I 1 в первичном контуре можно
достигнуть не только за счёт включения в первичную цепь
противо-ЭДС Е 2.1 , но и за счёт увеличения сопротивления
активных потерь.
Формула (6) в этом случае будет видоизменена следующим
образом:
E
I1
r1 r BH
(7)
Дополнительное сопротивление активных
“внесённое” в первичный контур обозначим:
rBH - вносимое сопротивление.
потерь,
На основании выражения (7) составим новую
эквивалентную схему индуктивно-связанной системы:

18.

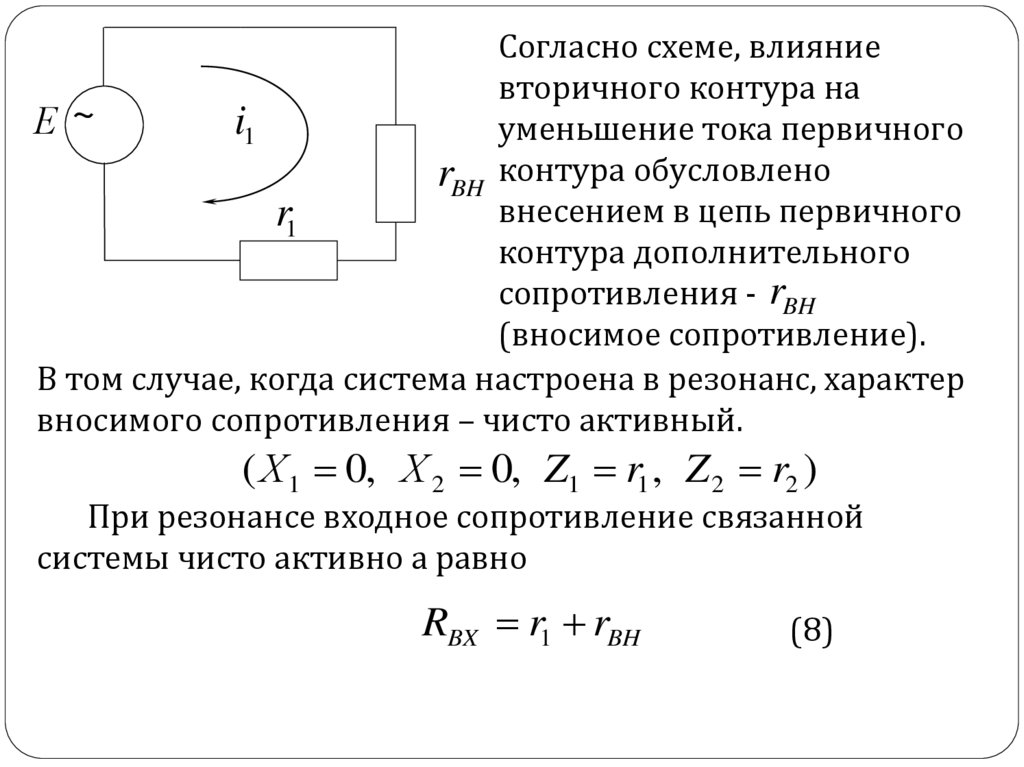
Согласно схеме, влияние
вторичного контура на
Е~
i1
уменьшение тока первичного
rBH контура обусловлено
внесением в цепь первичного
r1
контура дополнительного
сопротивления - rBH
(вносимое сопротивление).
В том случае, когда система настроена в резонанс, характер
вносимого сопротивления – чисто активный.
( Х 1 0, Х 2 0, Z1 r1 , Z 2 r2 )
При резонансе входное сопротивление связанной
системы чисто активно а равно
RBX r1 rBH
(8)

19.

ВЫВЕДЕМ ВЕЛИЧИНУ rBH ПРИ РЕЗОНАНСЕ:
rBH -
вносимое
сопротивление.
Символическое
сопротивление, учитывающее влияние вторичного контура
на первичный, в результате которого ток первичного
контура уменьшается.
Осуществим переход от выражения (6) к выражению (7):
E E2.1
E
I1
I1
r1
r1 rBH
Выразим ЭДС Е 2.1 через параметры вторичного контура
Е 2.1 I 2 X CB ,где
X CB 0 M
E1.2
I 2
r2
E I M
1
0
1.2
(9) (10)
(11)

20.

Тогда, подставив (10), (11) в выражение (9) получим:
E1.2
I 1 ( 0 M ) 2
E 2.1
0 M
r2
r2
Подставим это выражение для Е 2.1 в (6)
I 1 ( 0 M ) 2
E
r2
I1
r1

21.

Преобразуем, получим:
I 1 ( 0 M ) 2
I 1 r1 E
r2
( 0 M ) 2
E
I 1 r1
r2
E
I1
,
2
( 0 M )
r1
r2
Следовательно
( 0 M )
rBH
r2
2
(12)

22.

Для связанной системы с любым видом связи вносимое
сопротивление определяется по формуле:
2
X CB
rBH
Z 20
(13)
если система настроена в резонанс, т.е. 01 02

23.

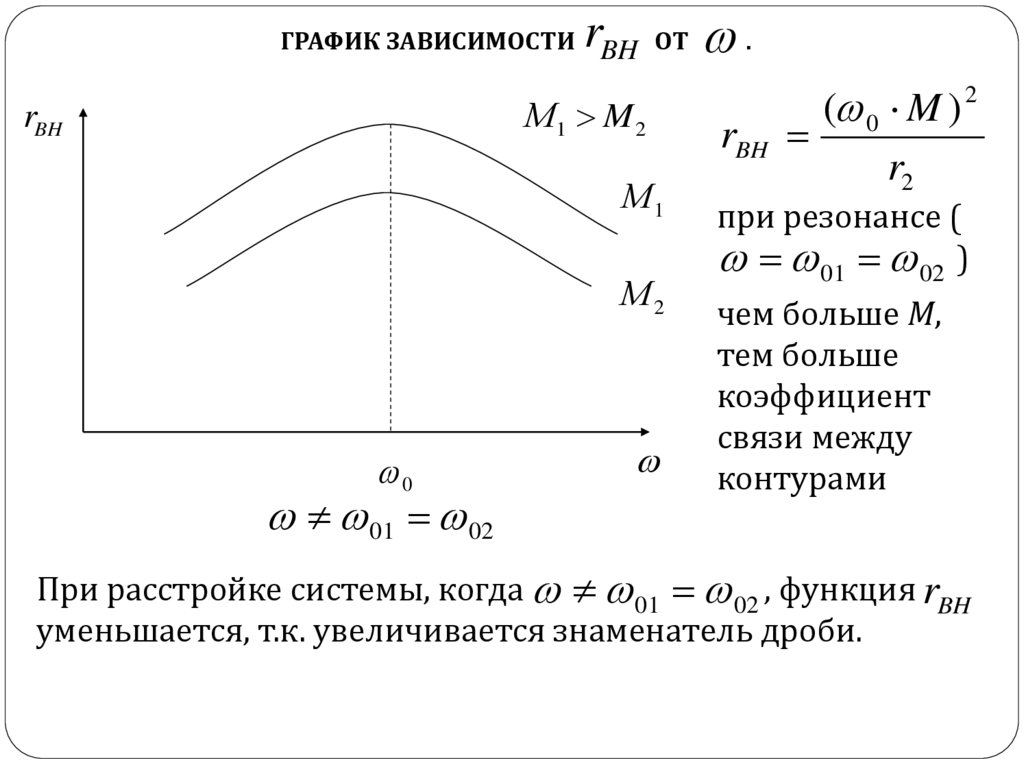
r
ГРАФИК ЗАВИСИМОСТИ BH ОТ
М1 M 2
rBH
М1
М2
0
01 02
.
( 0 M ) 2
rBH
r2
при резонансе (
01 02 )
чем больше М,
тем больше
коэффициент
связи между
контурами
При расстройке системы, когда 01 02 , функция rBH
уменьшается, т.к. увеличивается знаменатель дроби.

24.

ВЫВОД ВЕЛИЧИНЫ Z BH .
Частный случай – выражение (12) можно получить из общего
выражения (21) для вносимого сопротивления на любой
частоте.
Для этого рассмотрим входное сопротивление
связанной системы.
ЭДС Е расходуется на полном сопротивлении первичного
контура Z 1 от тока I 1 и на сопротивлении связи X CB от тока
I2 .
По второму закону Кирхгофа:
E1 I 1 r1 I 2 X CB
(14)
X CB
I 2 I1
Z2
(15)
Во вторичном контуре согласно закону Кирхгофа
0 I1 X CB I 2 Z 2 , откуда

25.

Сделаем подстановку (15) в (14), получим:
2
X CB
E1 I 1 Z1
Z2
Выражение в скобках определяет входное сопротивление
сделанных контуров
2
CB
X
Z BX Z1
Z2
В (16) делаем подстановку
Z 1 r1 jX 1
Z 2 r2 jX 2
X CB jX CB
(16)

26.

Тогда:
2
2
X CB
( jX CB ) 2
X CB
Z BX Z1
r1 jX 1
r1 jX 1
Z2
r2 jX 2
r2 jX 2
Выделим активную RBX и реактивную X BX составляющие
Z BX . Для этого освободимся от мнимого члена в
r2 jX 2
знаменателе дроби, умножив Z BX на
r2 jX 2
2
2
X CB
X CB
Z BX r1 jX1 2
r2 j 2
X2
2
2
r2 X 2
r2 X 2
2
2
X CB
X CB
r1 2 r2 j X 1 2 X 2
Z2
Z2

27.

Где Z 2 - модуль полного сопротивления вторичного контура
Z 2 r22 X 22
Z r X
2
2
2
2
2
2
Активная составляющая Z BX
2
X CB
RBX r1 2 r2
Z2
Реактивная составляющая Z BX
2
CB
2
2
X
Х BX Х 1
Z
без второго контура
RBX r1
X BX X 1
Х2
(17)
(18)

28.

Следовательно, вторые слагаемые из выражения (17) и
(18) обусловлены влиянием вторичного контура, поэтому
они
называются
вносимыми
сопротивлениями
из
вторичного контура в первичный
RBX r1 rBH
(19)
X BX X 1 X BH
(20)
Сопоставив выражения (19), (20) с выражениями (17) и
(18), можно записать
2
X CB
rBH 2 r2
Z2
2
X CB
X BH 2 X 2
Z2
(21)
(22)

29.

Где:
rBH - активная составляющая вносимого сопротивления;
X BH - реактивная составляющая вносимого
сопротивления.
Знак (-) в (22) указывает на то, что активное вносимое
сопротивление противоположно по знаку реактивному
сопротивлению вторичного контура.

30.

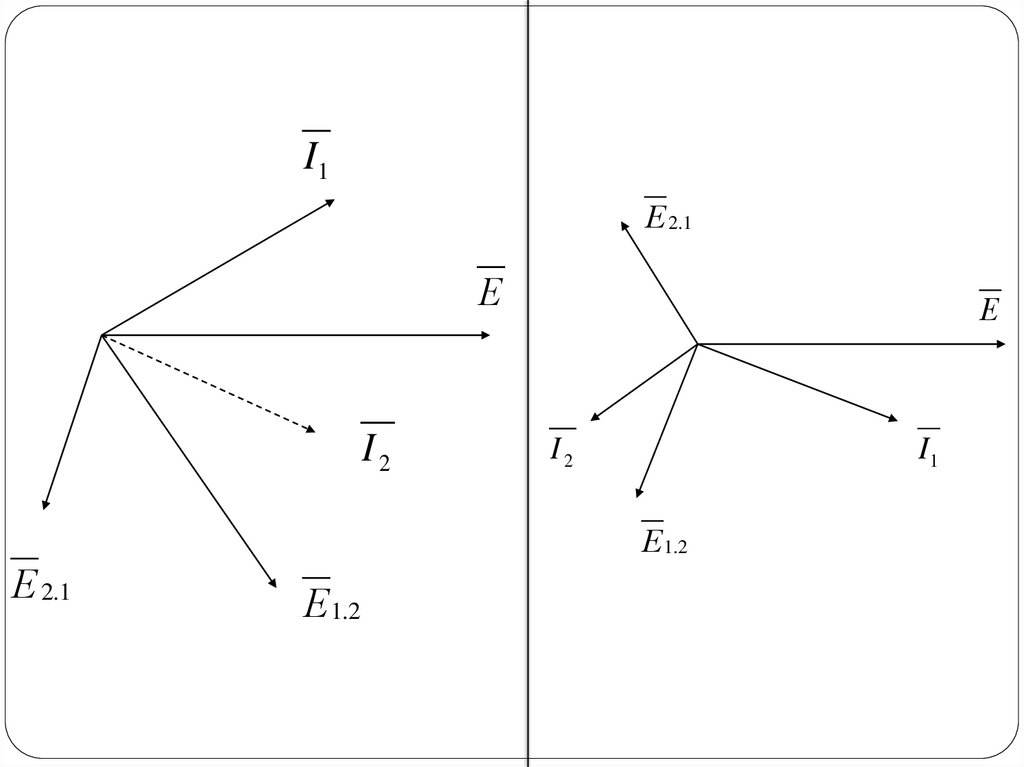
ЭКВИВАЛЕНТНЫЕ СХЕМЫ И ВЕКТОРНЫЕ ДИАГРАММЫ
ДЛЯ РАССТРОЕНОЙ СИСТЕМЫ ИЗ 2-Х КОНТУРОВ.
01 , 02
01 , 02
2
2
Z BX RBX
X BX
2
2
Z BX RBX
X BX
RBX r1 rBH
RBX r1 rBH
X BX X 1 X BH
X BX X 1 X BH
у Х BX - емкостной характер у Х BX - индуктивный
характер

31.

I1
Е 2.1
Е
I2
Е
I2
I1
Е1.2
Е 2.1
Е1.2

32.

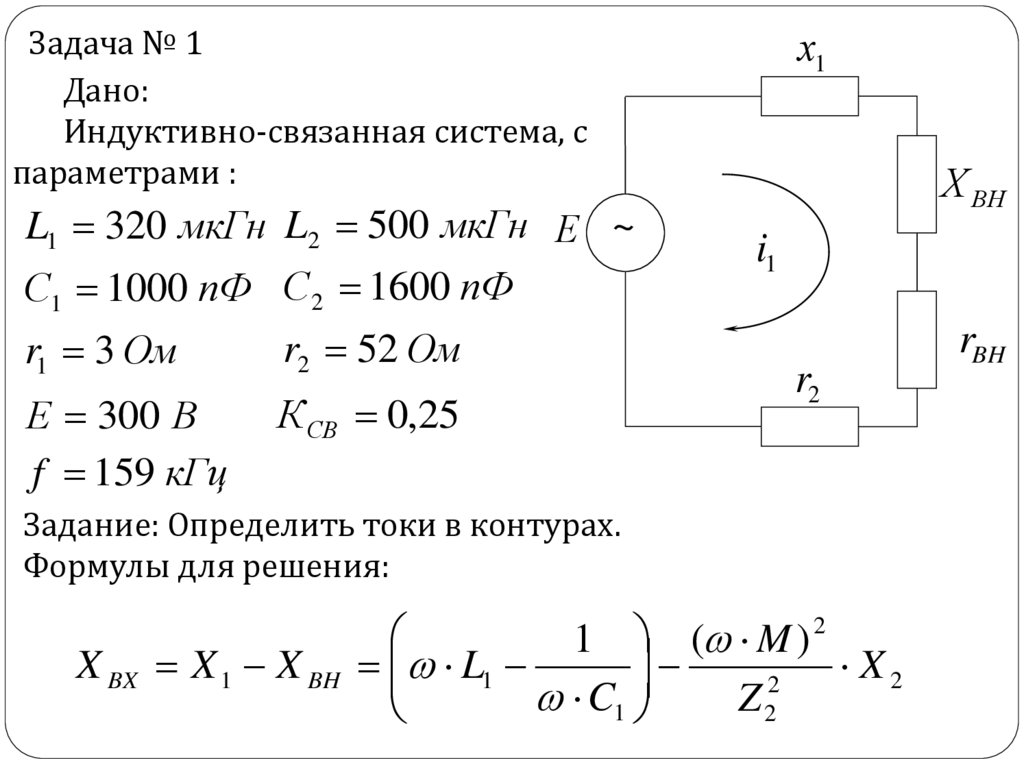
Задача № 1
Дано:
Индуктивно-связанная система, с
параметрами :
L1 320 мкГн L2 500 мкГн Е ~
С1 1000 пФ С 2 1600 пФ
r1 3 Ом
r2 52 Ом
Е 300 В
f 159 кГц
К СВ 0,25
х1
Х ВH
i1
r2
Задание: Определить токи в контурах.
Формулы для решения:
1 ( M ) 2
X BX X 1 X BH L1
X2
2
C1
Z2
rBH

33.

2
1
Z BX R X
Z 2 r L2
C2
E
E12 I 1 M
I1
2 f
I2
Z BX
Z2
Z2
2
1
(
M
)
X 2 L2
RBX r1 rBH r1
r2
2
C2
Z2
2
BX
2
BX
2
2
Z BX RBX
X BX
Ответы:
2
2
M K СВ L1 L2
I 1 0,5 A
I 2 0,36 A

34.

С помощью данных формул студентам предлагается
самостоятельно дома проделать все вычисления.
КПД СВЯЗАННОЙ СИСТЕМЫ
В связанной системе различают следующие мощности:
Р0 - мощность, потребляемая связанной системой от
генератора;
Р1 - мощность, расходуемая в первичном контуре;
Р2 - полезная мощность, которая расходуется во
вторичном контуре.
Тогда:
Р0 Р1 Р2 I 12 r1 I 22 r2
2
I
E
2
1 0 M
I 2 r2
r2
I 12 rBH
r2
r
1
12
2
2
2
Р0 Р1 Р2 I 12 r1 I 22 rBH

35.

P0 I12 r1 rBH
(23)
Коэффициентом полезного действия (КПД) системы
связанных контуров является число, показывающее какую
долю составляет мощность, передаваемая во вторичный
контур, от полной мощности, отдаваемой генератором.
Р2
Р2
rBH
100%
100%
100%
Р1
Р1 Р2
r1 rBH
Разделим на “rBH ” числитель и знаменатель, тогда
1
r1
1
rBH
100%
(24)

36.

Из выражения (24) очевидно, что
100% при rBH
при
50%
0
rBH r1
при rBH 0
Поскольку величина вносимого сопротивления определяется
величиной коэффициента связи между контурами, значит
КПД зависит от К СВ
СТЕПЕНИ СВЯЗИ МЕЖДУ КОНТУРАМИ
Для передачи наибольшей мощности во вторичный контур
из первичного, необходимо во вторичном контуре создать
наибольший по амплитуде ток.
I1 M
Ток I 2
(при резонансе) зависит от величины
r2
связимежду контурами, иначе, от коэффициента
взаимоиндукции М (общей взаимоиндуктивности).

37.

При изменении “М” меняется влияние вторичного контура
на первичный, а следовательно и ток I 1
Следовательно:
Ток зависит I 2 от двух переменных:I 1 и М.
Ток I 2 I 2 M MAX (максимально возможному) в том случае,
когда во вторичный контур передана максимальная
мощность, т.к.
Р2 I 22 r2 I12 rBH
(25)
Вторичный контур является нагрузкой для генератора.
Если применить к связанной системе условие передачи
максимальной мощности от генератора к нагрузке нагрузке
RH (RГЕН RH , где RГЕН - внутреннее сопротивление
генератора) и проанализировать значение мощности при
различных величинах коэффициента взаимоиндукции М, то
придём к следующим выводам:

38.

a) При M 0
rBH и P2 I12 rBH 0 , т.е. вся мощность Р0
расходуется в первичном контуре.
b) При M
rBH и P2 I12 rBH 0, за счёт того, что ток
E
I1
0
r1 rBH
c) Оптимальным вариантом величины связи между
контурами является соотношение P1 P2 , т.е. когда
распределение мощностей одинаково между контурами. А
это возможно при выполнении условия
I12 r1 I12 rBH , т.е когда
r1 rBH

39.

Величина связи, при которой во вторичный контур
передаётся максимальная мощность, называется
критической
M M KP
(26)
При критической связи r1 rBH . Т.е. если система настроена
в резонанс, то для получения во вторичном контуре
максимальной мощности необходимо выполнить условие
равенства активного сопротивления r1 первичного контура и
вносимого активного сопротивления rBH .
В связи с этим различают три степени связи
rBH r1
M M KP - слабая связь K K KP
Если
rBH r1 - M M KP - критическая
(оптимальная) связь K K KP
rBH r1
(27)
M M KP - сильная связь K K KP

40.

ЗАВИСИМОСТЬ ТОКОВ I1 , I 2 И КПД СИСТЕМЫ ОТ
КОЭФФИЦИЕНТА СВЯЗИ.
Токи в контурах зависят от коэффициента связи. При
изменении коэффициента связи меняется ЭДС, возбуждаемая
во вторичном контуре и вносимое сопротивление. Поэтому
изменяются токи I 1 и I 2 .
I1
E
2
M
0
r1
r
2
При увеличении “M” ток I 1 уменьшается, т.к.
увеличивается , rBH
0 M
2
r2
которое ослабляет ток первичного контура

41.

I1 0 M
I2
r2
При увеличении “M” ток I 2 вначале увеличивается, и при
связи
достигает своего максимального значения.
M
M
KP
Затем, с дальнейшим
увеличением “M” ток I 2 уменьшается,
за счёт уменьшения тока I 1 .
1
100%
r1
1
rBH
При увеличении “M” КПД увеличивается, т.к. увеличивается rBH
rBH 0
0
При
rBH
rBH r1
Отразим эти зависимости на графиках.
100%
50%

42.

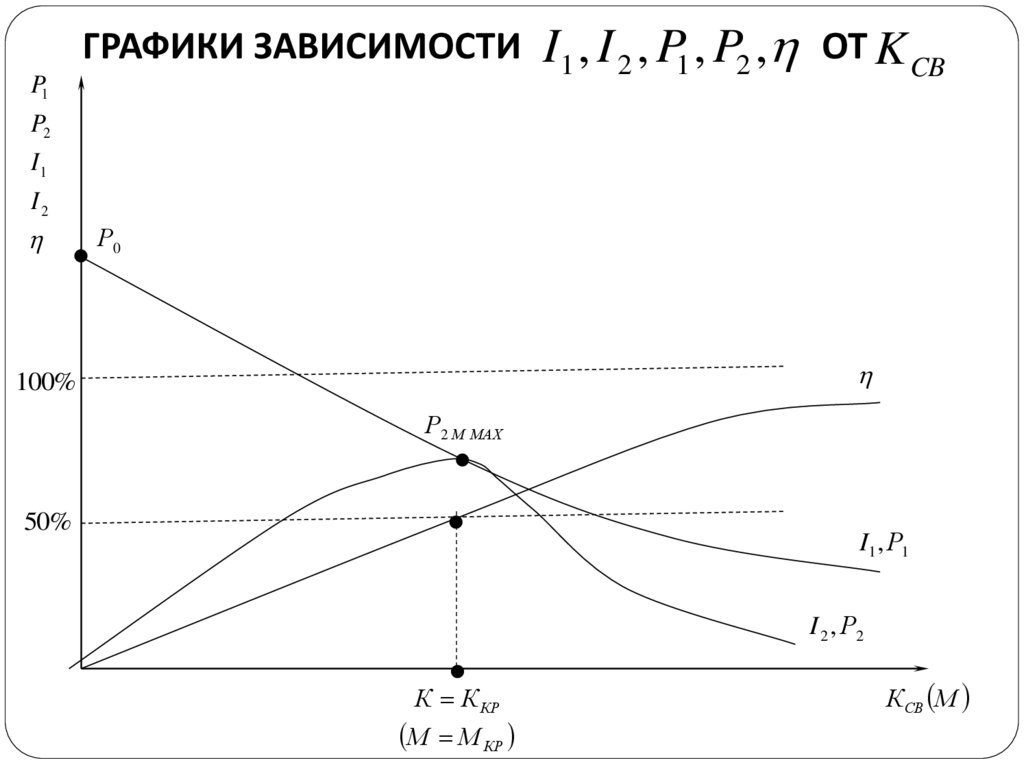
P1
ГРАФИКИ ЗАВИСИМОСТИ I1 , I 2 , P1 , P2 , ОТ K CB
P2
I1
I2
Р0
100%
Р2 М МАХ
50%
I1 , Р1
I 2 , Р2
К К КР
М М КР
К СВ М

43.

Из графиков очевидно, что повысить КПД можно
увеличением связи сверх её критического значения. При
K K KP КПД = 50%. Но повысив КПД сверх 50%,
одновременно уменьшим величину мощности, передаваемой
во вторичный контур. При K K KP полезная мощность Р2
уменьшается, т.к. уменьшается ток I 2 .
При - K K KP - P2 P2 M MAX
Определим коэффициенты взаимной индукции М, при
котором P2 P2 M MAX
Исходим из того, что r1 rBH
Отсюда r1
0 M KP
r2
2
,а M
KP
r1 r2
0
(28)
Определим значение коэффициента связи, соответствующее
критической связи

44.

r1 r2
M KP
K KP
L1 L2
0
r1 r2
r1 r2
2
0 L1 L2
0 L1 0 L2
L1 L2
1 1
т.к 0 L1 и 0 L2 , а
Q1 и
Q2
Q1 Q2
r1
r2
Если контура одинаковы, то Q1 Q2, а
1
K KP
Q
(29)
Как видно из (29) степень связи зависит не только от
коэффициента связи, но и от добротности контуров. Чем
ниже добротность, тем больше должен быть коэффициент
связи для передачи максимальной мощности во вторичный
контур.

45.

Определим значение сопротивления связи
X CB при K K KP
r1 rBH при K K KP
Значит
r1
X CB
2
r2
Откуда
X CB r1 r2
(30)

46.

Задача № 1
Дано: Индуктивно-связанная система с параметрами
M 0,1 мкГн
r2 4 Ом
rBH 3,2Ом
Определить 0
Задача № 2
В индуктивно-связанной системе
0 55 м
М 0,2 мкГн
r2 5 Ом
Определить rBH , X CB

47.

Задача № 3
Определить M KP индуктивно-связанной системы при
1 50 м
0 60 м
L2 16 мкГн
r1 5 Ом
r2 4 Ом

48.

НАСТРОЙКА СВЯЗАННЫХ КОНТУРОВ В РЕЗОНАНС
Цель настройки: передать во вторичный контур
максимальную мощность P2 P2 M MAX
Увеличение Р2 достигается за счёт увеличения I 2 .
Следовательно, в процессе настройки необходимо добиться,
чтобы показания прибора, регистрирующего величину тока
I 2, были максимальными, т.е. I 2 I 2 M MAX .
Существуют несколько способов настройки связанных
систем в резонанс:
1. 1-й частный резонанс
2. 2-й частный резонанс
3. Полный резонанс
4. Сложный резонанс

49.

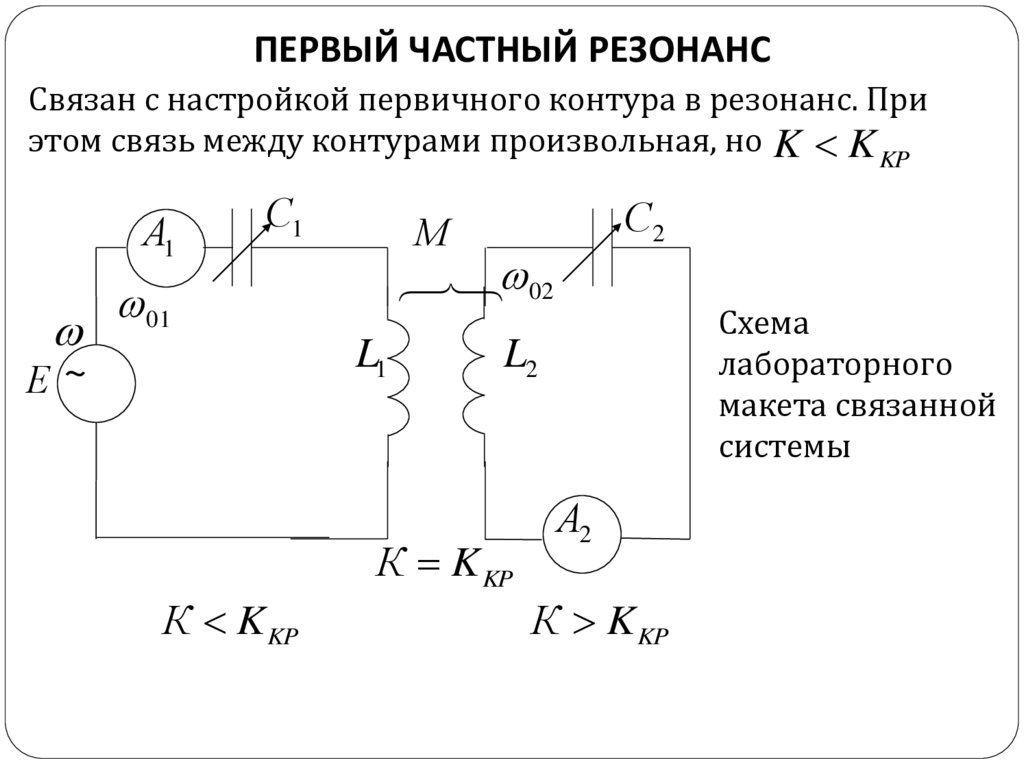
ПЕРВЫЙ ЧАСТНЫЙ РЕЗОНАНС
Связан с настройкой первичного контура в резонанс. При
этом связь между контурами произвольная, но K K KP
А1
С1
01
L1
Е~
Схема
лабораторного
макета связанной
системы
L2
К K KP
К K KP
С2
М
02
А2
К K KP

50.

Постоянные параметры при настройке:
E const
const
K CB const ( M const )
Изменяя ёмкость C добиваемся условия резонанса в
1
первичном контуре:
01
1
L1 C1
При этом амперметр A1 покажет наибольшую величину тока,
возможную при данном коэффициенте взаимоиндукции М.
но , I 1 MAX I 2 M MAX т.к. связь между контурами не
оптимальная ( K K ). При резонансе в первичном
KP
I
контуре ток 1 MAX наведёт во вторичном контуре E1.2 MAX ,
что, в свою очередь приведёт к получению I 2 MAX , т.е.
I 1 MAX E1.2 MAX I 2 MAX

51.

ГРАФИК ЗАВИСИМОСТИ ТОКОВ I 1 , I 2 ОТ ЧАСТОТЫ.
I1, 2
I1 MAX
I 2 MAX
I 2 M MAX
I2
I1
0
Вывод из графика:
При первом частном резонансе максимальному значению
тока I 1 MAX соответствует I 2 MAX . Но мощность, передаваемая
при этом во вторичный контур не максимально возможная
P2 MAX P2 M MAX , т.к. K K KP

52.

ВТОРОЙ ЧАСТНЫЙ РЕЗОНАНС
Связан с настройкой вторичного контура в резонанс. При
этом связь между контурами K K KP (M M KP )
Постоянные параметры при резонансе:
E const
const
K CB const ( M const )
Изменяя ёмкость C2 добиваемся условия резонанса во
вторичном контуре:
02
1
L2 C 2
при этом амперметр А2 покажет наибольшую величину тока,
возможную при данном коэффициенте взаимоиндукции М.
но ток I 2 I 2 M MAX , т.к. связь между контурами не
оптимальная.

53.

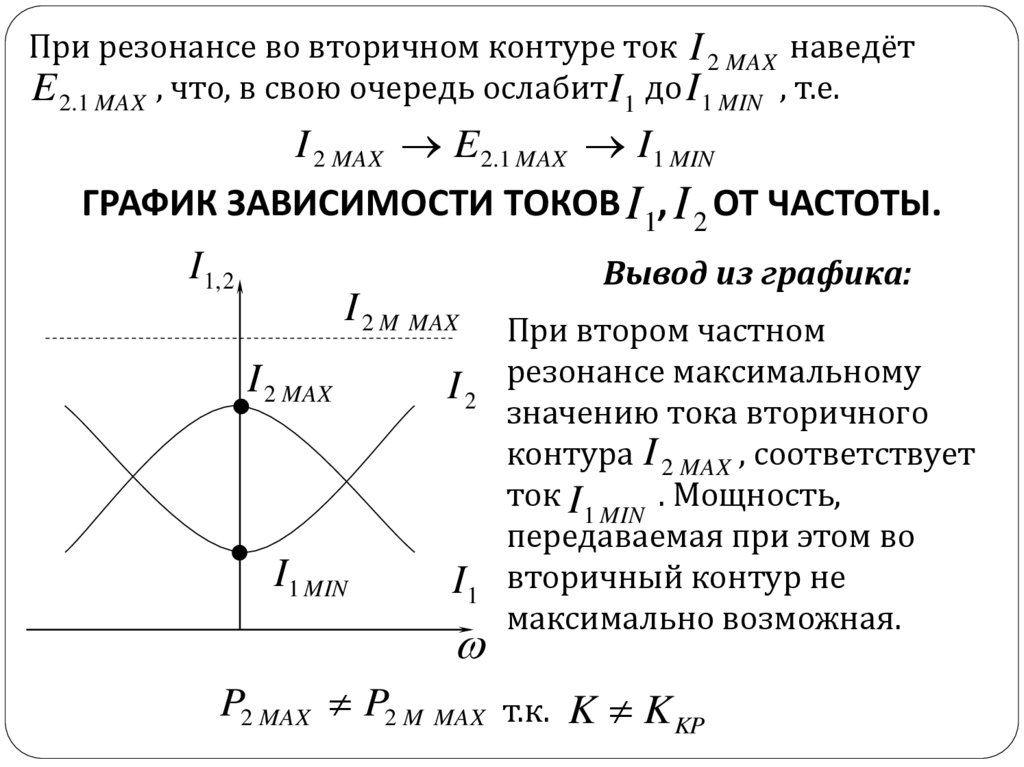
При резонансе во вторичном контуре ток I 2 MAX наведёт
E 2.1 MAX , что, в свою очередь ослабитI 1 до I 1 MIN , т.е.
I 2 MAX E 2.1 MAX I 1 MIN
ГРАФИК ЗАВИСИМОСТИ ТОКОВ I 1, I 2 ОТ ЧАСТОТЫ.
I1, 2
Вывод из графика:
I 2 M MAX
I 2 MAX
I2
I1 MIN
I1
При втором частном
резонансе максимальному
значению тока вторичного
контура I 2 MAX , соответствует
ток I
. Мощность,
1 MIN
передаваемая при этом во
вторичный контур не
максимально возможная.
P2 MAX P2 M MAX т.к. K K KP

54.

ПОЛНЫЙ РЕЗОНАНС
Настройка связанной системы в полный резонанс
осуществляется в 3 этапа:
I этап.
Настройка первичного контура в резонанс, следствием чего
является X 1 0, I 1 I 1 MAX
II этап
Настройка вторичного контура в резонанс, следствием чего
является X 2 0 , I 2 I 2 MAX
III этап
Подбор оптимальной связи между контурами K K KP. .
При этом добиваемся передачи во вторичный контур
мощности P2 P2 M MAX .
X1 0, X 2 0
(31)
X BX 0 т.к. X 1 0, X 2 0
(31) – признак полного резонанса.

55.

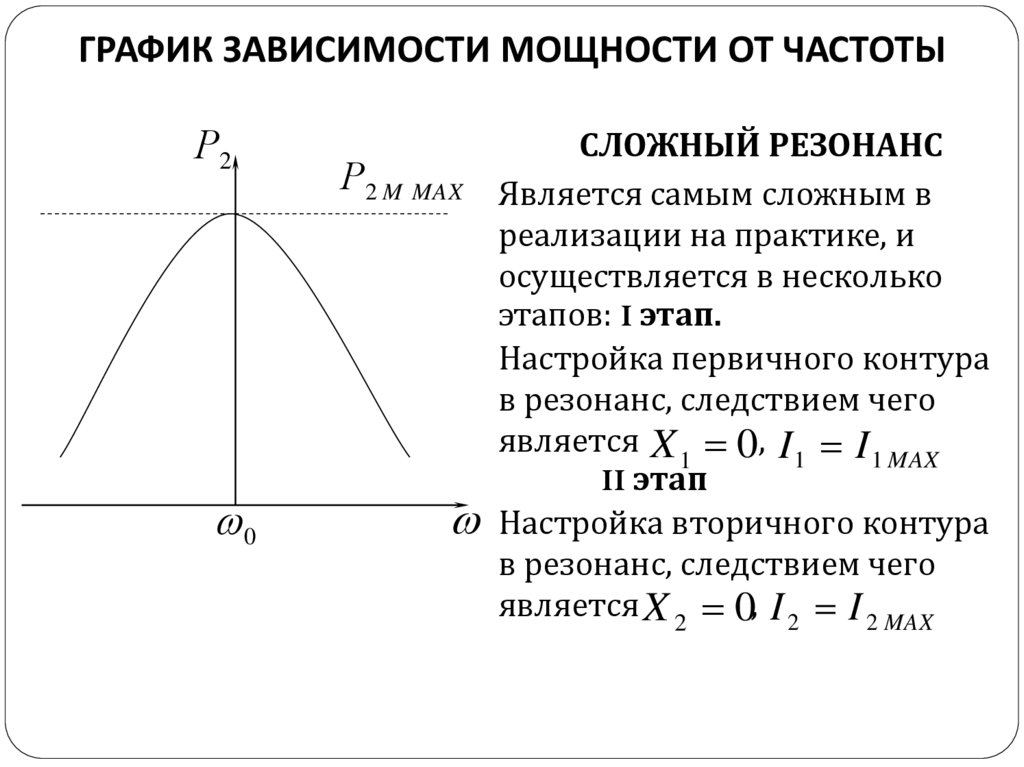
ГРАФИК ЗАВИСИМОСТИ МОЩНОСТИ ОТ ЧАСТОТЫ
Р2
0
СЛОЖНЫЙ РЕЗОНАНС
Р2 M MAX Является самым сложным в
реализации на практике, и
осуществляется в несколько
этапов: I этап.
Настройка первичного контура
в резонанс, следствием чего
является X 1 0, I 1 I 1 MAX
II этап
Настройка вторичного контура
в резонанс, следствием чего
является X 2 0, I 2 I 2 MAX

56.

III этап
Подбор оптимальной связи между контурами K K KP . При
этом добиваемся передачи во вторичный контур мощности
P2 P2 M MAX .
IV этап
Увеличением “M” (усилением связи K K KP ) добиваемся на
частоте 01 02 значения мощности
P
P2
2 M MAX
2
V этап
Зафиксировав связь K K KP соответствующую IV этапу,
расстроить систему до получения P2 P2 M MAX , следствием
чего будет X BX 0 , т.к. X 1 X BH
(32) – признак сложного резонанса.
(32)

57.

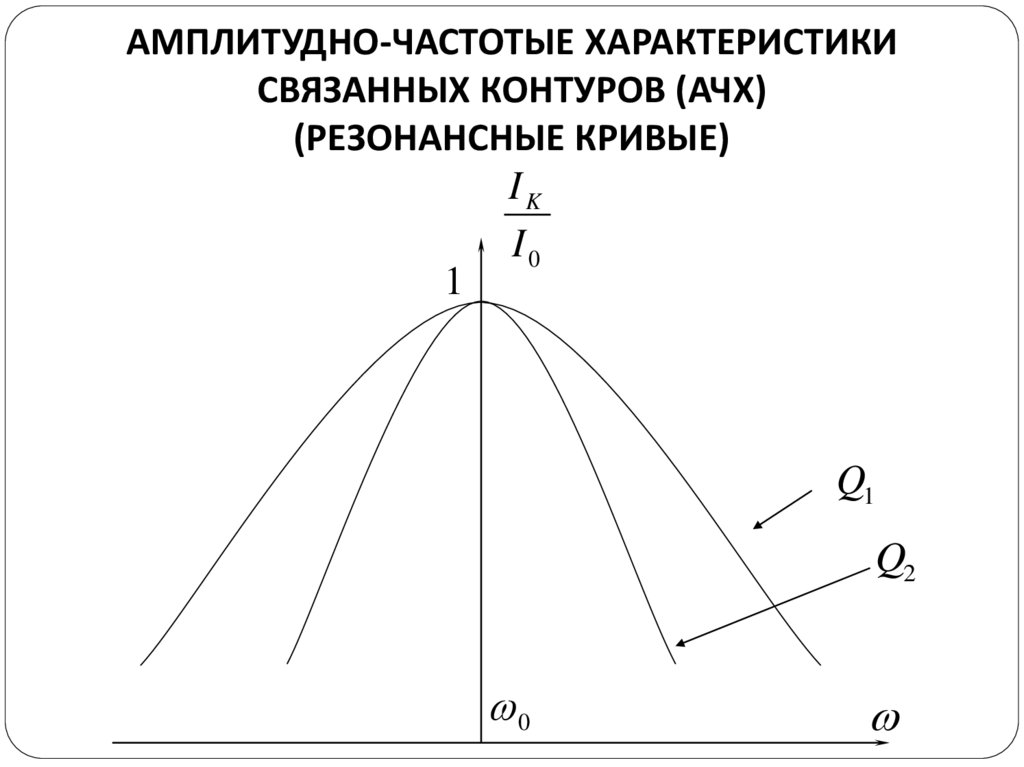
АМПЛИТУДНО-ЧАСТОТЫЕ ХАРАКТЕРИСТИКИ
СВЯЗАННЫХ КОНТУРОВ (АЧХ)
(РЕЗОНАНСНЫЕ КРИВЫЕ)
IK
I0
1
Q1
Q2
0

58.

В одиночных контурах вид резонансной кривой зависит
только от параметра: Q1 Q 2
f0
2 f
Q
В системе связанных контуров резонансная кривая зависит
от двух параметров:
o- добротность Q
o- степени связи между контурами K CB
Зафиксировав параметр Q , рассмотрим зависимость
резонансной кривой от связи между контурами на примере
двухконтурной индуктивно-связанной системы.
Рассмотрим 3 случая:
1. K K KP ;
rBH r1
(M M KP )
2. K K KP ;
rBH r1
(M M KP )

59.

3. K K KP ;
rBH r1
(M M KP )
1. Связь между контурами критическая
M M KP
( K K KP )
Полный резонанс.
а) На резонансной 01, 2 частоте наблюдается
соотношение:
r1 rBH
0 M KP 2
r2
(32)
т.к. r1 rBH, то выполняется условие передачи
максимальной мощности во вторичный контур, а ток
I 2 I 2 M MAX

60.

б) На частотах, отличных от резонансной ( 01, 2 )
наблюдается соотношение:
r1 rBH
M KP 2
r X
2
2
2
2
r2
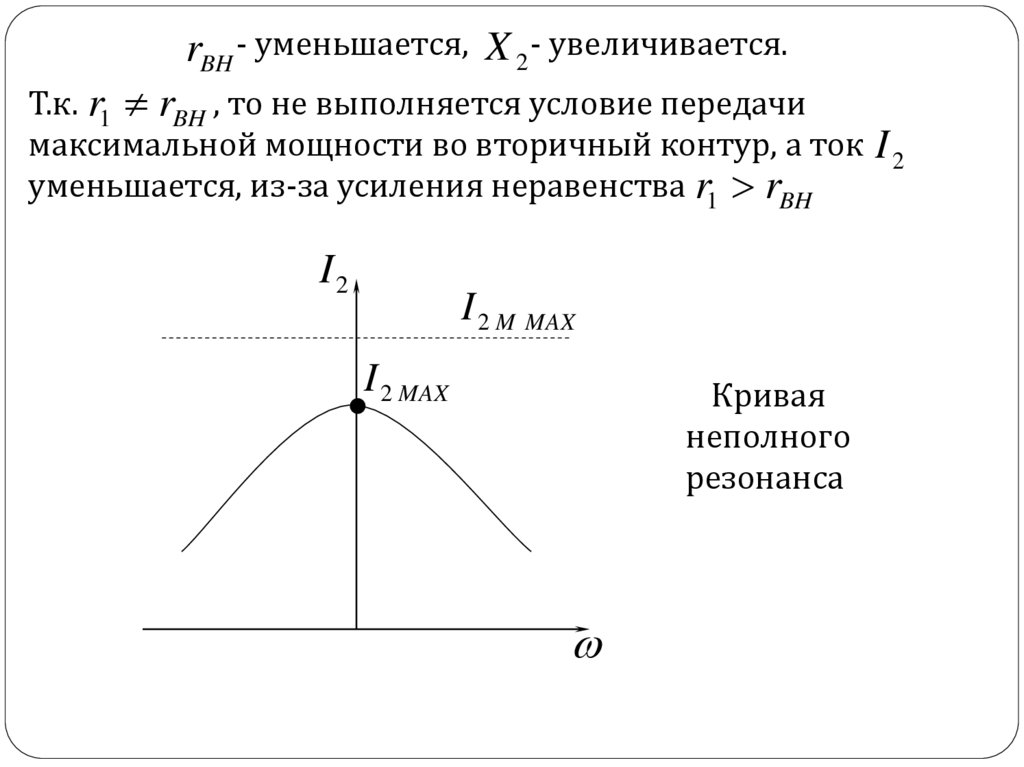
rBH - уменьшается, X 2 - увеличивается.
т.к. r1 rBH , то нарушается условие передачи максимальной
мощности во вторичный контур, а ток I 2 - уменьшается.
I2
I 2 M MAX
Кривая полного
резонанса
0

61.

2. Связь между контурами слабая
M M KP
( K KKP )
а) На резонансной частоте ( ) наблюдается
01.2
соотношение:
r1 rBH
0 M
2
r2
Т.к. r1 rBH то не выполняется условие передачи
максимальной мощности во вторичный контур, а ток
I 2 I 2 M MAX
б) На частотах отличных от резонансной, наблюдается
соотношение:
( M ) 2
r1 rBH 2
r2
2
r2 X 2
(34)

62.

rBH - уменьшается, X 2 - увеличивается.
Т.к. r1 rBH , то не выполняется условие передачи
максимальной мощности во вторичный контур, а ток I 2
уменьшается, из-за усиления неравенства r1 rBH
I2
I 2 M MAX
I 2 MAX
Кривая
неполного
резонанса

63.

3. Связь между контурами сильная (rBH r1 ) (M M KP )
Сложный резонанс.
а) На резонансной частоте ( 01, 2 ) наблюдается
соотношение:
r1 rBH
0 M 2
r2
(35)
Т.к. r1 rBH , то не выполняется условие передачи
максимальной мощности во вторичный контур, а ток
I 2 I 2 M MAX
I , II
б) На частотах
(боковые частоты), отличных от
резонансных наблюдается соотношение:
( M )
r1 rBH
r2
2
2
r2 X 2
I , II
2
(36)

64.

Т.е на боковых частотах и имеем условие передачи
максимальной мощности во вторичный контур, т.к. r1 rBH ,
а следовательно I 2 I 2 M MAX
I
II
в) Удаляясь влево и вправо от боковых частот, вновь
нарушается условие r1 rBH , т.к
( M ) 2
r1 rBH 2
r2
2
r2 X 2
r1 rBH -уменьшается, X 2 - увеличивается, а ток I 2
следовательно уменьшается.
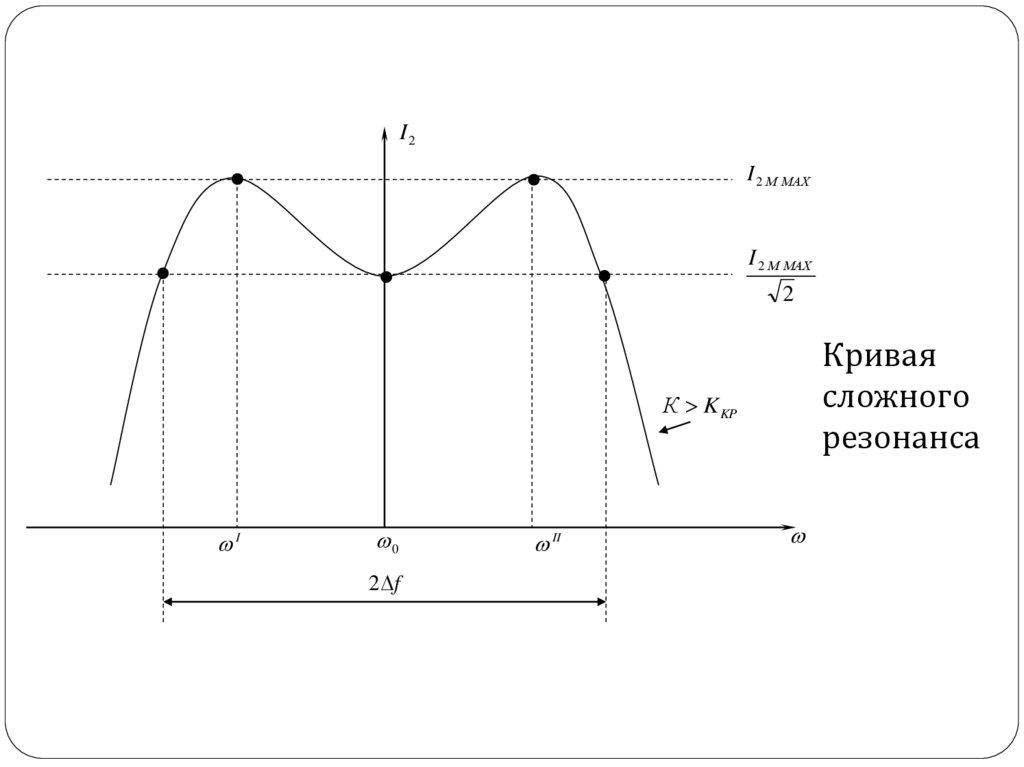
При сложном резонансе максимальным ток I 2 будет на
I
II
боковых частотах и .

65.

I2
I 2 М МАХ
I 2 М МАХ
2
Кривая
сложного
резонанса
К K KP
I
0
2 f
II

66.

Сводная таблица 3-ч случаев резонанса
Неполный
Полный резонанс Сложный резонанс
резонанс K K KP
K K
K K
KP
условие резонанса
признак резонанса
на
на
I , II
на 012
II
01 02
01 02
I , II
X1 0 X 2 0
X BX 0
X1 0 X 2 0
X BX 0
X 1 X BH
X BX 0
I 2 M MAX
I2
2
I 2 MAX I 2 M MAX I 2 MAX I 2 M MAX
01.2
I
KP
I 2 I 2 MAX
I 2 I 2 MAX
I 2 MAX I 2 M MAX
I 2 I 2 M MAX
I 2 I 2 M MAX
I 2 I 2 MAX

67.

I2
I 2 M MAX
I2
I 2 M MAX
I2
I 2 M MAX
I 2 M MAX
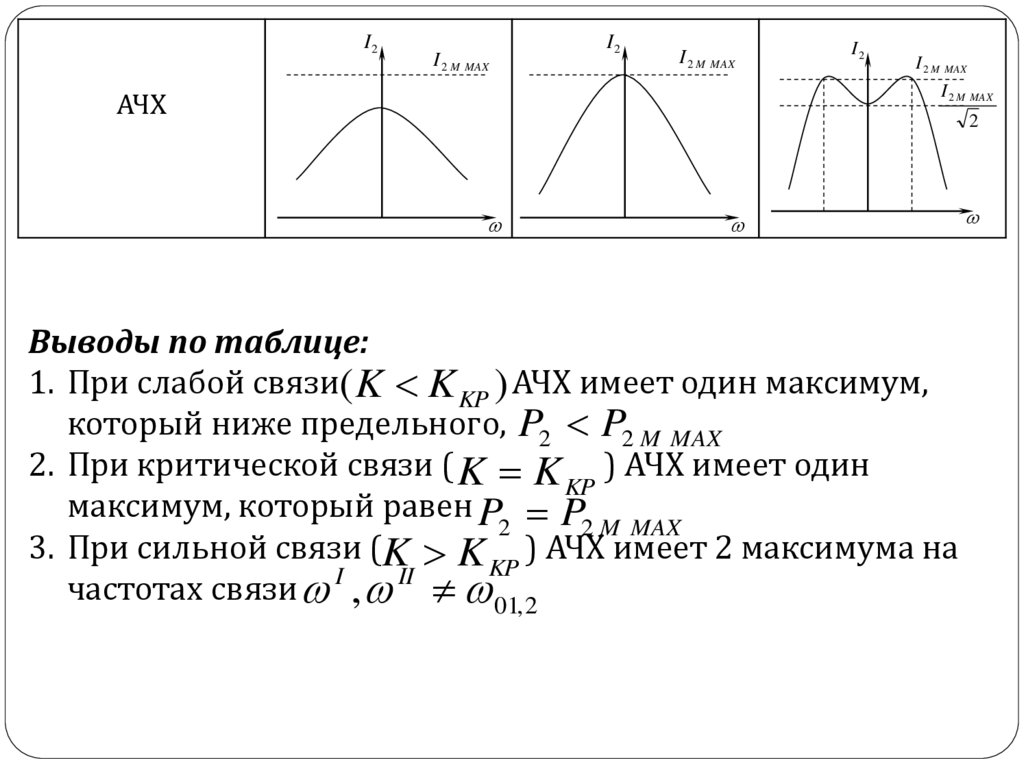
АЧХ
2
Выводы по таблице:
1. При слабой связи( K K KP ) АЧХ имеет один максимум,
который ниже предельного, P2 P2 M MAX
2. При критической связи ( K K ) АЧХ имеет один
KP
максимум, который равен P P
2
2 M MAX
3. При сильной связи (K K ) АЧХ имеет 2 максимума на
KP
I
II
частотах связи , 01, 2

68.

I ( II )
M Z2
r1
r1
2
2
r2 X 2
r2
r2
r1
r2
r1 r2 0 M КР
r2
т.е. полный резонанс – частный случай сложного.
4. При полном резонансе
M M KP
X CB X CB KP r1 r2 0
(37)
5. При сложном резонансе
M M KP
I
0
1 K
X CB Z 2
I
r1
r2
0
1 K
(38)
(39)

69.

ПОЛОСА ПРОПУСКАНИЯ СВЯЗАННОЙСИСТЕМЫ
Полосой пропускания системы связанных контуров
называют полосу (спектр) частот, в пределах которой ток во
вторичном контуре падает не более чем 2 в раз
относительно резонансного значения.
Резонансные кривые АЧХ показали, что полоса пропускания
при различных степенях связи между контурами различны.
Это позволяет регулировать полосу пропускания системы.
При сильной связи ( К К КР ) полоса пропускания
наиболее широкая. Но беспредельно усиливать связь нельзя,
т.к. величина тока I 2 в провале кривой сложного резонанса
должна быть. I 2
I 2 M MAX
2
Это получается при K 2,41 K KP .

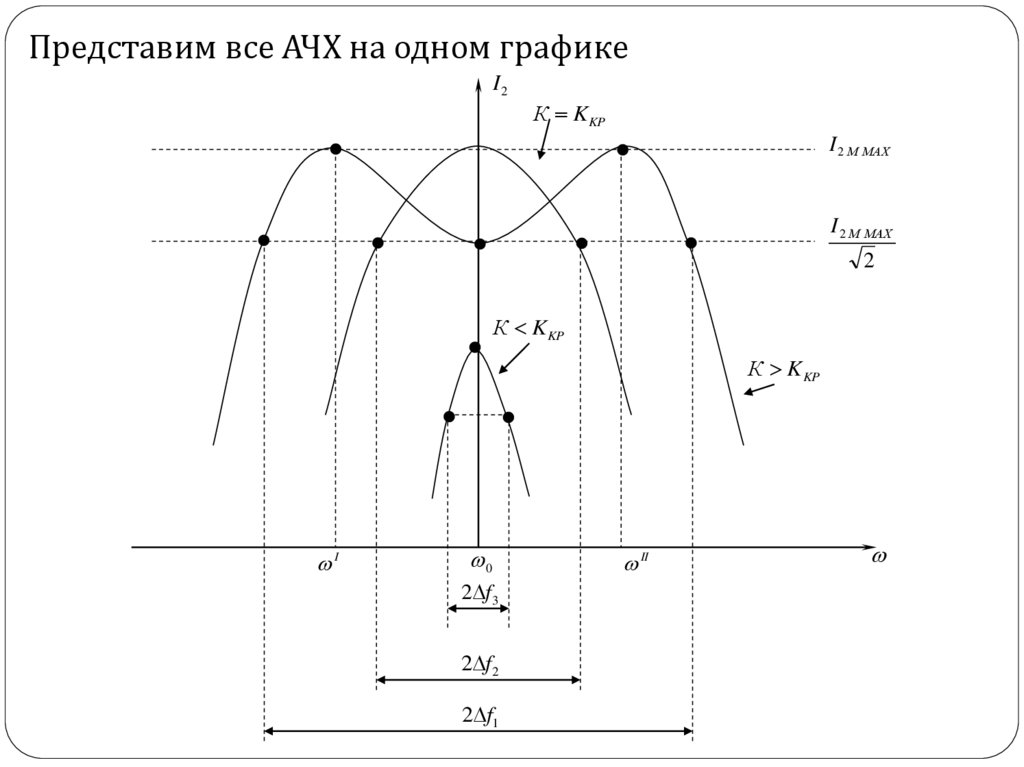
70.

Представим все АЧХ на одном графике
I2
К K KP
I 2 М МАХ
I 2 М МАХ
2
К K KP
К K KP
I
0
2 f 3
2 f 2
2 f1
II

71.

f0
1) 2 f 1 0,65
при K 0,1 K KP
Q
(40)
f0
2) 2 f 2 1,41
Q
(41)
3)
при K K KP
f 0 при K 2,41 K
(42)
2 f 3 3,1
KP
Q
ДОСТОИНСТВА СИСТЕМЫ СВЯЗАННЫХ КОНТУРОВ
1. Возможность получения широкой полосы пропускания
при достаточно высокой добротности.
2. возможность регулирования ширины полосы пропускания
за счёт изменения связи между контурами.
3. Наличие частот связи при сильной степени связи
позволяет получить максимальную величину тока во
вторичном контуре.

72.

НЕДОСТАТКИ СИСТЕМЫ СВЯЗАННЫХ КОНТУРОВ.
1. Сложность настройки в резонанс.
2. Низкий КПД системы при Р2 Р2 М МАХ (КПД = 50%).
3. Неэкономичность.
ПРИМЕНЕНИЕ СВЯЗАННЫХ КОНТУРОВ.
Используется в качестве нагрузки в супергетеродинном
приёмнике.
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО РАЗДЕЛУ № 5
1. Понятие о связанных контурах. Коэффициенты связи.
Виды связанных контуров.
2. Вносимые сопротивления, их физический смысл,
зависимость вносимых сопротивлений от коэффициента
связи. Изменение вносимых сопротивлений при
изменении частоты. Эквивалентная схема связанных
контуров.

73.

3. Необходимость увеличения тока в цепи вторичного
контура. Настройка системы связанных контуров.
Частные резонансы. Значение тока в первичном и
вторичном контурах и их изменение при отклонении
частоты генератора при частных резонансах.
4. Получение в цепи вторичного контура максимально
возможного тока. Полный резонанс. Значение токов в
цепях контуров. При полном резонансе. Сопротивление,
вносимое при полном резонансе.
5. Оптимальная связь. Коэффициент оптимальной связи, его
зависимость от параметров контура. КПД системы
связанных контуров, его зависимость от связи между
контурами.
6. АЧХ первичного контура системы связанных контуров
при различных значениях коэффициента связи. Причины
появления частот связи при коэффициенте связи больше
критического.

74.

7. АЧХ вторичного контура системы связанных контуров.
Сложный резонанс. Уравнение резонансной кривой
вторичного контура.
8. Полоса пропускания системы связанных контуров.
Зависимость полосы пропускания от коэффициента связи.
Полоса пропускания при критической связи,
максимальная полоса пропускания, избирательность,
область использования связанных контуров.
КОНТРОЛЬНЫЕ ЗАДАЧИ ПО РАЗДЕЛУ №5.
Задача № 1
В индуктивно-связанной системе M 0,1 мкГн , r2 4 Ом
rBH 2,5 Ом , 0 ?
Задача № 2
В индуктивно-связанной системе f 0 6 МГц ,
M 0,2 мкГн , r2 10 Ом , rBH ?

75.

Задача № 3
В индуктивно-связанной системе с параметрами K CB 0,3 ,
L1 30 мкГн , L2 20 мкГн , определить М.
Задача № 4
Определить K CB у системы с автотрансформаторной связью,
если LСВ 10 мкГн , L 20 мкГн , L 30 мкГн
1
2
Задача № 5
Определить K CB , если Х CB 32 Ом , L1 10 мкГн ,
L2 20 мкГн
Задача № 6
Определить М КР , если известно, что 1 50 м , 0 60 м ,
L2 20 мкГн , r1 10 Ом , r2 6 Ом

76.

Задача № 7
Определить K CB в системе с внешне-емкостной связью,
если известно, что С1 200 пФ , С1 ССВ 100 пФ
Задача № 8
В индуктивно-связанной системе с параметрами Е 300 В,
f 160 кГц , L1 320 мкГн , С1 1000 пФ , r1 3 Ом ,
rBH 5 Ом , Х BH 70 Ом . Определить I 1 , Z BX , RBX , X BX .
Задача № 9
Определить вносимое сопротивление для индуктивносвязанной системы, если известно, что L 320 мкГн ,
1
L2 500 мкГн , K CB 0,25 , f 160 кГц , r 50 Ом ,
Х L 300 Ом
2