Основные понятия. Математические доказательства. Способы математических доказательств

1.

Основные понятия
Математические доказательства.
Способы математических
доказательств.

2.

Основные понятия
Теорема
это высказывание, истинность
которого
устанавливается
посредством
рассуждения (доказательства).
-
С логической точки зрения теорема – это высказывание вида
А В,
где А и В высказывательные формы с одной или несколькими
переменными.
2

3.

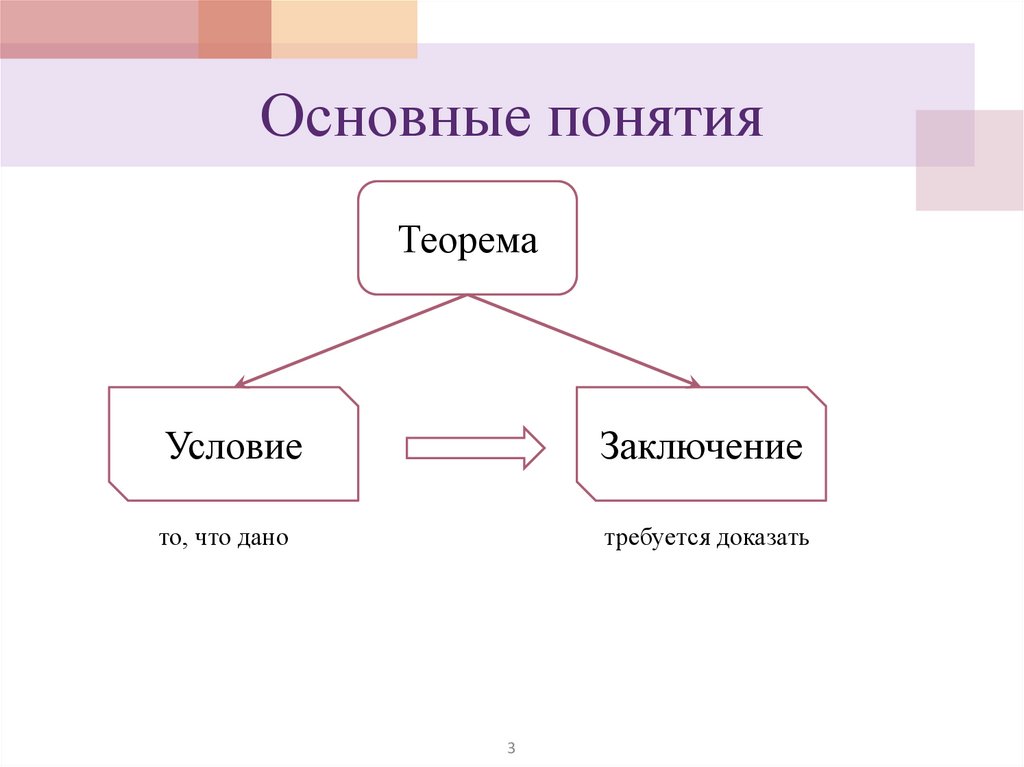
Основные понятия
Теорема
Условие
Заключение
то, что дано
требуется доказать
3

4.

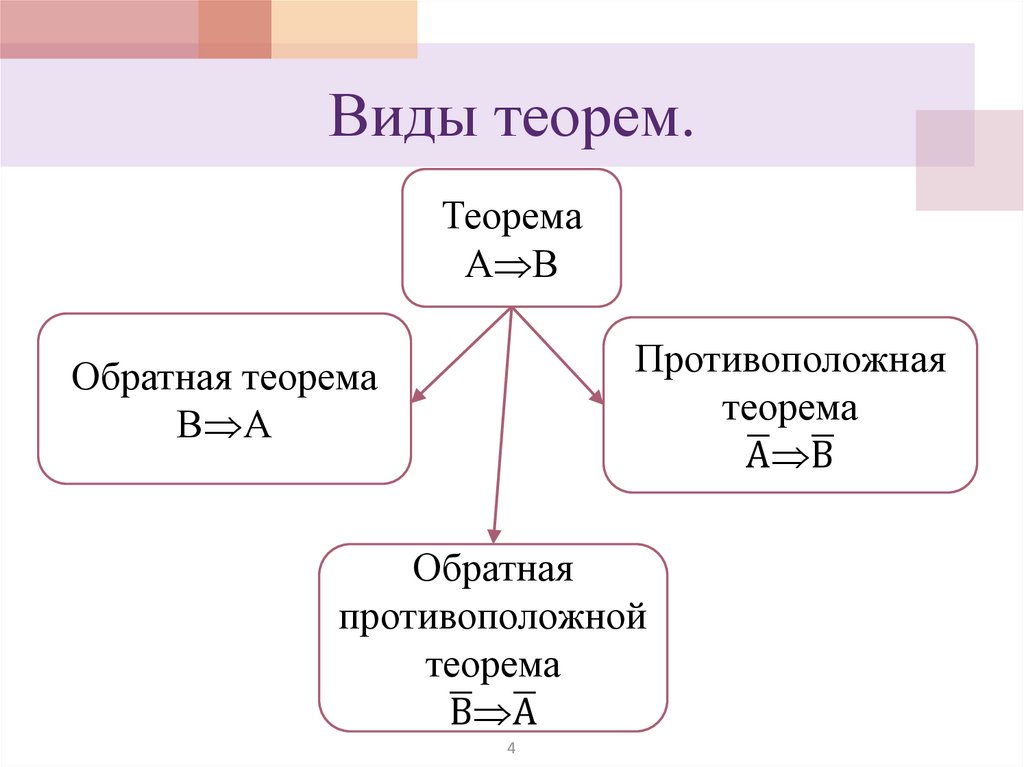
Виды теорем.
Теорема
А В
Противоположная
теорема
ഥ В
ഥ
А
Обратная теорема
В А
Обратная
противоположной
теорема
ഥ
ഥ А
В
4

5.

Виды теорем.
5

6.

Закон контрапозиции.
Позволяет:
1. Вместо данной теоремы можно доказывать теорему, обратную
противоположной данной.
2. Предложение, обратное данному, и предложение,
противоположное данному, одновременно истины либо
одновременно ложны (поэтому достаточно доказать какоенибудь одно).
6

7.

Основные формы мышления:
- Понятие
- Высказывание
- Умозаключение
Умозаключение (рассуждение) – это способ получения нового
знания на основе некоторых имеющихся.
7

8.

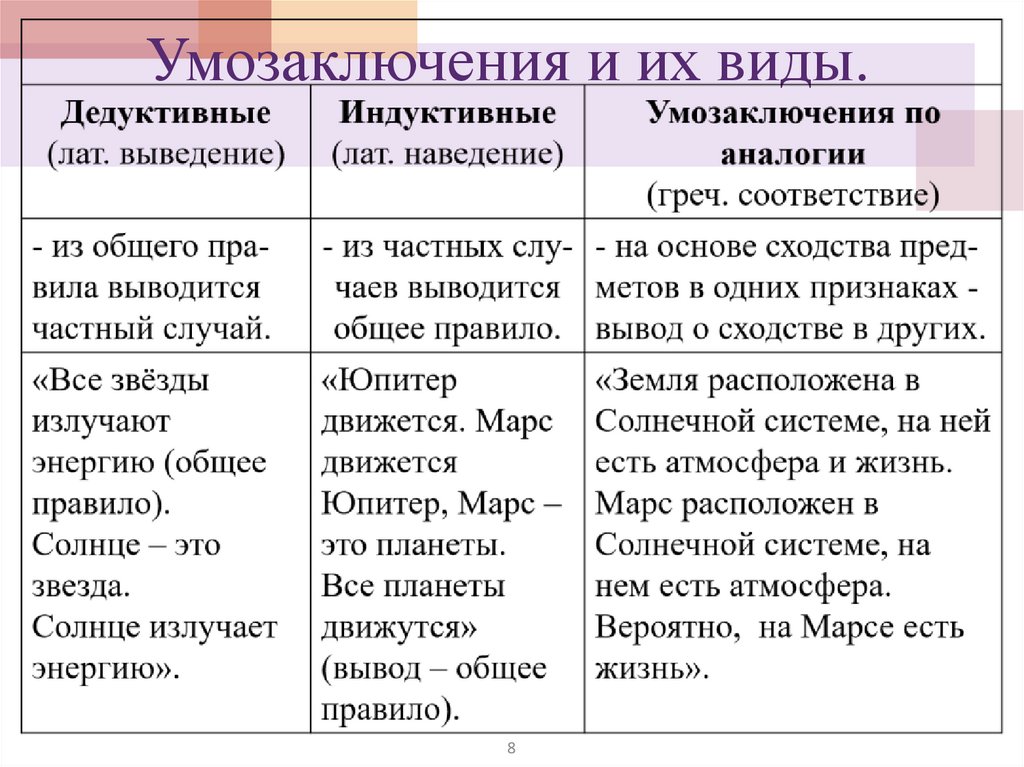
Умозаключения и их виды.
8

9.

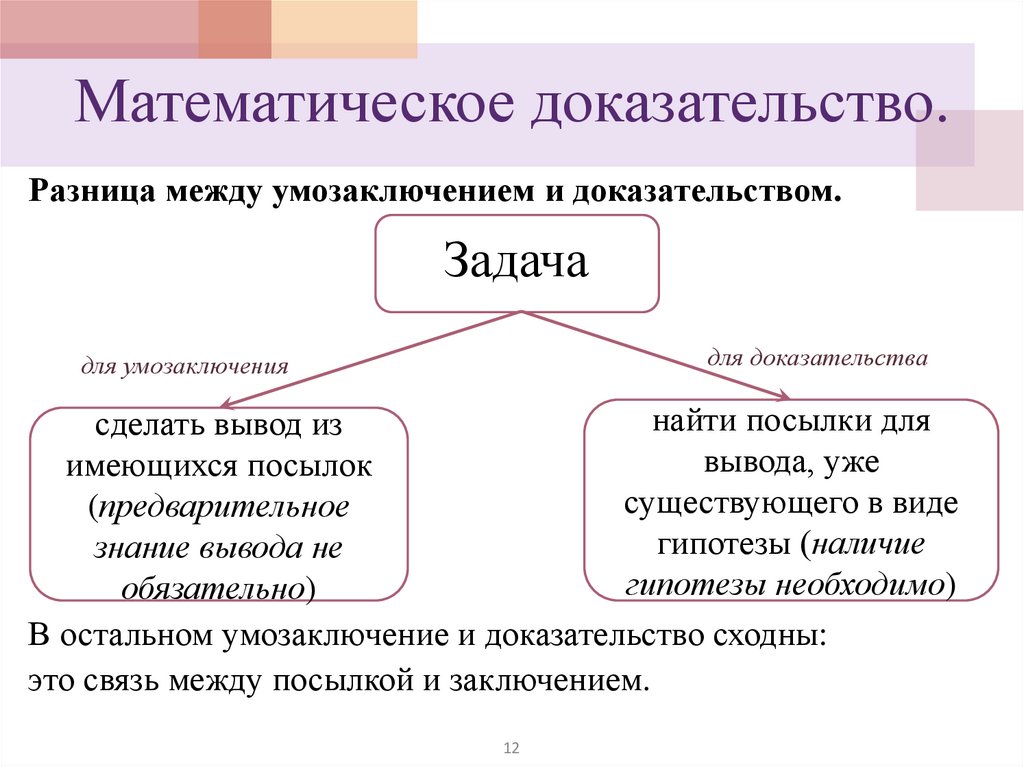
Математическое доказательство.
Разница между умозаключением и доказательством.
Задача
для доказательства
для умозаключения
найти посылки для
сделать вывод из
вывода, уже
имеющихся посылок
существующего в виде
(предварительное
гипотезы (наличие
знание вывода не
гипотезы необходимо)
обязательно)
В остальном умозаключение и доказательство сходны:
это связь между посылкой и заключением.
12

10.

Математическое доказательство.
Доказательство
- это совокупность логических приемов
обоснования истинности утверждения.
В доказательстве выделяют следующие структурные элементы:
1. доказываемое утверждение;
2. систему истинных утверждений, с помощью которых
обосновывается истинность доказываемого;
3. логическую связь между пп.1 и 2.
Основной способ математического доказательства – дедуктивный метод.
По форме доказательство – это дедуктивное умозаключение или
цепочка дедуктивных умозаключений, ведущих от истинных
посылок к доказываемому утверждению.
13

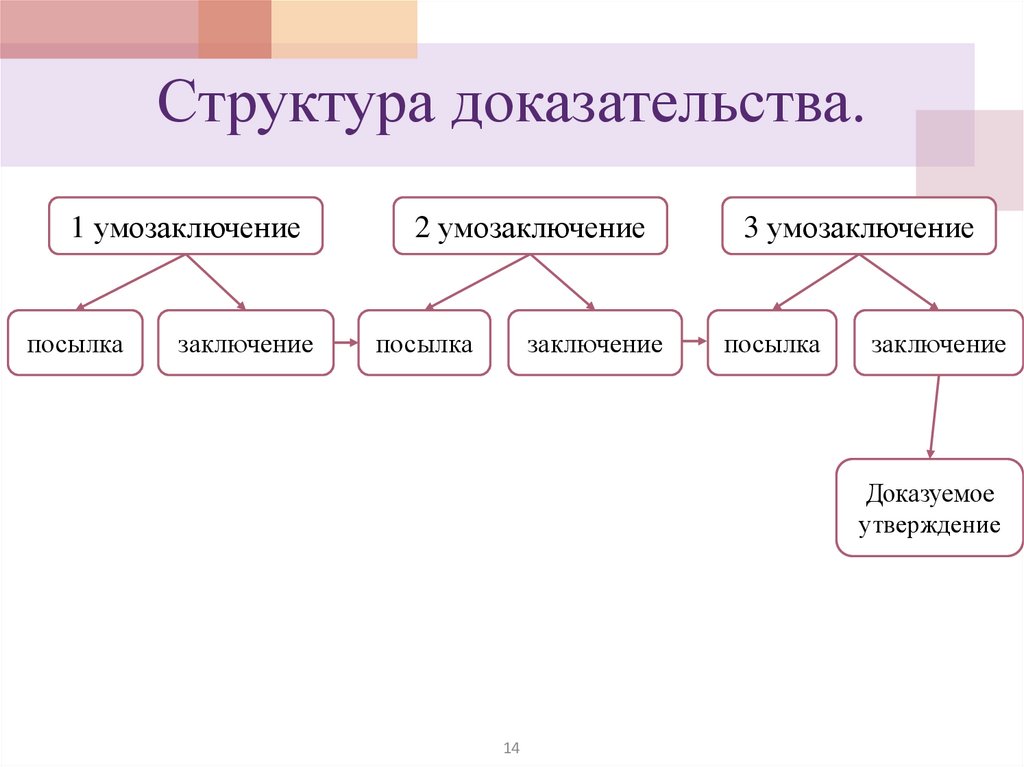
11.

Структура доказательства.
1 умозаключение
посылка
заключение
2 умозаключение
посылка
заключение
3 умозаключение
посылка
заключение
Доказуемое
утверждение
14

12.

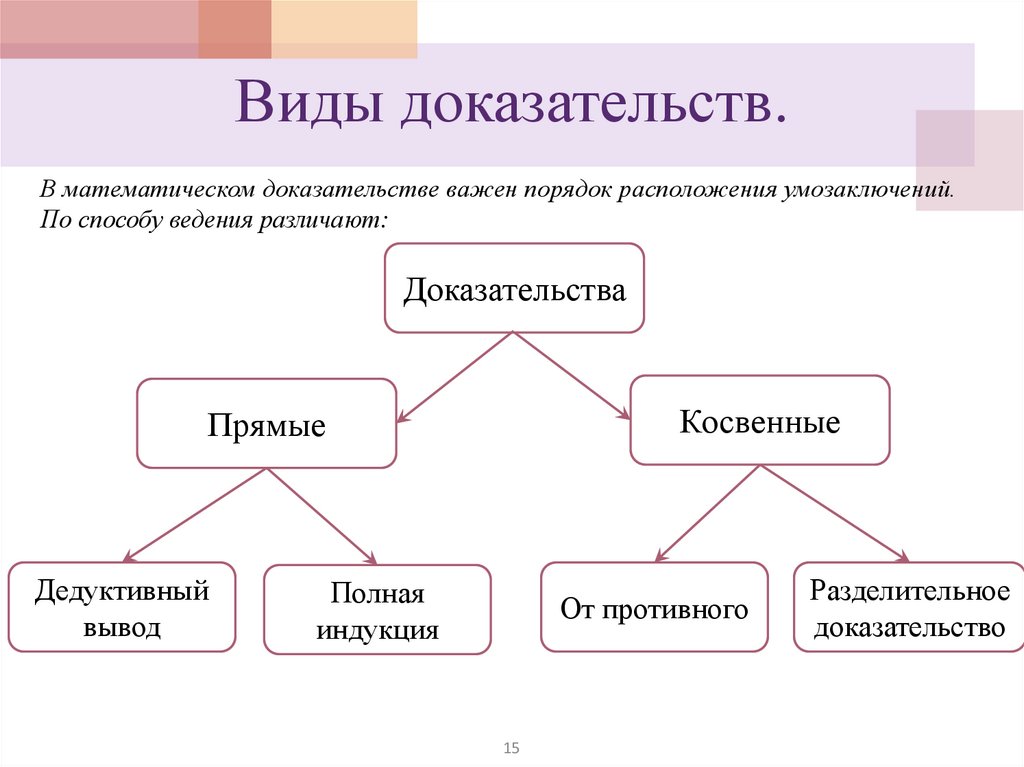
Виды доказательств.
В математическом доказательстве важен порядок расположения умозаключений.
По способу ведения различают:
Доказательства
Косвенные
Прямые
Дедуктивный
вывод
Полная
индукция
От противного
15
Разделительное
доказательство

13.

Математическое доказательство.
Прямое доказательство утверждения А В - это
построение цепочки дедуктивных умозаключений,
выполняемых последовательно от А к В с соблюдением
правил логики и с помощью системы утверждений,
истинность которых доказана.
16

14.

Математическое доказательство.
Пример, требуется доказать, что
если в четырехугольнике три угла прямые, то
он прямоугольник.
Рассмотрим произвольный четырехугольник, в котором три угла
прямые:
так как в любом выпуклом четырехугольнике сумма углов 360⁰,
то и в данном она составляет 360⁰;
сумма трех прямых углов равна 270⁰ (90⁰*3 = 270⁰), и, значит,
четвертый имеет величину 90⁰ (360⁰ -270⁰ =90⁰);
Если все углы четырехугольника прямые, то он – прямоугольник.
Следовательно,
данный
четырехугольник
будет
17
прямоугольником. Что и требовалось
доказать.

15.

Математическое доказательство.
В доказательстве можно выделить следующие умозаключения :
В любом выпуклом четырехугольнике сумма углов равна 360⁰;
данная фигура – выпуклый четырехугольник, следовательно,
сумма углов в нем 360⁰.
2. Если известна сумма всех углов четырехугольника и сумма трех из
них, то вычитанием можно найти величину четвертого; сумма всех
углов данного четырехугольника равна 360⁰, сумма трех 270⁰ (90⁰•3
= 270⁰), то величина четвертого 360⁰ - 270⁰ = 90⁰.
3. Если в четырехугольнике все углы прямые, то этот
четырехугольник – прямоугольник; в данном четырехугольнике все
углы прямые, следовательно, он прямоугольник.
1.
Все приведенные умозаключения выполнены по правилу заключения
и, следовательно, являются дедуктивными.
18

16.

Математическое доказательство.
Полная индукция – способ доказательства, при котором
истинность утверждения следует из его истинности во всех
частных случаях.
Пример,
требуется установить, что каждое натуральное чётное число n в пределах
2< n < 22
представимо в виде суммы двух простых чисел.
Для этого возьмём все такие числа и выпишем соответствующие разложения:
4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5; 14=7+7; 16=11+5; 18=13+5;
20=13+7.
Эти девять равенств показывают, что каждое из интересующих нас чисел
действительно представляется в виде суммы двух простых слагаемых.
Что и требовалось доказать.
19

17.

Математическое доказательство.
Метод от противного – метод доказательства теоремы (утверждения),
состоящий в том, что доказывают не саму теорему, а ей равносильную
обратную противоположной теорему.
Этапы метода от противного:
1. Предполагаем противоположное тому, что нужно доказать.
2. В ходе рассуждения приходим к противоречию с ранее изученной
аксиомой, теоремой или условием задачи.
3. Отрицаем предположение как неверное.
4. По закону исключенного третьего делаем вывод.
Пример,
В классе 20учеников. Докажите, что среди них найдутся двое, празднующих день
рождения в одном месяце.
Решение:
Предположим, что это не так, и среди 20 учеников нет двоих, празднующих день
рождения в одном месяце. То есть в каждом месяце день рождения не больше, чем у
одного ученика. Всего месяцев 12. Если сложить не более чем 12 единиц, получим
число не больше, чем 12. А 20 больше, чем 12 –мы пришли к противоречию. Значит,
наше предположение о том, что в каждом месяце день рождения не больше, чем у
одного ученика, неверно. Поэтому должен быть хотя бы один месяц, в котором день
рождения празднуют больше одного ученика, т.е. хотя бы двое.
Что и требовалось доказать.
20

18.

Математическое доказательство.
Разделительное доказательство характеризуется тем, что из
нескольких
возможных
тезисов
методом
исключения
доказывается один.
Например, известно, что данное преступление совершили или А,
или В, или С (и никто другой). Затем последовательно
приводятся доказательства, что этого сделать не могли ни А, ни
В. Таким образом доказывается, что преступление совершил С.
Здесь важно лишь, чтобы были исчерпаны все возможные
варианты, т. е. чтобы дизъюнкция была полной, «закрытой».
Объективные различия между прямыми и косвенными
доказательствами относительны: прямое доказательство может
быть превращено в косвенное, а косвенное – в прямое.
21

19.

Спасибо за внимание.
22