Различные способы доказательства теоремы Пифагора

1. Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №1 с углубленным изучением отдельных

предметов города Искитима
Новосибирской области»
И С С Л Е Д О ВАТ Е Л Ь С К И Й П Р О Е К Т
П О М АТ Е М АТ И К Е :
« РА З Л И Ч Н Ы Е С П О С О Б Ы Д О К А З А Т Е Л Ь С Т В А
Т Е О Р Е М Ы П И Ф А Г О РА »
ВЫПОЛНИЛ:
УЧЕНИЦА 10 КЛАССА
МБОУ-СОШ №1 Г. ИСКИТИМА
ЕЗОВА КСЕНИЯ ВЯЧЕСЛАВОВНА
РУКОВОДИТЕЛЬ ПРОЕКТА:
ГРИКО ЛЮДМИЛА ВАСИЛЬЕВНА
УЧИТЕЛЬ МАТЕМАТИКИ
МБОУ-СОШ №1 Г. ИСКИТИМА
2025г.
г.Искитим

2. Содержание:

СОДЕРЖАНИЕ:
Введение
1. История появления теоремы
2. 9 способов доказательства теоремы Пифагора:
1 способ доказательства теоремы Пифагора
2 способ доказательства теоремы Пифагора
3 способ доказательства теоремы Пифагора
4 способ доказательства теоремы Пифагора
5 способ доказательства теоремы Пифагора
6 способ доказательства теоремы Пифагора
7 способ доказательства теоремы Пифагора
8 способ доказательства теоремы Пифагора
9 способ доказательства теоремы Пифагора
2.1 Исследование знаний о теореме.
2.2 Применение теоремы в различных областях жизни
Заключение
Источники

3. Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами

1. Введение
ТЕОРЕМА ПИФАГОРА — ОДНА ИЗ ОСНОВОПОЛАГАЮЩИХ ТЕОРЕМ ЕВКЛИДОВОЙ
ГЕОМЕТРИИ, УСТАНАВЛИВАЮЩАЯ СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ
ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА: СУММА КВАДРАТОВ ДЛИН КАТЕТОВ РАВНА
КВАДРАТУ ДЛИНЫ ГИПОТЕНУЗЫ.
В СВОЕЙ РАБОТЕ Я РАССМОТРЕЛА 9 СПОСОБОВ ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ
ПИФАГОРА, О КОТОРЫХ ВЫ УЗНАЕТЕ ДАЛЬШЕ.
ЦЕЛЬ ИССЛЕДОВАНИЯ: ВЫЯСНИТЬ РАЗЛИЧНЫЕ СПОСОБЫ ДОКАЗАТЕЛЬСТВА
ТЕОРЕМЫ ПИФАГОРА
ЗАДАЧИ: ИССЛЕДОВАТЬ РАЗЛИЧНЫЕ СПОСОБЫ ДОКАЗАТЕЛЬСТВА ДАННОЙ
ТЕОРЕМЫ.
1. ПРОВЕСТИ ОПРОС СРЕДИ УЧАЩИХСЯ В ВИДЕ АНКЕТИРОВАНИЯ ДЛЯ ВЫЯВЛЕНИЯ
ЗНАНИЙ О ТЕОРЕМЕ ПИФАГОРА.
2. УСТАНОВИТЬ КАКОЕ ЗНАЧЕНИЕ ИМЕЕТ ОТКРЫТИЕ ТЕОРЕМЫ В РАЗВИТИИ
МАТЕМАТИКИ.
3. ВЫЯСНИТЬ ГДЕ МОЖЕТ ПРИМЕНЯТЬСЯ ТЕОРЕМА В ПОВСЕДНЕВНОЙ ЖИЗНИ.
4. ОБРАБОТАТЬ ПОЛУЧЕННЫЕ ДАННЫЕ И СДЕЛАТЬ ВЫВОД.
ГИПОТЕЗА: ЕСЛИ ТЕОРЕМА ПИФАГОРА ПОПУЛЯРНА И СЕГОДНЯ, ТО В НЕЙ ЗАЛОЖЕНЫ
ТАКИЕ ОСНОВЫ, КОТОРЫЕ ПОЗВОЛЯЮТ ИСПОЛЬЗОВАТЬ ЕЕ В ШИРОКОМ ДИАПАЗОНЕ.

4. 1. История появления теоремы

1. ИСТОРИЯ ПОЯВЛЕНИЯ ТЕОРЕМЫ
Пифагор — древнегреческий философ и математик, основатель
пифагорейской школы. Он известен своими вкладами в математику,
астрономию и философию. Пифагор считается автором знаменитой теоремы,
которая описывает соотношение между сторонами прямоугольного
треугольника. Его учение оказало значительное влияние на развитие науки и
философии в Древней Греции.
Раньше мне было неизвестно, что теорема Пифагора была открыта не самим
Пифагором. Свойства прямоугольного треугольника изучались задолго до него, и
есть две точки зрения на вопрос авторства доказательства: по одной версии его
нашёл Пифагор, по другой — нет.
Доказательство Пифагора, если оно существовало, не сохранилось. Есть
предположение, что доказательство из «Начал» Евклида может принадлежать
Пифагору.
Задачи о прямоугольном треугольнике встречаются в источниках Древнего Египта,
Вавилона, Индии и Китая.
В времена Пифагора теорема звучала так: квадрат, построенный на гипотенузе
прямоугольного треугольника, равновелик сумме квадратов, построенных на
катетах. В современных учебниках формулировка короче: в прямоугольном
треугольнике квадрат гипотенузы равен сумме квадратов катетов.

5. 2. 9 способов доказательства теоремы Пифагора:

2. 9 СПОСОБОВ
ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ
ПИФАГОРА:
• 1 способ доказательства теоремы Пифагора:
Используя геометрические свойства площадей многоугольников, мы можем вывести
соотношение между гипотенузой и катетами прямоугольного треугольника.
Доказательство:
Рассмотрим прямоугольный треугольник с катетами а, в и гипотенузой с
Докажем, что с²=а²+в².
Достроим треугольник до квадрата со стороной а + в так, как показано на 2 рисунке.
Площадь S этого квадрата равна (а + в)² . Но, если посмотреть с другой стороны, этот
квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из
которых равна ½ав , и квадрата со стороной с , поэтому S= 4 * ½ав + с² =2ав + с².
Таким образом, (а + в)² = 2ав + с², откуда с²=а²+в².
Теорема доказана.

6. 2 способ доказательства теоремы Пифагора:

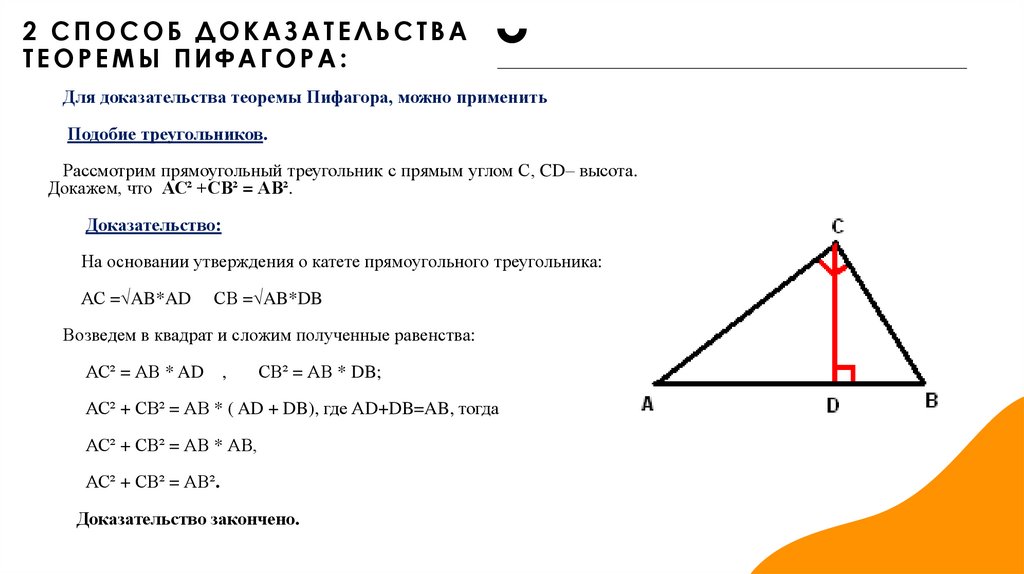
2 СПОСОБ ДОКАЗАТЕЛЬСТВА
ТЕОРЕМЫ ПИФАГОРА:
Для доказательства теоремы Пифагора, можно применить
Подобие треугольников.
Рассмотрим прямоугольный треугольник с прямым углом С, CD– высота.
Докажем, что АС² +СВ² = АВ².
Доказательство:
На основании утверждения о катете прямоугольного треугольника:
АС =√AB*AD
СВ =√AB*DB
Возведем в квадрат и сложим полученные равенства:
АС² = АВ * AD ,
СВ² = АВ * DB;
АС² + СВ² = АВ * ( AD + DB), где АD+DB=AB, тогда
АС² + СВ² = АВ * АВ,
АС² + СВ² = АВ².
Доказательство закончено.

7. 3 способ доказательства теоремы Пифагора:

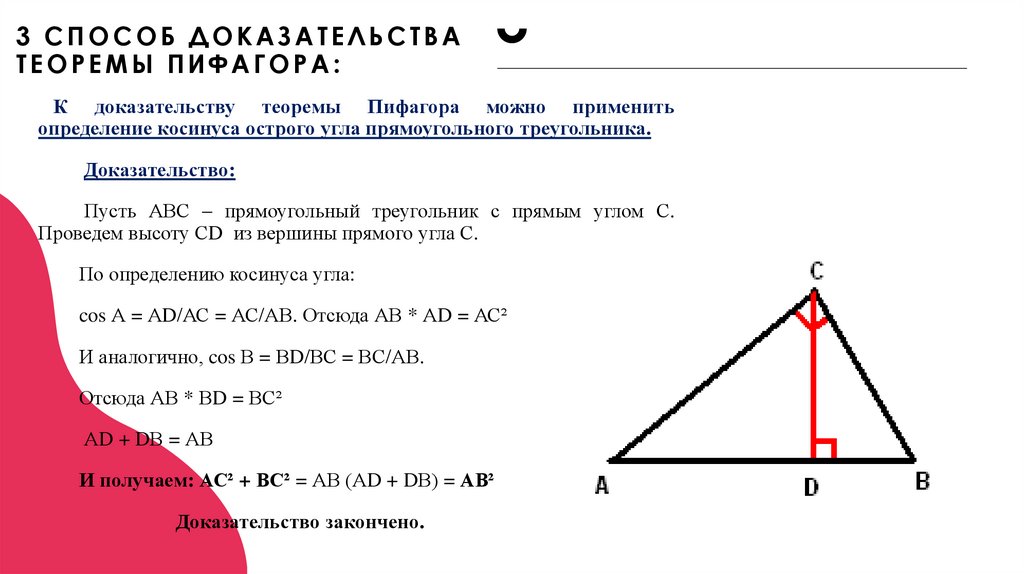
3 СПОСОБ ДОКАЗАТЕЛЬСТВА
ТЕОРЕМЫ ПИФАГОРА:
К доказательству теоремы Пифагора можно применить
определение косинуса острого угла прямоугольного треугольника.
Доказательство:
Пусть АВС – прямоугольный треугольник с прямым углом С.
Проведем высоту СD из вершины прямого угла С.
По определению косинуса угла:
cos А = АD/АС = АС/АВ. Отсюда АВ * АD = АС²
И аналогично, cos В = ВD/ВС = ВС/АВ.
Отсюда АВ * ВD = ВС²
АD + DВ = АВ
И получаем: АС² + ВС² = АВ (АD + DВ) = АВ²
Доказательство закончено.

8. 4 способ доказательства теоремы Пифагора:

4 СПОСОБ ДОКАЗАТЕЛЬСТВА
ТЕОРЕМЫ ПИФАГОРА:
Теорему Пифагора можно доказать ещё одним способом,
используя тему «Соотношения между сторонами и углами
прямоугольного треугольника».
Рассмотрим прямоугольный треугольник с катетами а, в и
гипотенузой с.
Докажем, что с²=а²+в².
Доказательство:
sinВ= в/с ; cosВ= a/с, то получим:sin²В= в²/с²; cos²В= а²/с².
Сложив их, получим: sin²В + cos²В= в²/с²+ а²/с², где sin²В +
cos²В=1, 1= (в²+ а²) / с²,
следовательно, с²= а² + в².
Доказательство закончено.

9. 5 способ доказательства теоремы Пифагора:

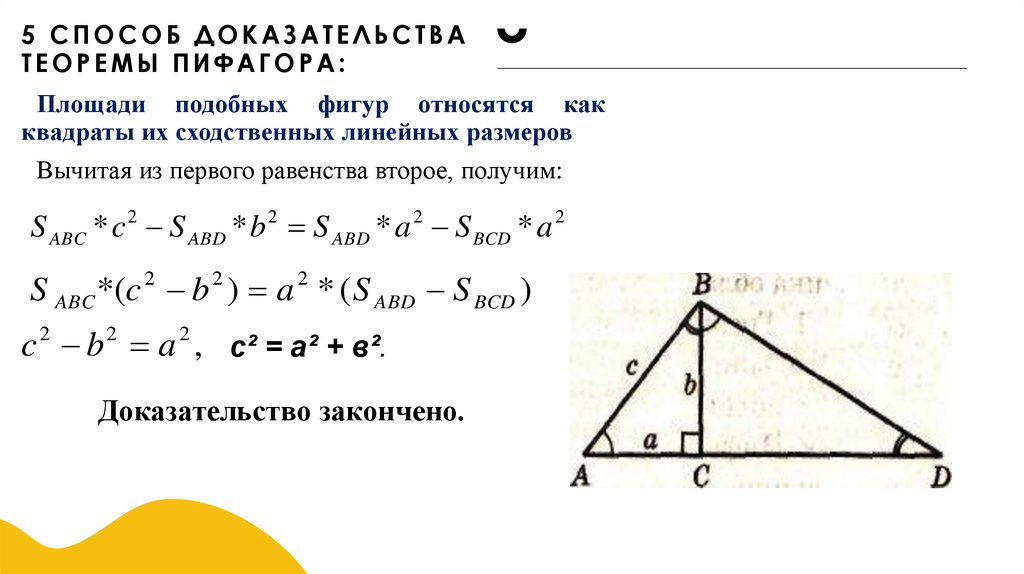
5 СПОСОБ ДОКАЗАТЕЛЬСТВА
ТЕОРЕМЫ ПИФАГОРА:
Площади подобных фигур относятся как
квадраты их сходственных линейных размеров
Вычитая из первого равенства второе, получим:
S ABC * c 2 S ABD * b 2 S ABD * a 2 S BCD * a 2
S ABC *(c b ) a * ( S ABD S BCD )
2
2
2
c b a , с² = а² + в².
2
2
2
Доказательство закончено.

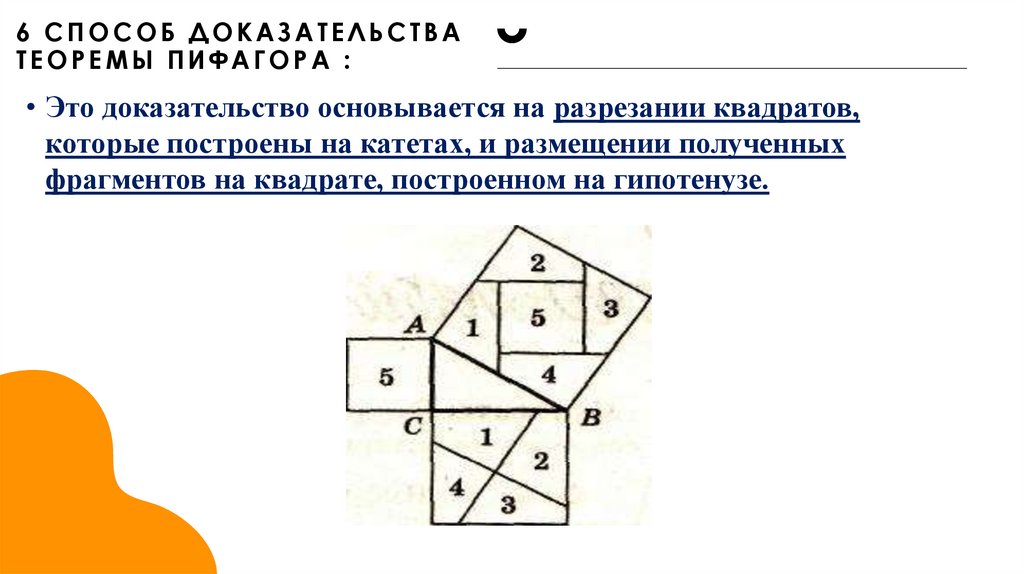
10. 6 способ доказательства теоремы Пифагора :

6 СПОСОБ ДОКАЗАТЕЛЬСТВА
ТЕОРЕМЫ ПИФАГОРА :
• Это доказательство основывается на разрезании квадратов,
которые построены на катетах, и размещении полученных
фрагментов на квадрате, построенном на гипотенузе.

11. 7 способ доказательства теоремы Пифагора:

7 СПОСОБ ДОКАЗАТЕЛЬСТВА
ТЕОРЕМЫ ПИФАГОРА:
Площадь данного прямоугольного треугольника, с одной
стороны, равна ½ab , с другой, ½pr , где р - полупериметр
треугольника, r - радиус вписанной в него окружности.
Доказательство:
1) r= ½ (a+b+c)
2) ½ab = ½pr = ½(a+b+c)* ½(a+b-c), откуда следует, что с² = а²
+ в²
Доказательство закончено.

12. 8 способ доказательства теоремы Пифагора :

8 СПОСОБ ДОКАЗАТЕЛЬСТВА
ТЕОРЕМЫ ПИФАГОРА :
На рисунке, три прямоугольных треугольника образуют
трапецию.
Следовательно,
площадь
этой
фигуры
можно
вычислить,
используя
формулу
для
площади
прямоугольной трапеции, или же найдя сумму площадей
трех треугольников.
В первом случае эта площадь равна ½(a+b)(a+b), во втором
-½ab + ½ab + ½ с2.
Приравнивая эти уравнения, мы приходим к теореме
Пифагора.
½(a+b)(a+b)=- ½ab + ½ab + ½ с2
а2 + b2 = с2
Доказательство закончено.

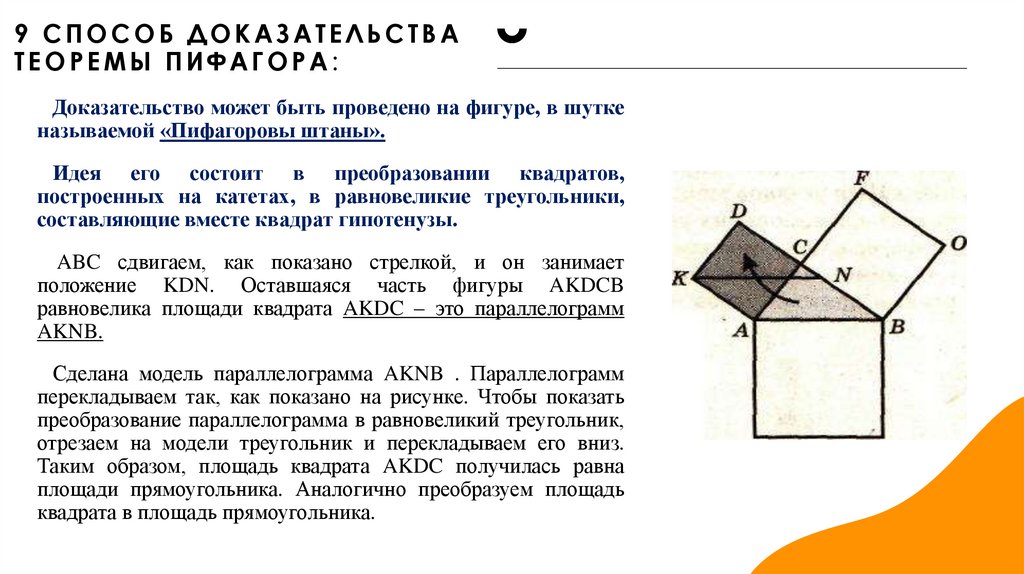
13. 9 способ доказательства теоремы Пифагора:

9 СПОСОБ ДОКАЗАТЕЛЬСТВА
ТЕОРЕМЫ ПИФАГОРА:
Доказательство может быть проведено на фигуре, в шутке
называемой «Пифагоровы штаны».
Идея его состоит в преобразовании квадратов,
построенных на катетах, в равновеликие треугольники,
составляющие вместе квадрат гипотенузы.
ABC сдвигаем, как показано стрелкой, и он занимает
положение KDN. Оставшаяся часть фигуры AKDCB
равновелика площади квадрата AKDC – это параллелограмм
AKNB.
Сделана модель параллелограмма AKNB . Параллелограмм
перекладываем так, как показано на рисунке. Чтобы показать
преобразование параллелограмма в равновеликий треугольник,
отрезаем на модели треугольник и перекладываем его вниз.
Таким образом, площадь квадрата AKDC получилась равна
площади прямоугольника. Аналогично преобразуем площадь
квадрата в площадь прямоугольника.

14. 2.1 Исследование знаний о теореме.

2.1 ИССЛЕДОВАНИЕ
ЗНАНИЙ О ТЕОРЕМЕ.
Как Вы думаете, в какой области
можно применять теорему Пифагора?
Знаете ли вы теорему
Пифагора?
20
15
10
5
0
Знаете ли
вы
теорему
Пифагора
?
при решении
геометрических
задач
в строительстве
в архитектуре
в инженерии
в искусстве
В школьном курсе геометрии с помощью теоремы Пифагора решаются только математические задачи. К
сожалению, вопрос о практическом применении теоремы рассматривается крайне редко. Теорема Пифагора
самая известная теорема в геометрии, о ней знает подавляющее большинство населения планеты. В связи с
этим, мне стало интересно проанализировать знания по этому вопросу среди своих сверстников. Я провела в
школе опрос на тему: «Знаете ли Вы теорему Пифагора?» Были получены следующие результаты:
Мое исследование показало, что учащиеся в большинстве знают теорему Пифагора, а вот в каких областях
нашей жизни ее можно применить… список ответов на этот вопрос оказался крайне скудным. Поэтому меня
заинтересовал вопрос практического применения теоремы. Для того чтобы ответить на этот вопрос, мне
пришлось обратиться к различным источникам.
в информатике
не знают

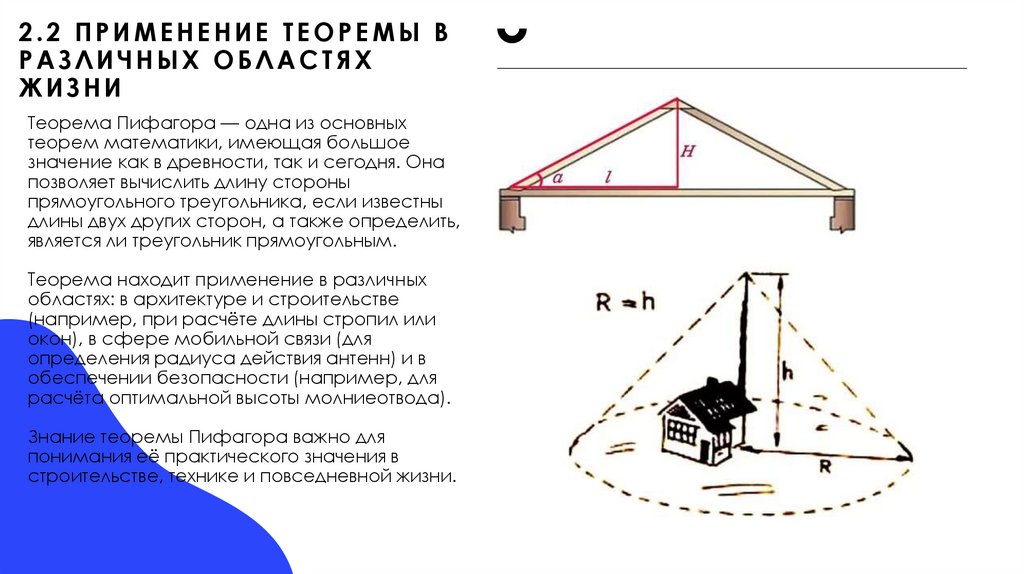
15. 2.2 Применение теоремы в различных областях жизни

2.2 ПРИМЕНЕНИЕ ТЕОРЕМЫ В
РАЗЛИЧНЫХ ОБЛАСТЯХ
ЖИЗНИ
Теорема Пифагора — одна из основных
теорем математики, имеющая большое
значение как в древности, так и сегодня. Она
позволяет вычислить длину стороны
прямоугольного треугольника, если известны
длины двух других сторон, а также определить,
является ли треугольник прямоугольным.
Теорема находит применение в различных
областях: в архитектуре и строительстве
(например, при расчёте длины стропил или
окон), в сфере мобильной связи (для
определения радиуса действия антенн) и в
обеспечении безопасности (например, для
расчёта оптимальной высоты молниеотвода).
Знание теоремы Пифагора важно для
понимания её практического значения в
строительстве, технике и повседневной жизни.

16. Заключение

ЗАКЛЮЧЕНИЕ
В ходе исследования была достигнута цель
— расширение знаний о доказательстве
теоремы Пифагора. Изучены различные
методы её доказательства, что углубило
понимание темы.
Собранные материалы подтверждают, что
теорема Пифагора является выдающейся в
геометрии и имеет значительное значение.
Популярность теоремы обусловлена её
красотой, простотой и важностью!
Теорема имеет огромное практическое
значение: она применяется в нашей жизни
буквально везде. В своём проекте я показала
связь между теоремой Пифагора и другими
дисциплинами; её практическую значимость.
Попыталась
собрать
и
обобщить
информацию по данной теме. Я считаю, что
проведя такую большую работу, я достигла
своей цели и думаю, что результаты моей
работы будут полезны и интересны моим
сверстникам и всем школьникам.

17. Источники

И С ТОЧ Н И К И
1. Геометрия. 7-9 класс. Учебник, авторы Атанасян
Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
2.-Геометрия. Учебник для 7-9 классов, автор
Погорелов А.В.
3. Еленьский Ш. По следам Пифагора. М., 1961.
4. Литцман В. Теорема Пифагора. М., 1960.
5. Энциклопедия. Я познаю мир. Математика. – М.:
ООО «Издательство АСТ», 2003. – 408 с.
6. https://ru.wikipedia.org/wiki/Теорема_Пифагора
7. https://ru.wikipedia.org/wiki/Пифагор
8. https://blog.tutoronline.ru/teorema-pifagora
9. http://www.zaitseva-irina.ru/html/f1103454849.html