Числовые промежутки

1.

Числовые промежутки

2.

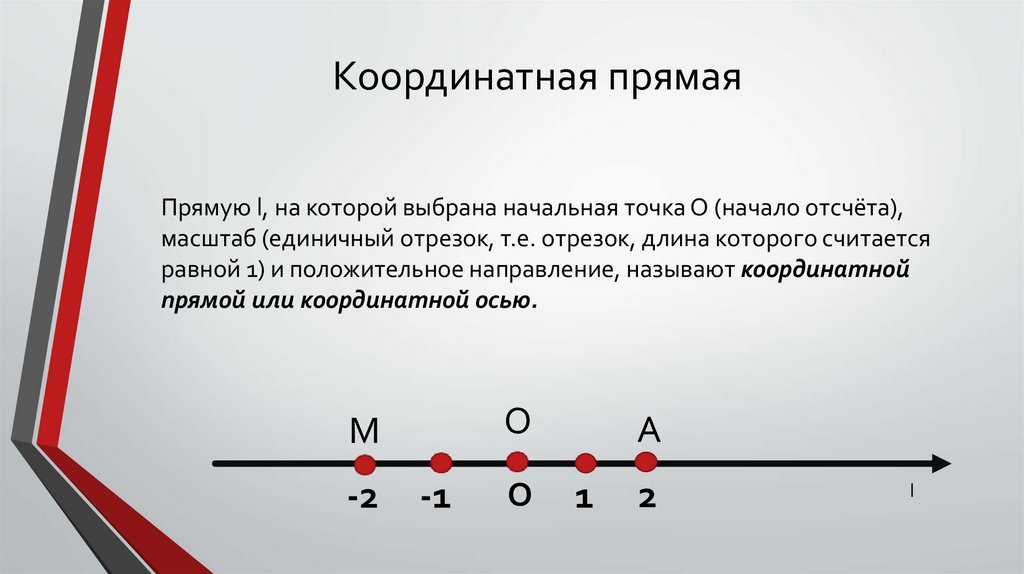
Координатная прямая
Прямую l, на которой выбрана начальная точка О (начало отсчёта),
масштаб (единичный отрезок, т.е. отрезок, длина которого считается
равной 1) и положительное направление, называют координатной
прямой или координатной осью.
O
М
-2
-1
О
А
1
2
l

3.

Каждому числу на координатной прямой соответствует единственная точка
O
Числу 2 соответствует точка А, которая удалена от начала отсчёта,
т.е. от точки О, на расстояние, равное 2 (в заданном масштабе), и
отложена от точки О в заданном (положительном) направлении.
Числу −2 соответствует точка М, которая удалена от начала отсчёта,
т.е. от точки О, на расстояние, равное 2 (в заданном масштабе), и
отложена от точки О в отрицательном направлении, т.е. в
направлении, противоположном заданному.
Указанные числа называют координатами соответствующих точек

4.

E
H
-4 -3 -2 -1 0
• Какую координату имеет точка H ?
• Какую координату имеет точка D ?
• Какую координату имеет точка E ?
• Какую координату имеет точка K ?
D
K
1 2
3 4
Х

5.

Расстояние между точками
Чтобы найти расстояние d от точки A до точки К достаточно воспользоваться
формулой: АК=|а-к|
Тогда например:
AK=|-3-4|=|-7|=7
EH=|-4-(-1)|=|-3|=3
Стремясь к лаконичности рассуждений, математики договорились
рассматриваемую точку обозначать ее координатой. Так на координатной
прямой расположены точки: -4;-3;-1;1;4.
А

6.

G T
H
S
Y
K
X
-8,25 -7,27
-3,2
0 1
4,11
9,15
14,2
Найдите расстояние между точками:
a) G и K
b) Y и H
c) T и S
d) K и X
e) G и T
17,4
7,31
7,27
5,05
0,98
В

7.

Открытый Луч
Пусть на координатной прямой отмечена точка а. Рассмотрим все точки,
расположенные правее точки a и отметим соответствующую часть
координатной прямой штриховкой.
а
Х
Это множество точек (чисел) называют открытым лучом и обозначают (a;+∞) ,
где знак +∞ читается как « плюс бесконечность».
Оно характеризуется неравенством x>a, где x - любая точка открытого луча.
Точка а не принадлежит открытому лучу и поэтому обозначается белой
(выколотой) точкой.

8.

Пусть на координатной прямой отмечена точка b. Рассмотрим все точки,
расположенные левее точки b и отметим соответствующую часть
координатной прямой штриховкой.
b
Х
Это множество точек (чисел), так же называют открытым лучом и
обозначают (-∞; b) , где знак -∞ читается как «минус бесконечность».
Оно характеризуется неравенством x<a, где x - любая точка открытого
луча.
Точка b, так же не принадлежит открытому лучу и следовательно
обозначается белым (выколотым) кружком (точкой).

9.

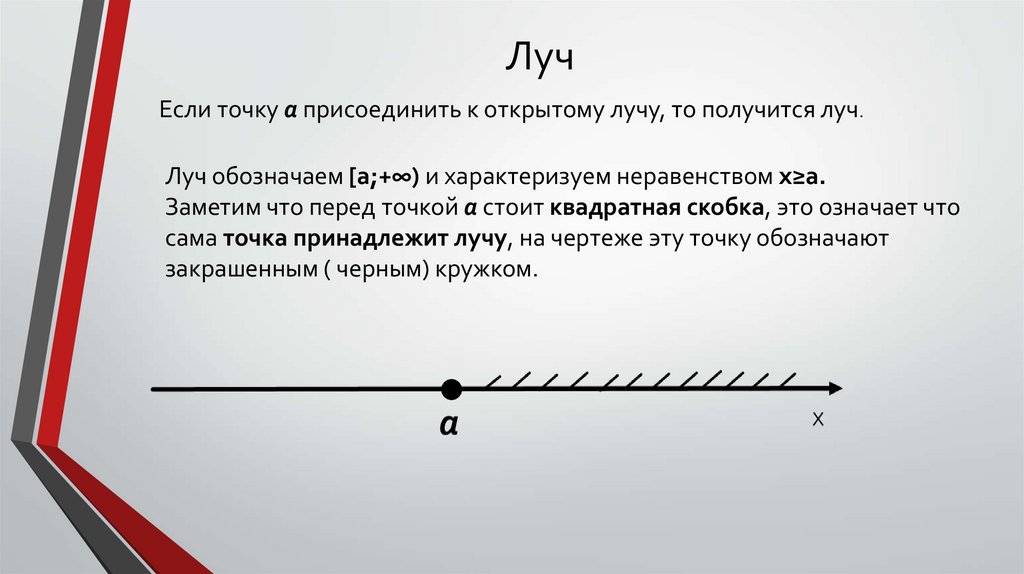
Луч
Если точку a присоединить к открытому лучу, то получится луч.
Луч обозначаем [a;+∞) и характеризуем неравенством x≥a.
Заметим что перед точкой а стоит квадратная скобка, это означает что
сама точка принадлежит лучу, на чертеже эту точку обозначают
закрашенным ( черным) кружком.

10.

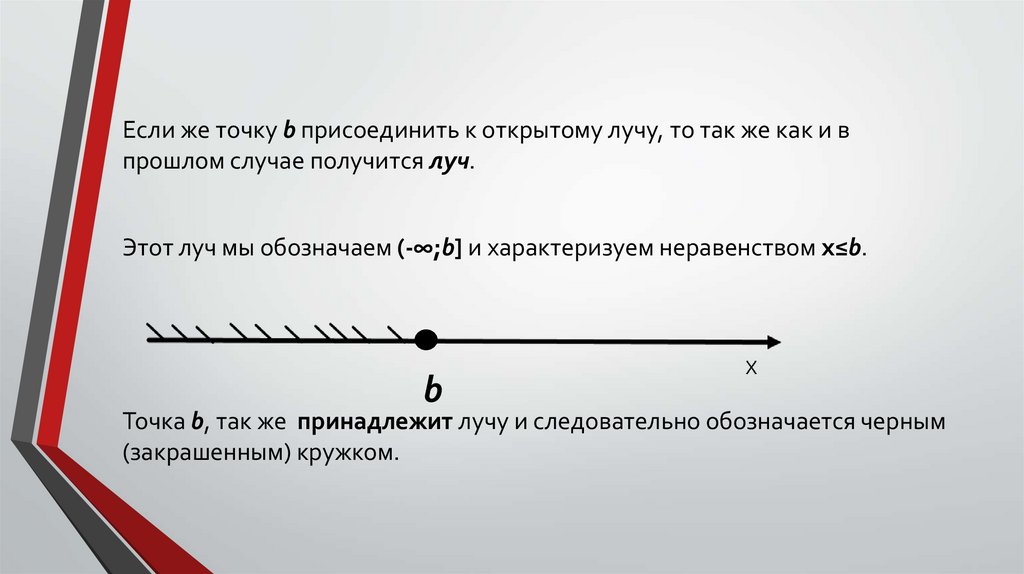
Если же точку b присоединить к открытому лучу, то так же как и в
прошлом случае получится луч.
Этот луч мы обозначаем (-∞;b] и характеризуем неравенством x≤b.
b
Точка b, так же принадлежит лучу и следовательно обозначается черным
(закрашенным) кружком.

11.

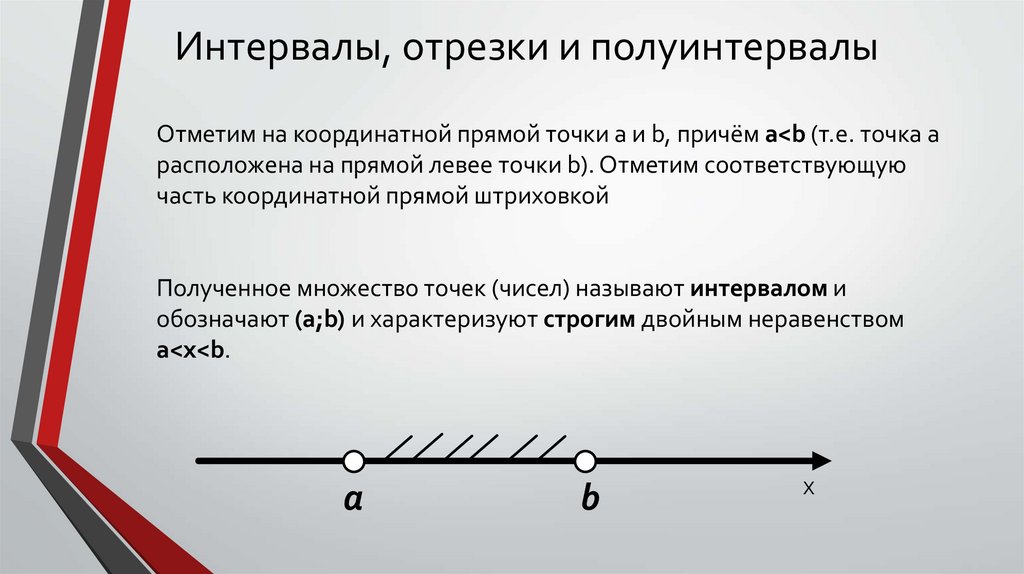
Интервалы, отрезки и полуинтервалы
Отметим на координатной прямой точки a и b, причём a<b (т.е. точка a
расположена на прямой левее точки b). Отметим соответствующую
часть координатной прямой штриховкой
Полученное множество точек (чисел) называют интервалом и
обозначают (a;b) и характеризуют строгим двойным неравенством
a<x<b.
a
b
Х

12.

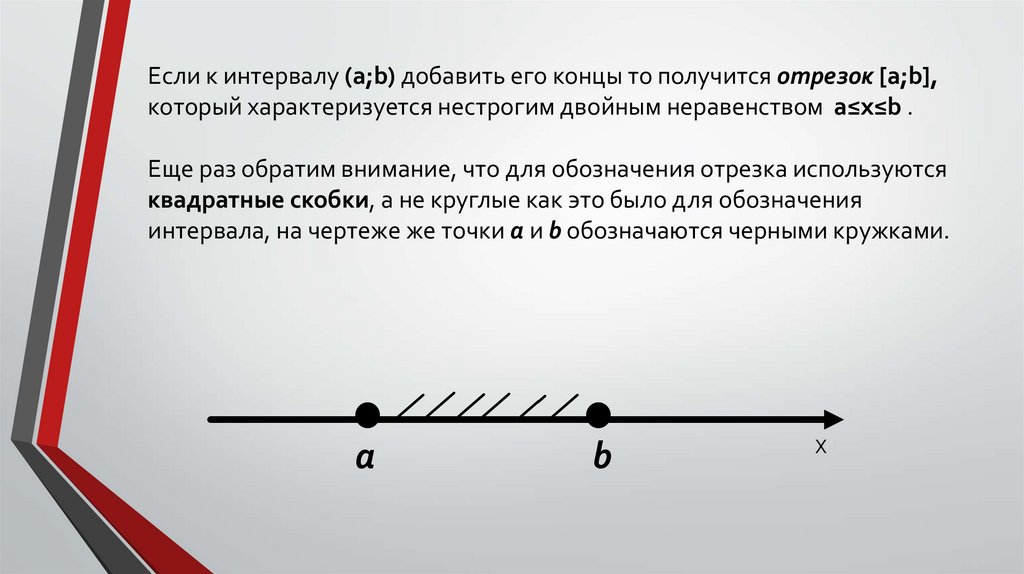
Если к интервалу (a;b) добавить его концы то получится отрезок [a;b],
который характеризуется нестрогим двойным неравенством a≤x≤b .
Еще раз обратим внимание, что для обозначения отрезка используются
квадратные скобки, а не круглые как это было для обозначения
интервала, на чертеже же точки a и b обозначаются черными кружками.

13.

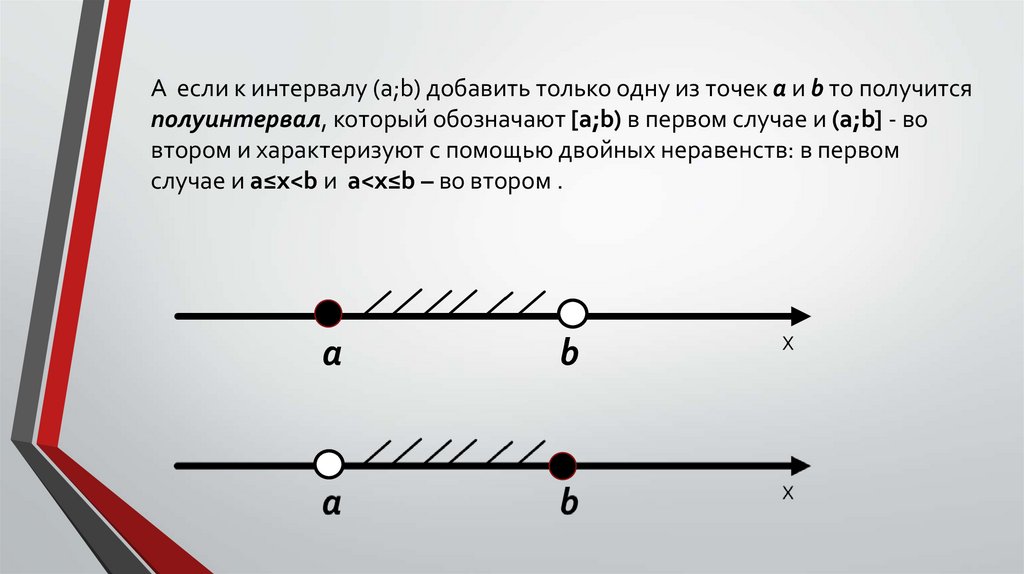
А если к интервалу (a;b) добавить только одну из точек a и b то получится
полуинтервал, который обозначают [a;b) в первом случае и (a;b] - во
втором и характеризуют с помощью двойных неравенств: в первом
случае и a≤x<b и a<x≤b – во втором .

14.

Итак, введены пять новых терминов: луч, открытый луч, интервал, отрезок,
полуинтервал. Общее их название - числовые промежутки.
К слову, сама координатная прямая также является числовым
промежутком, который обозначают (−∞;+∞)

15.

Упражнения
По геометрической модели определите название числового промежутка,
обозначьте его и укажите аналитическую модель
3
Открытый луч
(3;+∞)
Х> 3
луч
(-∞;100]
Х≤100
полуинтервал
(7;87]
7<Х≤87
полуинтервал
[-8;-1)
-8≤Х<-1
Х
100
Х
7
87 Х
-8
-1
У

16.

Сколько целых чисел принадлежат промежуткам:
(5;9)
3
[0;3)
3
(7;8]
1
[110;112)
2
[-1;8]
10
[7,57;12,8]
5
[54;56]
3
(54,435;67,66666]
13

17.

Какие из чисел принадлежат
промежутку (3;96] ?
Какие из чисел принадлежат
промежутку (-17;+∞) ?
a)3
b)5
c)7
d)90
e)60
f) 234
g)7890
h)12
i) 4
j) 96
a)7
b)-1
c)-12
d)-45
e)0
f) 4567
g)100
h)-101
i) 34
j) -88