Статически неопределимые балки

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Лекция 4.
Статически неопределимые балки.
Авторы:
к.т.н., Войтко Александр Михайлович
1

2.

Статически неопределимые балки и рамы – конструкции, в которых уравнений статики
недостаточно для определения опорных реакций и внутренних усилий. Число связей,
наложенных на статически неопределимую систему, больше того количества связей, которые
обеспечивают геометрическую неизменяемость конструкции.
Дополнительные связи, которые не являются необходимыми для обеспечения
геометрической неизменяемости конструкции, называются лишними.
Перед расчетом статически неопределимой конструкции необходимо сначала определить
степень статической неопределимости рассматриваемой системы. Для балок и
простых рам степень статической неопределимости равна числу лишних опорных связей
2

3.

Алгоритм решения задач методом сил:
1). Определить степень статической неопределимости.
2). Записать систему канонических уравнений.
3). Выбрать основную систему.
4). Построить эпюры в основной системе от единичных сил и нагрузки.
5). Определить коэффициенты (δ11 , δ12, δ22) и свободные члены(∆1F и ∆2F) канонических уравнений
метода сил по формуле Мора.
6). Решить канонические уравнения. Определить неизвестные.
7). Построить эпюры от найденных неизвестных: М1х1, М2х2 …в основной системе.
8). Построить окончательную эпюру моментов М в заданной системе.
9). Построить эпюру поперечных сил.
10). Определить опорные реакции.
11). Выполнить статическую проверку.
3

4.

Для уменьшения в системе уравнений количества неизвестных, которые определяются в
первую очередь, при расчете балок и рам чаще всего используют прием, связанный с выбором
основной системы.
Основная система – это статически определимая конструкция, полученная из заданной
системы путем отбрасывания лишних связей. Реакции в отброшенных связях принято называть
лишними неизвестными и обозначать Хi.
или
1). Определим степень статической неопределимости: nст. = 4 - 3 = 1.
2). Имеется одна лишняя связь. Её надо удалить, чтобы получить статически определимую балку.
Удалим правую горизонтальную опору и заменим её реакцией х1, пока ещё неизвестной.
х1 – реакция первой (в нашем случае и единственной отброшенной
связи).
4

5.

Основная система метода сил (ОСМС) должна быть статически определимой и геометрически
неизменяемой
3). Точка 1 (правая опора) под действием силы F переместилась вправо.
∆1F – перемещение от нагрузки по направлению первой отброшенной связи (вспомним: 1-й индекс
– место, 2-й индекс – причина).
Его можно найти по формуле Мора
4). Точка 1 под действием силы х1 переместилась влево. Но х1 нам
неизвестен и поэтому перемещение от х1 нам не определить.
Поэтому мы зададим ему единичное безразмерное значение и
по формуле Мора определим единичное перемещение δ11 от х1 = 1
по направлению первой отброшенной связи х1.
5

6.

Тогда перемещение от реальной х1 будет в х1 раз больше: δ11 х1
5). Поскольку точка 1 никуда не перемещалась, то будет справедливо равенство:
δ11 х1 + ∆1F = 0
Это уравнение называется каноническим уравнением метода сил для nст. = 1.
Его физический смысл: Сумма перемещений по направлению отброшенной связи от всех силовых
факторов равна нулю.
Для nст. = 2 - будет система из двух уравнений:
δ11 х1 + δ12 х2 + ∆1F = 0;
δ21 х1 + δ22 х2 + ∆2F = 0;
Для nст. = К
будет система К уравнений:
δ11 х1 + δ12 х2 + δ13 х3 + … + δ1К хК + ∆1F = 0;
δ21 х1 + δ22 х2 + δ23 х3 + … + δ2К хК + ∆2F = 0;
………………………….
ΔК1 х1 + δК2 х2 + δК3 х3 + … + δКК хК + ∆КF = 0;
6

7.

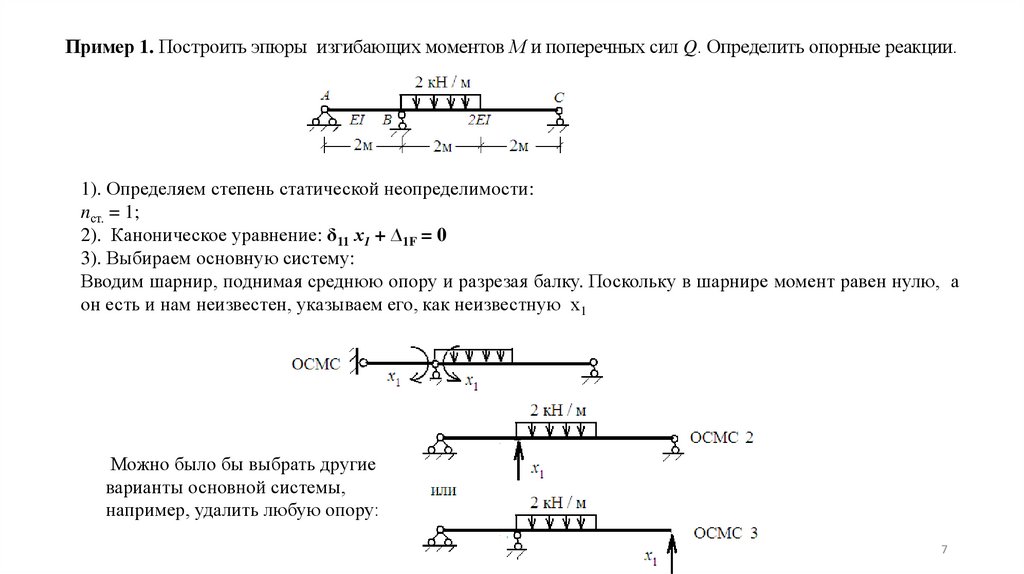
Пример 1. Построить эпюры изгибающих моментов М и поперечных сил Q. Определить опорные реакции.
1). Определяем степень статической неопределимости:
nст. = 1;
2). Каноническое уравнение: δ11 х1 + ∆1F = 0
3). Выбираем основную систему:
Вводим шарнир, поднимая среднюю опору и разрезая балку. Поскольку в шарнире момент равен нулю, а
он есть и нам неизвестен, указываем его, как неизвестную х1
Можно было бы выбрать другие
варианты основной системы,
например, удалить любую опору:
7

8.

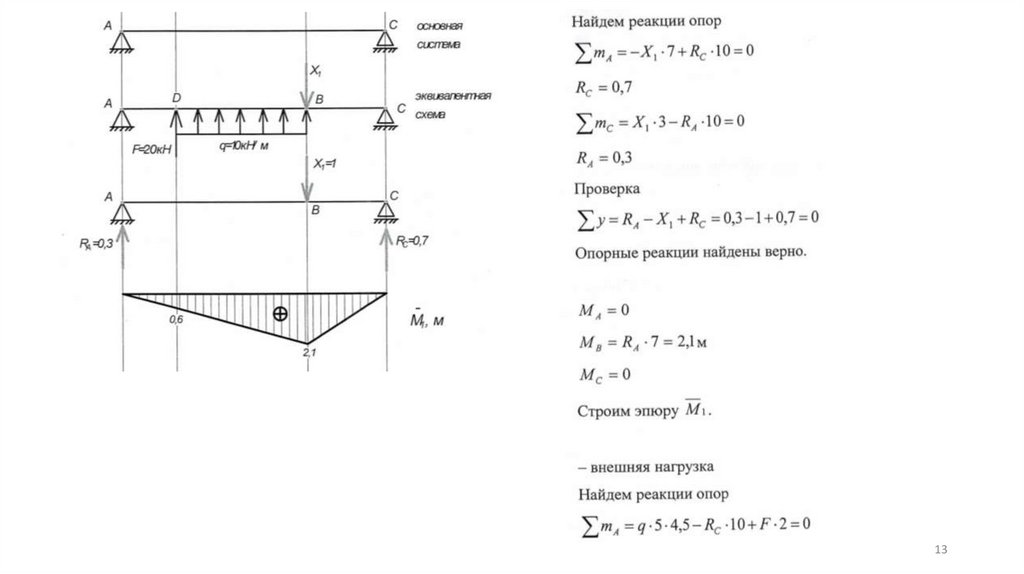
4). Строим эпюру в основной системе от единичной пары сил.
5). Строим эпюру моментов МFo в основной системе от нагрузки. Рассматриваем отдельно каждый
брус. Брус АВ не нагружен. Для бруса ВС сначала определяем опорные реакции.
8

9.

9

10.

9). Строим окончательную эпюру моментов М в заданной
системе, воспользовавшись принципом независимости
действия сил.
М = М1о·х1 + МFo
10

11.

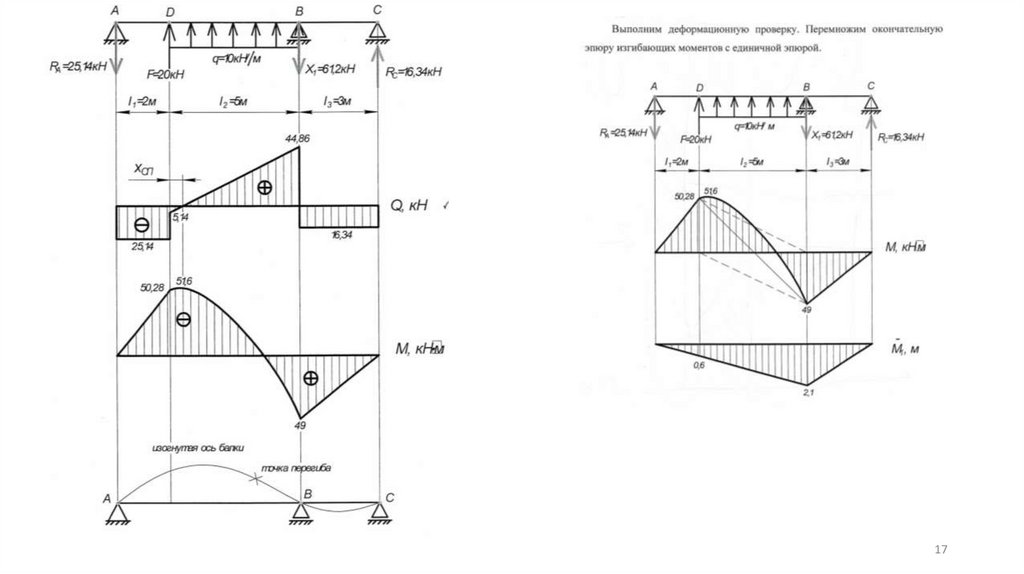
10). Определим опорные реакции. Для этого рассмотрим
равновесие вырезанных частей бруса.
11). Выполним статическую проверку:
∑ у = 3.84 + 0.72 - 0.56 - 2∙2 = 0;
∑ МА = - 3.84∙2 - 0.72∙6 + 2∙2∙3 = 0;
12). Определим экстремум параболы на эпюре моментов:
На эп. Q отметим сечение, где Q меняет знак (Q =0). Обозначим его х.
Найдём
Qх = - 0.72 + 2∙х = 0;
х = 0.36м;
Определим момент в этом сечении х:
Мех = 0.72 ∙ 2.36 - 2 ∙ 0.36 ∙ 0.18 = 1.57 кн ∙м.
11

12.

12

13.

13

14.

14

15.

15

16.

16

17.

17

18.

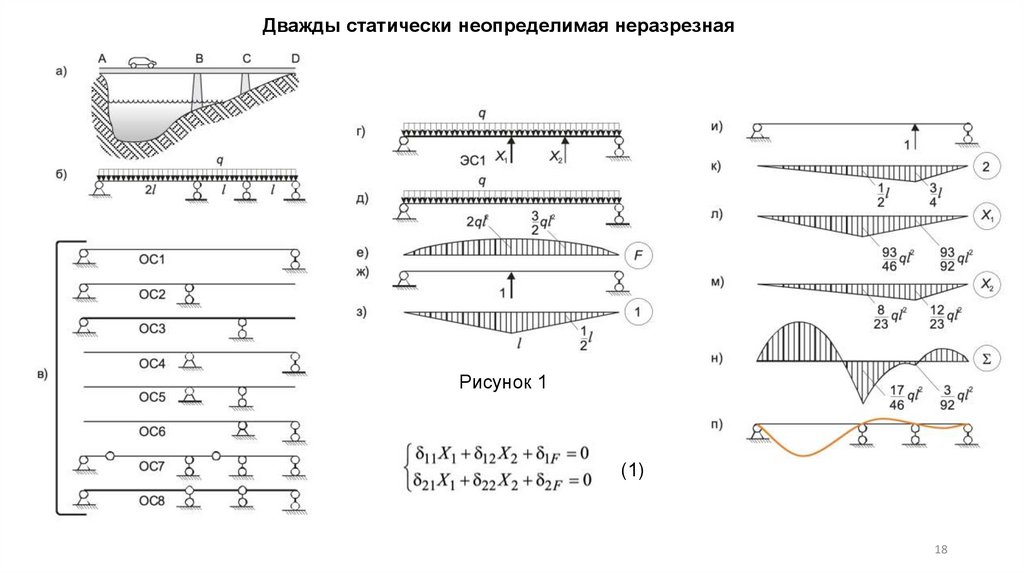
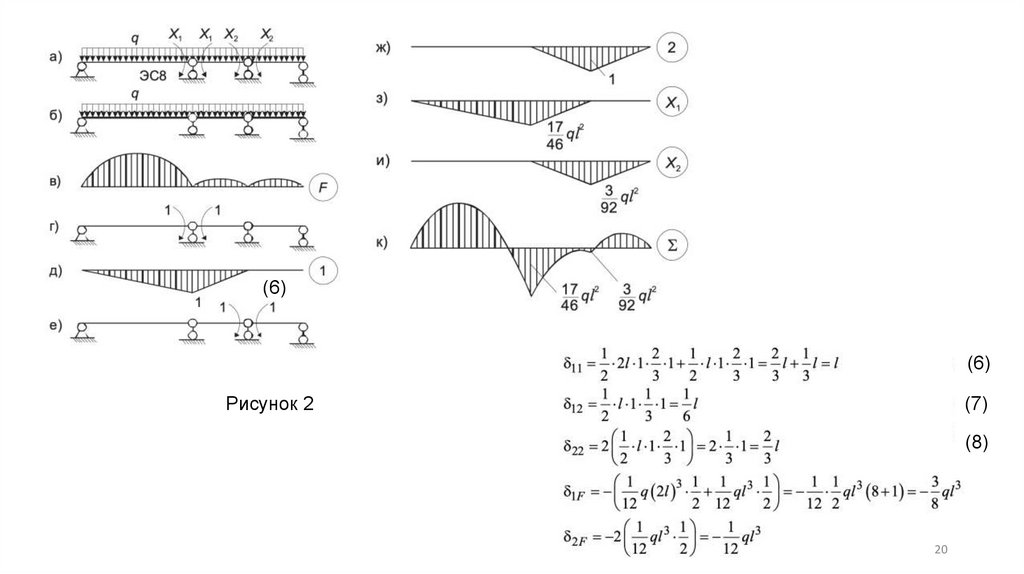
Дважды статически неопределимая неразрезная
балка
Рисунок 1
(1)
18

19.

(2)
(3)
(4)
(5)
19

20.

(6)
(6)
Рисунок 2
(7)
(8)
20

21.

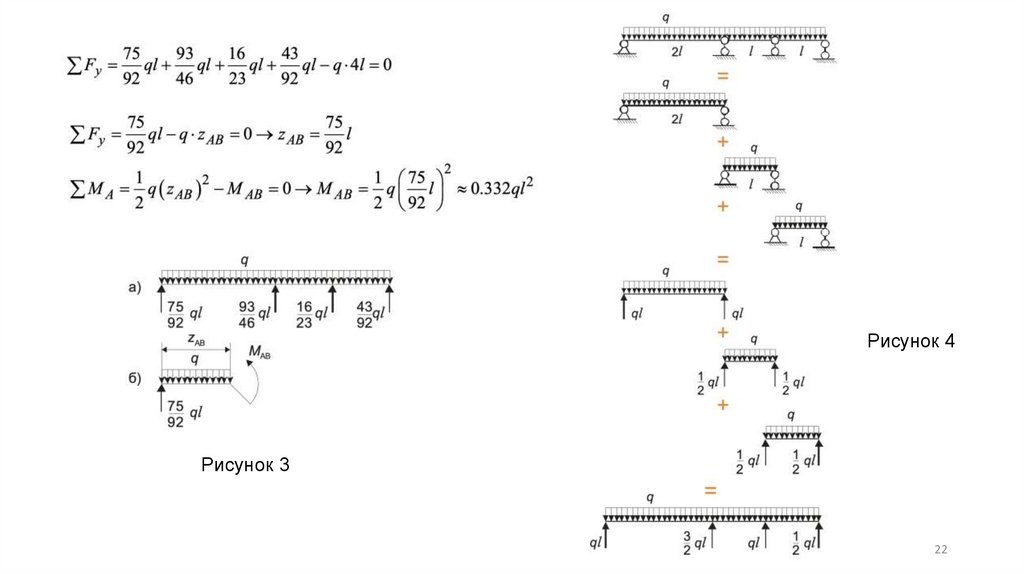
(10)
(9)
(11)
21

22.

Рисунок 4
Рисунок 3
22

23.

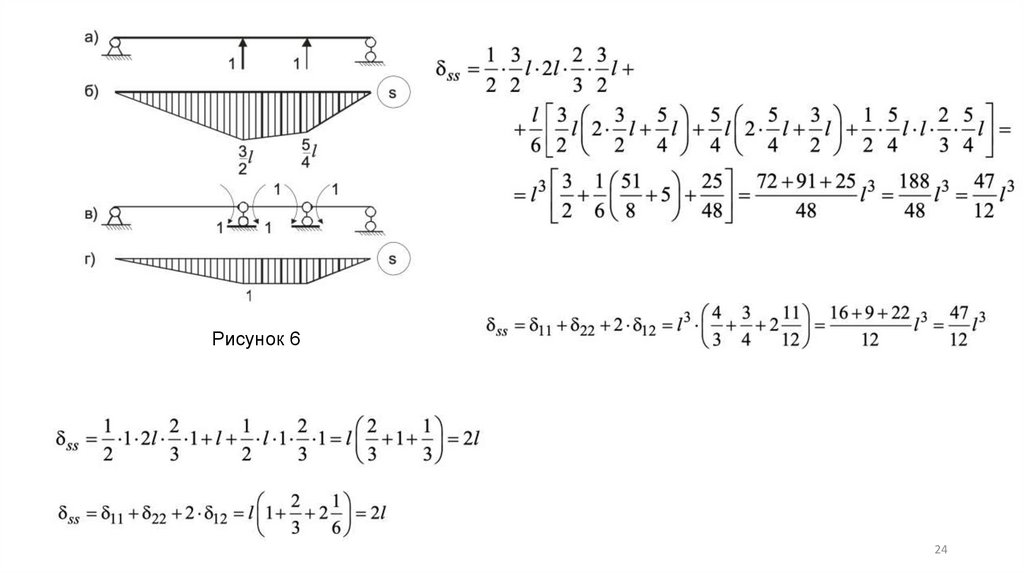
Рисунок 5
(12)
23

24.

Рисунок 6
24

25.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Авторы:
к.т.н., Войтко Александр Михайлович
[email protected]
25