Similar presentations:
Расчет статически неопределимых систем
1. Расчет статически неопределимых систем
2. Статически неопределимый брус (стержень)
Дан стержень, жестко закрепленный с двухконцов и нагруженный силами Р1 и Р2
Требуется определить опорные реакции и построить
эпюры внутренних сил, напряжений, относительных
деформаций и перемещений
3. Статически неопределимый стержень (продолжение)
Покажем опорные реакции и составимуравнение равновесия
X 0
-RA-P1+P2+RB=0
Получили одно уравнение с двумя неизвестными –
система статически неопределимая
4. Раскрытие статической неопределимости Для раскрытия статической неопределимости осуществляется переход к статически
определимому стержню, эквивалентномузаданному, путем отбрасывания одной лишней
связи, например, стенки В, замены действия ее
неизвестной силой Rb и составление уравнения
перемещения сечения В с учетом тех
ограничений, которые накладывались на
перемещение сечения В отброшенной связью.
В случае жесткой стенки UB=0
5. Есть два подхода к записи уравнения перемещений UB=0. Первый рассматривает перемещение UB как сумму накопленных деформаций
отдельных участков на всейдлине стержня.
UB=Δl1+Δl2+Δl3+Δl4+Δl(T)=0.
Таким образом, достаточно найти внутреннюю силу на
каждом участке, чтобы определить деформацию каждого
участка, т.к. остальные исходные данные нам известны.
Для этого удобно рассматривать ту отсеченную часть,
где представлена неизвестная сила RB.
6. Определение внутренних силовых факторов на каждом участке и запись уравнения перемещений
7. Второй подход к записи уравнения перемещений UB=0.
Используется принципнезависимости действия сил
где
8. Статически неопределимая стержневая система
;Статически неопределимая
стержневая система
.
X 0
Y 0
N AB N AC 0
N AB cos N AC cos P
9. Статически неопределимая стержневая система (продолжение)
.X 0
Y 0
N AB N AC 0
N AB cos N AC cos N AD P
10. Статически неопределимая стержневая система (продолжение 2)
.Статически неопределимая
стержневая система (продолжение 2)
l AB l AD cos
l AB
N ABl AB
E AB F
l AD l AB cos
N AB N AC
l AD
N ADl AD
E AD F
N AB N AD cos2
P cos 2
1 2 cos3
P
N AD
1 2 cos3
11. Механические свойства материалов при растяжении
PD0 10 мм
P
L0 100 мм
~140 мм
Образец для испытаний
L0 - расчетная длина, база измерений удлинения; Р – растягивающая сила,
D 2
F0
4
- начальная площадь поперечного сечения образца
12. Машина для испытаний материалов
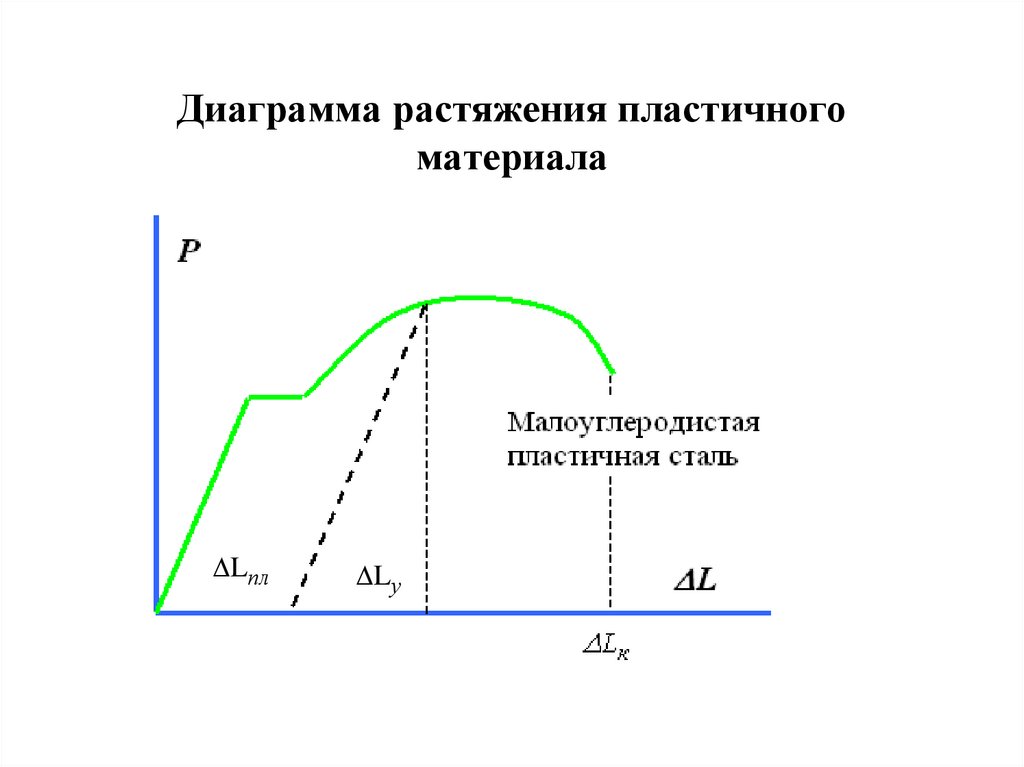
13. Диаграмма растяжения пластичного материала
LплLу
14. Диаграмма растяжения хрупкого материала
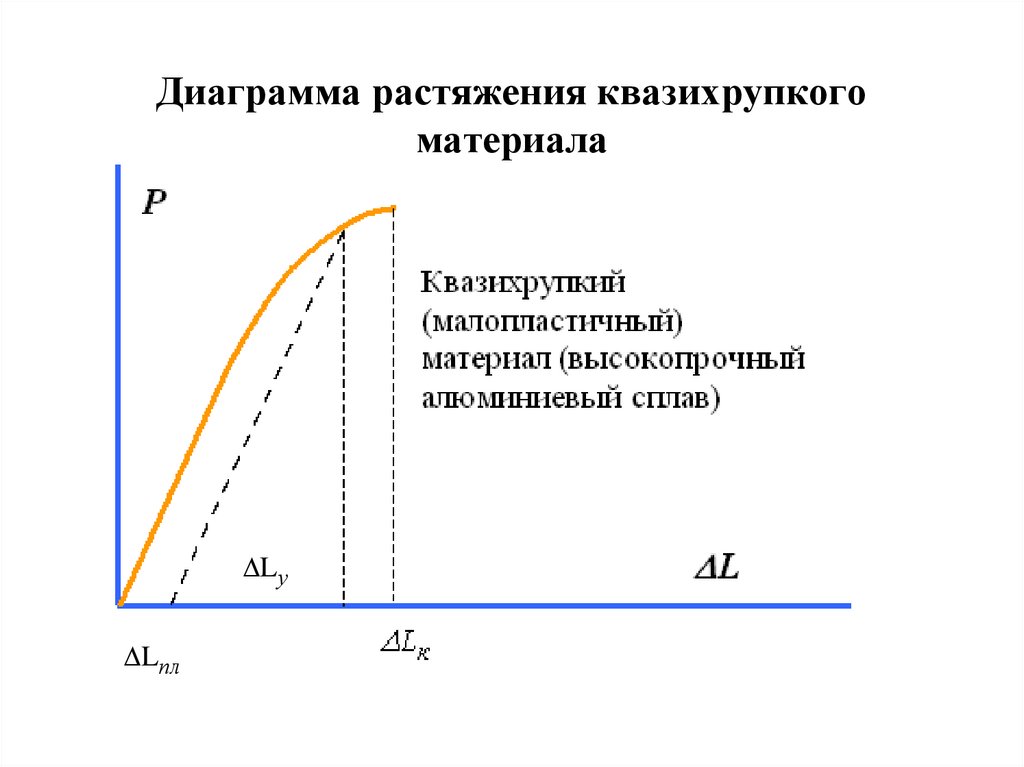
15. Диаграмма растяжения квазихрупкого материала
LуLпл
16. Определение модуля упругости
Py L0E
.
F0 L y
17. Определение предела текучести, предела прочности и истинного напряжения разрыва
PTT
F0
Pmax
b
F0
18. Определение предела пропорциональности, предела упругости и условного предела текучести
пцPпц
F0
0,05
P0,05
0,2
P0,2
F0
F0
19. Стадии деформации образца, относительное удлинение и относительное сужение
рLmax
L0
Lкпл
L0
F0 Fк
F0
Т
LT
Т
E
L0
20. Предельные характеристики материалов
• Предел текучести для пластичныхматериалов - σT
• Временное сопротивление или предел
прочности для хрупких материалов - σB
• Расчетная характеристика – допускаемое
напряжение [σ]
21. Жесткость и податливость стержня
Произведение модуля упругости на площадь поперечногосечения ЕF называю жесткостью поперечного сечения стержня
при растяжении.
Жесткость ЕF поперечного сечения, деленную на длину L
стержня
EF
k
,
L
называют жесткостью стержня.
Величину , обратную жесткости k
1
,
k
называют податливостью стержня.
Для стержня длиной L, нагруженного продольными силами P,
имеют место следующие зависимости между силой P и удлинением
:
P k
и
P .
22. Испытание на сжатие Особенности испытания на сжатие
• Трудно обеспечить соосность нагружения• Длинные образцы теряют устойчивость
• Чем меньше отношение длины образца к его
диаметру, тем заметнее влияние трения на
торцах образца, которое приводит к
образованию бочкообразной формы образца из
пластичных материалов
• По той же причине образцы из пластичных
материалов нельзя довести до разрушения
23. Механические характеристики, определяемые при испытании хрупких и пластичных материалов на сжатие по ГОСТ 25.503
• ГОСТом предусматривается по результатамиспытаний образцов на сжатие определение
следующих механических характеристик: модуля
упругости, предела пропорциональности, предела
упругости, физического предела текучести, условного
предела текучести, предела прочности
• испытывают цилиндрические образцы четырех типов:
с гладкими торцами (три типа) и торцевыми
выточками
24. Механические характеристики, определяемые при испытании хрупких и пластичных материалов на сжатие по ГОСТ 25.503
• По результатам испытания строится диаграмма сжатияв координатах сжимающая нагрузка Р – укорочение
образца ∆h
• Процедура определения прочностных характеристик
при сжатии практически не отличается от процедуры
их определения при растяжении
• Сопоставление диаграмм растяжения и сжатия
пластичных материалов показывает, что на начальной
стадии деформирования эти диаграммы совпадают и
характеристики сопротивления начальным
пластическим деформациям (σпц, σ0,05, σт, σ0,2)
практически одинаковы
25. Сравнение диаграмм растяжения и сжатия пластичного материала
26. Сравнение диаграмм растяжения и сжатия пластичного материала
• При развитых пластических деформациях вид кривойсжатия существенно отличается от характера кривой
растяжения. Кривая сжатия идет выше, круче. Она не
обрывается, поскольку невозможно довести образец до
разрушения.
• Диаграмма сжатия пластичного материала должна
быть ограничена величиной максимальной
деформации, при которой еще испытывается материал
образца, а не захватных приспособлений
испытательной машины


























 mechanics
mechanics








