Сопротивление материалов. Основные положения. Гипотезы и допущения

1.

Раздел
Сопротивление материалов

2.

Сопротивление материалов
Тема Основные положения. Гипотезы и
допущения
Раздел технической механики, в котором
представлены методы расчета элементов
конструкций на прочность, жесткость и
устойчивость

3.

Механические свойства материалов
Прочность – способность не разрушаться под
нагрузкой
Жесткость – способность незначительно
деформироваться под нагрузкой
Выносливость – способность длительное
время выдерживать переменные нагрузки
Вязкость – способность воспринимать ударные
нагрузки

4.

Расчет на прочность обеспечивает: неразрушение материалов
Расчет на жесткость обеспечивает: деформации конструкций
под нагрузкой в пределах допустимых нор
Расчет на выносливость обеспечивает: необходимую
долговечность элементов конструкций
Расчет на устойчивость обеспечивает: сохранение
необходимой формы равновесия и предотвращает внезапное
искривление длинных стержней
Расчеты на удар обеспечивают: прочность конструкций ,
работающих на удар
• Задачи

5.

Основные гипотезы и допущения
Допущения о свойствах:
Материалы однородны (одинаковые физико-механические свойства)
Материалы – сплошная среда (не учитывается кристаллическое
строение и микроскопические дефекты)
Материалы изотропны (механические свойства не зависят от
направления нагрузки)
Материалы обладают идеальной упругостью
Допущения о характере деформаций:
- Перемещение точек тела, обусловленные его упругими
деформациями, весьма малы по сравнению с размерами тела.
- Перемещение точек упругого тела в известных пределах
нагружения прямо пропорциональны силам, вызывающим
эти перемещения.

6.

Классификация нагрузок и элементов
конструкций
Статические (не меняются или меняются
медленно)
Под действием статических нагрузок проводят расчет на прочность
Повторно-переменные (многократно меняют
значение или знак)
Действие вызывает усталость
Динамические (меняют значение в короткий
промежуток)
Вызывают большие ускорения и силы инерции и могут привести к
внезапному разрушения

7.

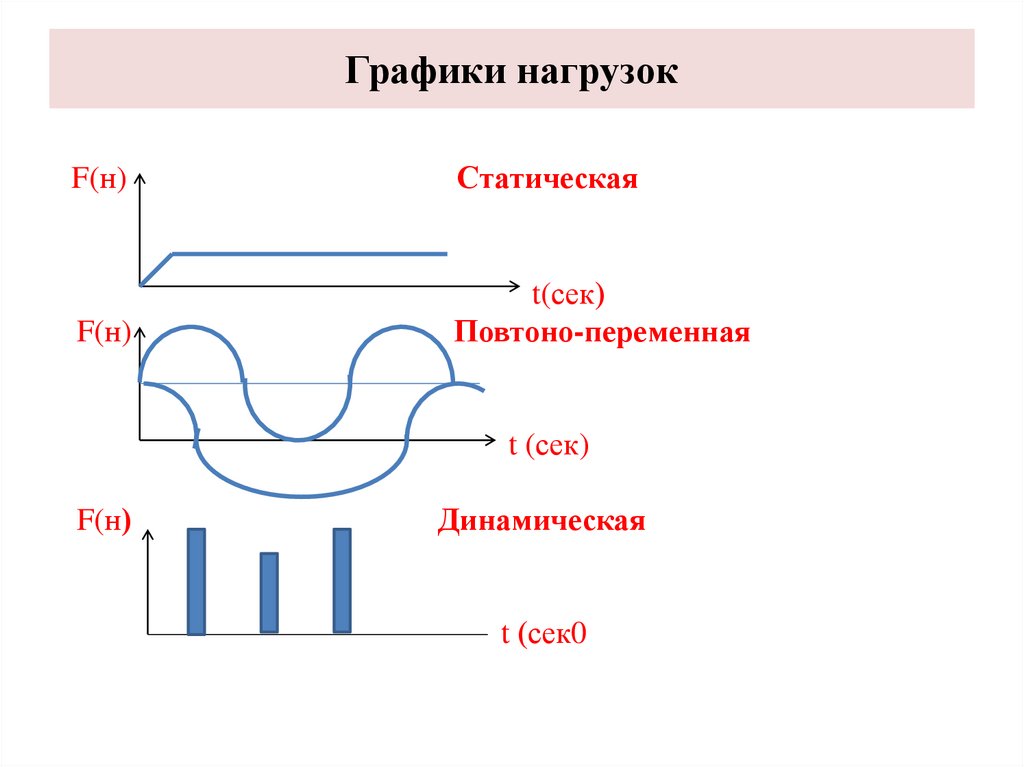
Графики нагрузок
F(н)
Статическая
F(н)
t(сек)
Повтоно-переменная
t (сек)
F(н)
Динамическая
t (сек0

8.

Формы элементов конструкций
Брус (длина значительно больше других размеров).
Прямой постоянного
сечения
Прямой ступенчатый
Криволинейный
Пластина (толщина значительно меньше других размеров)
Массив (тело у которого все размеры одного порядка)

9.

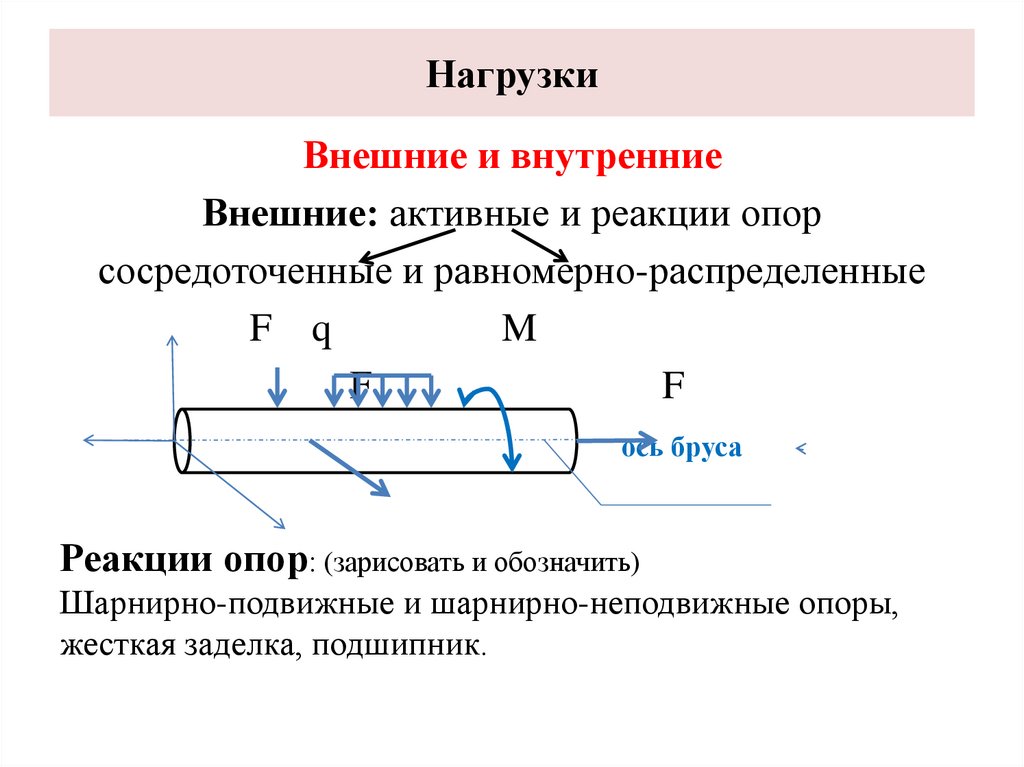
Нагрузки
Внешние и внутренние
Внешние: активные и реакции опор
сосредоточенные и равномерно-распределенные
F q
M
F
F
F
ось бруса
Реакции опор: (зарисовать и обозначить)
Шарнирно-подвижные и шарнирно-неподвижные опоры,
жесткая заделка, подшипник.

10.

Тема Метод сечений. Напряжения
Метод сечений используют для определения внутренних
усилий по заданным внешним силам.
Метод сечений заключается в мысленном рассечении
тела плоскостью и рассмотрение равновесия
любой из отсеченных частей. (если все тело в равновесии, то
и каждая его часть в равновесии)
В зависимости от действия внешних сил деформации
бывают:
Растяжение – сжатие
Кручение
Изгиб
Сложные (сочетание простейших)

11.

Реакции опор
Yа
Yа
Yа
Xа
А
А
Xa
А
Ma
Za
А
Xa
Ось бруса – геометрическое место центров тяжести его
поперечных сечений

12.

В зависимости от действия внешних сил в любом
поперечном сечении возникает
главный вектор и главный момент внутренних сил
Составляющие главного вектора и главного момента
внутренних сил называются – внутренние силовые
факторы или внутренние усилия:
Nz- продольная сила (н)
Qx, Qy – поперечные силы (н)
Mx, My – изгибающие моменты (нм)
Mz - крутящий момент (нм)
Для определения каждого нужно составлять уравнения
равновесия

13.

Растяжение-сжатие
Схема расчетная
F1
F2
F3
Z
X
Y
∑проекций сил на ось Z =Nz+∑Fi=0
Отс.части
Продольная сила в произвольном сечении бруса равна
алгебраической сумме проекций всех внешних сил,
приложенных к отсеченной части на ось Z
Nz=∑Fi
Nz

14.

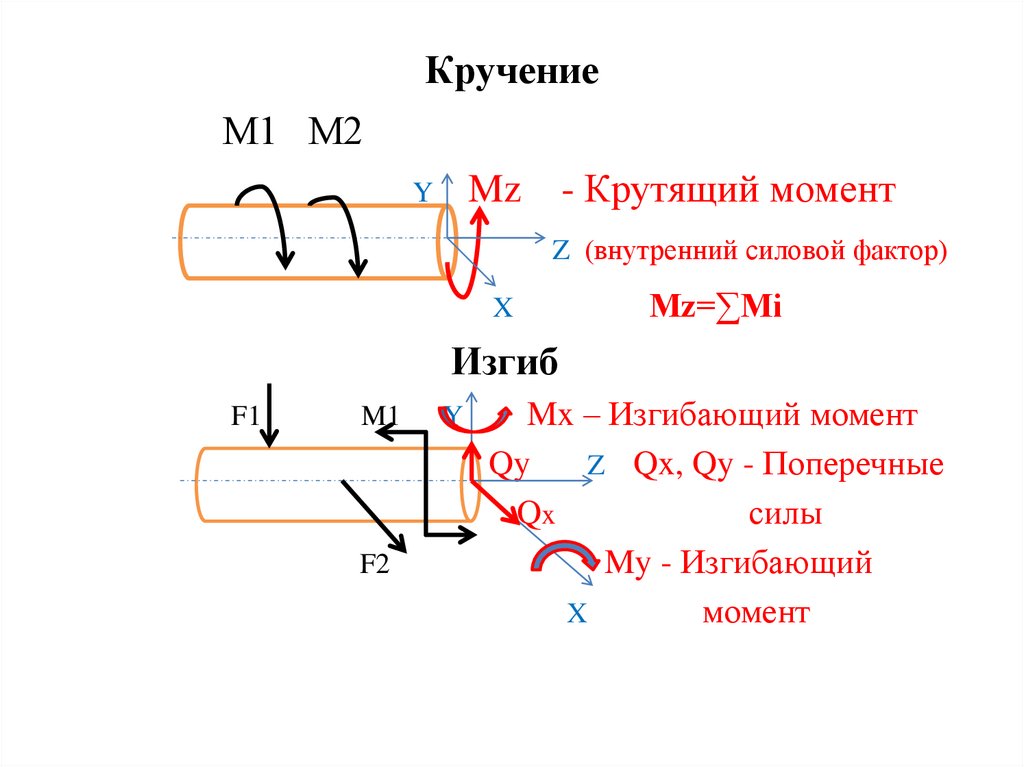
Кручение
М1 М2
- Крутящий момент
Mz
Y
Z (внутренний силовой фактор)
X
Мz=∑Mi
Изгиб
F1
M1
F2
Y
Mx – Изгибающий момент
Qy
Z Qx, Qy - Поперечные
Qx
силы
My - Изгибающий
X
момент

15.

Напряжения
Внутренние усилия распределены по всему сечению
бруса
Интенсивность внутренних сил в точке поперечного
сечения – механическое напряжение
Pср
τ (касательное)
σ
(нормальное)
Рср – полное напряжение ( Па=н/мм²)
τ – касательное (от Qx ,Qy, Mz)
σ- нормальное (Nz, Mx,My)
P=√σ²+τ²

16.

Например при растяжении – сжатии
σ= Nz/А, где А – площадь сечения
При кручении
τ=Мz/Wρ, где Wρ – полярный момент
сопротивления сечения
При изгибе
σ= Мx/ Wx, где Wx – осевой момент инерции сечения

17.

Растяжение - сжатие
Растяжением – сжатием, называется вид деформации
(нагружения) при котором в поперечном сечении бруса
возникает один внутренний силовой фактор – Продольная
сила (Nz).
Продольная сила меняется по длине бруса в зависимости от
расположения внешних сил.
Эпюра – график, показывающий изменение силового
фактора по длине бруса.
Так как Nz=∑Fi , то если
Отс.части
Nz
F- растягивает
Nz
F – сжимает
Nz + (положительно),
Nz – (отрицательно)

18.

Построение эпюр Nz и σ
Алгоритм:
1. Построение ведем от начала (свободного конца
бруса)
2.Делим брус на участки в зависимости от
расположения внешних сил и обозначаем сечения
цифрами 1,2,…
3. Для каждого участка составляем уравнение
равновесия;
4. Вычисляем Nz1, Nz2, …..
5. Строим ось бруса (нулевая линия), сверху
откладываем положительные значения Nz , снизу
отрицательные

19.

Напряжения при растяжении сжатии
σ=Nz/A
Н/м² =1 Па,
Где Nz- продольная сила на каждом участке
А- площадь сечения бруса на каждом участке

20.

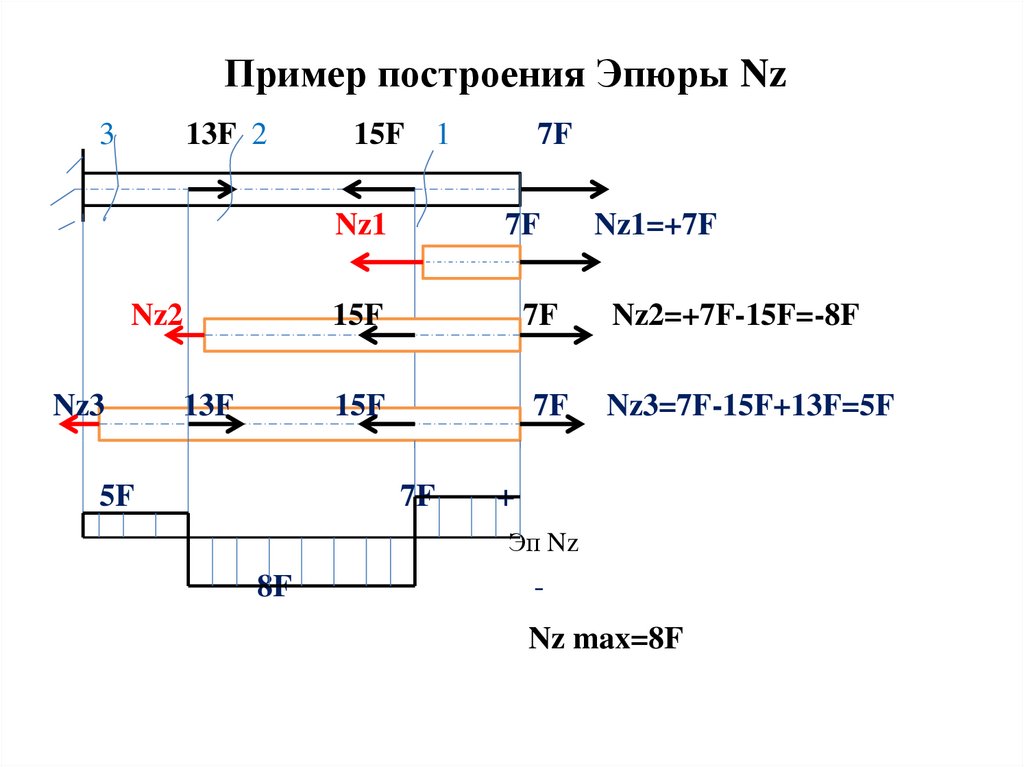
Пример построения Эпюры Nz
3
13F 2
Nz2
Nz3
13F
5F
15F
1
7F
Nz1
7F
Nz1=+7F
15F
7F
Nz2=+7F-15F=-8F
15F
7F
Nz3=7F-15F+13F=5F
7F
+
Эп Nz
8F
Nz max=8F

21.

Построение эпюр продольных сил
Nz
Построить эпюры Nz
F1=5н
F2=18н
F1=4н
F2=8н F3=22н
F3=20н

22.

Пример построения эпюр продольных усилий
и напряжений для ступенчатого бруса
Построить эпюры Nz и σ для бруса
2А
А
3А
Nz1=-5F
Nz2=-5F+8F=3F
20F
10F 8F 5F
Nz3=-5F+8F+10F=13F
4
3
2 1
Nz4= -5F+8F+10F-20F=-7F
13F 3F
+
σ1=Nz1/3А=-5F/3А =-5/3
Эп Nz
7F 6,5 13
5F -
3
3.5
6
4
3
2
σ3= Nz2/А=3F/А=3
Эп σ(F/А) σ4= Nz3/А=13F/А=13
5/3
σ5= Nz3/2А=13F/2А=6.5
1
5
σ2 =Nz2/3А=3F/3А =1
1
σ6= Nz4/2А=-7F/2А=-3.5

23.

Построить эпюры Nz и σ
F1=100 Кн F2=150 Кн F3=200 Кн А=0,1 м²
3 F3
F2 1
F1
4A
2A
A
Nz1=F1=100 Кн
150 2
100
Nz2=F1-F2=100-150=-50 Кн
Nz3=F1-F2+F3=100-150+200=150 Кн
Эп Nz (Кн)
50
5 4
3
375
125
250
2
500
1
1000
σ1=100:0,1= 1000 (КПа)
σ2=100:0,2= 500 (КПа)
σ3= -50:0,2= -250 (КПа)
σ4=--50:0,4= -125 (КПа)
σ5=150:0,4= 375 (КПа)
σmax=1000 КПа

24.

РАСТЯЖЕНИЕ – СЖАТИЕ
Продольные и поперечные деформации
Начальная длина бруса – Lo, начальная ширина сечения - а₀
Δa
Lo
ΔL
брус удлиняется на величинуΔL (при сжатии укорачивается)
ширина уменьшается на величину Δа (при сжатии увеличив.)
a
ΔL – абсолютное удлинение; Δa – абсолютное сужение
В сопротивлении материалов деформации рассчитывают
в относительных единицах
ε= ΔL /Lo – относительное удлиннение
ε’= Δ a/ а – относительное сужение

25.

Между продольной и поперечной деформацией есть
зависимость
ε‘= με, где μ- коэффициент поперечной деформации или
коэффициент Пуассона
Закон Гука
В пределах упругих деформаций нормальное напряжение
пропорционально относительному удлинению
σ = Еε
Е – модуль продольной упругости материала
(характеризует его жесткость)
Стр 341 табл. 5
Выписать чему равны модульно упругости и коэффициент Пуассона для
легированной стали

26.

Для расчета перемещений поперечных сечений бруса при
растяжении (сжатии) используют следующую формулу
NL
σL
ΔL=
=
AE
E
L – начальная длина бруса (мм)
E – модуль продольной упругости (Мпа)
N – продольная сила (Н)
А – площадь поперечного сечения (мм²)

27.

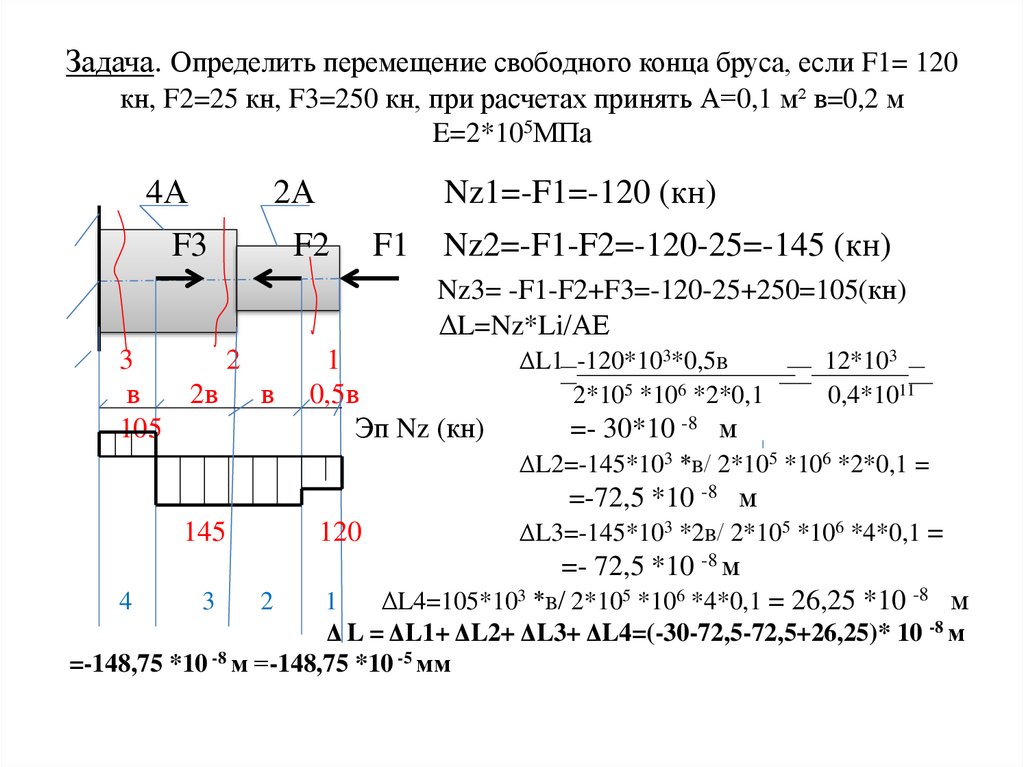
Задача. Определить перемещение свободного конца бруса, если F1= 120
кн, F2=25 кн, F3=250 кн, при расчетах принять А=0,1 м² в=0,2 м
E=2*105МПа
4А
2А
Nz1=-F1=-120 (кн)
F3
F2
F1
Nz2=-F1-F2=-120-25=-145 (кн)
Nz3= -F1-F2+F3=-120-25+250=105(кн)
ΔL=Nz*Li/АЕ
3
2
в
2в в
105
1
0,5в
Эп Nz (кн)
ΔL1 -120*103*0,5в
2*105 *106 *2*0,1
12*103
0,4*1011
=- 30*10 -8 м
ΔL2=-145*103 *в/ 2*105 *106 *2*0,1 =
=-72,5 *10 -8 м
145
120
ΔL3=-145*103 *2в/ 2*105 *106 *4*0,1 =
=- 72,5 *10 -8 м
1
ΔL4=105*103 *в/ 2*105 *106 *4*0,1 = 26,25 *10 -8 м
Δ L = ΔL1+ ΔL2+ ΔL3+ ΔL4=(-30-72,5-72,5+26,25)* 10 -8 м
=-148,75 *10 -8 м =-148,75 *10 -5 мм
4
3
2

28.

Механические испытания
Статические испытания на растяжение – сжатие
Схема испытаний (материал-пластичный)
нагрузка
d₀
Зарисовать схемы образцов
до и после испытаний рис. 22.2
F
L₀
ΔL
ΔL
F
F
4
5
σпц =F1 /A0-предел пропорциональности
Точка 2
до точки 2 материал может вернуться в исходное положение
3
2
1
Точка 1
до точки 1 удлинение растет пропорционально нагрузке
(выполняется закон Гука)
ΔL
σу = F2 /A0 -предел упругости
Точка 3
Удлинение растет без увеличения
нагрузки
Точка 4
Соответствует максимальной
нагрузке
σт предел текучести
σв предел прочности
Точка 5
Разрыв

29.

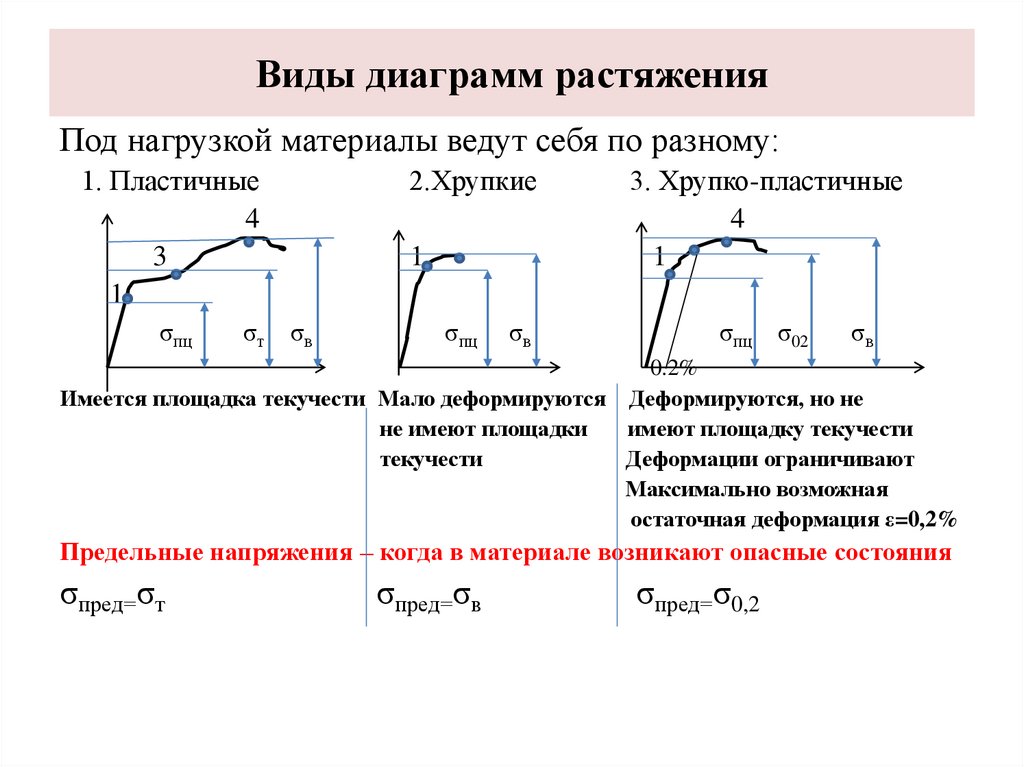
Виды диаграмм растяжения
Под нагрузкой материалы ведут себя по разному:
1. Пластичные
4
3
1
σпц
σт
2.Хрупкие
1
σв
σпц
σв
3. Хрупко-пластичные
4
1
σпц σ02
σв
0.2%
Имеется площадка текучести Мало деформируются Деформируются, но не
не имеют площадки
имеют площадку текучести
текучести
Деформации ограничивают
Максимально возможная
остаточная деформация ε=0,2%
Предельные напряжения – когда в материале возникают опасные состояния
σпред=σт
σпред=σв
σпред=σ0,2

30.

Допускаемые напряжения
Это максимальные напряжения при которых материал должен
нормально работать
[σ] – допускаемые напряжения
[σ]=σпред/[s]
[s] – допускаемый коэффициент запаса прочности
зависит от:
-качества материала;
-условий работы детали;
-назначения детали, точности обработки и расчета и т.д.
Пластичные материалы одинаково ведут себя при растяжении и сжатии
(механические характеристики одинаковы).
Хрупкие материалы обладают большей прочностью при сжатии чем при
растяжении. [σ]сж> [σ]р Расчет ведут отдельно на растяжение и сжатие.

31.

Расчеты на прочность при растяжении(сжатии
)
Условие прочности
σmax ≤ [σ], где σ=N /A
Три вида расчетов:
1. Проектный расчет
А≥ N max / [σ]
2. Проверочный расчет σ max =N max /A ≤ [σ]
3. Определение нагрузки [N]= [σ] *A
Таблица 6 стр. 342 учебника
Выбрать допускаемое напряжение [σ]р и [σ]сж для:
1. Стали легированной конструкционной
2. Чугун в отливках серый
Сделать вывод к какой группе материалов относится (1,2,3)

32.

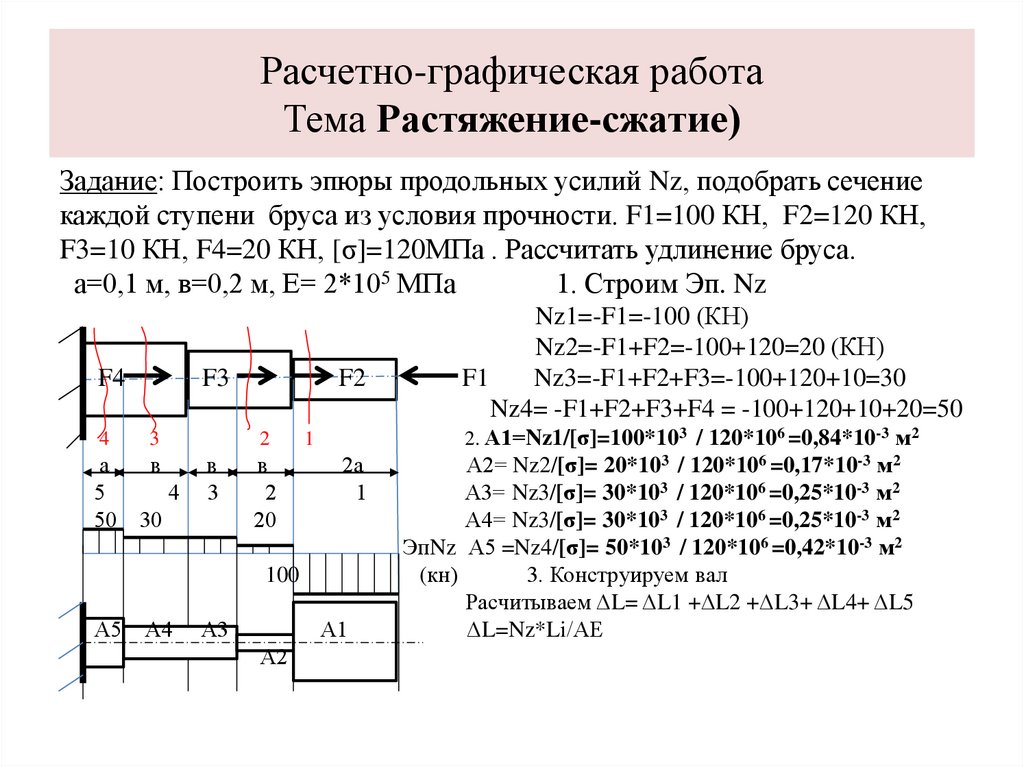
Расчетно-графическая работа
Тема Растяжение-сжатие)
Задание: Построить эпюры продольных усилий Nz, подобрать сечение
каждой ступени бруса из условия прочности. F1=100 КН, F2=120 КН,
F3=10 КН, F4=20 КН, [σ]=120МПа . Рассчитать удлинение бруса.
а=0,1 м, в=0,2 м, Е= 2*105 МПа
1. Строим Эп. Nz
F4
F3
4
3
а
5
50
в
F2
2
4
в
3
30
в
2
20
2. А1=Nz1/[σ]=100*103 / 120*106 =0,84*10-3 м2
1
2а
1
100
А5
А4
А3
А1
А2
Nz1=-F1=-100 (КН)
Nz2=-F1+F2=-100+120=20 (КН)
F1
Nz3=-F1+F2+F3=-100+120+10=30
Nz4= -F1+F2+F3+F4 = -100+120+10+20=50
А2= Nz2/[σ]= 20*103 / 120*106 =0,17*10-3 м2
А3= Nz3/[σ]= 30*103 / 120*106 =0,25*10-3 м2
А4= Nz3/[σ]= 30*103 / 120*106 =0,25*10-3 м2
ЭпNz А5 =Nz4/[σ]= 50*103 / 120*106 =0,42*10-3 м2
(кн)
3. Конструируем вал
Расчитываем ΔL= ΔL1 +ΔL2 +ΔL3+ ΔL4+ ΔL5
ΔL=Nz*Li/АЕ

33.

ΔL=Nz*Li/АЕ
ΔL1=Nz1*2а/А1Е=-100*103 *2*0,1/0,84*10-3 *2*105 *106=-11,91*10-5 м
ΔL2=Nz2*в/А2Е=20*103 *0,2/0,17*10-3 *2*105 *106=11,76*10-5 м
ΔL3=Nz3*в/А3Е=30*103 *0,2/0,25*10-3 *2*105 *106=12*10-5 м
ΔL4=Nz3*в/А4Е= 30*103 *0,2/0,25*10-3 *2*105 *106=12*10-5 м
ΔL5=Nz4*а/А5Е= 50*103 *0,1/0,42*10-3 *2*105 *106=5,95*10-5 м
ΔL=10-5 (-11,91+11,76+12+12+5,95)=29,8*10-5 м

34.

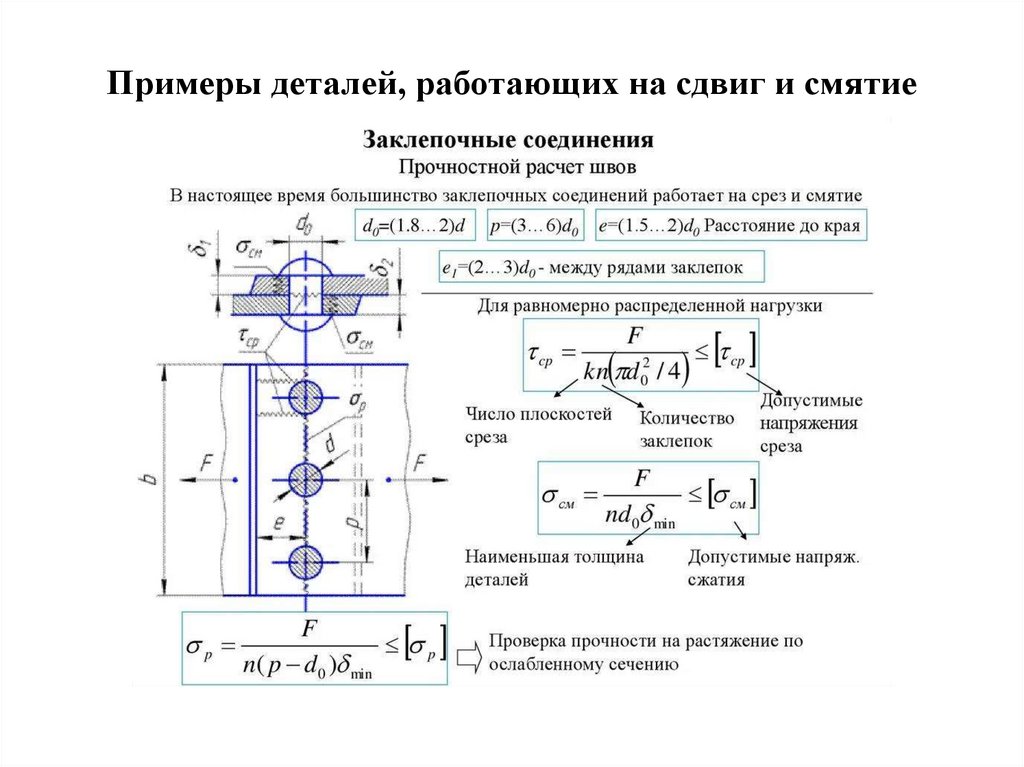
Практические расчеты на срез и смятие
Детали соединений: болтом, штифтом, шпонкой, заклепкой
рассчитывают на сдвиг (срез) и смятие
Сдвиг – нагружение, при котором в поперечном сечении
бруса возникает только один внутренний силовой фактор –
Q - поперечная сила.
F
y
o
b
F
F
∑ Fy=F- Q=0 F=Q
Рассмотрим напряженное состояние в точке b
Q

35.

Выделим элемент в виде бесконечно малого
параллелепипеда, к граням которого приложены напряжения
τ
τ
Напряженное состояние
Δ
γ
Деформированное состояние
Δ – абсолютный сдвиг
γ – угол сдвига
Закон парности касательных напряжений.
Закон Гука при сдвиге τ=G*γ
G – модуль упругости сдвига =0,4Е (Мпа)

36.

Расчет на сдвиг носит условный характер
Допущения:
- При расчете на сдвиг изгиб детали не учитывается;
- Считаем, что силы упругости распределены по сечению
равномерно;
- Если для передачи используют несколько деталей, то
считаем, что внешняя сила распределена между ними
равномерно.
Напряжение τс=Q/Ас
Q=F/ Z
τ с- касательное напряжение
Ас площадь сдвига
Q -поперечная сила F -внешняя сдвигающая сила
Z – количество деталей

37.

Условие прочности при сдвиге
τс=Q/Ac≤[τc]
[τc] – допускаемое напряжение сдвига
[τc]=(0,25-0,35)σт
Часто вместе со сдвигом происходит смятие боковой
поверхности в месте контакта в результате передачи нагрузки
с одной поверхности на другую. При этом возникают
сжимающие напряжения – смятия – σсм
Расчет носит условный характер, допущения такие же как и
при сдвиге, но при расчете боковой цилиндрической
поверхности напряжения распределены не равномерно,
поэтому расчет ведут для наиболее нагруженной точке.

38.

Условие прочности при смятии
σсм=F/Асм≤[σсм]
Асм=dδ, расчетная площадь смятия, где
d -диаметр окружности сечения
δ – наименьшая высота соединяемых пластин
F – сила взаимодействия, [σсм]=(0,35-0,4)σт
δ
F
F
σсм
В
F

39.

Примеры деталей, работающих на сдвиг и смятие

40.

Расчетно-графическая работа
Расчет заклепочного соединения
• Определить требуемое количество заклепок для передачи силы
F. Заклепки расположить в ряд, проверить прочность на смятие,
проверить прочность соединяемых листов на растяжение.
• Допускаемое напряжение на растяжение - [σ]
• Допускаемое напряжение на срез (сдвиг) [τс]
• Допускаемое напряжение на смятие [σсм]
• d – диаметр заклепок, δ1 и δ2 – толщина соединяемых пластин
• 1. Из условие среза определяем количество заклепок
n=4F/ k do
2. Проверяем прочность на смятие
F/nd0 min см

41.

Заклепочное соединение
3. Проверить прочность соединяемых листов на
растяжение
Расчет по ослабленному сечению
F/n(p-d0 ) min p
4. Вычертить схему полученного соединения

42.

Кручение
Кручение происходит под действием скручивающих
моментов
Образующая поворачивается на угол γ угол сдвига.
Поперечное сечение разворачивается
на угол φ – угол закручивания
угол φ
1 γ
2’
М
2
R
z
Кручением называется нагружение, при котором в поперечном
сечении бруса возникает один силовой фактор – крутящий момент
Мz (Нм)
Изменение крутящего момента по длине бруса определяется при
построении эпюры крутящих моментов. При построении используют
метод сечения

43.

Крутящий момент в сечении равен сумме моментов
внешних сил, действующих на отсеченную часть
Правило знаков
Мz=∑Mi
Отс.
Если известна мощность (Р)
и угловая скорость (ω), то
_
+
М=Р/ ω, где Р (Вт или КВт)
ω (рад/с).
При кручении в поперечном сечении возникают касательные
напряжения – τ к (Па)
τк
Распределение касательных
напряжений по сечению

44.

τ=Мz/Wρ
Где М z - крутящий момент
Wρ - полярный момент сопротивления сечения
Wρ =Jρ/ρ для круглого сечения Wρ=0,2d3
Условие прочности при кручении
τmax=Mzmax /Wρ ≤[τ]
1. Проектный расчет
Определяем диаметр бруса в опасном сечении
τmax=Mzmax /0,2d3 ≤[τ] откуда
d≥3√Мz/0.2[τ]

45.

2 Проверочный расчет
τmax=Mzmax /Wρ ≤[τ]
3. Определение нагрузочной способности
[M]= [τ] Wρ
Жесткость сечения при кручении
Закон Гука при кручении τ= G* γ
Характеристика жесткости материала при кручении
G – модуль упругости при сдвиге (МПа) (стр. 341 табл. 5)
Деформация – угол закручивания
φ= МzL/GJρ
Условие жесткости при кручении
φо= Мz/GJρ≤ [φо]

46.

Расчетно-графическая работа №__
Тема: Кручение
Определить крутящие моменты на валу. Определить из условия прочности и
жесткости диаметр вала постоянного по длине, если
=60 МПа, о =0.4 град/м, G=8 10 10Па.(Р1=200, Р2=300, Р3=150 (Квт)
Вал вращается с постоянной угловой скоростью =2 рад/с
Р1
Р2
Р3
Р4
1. Определяем моменты
М1
М2 М3
М4
М1=Р1/ω= 200/2=100 (кнм)
5
4
3
2
1
М2=Р2/ ω=300/2=150 (кнм)
М3=Р3/ ω=150/2=75 (кнм)
М1-М2-М3…..М4=0
а 2а
3а
2а
2а
100-150-75+125=0
М4= 125 (Кнм)
125
2. Строим Эпюру Мz
50
Мz1 =0 Мz2 =M4=125 (кнм)
Эп Мz Мz3= М4-М3=125-75=50 (кнм)
100
( Кнм) Мz4= М4-М3-М2=125-75-150=
-100 (кнм)

47.

3. Определяем диаметр вала из условия прочности
МZ max=125 кн
d проч=3√Мz/0,2 [τ] = 3√125*103/0,2* 60*106
= 2.19*10-1 (м)=220 мм
4. Определяем диаметр вала из условия жесткости
d жест=4√Мz/0,1* [φo] *G = 4√125*103/0,1* 0,008* 8 10 10 = 2,1*10-1 (м)
[φo] =0.008 рад/м
Принимаем d проч=220 мм

48.

Таблица
Вид нагружения (схема)
Внутренний силовой фактор (обозначение
наименование, единица измерения)
Напряжение (обозначение наименование, единица
измерения)
Условие прочности
Деформации (обозначение, наименование, ед.изм.)
Геометрические характеристики сечения,
используемые при расчете на прочность и
жесткость (обозначение, наименование, ед. изм.)
Характеристика жесткости материала (обозначение,
наименование, ед. изм.)

49.

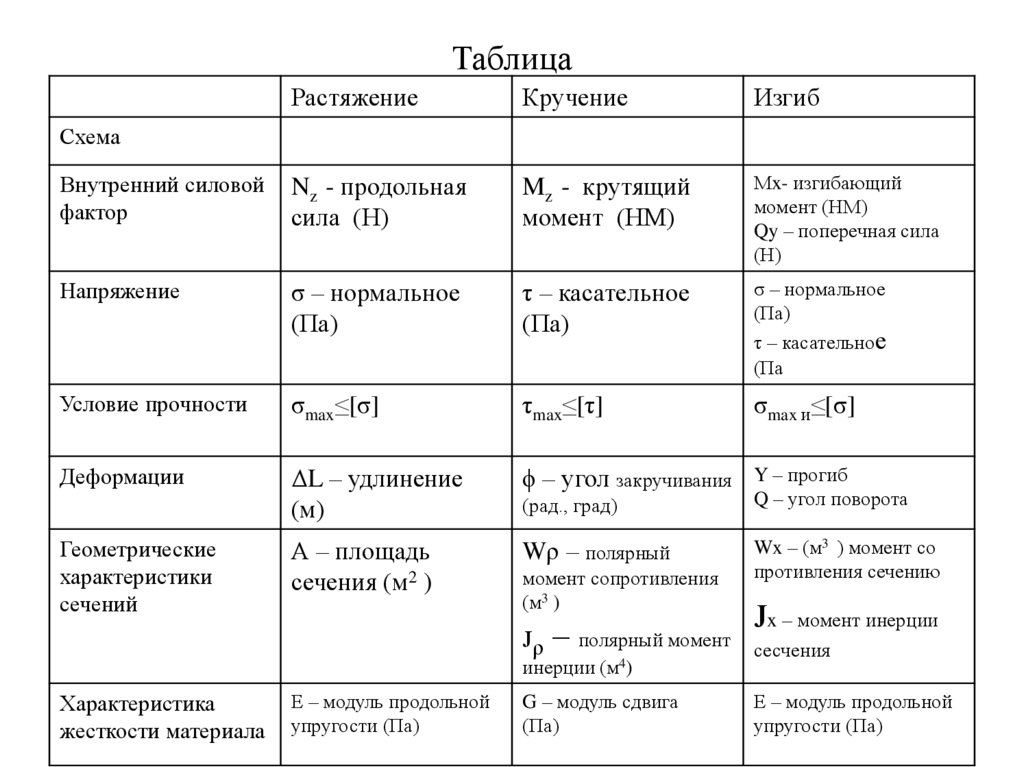
Таблица
Растяжение
Кручение
Изгиб
Внутренний силовой
фактор
Nz - продольная
сила (Н)
Mz - крутящий
момент (НМ)
Мx- изгибающий
момент (НМ)
Qy – поперечная сила
(Н)
Напряжение
σ – нормальное
(Па)
τ – касательное
(Па)
σ – нормальное
(Па)
τ – касательное
(Па
Условие прочности
σmax≤[σ]
τmax≤[τ]
σmax и≤[σ]
Деформации
ΔL – удлинение
(м)
ϕ – угол закручивания
Y – прогиб
Q – угол поворота
А – площадь
сечения (м2 )
Wρ – полярный
Схема
Геометрические
характеристики
сечений
(рад., град)
момент сопротивления
(м3 )
Wx – (м3 ) момент со
противления сечению
ᴊx – момент инерции
ᴊρ – полярный момент сесчения
инерции (м4)
Характеристика
жесткости материала
Е – модуль продольной
упругости (Па)
G – модуль сдвига
(Па)
Е – модуль продольной
упругости (Па)

50.

Изгиб
Изгиб бывает:
1.Чистый изгиб - называется вид деформации, при котором
в поперечном сечении бруса возникает один внутренний
силовой фактор – изгибающий момент Мx
2. Поперечный изгиб - называется вид деформации, при
котором в поперечном сечении бруса возникают два
внутренних силовых фактора: изгибающий момент Мx и
поперечная сила Qy.
Плоскость в которой расположены внешние силы и моменты
называется – силовой плоскостью.

51.

Если все силы лежат в одной плоскости изгиб называется
плоским
Плоскость проходящая через продольную ось бруса и одну
из главных центральных осей его поперечного сечения
называется главной плоскостью бруса.
F
Ось
бруса
M
Силовая плоскость

52.

Если силовая плоскость совпадает с главной плоскостью
бруса изгиб называется прямым
Если силовая плоскость не совпадает с главной
плоскостью изгиб называется косым
Изгибающий момент в произвольном поперечном
сечении бруса численно равен алгебраической сумме
моментов всех внешних сил, приложенных к отсеченной
части, относительно рассматриваемого сечения
Mx=∑Mсеч(Fi)
Поперечная сила в произвольном поперечном сечении
бруса численно равна алгебраической сумме проекций
всех внешних сил, действующих на отсеченной части на
ось
Qy=∑Fi

53.

Графики показывающие изменение изгибающего момента
и поперечной силы по длине бруса (балки) называется
эпюрой Мx и эпюрой Qy
При построении используют метод сечения

54.

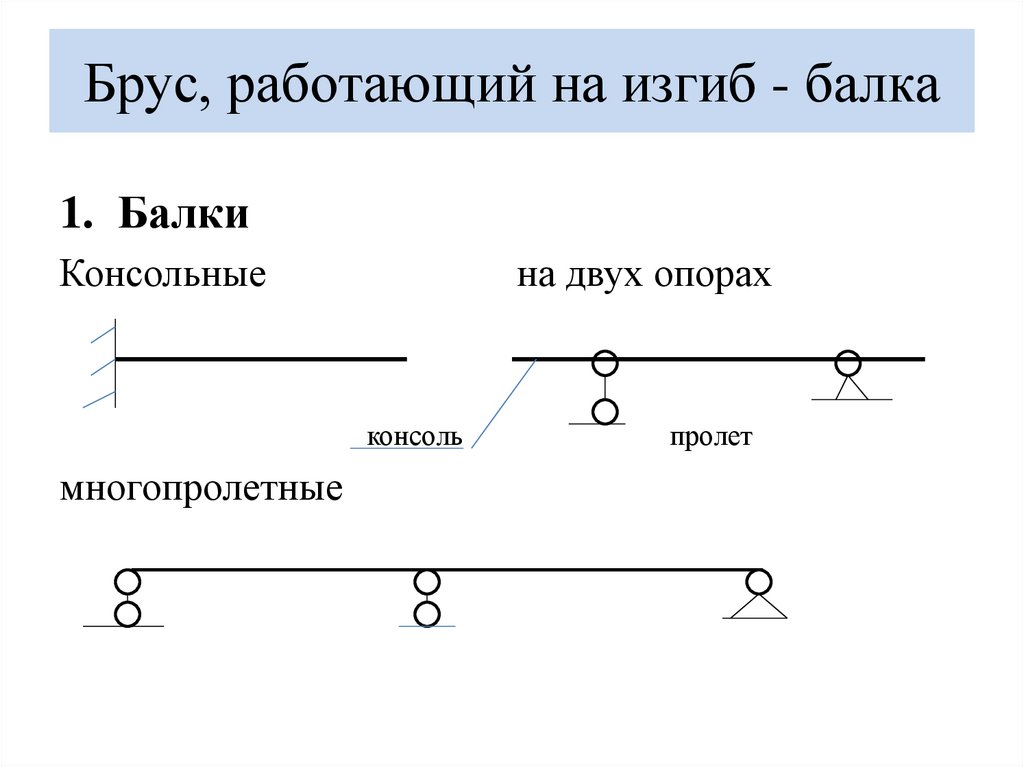
Брус, работающий на изгиб - балка
1. Балки
Консольные
на двух опорах
консоль
многопролетные
пролет

55.

Правила знаков для изгибающего момента
Рассматриваем левую
F
M
Mx
Mx
Рассматриваем правую
Mx
M
F
Если внешняя сила стремится
повернуть, отсеченную часть
по часовой стрелке
F M
Если внешняя сила стремится
повернуть, отсеченную часть
если против часовой стрелке
M
F
Mx
если против часовой стрелке
Mx
по часовой стрелке

56.

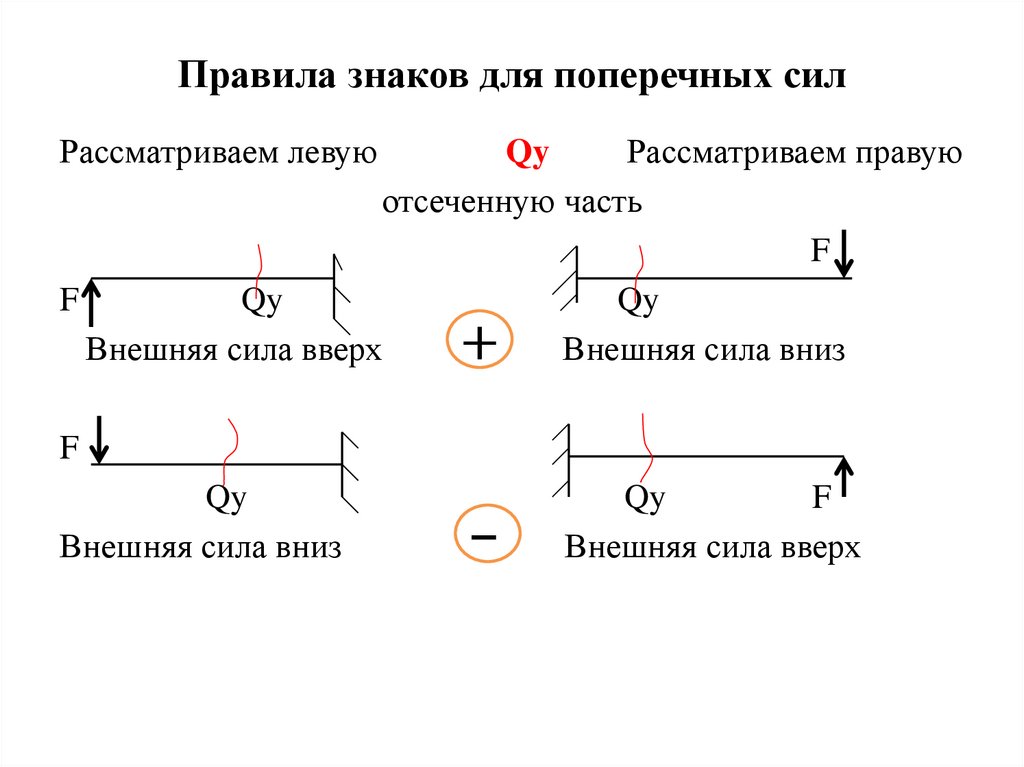
Правила знаков для поперечных сил
Рассматриваем левую
Qy
Рассматриваем правую
отсеченную часть
F
F
Qy
Qy
Внешняя сила вверх
Внешняя сила вниз
F
Qy
Внешняя сила вниз
Qy
F
Внешняя сила вверх

57.

Условие прочности при изгибе
При чистом изгибе в поперечном сечении возникает
1 силовой фактор – Ми (Мx)
нейтральный слой (нормальные напряжения σ=0)
растянуты
сжаты
Нормальные напряжения равны
σ=Ми/WX,
Ми – изгибающий момент
WX, - момент сопротивления сечению при изгибе или
осевой момент сопротивления (м3), (характеризует влияние
формы и размеров сечения на прочность при изгибе)

58.

Рациональные сечения при изгибе
σр Для балок из пластичных материалов
в
в
в
в
y1
y2
σс
Сечения не рациональныe
Рациональное
Для балок из хрупких материалов (большей прочностью на сжатие)
σр
Для определения напряжения в точке В
σс
σв=Мx*y1/Jx

59.

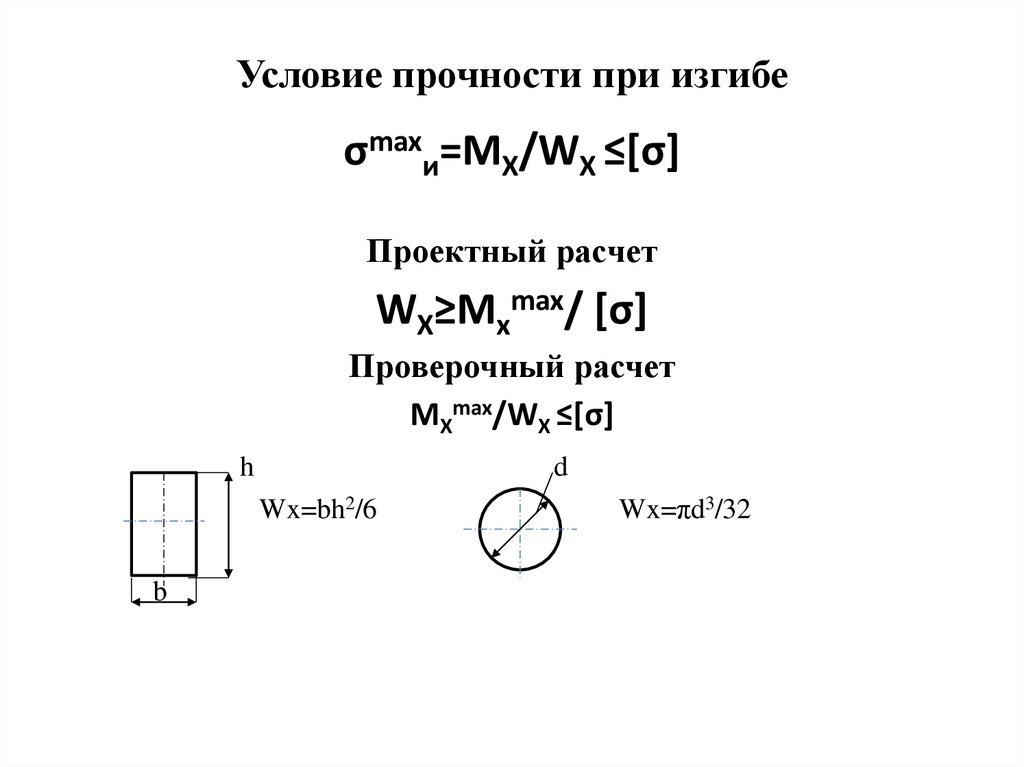
Условие прочности при изгибе
σmaxи=МX/WX ≤[σ]
Проектный расчет
WX≥Мxmax/ [σ]
Проверочный расчет
МXmax/WX ≤[σ]
h
d
Wx=bh2/6
b
Wx=πd3/32

60.

Понятие о касательных напряжениях при
изгибе, перемещения при изгибе
Поперечная сила Qy - представляет собой
равнодействующую касательных сил в поперечных сечениях,
а значит вызывает в поперечном сечении касательные
напряжения.
На поверхности сечения касательные напряжения равны
нулю.
Формула для расчета касательных напряжений для балки
квадратного сечения (1855 г. русский инженер Д.И. Журавский)
τ= Qy*Sx /Jx*b
b - ширина балки; Sx- статический момент отсеченной части.

61.

Наибольшие касательные напряжения достигаются
на нейтральной оси
τmax=1,5Qy/A (А – площадь сечения)
σи max
σи max
τmax
τmax
Для длинных балок расчет проводится по нормальным
напряжениям
Для коротких балок, нагруженных значительными
поперечными силами вблизи опор проводят расчет по
касательным напряжениям.

62.

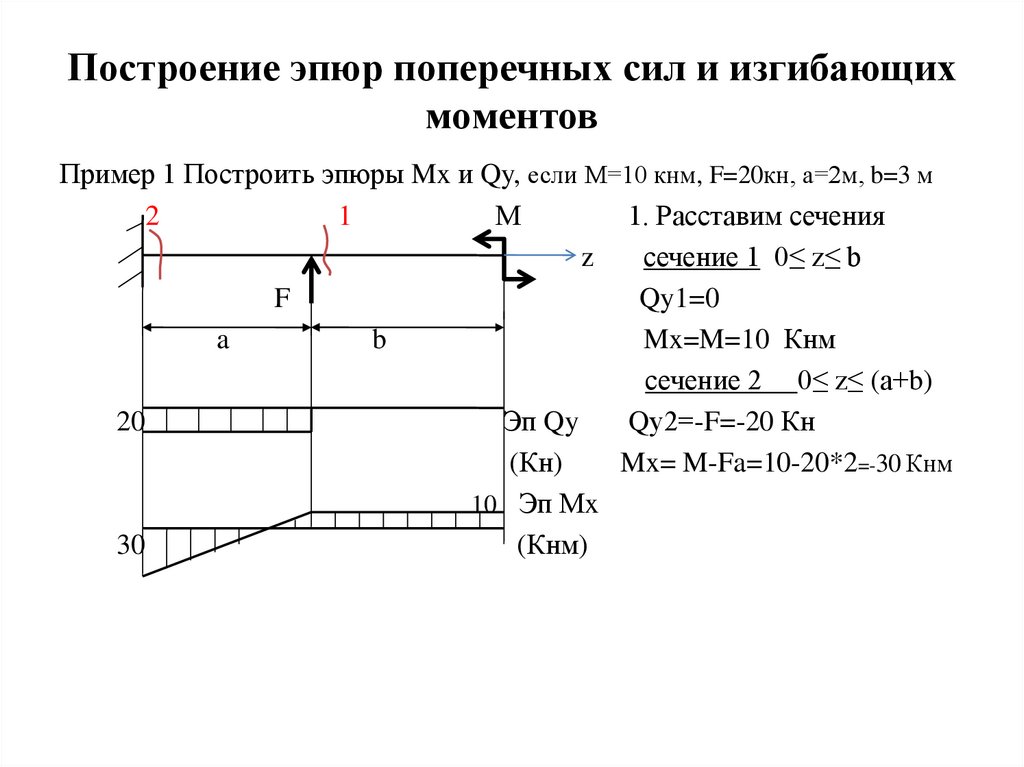
Построение эпюр поперечных сил и изгибающих
моментов
Пример 1 Построить эпюры Mx и Qy, если М=10 кнм, F=20кн, а=2м, b=3 м
2
1
М
1. Расставим сечения
z
сечение 1 0≤ z≤ b
F
Qy1=0
a
b
Mx=M=10 Кнм
сечение 2 0≤ z≤ (а+b)
20
Эп Qy
Qу2=-F=-20 Кн
(Кн)
Mx= M-Fa=10-20*2=-30 Кнм
10 Эп Мx
30
(Кнм)

63.

Пример 2 Построить эпюры Mx и Qy, если F1=10 кн, F2=20кн,
а=2м, b=3 м
Решение
2
z2
a
F1
1
z1
F2 z
b
-
10
20
80
+
60
Сечение 1 0 ≤ z1≤ b
Qy1=- F2 =-20
Mx1=F2*z
при z=0 Mx1=0
при z=b Mx1=F2*b=20*3=60
Сечение 2 0≤z2≤a
Qy2=- F2+F1=-20+10=-10
My2=F2*(z+b)-F1*z
при z=0 Mx2=F2*b=20*3=60
при z=a Mx2=F2(a+b)-F1*a=
20*(2+3)-10*2=80

64.

Построить эпюры изгибающих моментов и поперечных сил
Если F=10 н, M=5 нм, q=4н/м
F
q
M
4
3
a
2
1
a
14
4
+
10
-
1
Эп Mx (Нм)
Qy1=0
Qy2=q*a=4*1=4н
Qy3пр=q*a=4*1=4 н
a
3
a=1 м
1. Строим Эпюру Qy
+
Qy3л=q*a+F=4*1+10=14 н
Qy4=q*a+F=4*1+10=14 н
Эп Qy 2. Строим эпюру Mx
(н)
Mx1=M=5
5
Mx2=M-q*a*a/2=5-4*1*0.5=3
Mx21=M-q*a/2*a/4=5-1*0.5*0,25=4,875
Мx3= M-q*a*(a+a/2)=5-4*1*1.5=-1
Mx4=M-q*a*(2a+a|2)=5-4*1*2.5=-10

65.

Порядок проектного расчета балок на двух опорах
1. Обозначим опоры и нанесем реакции
2. Определяем реакции опор
3. Делаем проверку
4. Строим эпюры поперечных сил и изгибающих
моментов
5. Определяем максимальный изгибающий момент
6. Определяем размеры поперечного сечения из
условия прочности
7. Определяем прогиб в середине балки

66.

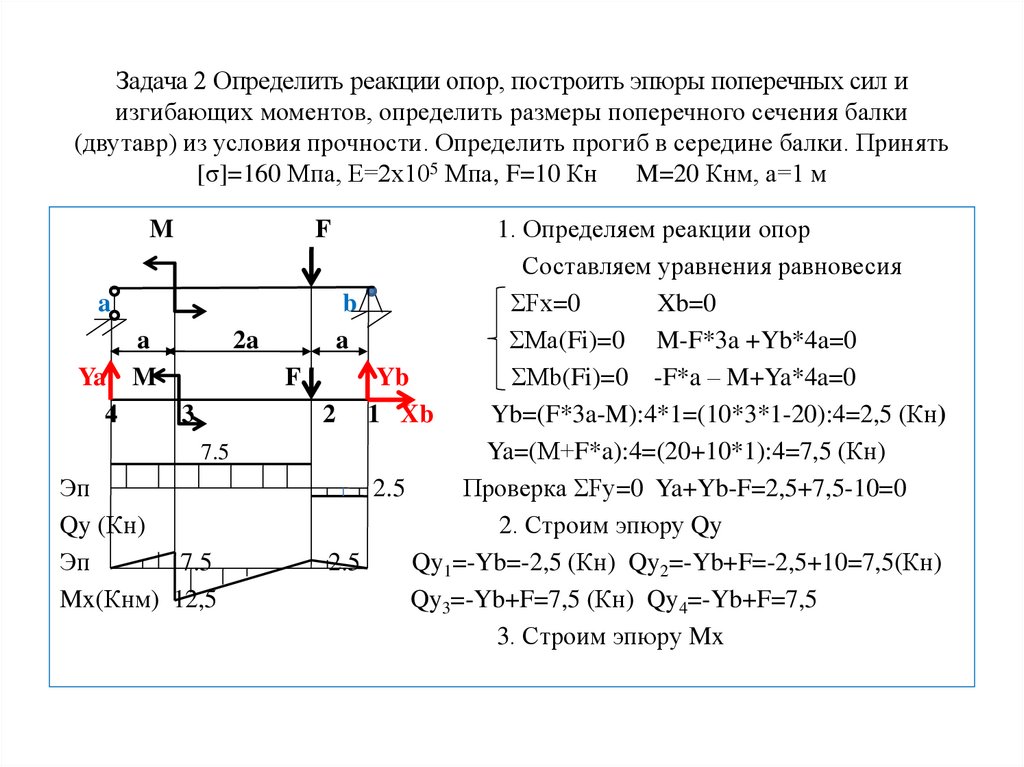
Задача 2 Определить реакции опор, построить эпюры поперечных сил и
изгибающих моментов, определить размеры поперечного сечения балки
(двутавр) из условия прочности. Определить прогиб в середине балки. Принять
[σ]=160 Мпа, Е=2х105 Мпа, F=10 Кн
M=20 Кнм, а=1 м
M
a
Ya
4
1. Определяем реакции опор
Составляем уравнения равновесия
b
ƩFx=0
Xb=0
a
ƩMa(Fi)=0 M-F*3a +Yb*4a=0
F
Yb
ƩMb(Fi)=0 -F*a – M+Ya*4a=0
2 1 Xb
Yb=(F*3a-M):4*1=(10*3*1-20):4=2,5 (Кн)
Ya=(М+F*a):4=(20+10*1):4=7,5 (Кн)
2.5
Проверка ƩFy=0 Ya+Yb-F=2,5+7,5-10=0
2. Строим эпюру Qy
2.5
Qy1=-Yb=-2,5 (Кн) Qy2=-Yb+F=-2,5+10=7,5(Кн)
Qy3=-Yb+F=7,5 (Кн) Qy4=-Yb+F=7,5
3. Строим эпюру Mx
F
a
M
2a
3
7.5
Эп
Qy (Кн)
Эп
7.5
Mx(Кнм) 12,5

67.

Мx1=0
Mx2=Yb*a=2,5*1=2,5 (Кнм)
Mx3до=Yb*3a-F*2a=2,5*3*1-10*2*1=-12,5 (Кнм)
Mx3 после= Yb*3a-F*2a+M=2,5*3*1-10*2*1+20=7,5 (Кнм)
Mx4= M-F*3a +Yb*4a=20-10*3+2,5*4=0
Mxmax=12,5 Кнм
3. Определяем размеры поперечного сечения балки из условия прочности
Wx=Mxmax /[σ]=12,5*103/160*106 =0,079*10-3 м3 = 0,079*10-3 106=79 см3
Из таблицы сортамента выбираем двутавр №14 Wx=81,7 см3
4. Определяем прогиб в середине балки.
4.1 Прикладываем в середине пролета силу F=1
Определяем реакции опор от единичной силы
ƩFx=0
Xb=0
ƩMa(Fi)=0 -F*2a+Yb*4a=0
Yb=F*2a : 4a=1*2*1:4=0,5
ƩMb(Fi)=0 -F*2a + Ya*4a=0
Ya=F*2a : 4a= 1*2*1:4=0,5
4.2 Строим эпюру изгибающих моментов от действия силы F=1 и реакций

68.

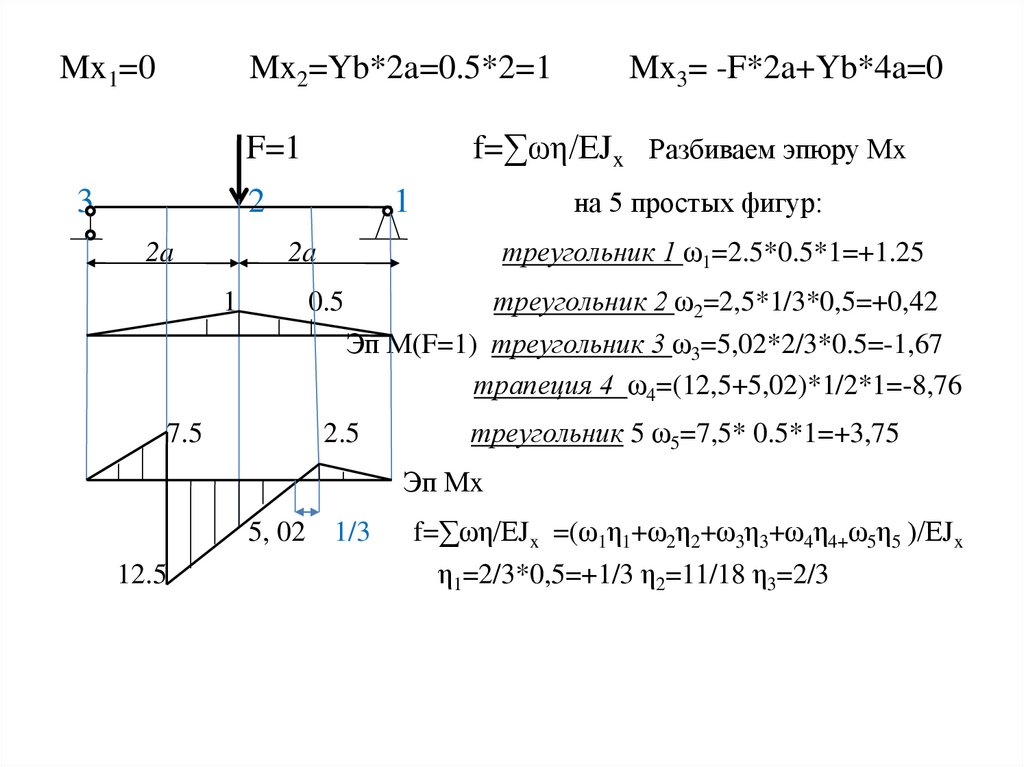
Mx1=0
Mx2=Yb*2a=0.5*2=1
f=∑ωη/ЕJx Разбиваем эпюру Мx
F=1
3
2
2a
7.5
на 5 простых фигур:
1
треугольник 1 ω1=2.5*0.5*1=+1.25
2a
1
Mx3= -F*2a+Yb*4a=0
0.5
треугольник 2 ω2=2,5*1/3*0,5=+0,42
Эп М(F=1) треугольник 3 ω3=5,02*2/3*0.5=-1,67
трапеция 4 ω4=(12,5+5,02)*1/2*1=-8,76
2.5
треугольник 5 ω5=7,5* 0.5*1=+3,75
Эп Мx
5, 02 1/3
12.5
f=∑ωη/ЕJx =(ω1η1+ω2η2+ω3η3+ω4η4+ω5η5 )/ЕJx
η1=2/3*0,5=+1/3 η2=11/18 η3=2/3

69.

Пример определения η
1 η3
η2 0,5 η1
0,5: η1=а:2/3а η1=0,5*2/3=1/3
2/3а
а+ 1/3а*1/3
2,5
x=1/3*а
5.02
2а- 1/3*2/3а
Ц.Т.1
5,02: 2.5=(а- x): x
5,02 x=2,5(а- x)
x=1/3а
1: η2=2а:(а+1/9а) η2=10/9:2=5/9
1: η3=2а:(2а-1/3*2/3а)
η3=16/9:2=8/9

70.

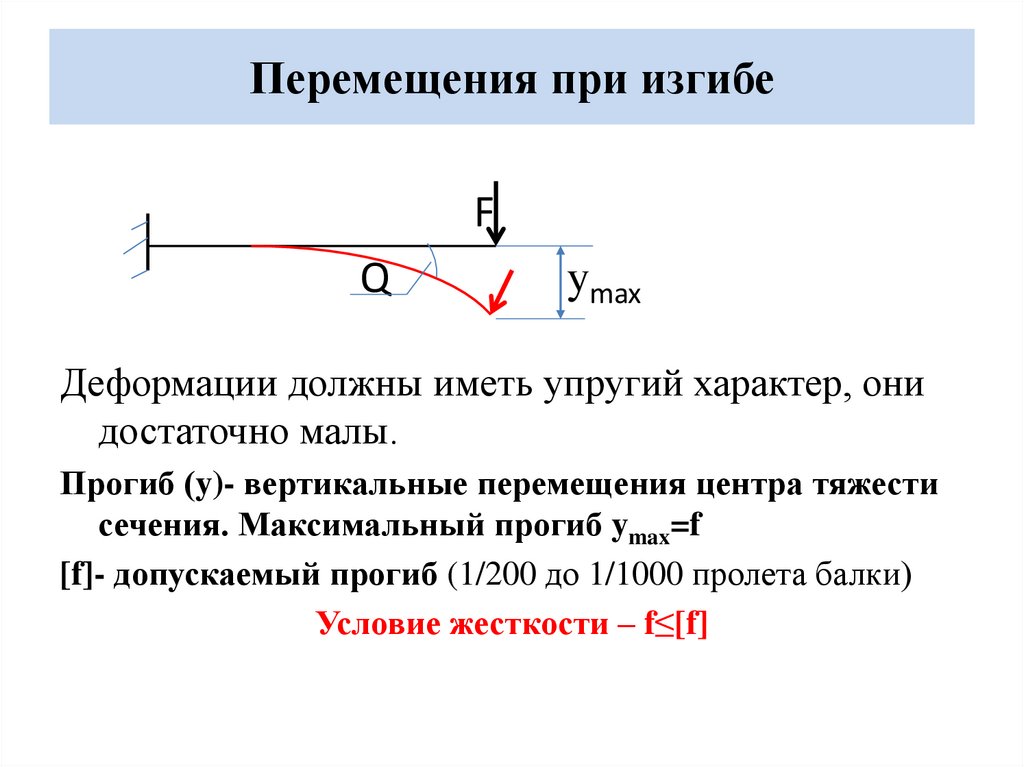
Перемещения при изгибе
F
Q
ymax
Деформации должны иметь упругий характер, они
достаточно малы.
Прогиб (y)- вертикальные перемещения центра тяжести
сечения. Максимальный прогиб ymax=f
[f]- допускаемый прогиб (1/200 до 1/1000 пролета балки)
Условие жесткости – f≤[f]

71.

Иногда проверяется угол поворота сечения - Q
Q ≤ [Q] (1*10-3 рад)
Методы определения перемещений:
1. Дифференцирование упругой линии
2. Метод Мора
3. Для простейших случаев нагружения
используют таблицы (табл. 33.1 стр. 274-275)

72.

Табличный способ (3)
F
3а
а
f F=F*3a *[3(4a)2-4(3a)2]/48EJx
fF
4а
q
2a
fq
fq=5q(4a)4/768EJx
4a
Общий прогиб в середине балки f=fF+fq

73.

Определение прогиба при помощи интеграла
Мора по правилу Верещагина
Перемещение произвольного сечения балки
f=∑ Mxf*M1dz/EJx = ∑ωη/ЕJx
Mxf – изгибающий момент (эпюра моментов от внешней нагрузки)
M1 – момент от единичной силы
Правило Верещегина
Каждое из слагаемых, входящих в интеграл Мора, равно
произведению площади ω нелинейной эпюры изгибающих
моментов на ординату η линейной эпюры под центром тяжести
нелинейной, деленной на жесткость сечения данного участка

74.

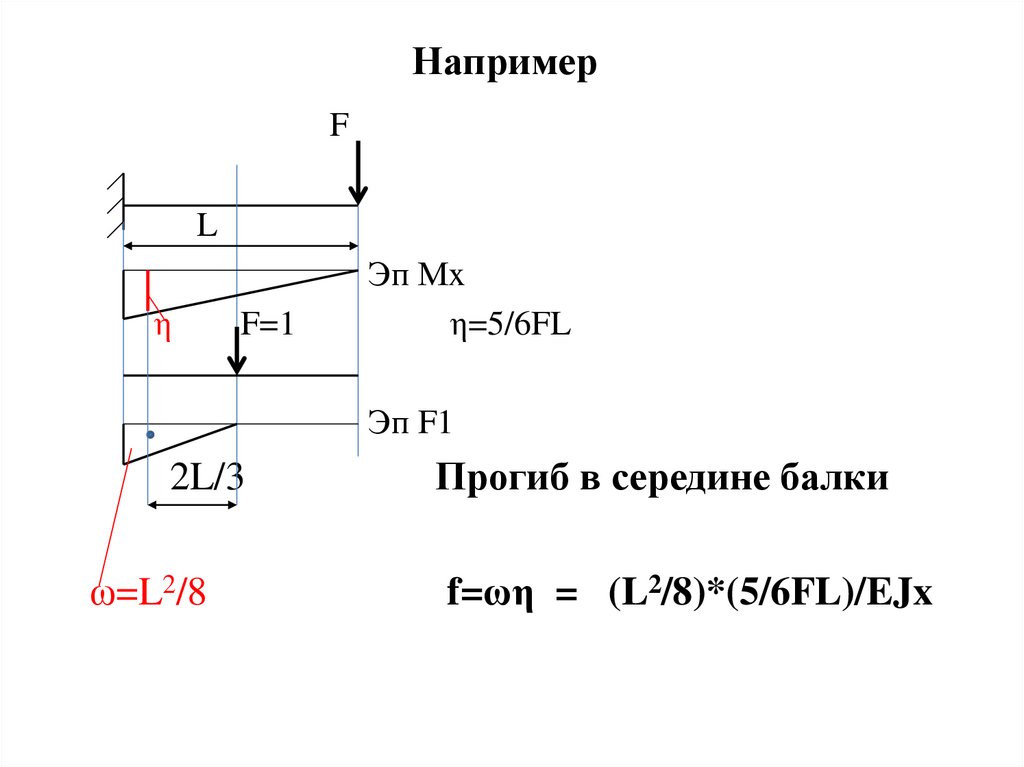
Например
F
L
η
F=1
Эп Мx
η=5/6FL
Эп F1
2L/3
ω=L2/8
Прогиб в середине балки
f=ωη = (L2/8)*(5/6FL)/EJx

75.

Общие указания
1. Всю эпюру, если она сложная необходимо разбить на
участки.
2. Произведение площади нелинейных эпюр на ординату
линейной эпюры считается положительным, если
площадь и ордината по одну сторону от оси балки.
3. Если обе эпюры линейны, то безразлично площадь какой
брать.
4. Единичную силу необходимо приложить в том месте, где
необходимо найти прогиб

76.

Сочетание основных деформаций.
Гипотезы прочности
Напряженное состояние в точке характеризуется
нормальными и касательными напряжениями.
Обычно достаточно определить напряжения на трех взаимно
перпендикулярных площадках.
Среди множества площадок, которые можно провести через
точку, есть три такие взаимно перпендикулярные площадки
на которых касательные напряжения равны 0 – главные
площадки.
Нормальные напряжения на этих площадках
называются главными: σ1 σ2 σ3
σ1-максимальное
σ3-минимальное

77.

Классификация видов напряженного состояния
1. Объемное (трехосное)
σ2
σ1
σ1
σ3
σ2
Все три главных напряжения
не равны «0»
3. Линейное
σ1
2. Плоское (двухосное)
σ1
σ1
σ2
Одно из главных равно «0»
σ1
Если одно из главных
не рано «0»

78.

Понятие о сложном деформированном состоянии
Сложное деформированное состояние возникает, если деталь
одновременно подвергается нескольким простейшим
нагружениям.
Для упрощения расчетов применяют теории прочности.
(замена реального сложного деформированного состояния
равноопасным)ю
Сравнение равноопасных состояний производится с
помощью эквивалентного (простого) напряженного
состояния. Обычно заменяют простым растяжением.
Полученное расчетным путем эквивалентное напряжение для
точки сравнивается с предельным.
Условие прочности σэкв≤[σ]

79.

Предельные напряженные состояния у пластичных
материалов наступает в результате пластических
деформаций, а у хрупких в результате разрушения.
Для пластичных материалов используют:
Гипотезу максимальных касательных напряжений: два
напряженных состояния равноопасны, если максимальные
касательные напряжения у них одинаковы (3-я гипотеза)
- Гипотеза потенциальной энергии формообразования: два
напряженных состояния равнопасны, если энергия формоизменения у
них одинакова (5-я гипотеза)
Для хрупких и хрупкопластичных материалов применяют теорию
прочности Мора.
σэквIII=√σ2+4τ2
-
σэкв v=√σ2+3τ2
σи=Mи/Wx
τк= Mк/Wρ
σр=Nz/А

80.

σ= Nz/А+Mи/Wx
Проверить прочность бруса круглого поперечного сечения,
принять [σ]=120 Мпа
F2
a
F1
a
M
F1
Эп Nz
Эп Ми
F2*a
Эп Мк
M
Считаем σэквIII=√σ2+4τ2
σэкв v=√σ2+3τ2
если σэкв≤[σ]
Опасное сечение в заделке
σр=Nz/A=F1/А А=πd2/4
σ и=Mи/Wx
Wx=0.1 d3
σ=σи +σр
τ=Мк/Wρ
Wρ=0,2d3
или
и проверяем:
условие прочности соблюдается, если нет увеличить диаметр

81.

Сопротивление усталости
Разрушения
деталей
вследствие
возникновения
переменных напряжений – усталостные
Под влиянием переменных напряжений металл «устает»
и из пластичного переходит в хрупкий.
Процесс разрушения начинается
с появления
микротрещин, которые увеличиваются со временем.
Усталость
–
процесс
постепенного
накопления
напряжений, приводящих к изменению свойств,
образованию трещин, их развит.ию и разрушению

82.

Рассмотрим возникновение переменных напряжений на
примере работы вращающейся оси, нагруженными силами.
F1
F
σи
k3
k2
k1
F
ω
F1
σр
k0,k4
За один оборот точка попеременно
попадает из зоны растяжения
в зону сжатия.
К1 – максимальные растяжения
К2,0,4 – напряжения равны нулю
К3 – максимальные сжатия
Если приложить силу F1 – растягивающую, то в любой момент времени
напряжение в точке К можно вычислить по формуле
σк=F1/А +σmax*sinωt
В этом случае график изменения напряжения будет синусоидальным, но
сама синусоида сместиться вверх.

83.

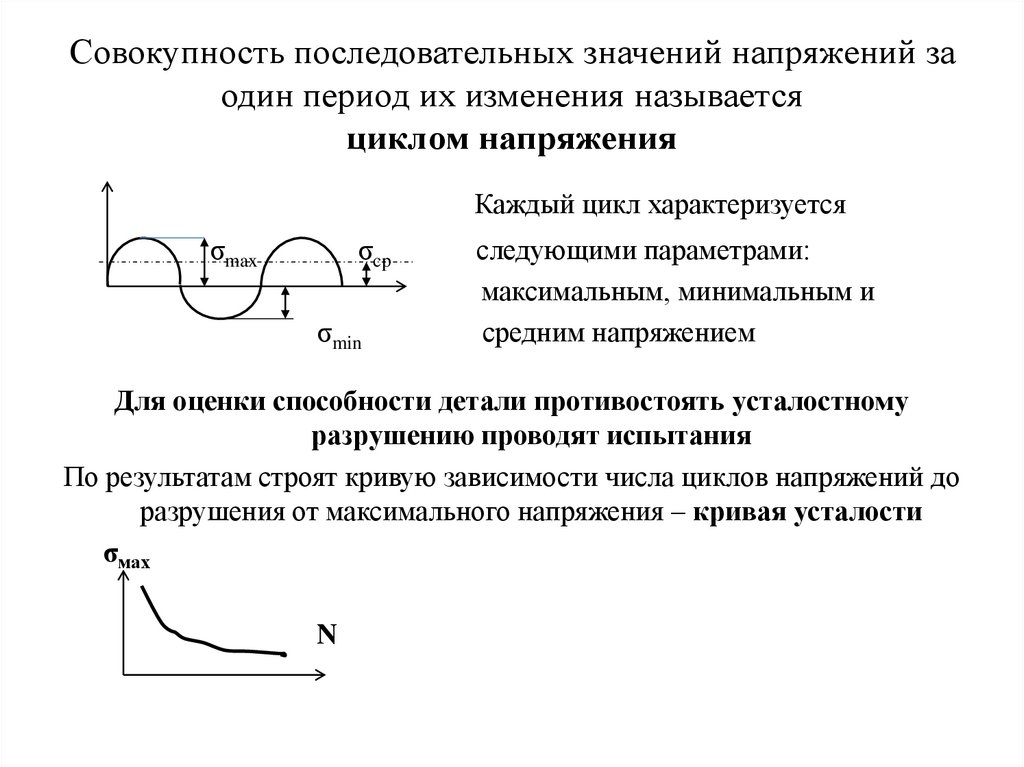
Совокупность последовательных значений напряжений за
один период их изменения называется
циклом напряжения
Каждый цикл характеризуется
σmax
σcp
σmin
следующими параметрами:
максимальным, минимальным и
средним напряжением
Для оценки способности детали противостоять усталостному
разрушению проводят испытания
По результатам строят кривую зависимости числа циклов напряжений до
разрушения от максимального напряжения – кривая усталости
σмах
N

84.

Если кривую усталости перестроить в логарифмических
координатах, то она будет иметь более простой вид
σmax
σR – предел выносливости - максимальное
напряжение при котором еще не
происходит усталостное разрушение
σRN
σR
Факторы, влияющие на снижение предела выносливости:
1. Концентрация напряжений (выточки, надрезы, отверстия, шпоночные
пазы, места резкого изменения размеров сечения);
2. Размеры поперечного сечения
3. Состояние поверхности (шероховатость, наличие коррозии, окалины и
др.)
Совместное влияние всех трех факторов учитывается введением в расчет
коэффициента снижения предела выносливости - К

85.

Прочность при динамических нагрузках
К задачам динамики в сопротивлении материалов относятся:
1. Расчеты движущихся деталей при заданных ускорениях;
2. Расчеты на действие ударной нагрузки;
3. Расчеты на прочность и жесткость при колебании.

86.

Расчет на устойчивость
Условие F≤[F]
F – действующая сила
[F]- допускаемая сила [F]=Fкр /sу
Способы определения критической силы:
1. Расчет по формуле Эйлера
Fкр=π2EJmin /(µl)2
Е – модуль продольной упругости
Jmin минимальный осевой момент инерции
l- длина
µ- коэффициент приведения длины (зависит от способа закрепления)

87.

Критические напряжения
Критическое напряжение – напряжение сжатия
соответствующее критической силе
σкр=Fкр/А=π2EJmin /(µl)2А
Jmin/А=i2min
i min -минимальный радиус инерции
Отношение µl/ imin=λ – гибкость стержня
Гибкость не зависит от материала, а зависит от геометрии стержня
σкр= π2E /λ2
Формула Эйлера выполняется только в пределах упругих деформаций
Если
λ >λ пред
λ пред =√ π2E /σпц
σпц -предел пропорциональности материала

88.

2. Расчет по формуле Ясинского
Если
λ <λ пред
Fкр=σкрA=(a-bλ)А
Порядок выполнения расчета на устойчивость
1. Рассчитываем предельную гибкость
λ пред =√ π2E /σпц
2. Считаем минимальный радиус инерции
imin=√Jmin /A
3. Считаем гибкость стержня λ=µl/imin
4. Выбор расчетных формул:
Если λ0<λ<λпред. Расчет по формуле Ясинского
Если λ>λпред расчет по формуле Эйлера

89.

Расчетно-графическая работа
Задача 1 Проверить на устойчивость стойку круглого сечения их
хромомолибденовой стали σпц=540 МПа, Е=2*105МПа, коэффициент
запаса устойчивости [sу]=2
Пункт 1-4 для круглого сечения Jx=πd4/64 А=πd2/4
imin= d/4
F≤[F]=Fкр/ [sу]
Задача 2 Для заданной стойки двутаврового сечения определить
допускаемое значение сжимающей силы - [F]. Материал стойки Ст3,
[sу]=2,0
[F]=Fкр /[sу]
По № двутавра определяем Jmin, A (таблица сортаментов)
Принимаем из таблицы 36.1 для Ст 3 λпред
Считаем минимальный радиус инерции imin=√Jmin /A
Считаем гибкость стержня λ=µl/imin
Сравниваем λ и λ пред
Выбор расчетных формул для Fкр