Similar presentations:
Открытый урок по алгебре и началам анализа в 11 классе
1. Открытый урок по алгебре и началам анализа в 11 классе
Подготовила:учитель МОУ «СОШ №4»
Г.Прохладного КБР
Лимаренко Наталия Валентиновна
2.
Бывает, что во время урока математики,когда даже воздух стынет от скуки, в
класс со двора влетает
На сегодняшнем уроке этой бабочкой окажется…
логарифмическая
функция.
3. «Логарифмическая функция и ее приложения»
Тема урока:«Логарифмическая
функция и ее
приложения»
Потому-то словно пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
Борис Слуцкий
4. Цели урока:
повторить свойства логарифмической функции;углубить знания по данной теме;
расширять представления учащихся о
логарифмической функции, применении ее
свойств в нестандартных ситуациях;
развивать интерес к истории математики и ее
практическим приложениям, логическое
мышление и математическую грамотность речи;
воспитывать познавательную активность, чувство
ответственности, культуру общения и диалога.
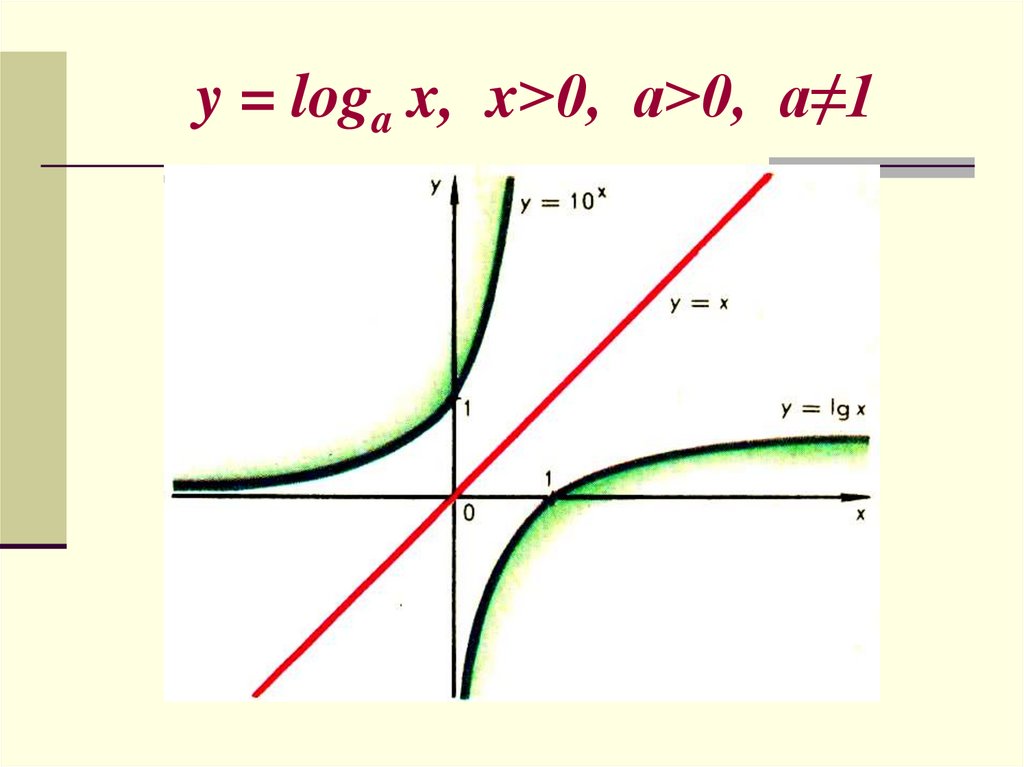
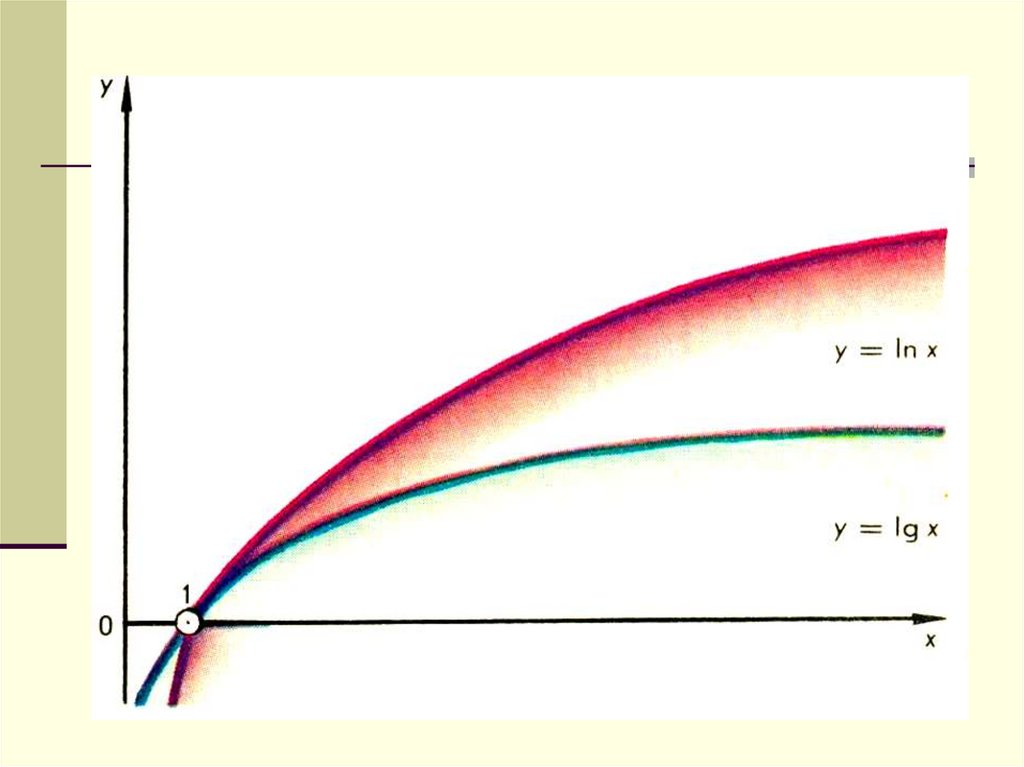
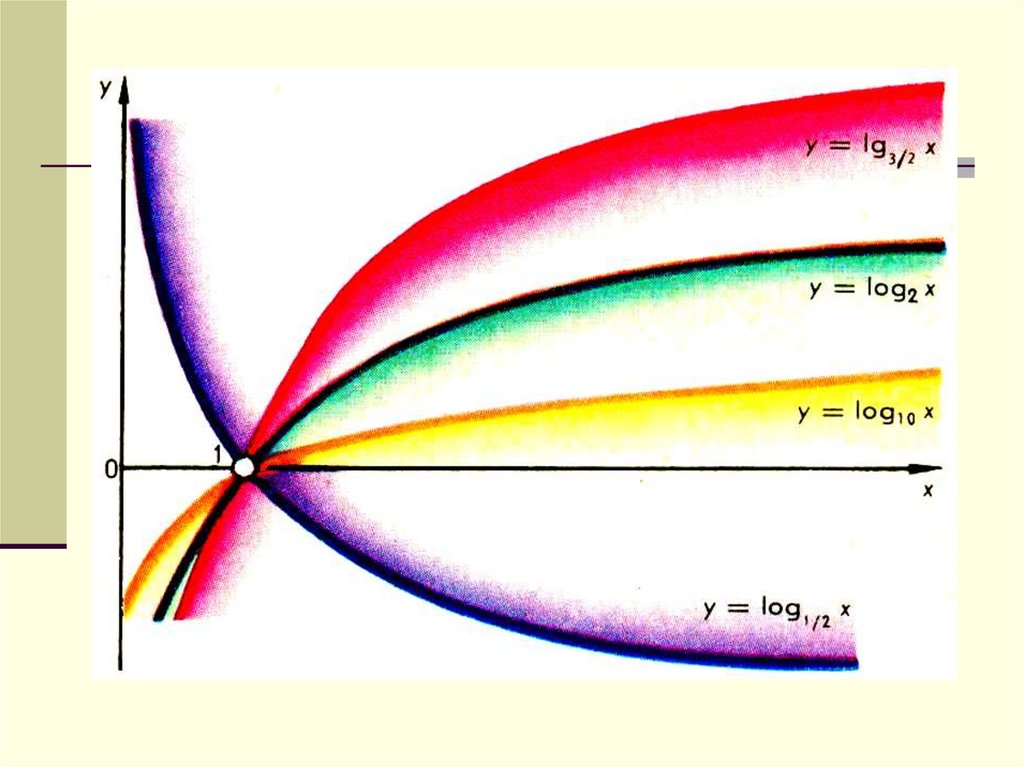
5. y = loga x, x>0, a>0, a≠1
y = loga x, x>0, a>0, a≠16.
7.
8. Прочитайте:
log a bКаким должно быть число α, каким
число b?
Какой логарифм называется
десятичным?
Какой логарифм называется
натуральным?
9. Из указанных функций назовите логарифмическую
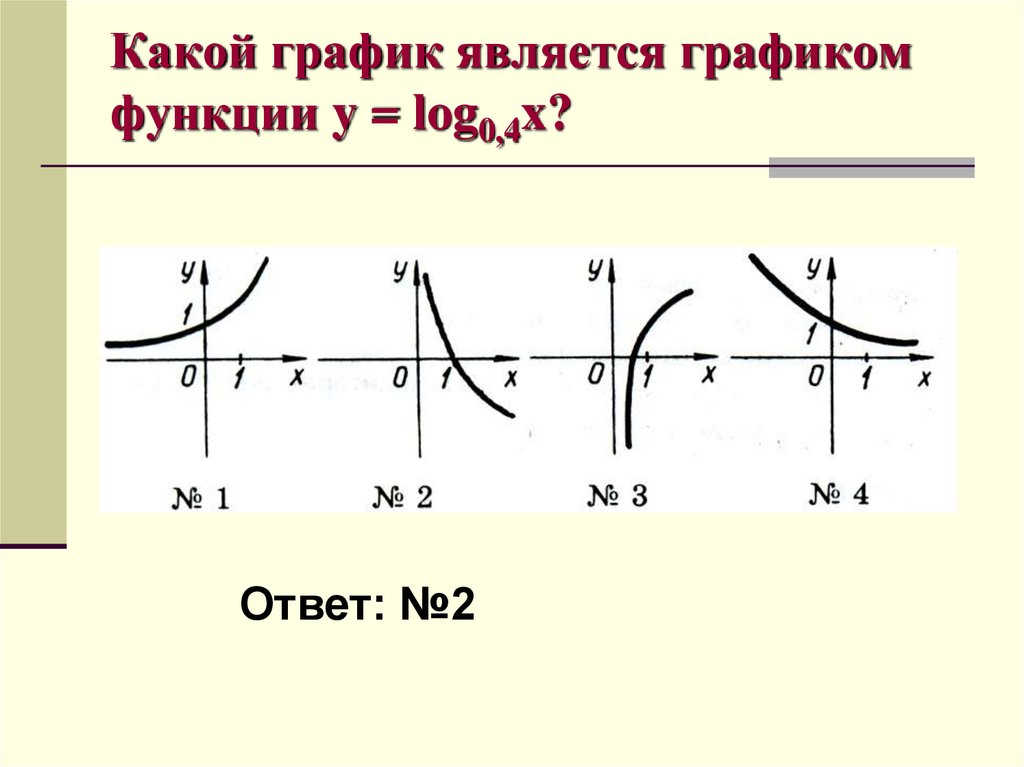
10. Какой график является графиком функции y = log0,4x?
Ответ: №211. Совпадают ли графики функций?
Ответ: 2. Нет12. При каких значениях х имеет смысл выражение:
Ответ: При x>113. Найти область определения функции y = log2(5 – 3x)
Ответ: №414. Вычислите:
Вариант 1.log 2 128,
1
log 5
,
125
log 3 27,
log 7 7,
log 5 1,
lg 0,0001,
lg 100000.
Вариант 2.
log 2 32,
1
log 2 ,
16
log 4 64,
log 3 1,
lg 10,
lg 0,001,
lg 1000000.
15. Ответы:
Вариант 1.Ответы:
Вариант 2.
16. Джон Непер
Шотландский математик изобретатель логарифмов.В 1590-х годах пришел к идее
логарифмических вычислений
и составил первые таблицы
логарифмов, однако свой
знаменитый труд “Описание
удивительных таблиц
логарифмов” опубликовал
лишь в 1614 году.
Ему принадлежит определение
логарифмов, объяснение их
свойств, таблицы логарифмов
синусов, косинусов, тангенсов и
приложения логарифмов в
сферической тригонометрии.
(1550 г.— 4 апреля 1617г.)
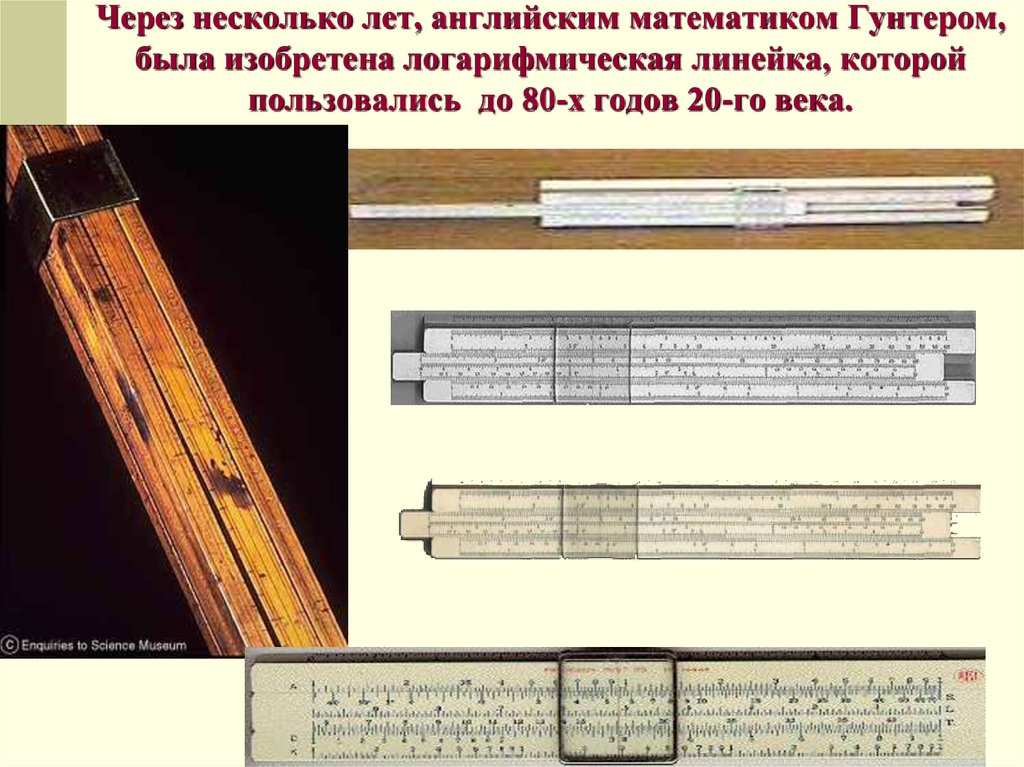
17. Через несколько лет, английским математиком Гунтером, была изобретена логарифмическая линейка, которой пользовались до 80-х
годов 20-го века.18. Задание 1. Постройте график функции:
4 x2 log2
2 x
2
y 2
19. Логарифмы в музыке
«… Даже изящные искусства питаются еюРазве музыкальная гамма не есть Набор передовых логарифмов?»
Из «Оды экспоненте»
А.А. Эйхенвальд
20. Частоту любого звука можно выразить формулой
Ноте «до» соответствует частота, равная n колебаниям в секунду.В октаве частота колебаний нижнего звука в 2 раза меньше верхнего.
Тогда ноте «до» 1-й октавы будут соответствовать 2n колебания в
секунду, а ноте «до» 3-й октавы -
n 2 m колебания в секунду и т.д.
Обозначим все ноты хроматической гаммы номерами р.
N pm n 2
2
m 12
p
21. Логарифмируя эту формулу, получаем
2lg N pm
lg N pm
lg
lg n m lg 2 p
,
12
p
lg n m lg 2.
12
22. Принимая частоту самого низкого «до» за единицу n=1 и приводя логарифмы к основанию 2, имеем
log 2 N pmp
m .
12
23. Задание 2. Решите уравнение:
52
tg x log 3 x x 0
2
24. Звезды, шум и логарифмы
По вертикальной оси отложим блеск звездв
единицах Гиппарха (распределение звезд по
субъективным характеристикам (на глаз) на 6
групп), а на горизонтальной - показания приборов.
По графику видно, что объективные и
субъективные характеристики не
пропорциональны, а прибор регистрирует
возрастание блеска не на одну и ту же величину, а
в 2,5 раза. Эта зависимость выражается
логарифмической функцией.
25. Логарифм шума
Единица измерения децибел используется в звуковой технике.Связано это с тем, что мы реагируем не на абсолютные, а на относительные
изменения уровня какого-либо воздействия, в том числе и звукового.
Если сила звука (интенсивность, I, Вт/м2) изменится в 10 раз, то субъективное
ощущение громкости — всего лишь на одну ступеньку, при 100-кратном
увеличении силы звука — на две (lg100 = 2), при 1000-кратном — на три
(lg1000 = 3). Поэтому увеличение или уменьшение силы звука принято
измерять в логарифмических единицах, и каждое десятикратное изменение
силы звука оценивается единицей, называемой Бел (Б).
На практике используется в основном единица, равная десятой части
Бела - децибел.
Значение в децибелах равно десяти десятичным логарифмам отношения
интенсивностей двух сигналов.
26. Физкультминутка
Молодцы! Пора за работу! Удачи!27. Логарифмическая «комедия» 2>3
Логарифмическая«комедия» 2>3
Комедия начинается с неравенства 1 1 , бесспорно
4 8
правильного.
2
3
1 1
Затем следует преобразование , тоже не
2 2
внушающее сомнения.
Большему числу соответствует больший логарифм,
2
3
значит,
1
1
1
1
2 lg 3 lg .
lg lg ,
2
2
2
2
1
имеем 2 3.
После сокращения на lg
2
В чем ошибка этого доказательства?
28.
Логарифмическая спиральНа рисунке видно, что эта спираль пересекает все прямые,
проходящие через полюс под одним и тем же углом.
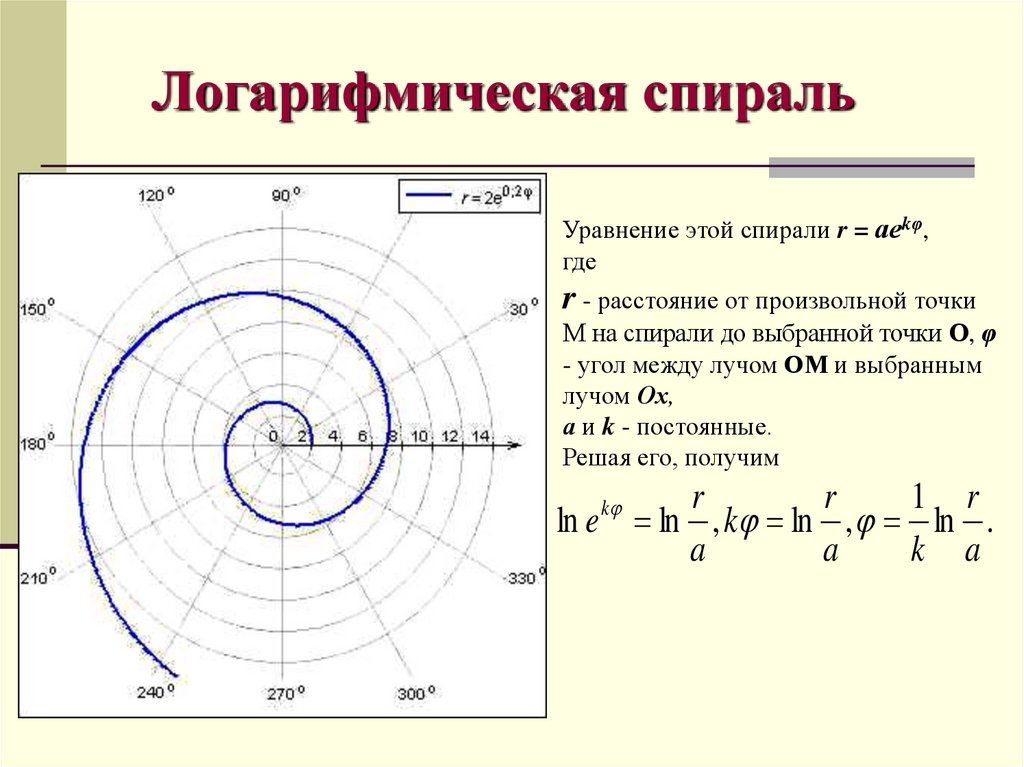
29. Логарифмическая спираль
Уравнение этой спирали r = аеkφ,где
r - расстояние от произвольной точки
М на спирали до выбранной точки О, φ
- угол между лучом ОМ и выбранным
лучом Ох,
а и k - постоянные.
Решая его, получим
r
r
1 r
ln e ln , k ln , ln .
a
a
k a
k
30. Логарифмическая спираль
Раковины морских животных могут расти лишь в одномнаправлении. Чтобы не слишком вытягиваться в длину, им
приходится скручиваться, причем каждый следующий виток
подобен предыдущему. А такой рост может совершаться лишь
по логарифмической спирали или ее аналогиям. Поэтому
раковины многих моллюсков, улиток, закручены по
логарифмической спирали.
31. Логарифмическая спираль
Рога таких животных, как архары,закручены по логарифмической
спирали.
В подсолнухе семечки
расположены по дугам,
близким к
логарифмической
спирали
32.
По логарифмической спиралиформируется и тело циклона
33.
По логарифмическим спиралям закручены и многие галактики, вчастности – Галактика, которой принадлежит Солнечная система.
34. Решите неравенство:
log x 0,5 3 x 135. Творческое задание: «Логарифмическая диковинка»
Число 3 изобразить с помощью трехдвоек и математических символов.
Решение:
Ответ:
36. Домашнее задание:
на «3» выполнить 1), 2) и 3) задания;на «4» и на «5» - все задания.
37. Подведём итоги
38. Рефлексия
В связи с чем возникла необходимость влогарифмах?
Что нового вы узнали о логарифмической
функции и ее приложениях?
Кого из учёных, внёсших вклад в развитие
логарифмов, вы запомнили?
Что надо учитывать, решая различные задания с
логарифмами?
Спасибо за работу! Удачи!
































 mathematics
mathematics








