Similar presentations:
Случайная изменчивость. Частота значений в массиве данных
1.
21.02.2024Случайная изменчивость
Частота значений в массиве данных.
1
2.
ПовторениеВыполните задание:
Список финалистов чемпионатов мира по
футболу с 1930 года: Аргентина,
Чехословакия, Венгрия, Бразилия,
Венгрия, Швеция, Чехословакия, ФРГ,
Италия, Нидерланды, Нидерланды, ФРГ,
ФРГ, Аргентина, Италия, Бразилия,
Германия, Франция
Найти :
1) объём ряда
2) моду ряда
3) составьте таблицу распределения
2
3.
Частота случайного событияТеория вероятностей имеет дело с экспериментами, исходы которых непредсказуемы:
они зависят от случая. Чтобы выяснить, насколько вероятно то или иное случайное
событие, нужно вычислить, как часто оно происходит. Для этого используют важные
величины: абсолютную и относительную частоту.
Абсолютная частота показывает, сколько раз в серии
экспериментов наблюдалось данное событие.
Относительная частота показывает, какая доля
экспериментов завершилась наступлением данного исхода.
Частота представляет собой число повторений, сколько раз за
какой-то период происходило некоторое событие, проявлялось
определенное свойство объекта, либо наблюдаемый параметр
достигал данной величины.
То есть частота определяет то, как часто повторяется та или
иная величина в выборке.
3
4.
Частота результата = (сколько разрезультат встретился) : (объем данного
ряда)
Например:
среди 19 данных некоторого измерения один
и тот же результат встретился 5 раз.
Значит частота данного результата равна
5:19
4
5.
Процентная частота = (частота · 100% )Например:
если частота результата равна
5:19= 0,263157…,
то процентная частота будет равна:
0,263 · 100 = 26,3%
Часто ответы для процентных частот могут
быть не точными, а приближенными
5
6.
Пример 1.Юный
математик
Петя
на
праздники ездил с родителями
на машине на дачу к бабушке.
Дорога была долгая, и Петя от
скуки начал подсчитывать цвета
встречных машин. Результаты
подсчетов – в таблице. Найдите
частоту события:
а) «Пете встретилась синяя
машина»;
б) «Пете встретилась не черная
машина»;
в) «Пете встретилась красная
или зеленая машина».
Ответы: а) 0,2; б) 0,72; в) 0,16.
Цвет
машины
Количе
ство
Черный
21
Белый
17
Красный
9
Коричневый
10
Синий
15
Зеленый
3
6
7.
Пример 2.Малая выборка. В таблице 2 приведены результаты исследования – измерения
роста двадцати случайно выбранных девушек, живущих в Москве.
Табл. 2 Рост девушек, см (малая выборка)
164
167
170
164
160
168
163
164
Найти :
1) объём ряда
2) размах
3) среднее значение
4) медиана
170
167
171
165
166
164
169
158
166
159
165
167
В выборке
1) обьём ряда 20,
2) размах значений равен 13:
рост колеблется между 158 и 171 см.
3) среднее значение роста равно
165,35,
4) медиана – 165,5.
7
8.
Пример 2.Табл. 2 Рост девушек, см (малая выборка)
164
167
170
164
160
168
163
164
170
167
171
165
166
164
169
158
166
159
165
167
Частота – это число повторений какой-либо величины параметра.
В нашем случае, это можно считать вот так.
Сколько девушек с ростом 169 см?
Одна. Таким образом, частота встречи девушки с ростом 169 в нашей выборке
равна 1.
Сколько девушек имеет рост 163?
Одна. Частота встречи девушки с ростом 163 в нашей выборке равна 1.
Табл. 3 Группировка данных и нахождение частот (малая выборка)
158 159 160 161 162 163 164 165 166 167 168 169 170 171
1
1
1
0
0
1
4
2
2
3
1
1
2
1
8
9.
Табл. 3 Группировка данных и нахождение частот (малая выборка)158
159
160
161
162
163
164
165
166
167
168
169
170
171
1
1
1
0
0
1
4
2
2
3
1
1
2
1
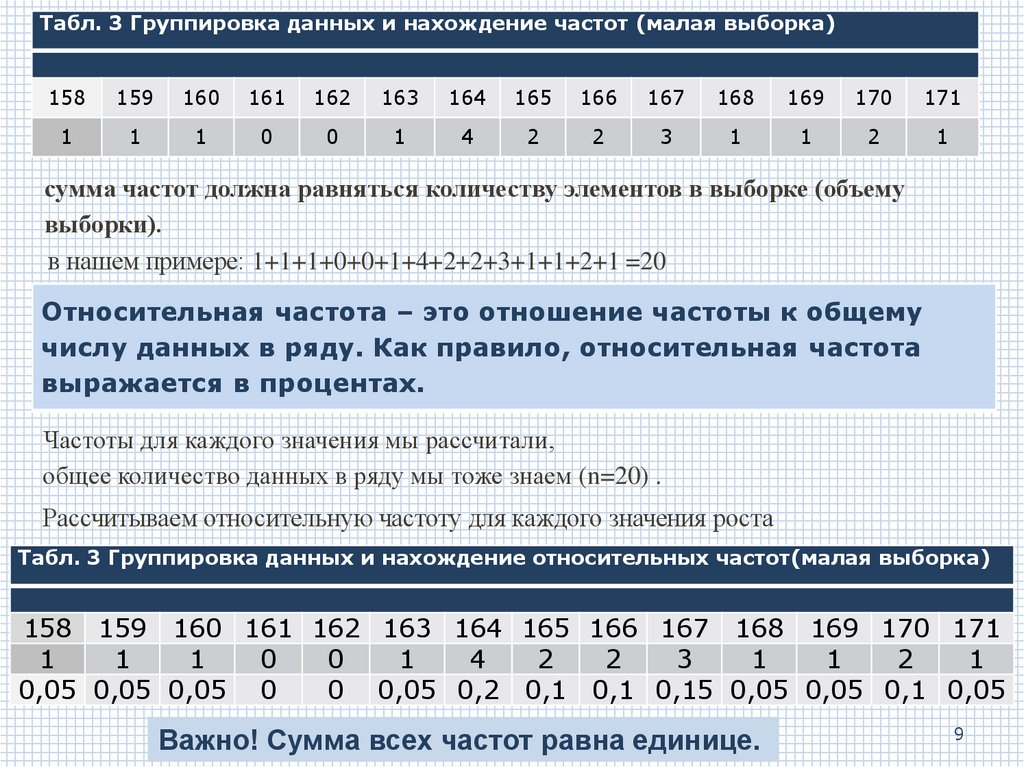
сумма частот должна равняться количеству элементов в выборке (объему
выборки).
в нашем примере: 1+1+1+0+0+1+4+2+2+3+1+1+2+1 =20
Относительная частота – это отношение частоты к общему
числу данных в ряду. Как правило, относительная частота
выражается в процентах.
Частоты для каждого значения мы рассчитали,
общее количество данных в ряду мы тоже знаем (n=20) .
Рассчитываем относительную частоту для каждого значения роста
Табл. 3 Группировка данных и нахождение относительных частот(малая выборка)
158 159 160 161 162 163 164 165 166 167 168 169 170 171
1
1
1
0
0
1
4
2
2
3
1
1
2
1
0,05 0,05 0,05 0
0 0,05 0,2 0,1 0,1 0,15 0,05 0,05 0,1 0,05
Важно! Сумма всех частот равна единице.
9
10.
Средняя выборка. Пополним наблюдения. К двадцати значениямПример 3. добавим ещё тридцать (см. таблицу4).
самостоятельно составь таблицы частот и относительных частот для
примера средней выборки
Табл. 4 Рост девушек, см (средняявыборка)
164
170
160
163
170
171
166
169
166
165
167
164
168
164
167
165
164
158
159
167
161
169
162
170
168
165
165
166
164
173
158
166
168
167
161
167
165
168
165
164
163
169
161
162
163
160
166
169
172
160
Среднее значение роста в этойвыборке равно 165,3 см, а медиана –165 см.
Эти значения мало отличаются от тех, что были полученына малой выборке.
А размах вырос до 15 см. Это естественно: чем больше выборка, тем выше шансы, что
в нее попадут очень высокие и очень низкие люди. Поэтому размах увеличивается, а
среднее значение устойчиво.
10
n=50
11.
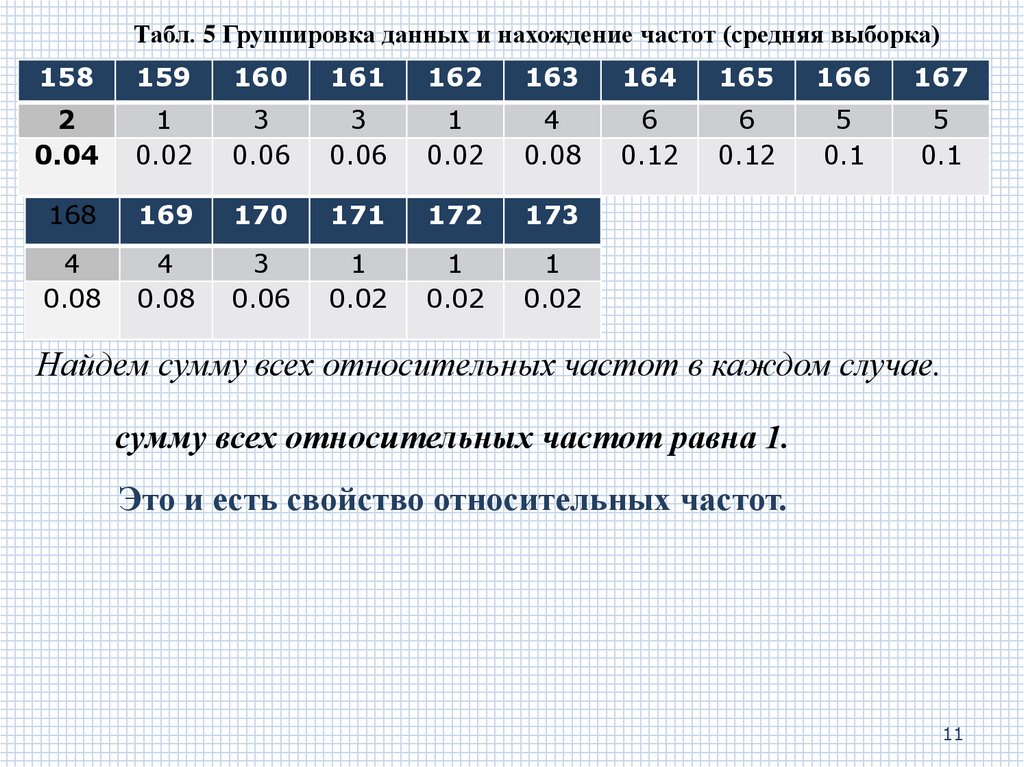
Табл. 5 Группировка данных и нахождение частот (средняя выборка)158
159
160
161
162
163
164
165
166
167
2
0.04
1
0.02
3
0.06
3
0.06
1
0.02
4
0.08
6
0.12
6
0.12
5
0.1
5
0.1
168
169
170
171
172
173
4
0.08
4
0.08
3
0.06
1
0.02
1
0.02
1
0.02
Найдем сумму всех относительных частот в каждом случае.
сумму всех относительных частот равна 1.
Это и есть свойство относительных частот.
11
12.
Группировка данных – применяется когда различныхрезультатов измерений слишком много.
Т.е. их объединяют в группы.
При группировке различных данных информация
становится менее точной.
12
13.
21.02.2024Домашнее задание
Рассеянные жители столицы не имеют понятия о многих впечатлениях, столь известных
жителям деревень или городков, например, об ожидании почтового дня: во вторник и
пятницу полковая наша канцелярия бывала полна офицерами: кто ждал денег, кто
письма, кто газет
А) Посчитайте буквы «а», «о» и «и» в этих отрывках т составьте таблицу частот.
Б) Посчитайте буквы «и» и «т» и составьте таблицу частот. Можно ли по полученным
данным судить , какая из букв «и» или «т»- используется чаще в русском языке?
13











 mathematics
mathematics








