Дифракция. Принцип Гюйгенса-Френеля

1. Дифракция

Дифракцией называется явление отклонения света
от прямолинейности распространения, огибание
им малых препятствий, проникновение в область
геометрической тени.
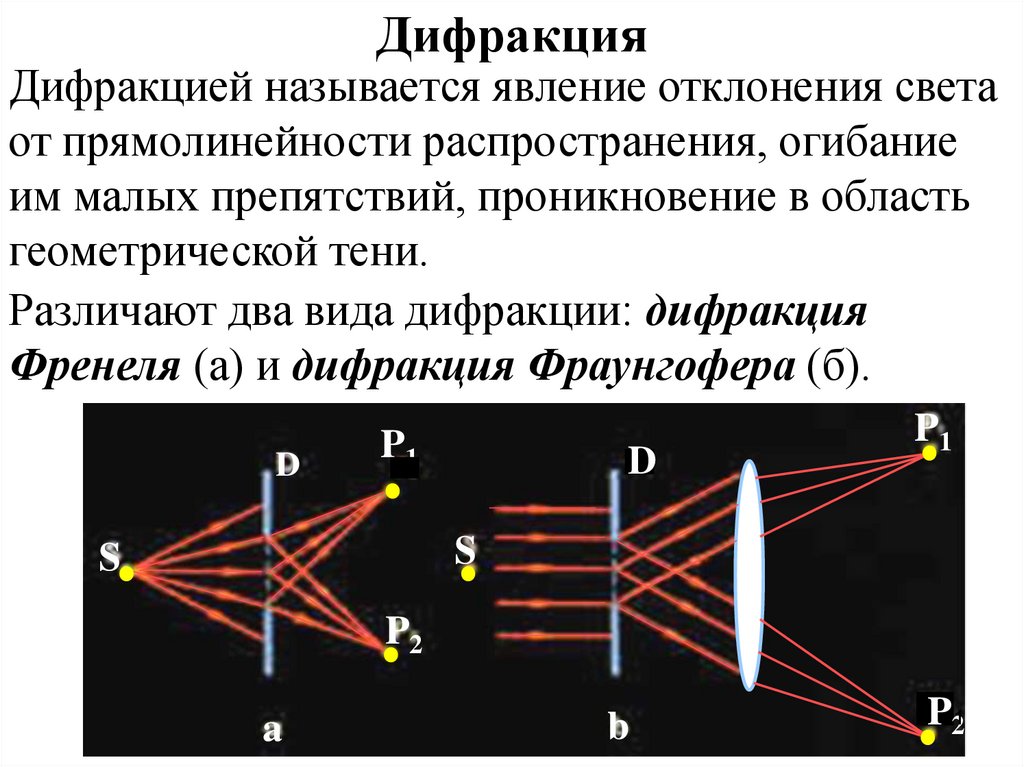
Различают два вида дифракции: дифракция
Френеля (а) и дифракция Фраунгофера (б).
D
P1
D
P1
S
S
P2
a
b
P21

2.

Принцип Гюйгенса–Френеля
1) Принцип Гюйгенса:
Каждая точка фронта волны, служит источником
вторичных волн, распространяющихся с характерной для
данной среды скоростью.
2) Принцип интерференции: Все точки фронта волны
колеблются с одинаковой частотой и в одинаковой фазе и,
следовательно,
представляют
собой
когерентные
источники. Волны от этих источников распространяются
только вперёд и интерферируют между собой.
3) Если часть волнового фронта прикрыть непрозрачными
экранами, то вторичные волны испускают только
открытые участки фронта волны, причём так, как при
отсутствии экранов.
4) Мощности излучения равных по площади участков
2
фронта волны равны.

3. Метод зон Френеля

Пусть поверхность S положение волнового фронта
в некоторый момент. Чтобы
определить колебания в
некоторой
точке
P,
вызванные волной, нужно
определить
колебания,
вызываемые в этой точке
отдельными
вторичными
волнами, приходящими в нее
от всех элементов поверхности S (ΔS1, ΔS2 и т. д.), и
затем сложить эти колебания с учетом их амплитуд и фаз.
Метод зон Френеля позволяет упростить этот расчёт. 3

4.

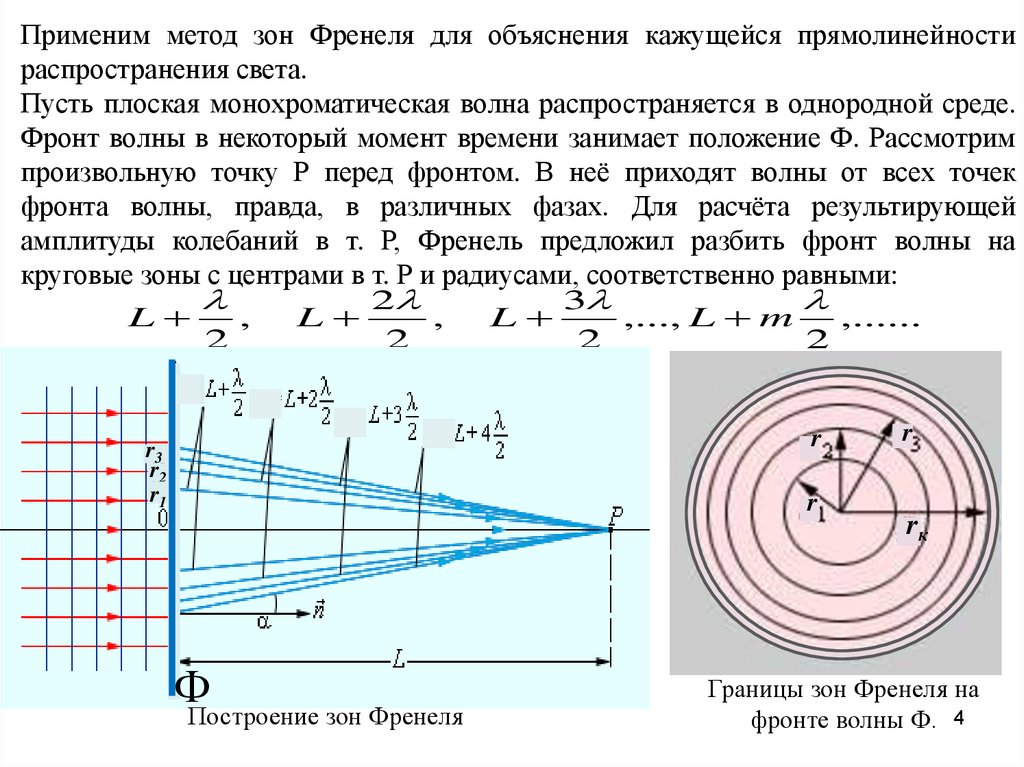
Применим метод зон Френеля для объяснения кажущейся прямолинейности
распространения света.
Пусть плоская монохроматическая волна распространяется в однородной среде.
Фронт волны в некоторый момент времени занимает положение Ф. Рассмотрим
произвольную точку Р перед фронтом. В неё приходят волны от всех точек
фронта волны, правда, в различных фазах. Для расчёта результирующей
амплитуды колебаний в т. Р, Френель предложил разбить фронт волны на
круговые зоны с центрами в т. Р и радиусами, соответственно равными:
2
3
L
,
L
,
L
,..., L m
,......
2
2
2
2
r
r3
r2
r1
r
ФПостроение зон Френеля
r
rк
Границы зон Френеля на
фронте волны Ф. 4

5.

Таким образом, колебания от 2-х соседних зон приходят
в т. Р с разностью хода λ/2, т.е. в противофазах.
Обозначим амплитуды колебаний, приходящих от
каждой зоны в точку Р,
А1, А2, А3, А4,………
Тогда результирующая амплитуда в точке Р:
А = А1 – А2 + А3 – А4 + ………
Амплитуды колебаний от каждой зоны в точке Р:
A1 > A2 > A3 > ... > Aт >…
Можно допустить:
Результирующую амплитуду представим в виде:
А3 А3
А5 А5
А1 А1
А
А2
А4
...
5
2 2
2 2
2 2

6.

Т.к. выражения в скобках обращаются в 0, то
А1
Ап
,
если п - нечётное
2
2
А=
A1
Aп 1
если п – чётное
Aп ,
2
2
где п – номер последней зоны.
Т.к. п велико, Ап-1 и Ап << А1 , и практически А = А1/2,
т.е. в точке Р амплитуда колебаний такая же, как от
половины первой зоны Френеля.
Т. к. радиус первой зоны мал, то при полностью
открытом фронте волны (свет распространяется без
преград)
свет
кажется
распространяющимся
6
прямолинейно, дифракция не наблюдается.

7.

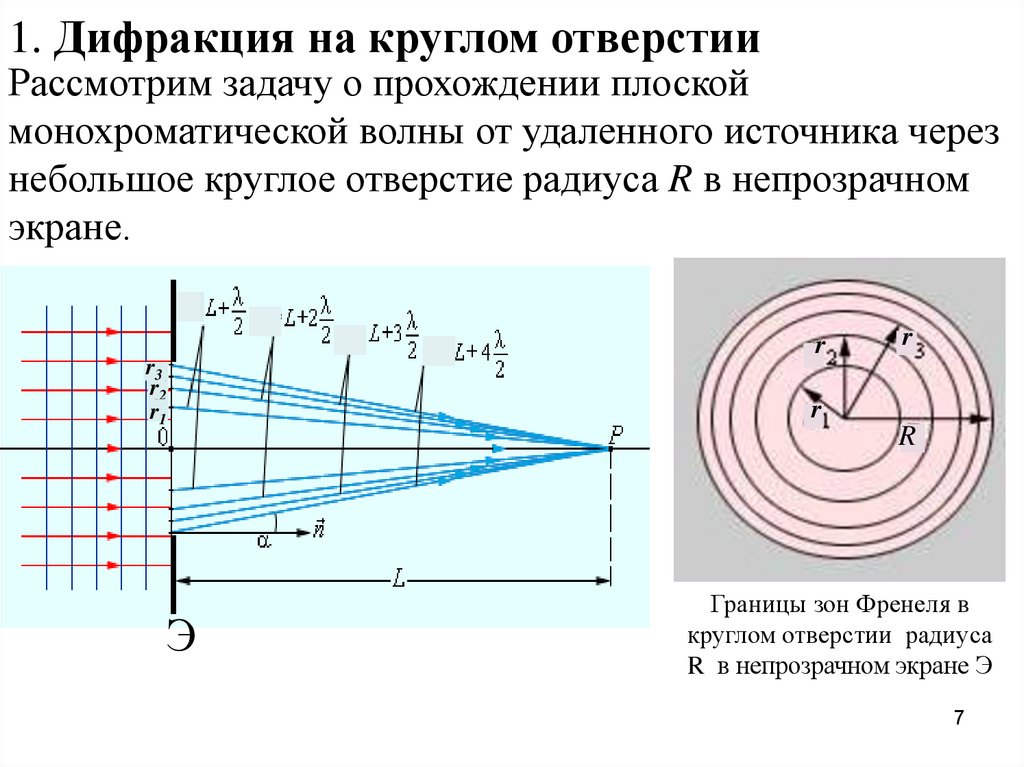
1. Дифракция на круглом отверстии
Рассмотрим задачу о прохождении плоской
монохроматической волны от удаленного источника через
небольшое круглое отверстие радиуса R в непрозрачном
экране.
r
r3
r2
r1
Э
r
r
R
Границы зон Френеля в
круглом отверстии радиуса
R в непрозрачном экране Э
7

8.

Рассчитаем радиус m – ой зоны Френеля rт :
2
2
rm ( L m ) L m L m
m L
2
4
2
2
Количество зон Френеля ттах, укладывающихся в
отверстии, зависит от радиуса отверстия R:
2
R
mтах
.
L
Определим амплитуду колебаний в точке Р экрана:
8

9.

A = A1 – A2 + A3 – A4 + ... . ± Аm, где т номер
последней
зоны,
укладывающейся
в
отверстии.
Если m – чётное, то в т. Р – минимум освещённости,
т.к. колебания от соседних зон попарно гасят друг друга.
Если m – нечётное, то в т. Р – максимум освещённости,
т.к. действие последней, нечётной зоны окажется не
скомпенсированным.
Из соображений симметрии и из закона сохранения
энергии очевидно, что вокруг точки Р будут наблюдаться
чередующиеся светлые и тёмные кольца с центром в т. Р,
то есть имеет место дифракция света.
Если диаметр отверстия 2 R очень велик, то Аm<< А1 и
результат будет такой же, как при полностью открытом
9
фронте волны, т.е. дифракция наблюдаться не будет.

10. Дифракция на круглом непрозрачном диске

При дифракции света на круглом диске закрытыми
оказываются зоны Френеля первых номеров от 1 до m.
Тогда амплитуда колебаний в точке наблюдения будет
равна :
Аm 1 Аm 1
Аm 3 Аm 3
Аm 5
А
Аm 2
Аm 4
2 2
2 2
2
Am 1
Аm 5
...
,
2
2
т.к. выражения в скобках = 0.
Т.об., если размеры диска невелики, то в центре экрана
интерференционный максимум – пятно Пуассона,
окруженное темными и светлыми дифракционными
10
кольцами.

11. Дифракция от одной щели

Условие минимума :
a sin 2m m ,
2
где m = 1, 2, 3, …
Условие максимума:
a sin ( 2m 1)
2
11

12.

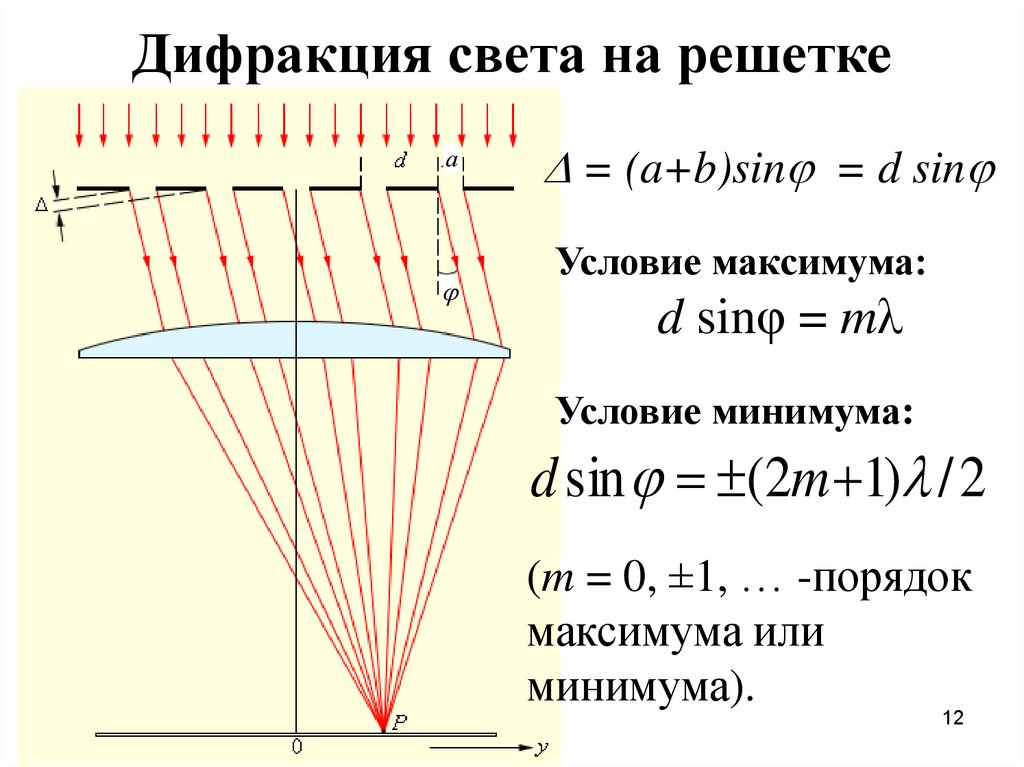
Дифракция света на решетке
а
= (a+b)sin = d sin
Условие максимума:
d sinφ = mλ
Условие минимума:
d sin (2m 1) / 2
(m = 0, ±1, … -порядок
максимума или
минимума).
12

13.

Если на решётку падает монохроматический свет, то на
экране
наблюдаются
чередующиеся
светлые
(соответствующей окраски) и тёмные полосы.
Если на решётку падает белый свет, то в центре экрана
белая полоса, по обе стороны от которой будут
располагаться спектры, начинающиеся фиолетовым и
заканчивающиеся красным светом.
т - порядок спектра.
Центральная белая полоса – максимум нулевого порядка.
Разрешающая способность решётки R – способность
решётки разделять две близкие длины волн λ и λ+Δλ:
R = λ/Δλ = т N
N – полное число щелей (штрихов) решётки,
т – порядок спектра
13

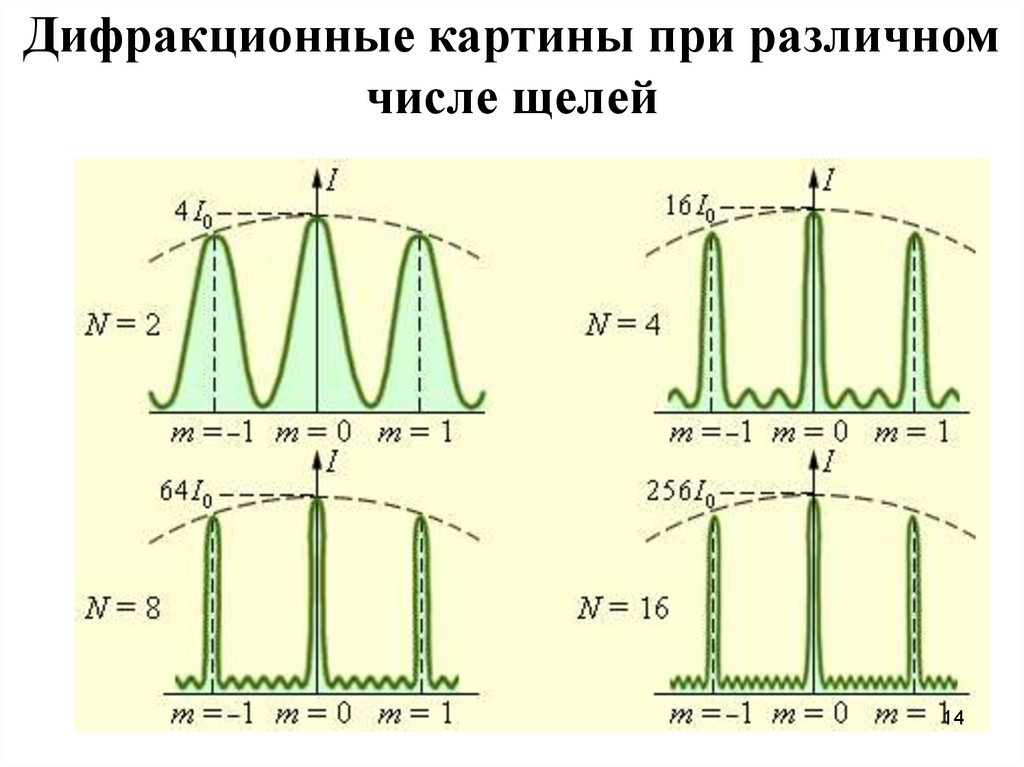
14.

Дифракционные картины при различном
числе щелей
14