Дифракция света. Принцип Гюйгенса-Френеля. Лекция 16(1)

1. Лекция 16. Дифракция света. Принцип Гюйгенса-Френеля

2.

Вопросы:
Принцип Гюйгенса – Френеля
Метод зон Френеля. Векторная диаграмма
Дифракция Френеля от круглого отверстия (и
от круглого диска)
Дифракция Фраунгофера от щели
Предельный переход от волновой оптики к
геометрической

3. Принцип Гюйгенса - Френеля

• Краткое введение в дифракцию света
Под дифракцией света понимают совокупность явлений,
наблюдаемых при распространении световых волн в среде с
резкими неоднородностями (края экранов, отверстия в
непрозрачных телах и т.п.) и связанных с отклонениями от
законов геометрической оптики. Дифракция приводит к
огибанию световыми волнами непрозрачных преград и
проникновению света в область геометрической тени.
Для наблюдения дифракции световых волн необходимо
создание специальных условий, обусловленных малостью
длин λ этих волн.
Между интерференцией и дифракцией нет существенного
физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции
волн.
В
основном
по
историческим
причинам,
перераспределение интенсивности, возникающее в результате
наложения волн, возбуждаемых конечным числом дискретных
когерентных источников, называют интерференцией. А перераспределение интенсивности, возникающее вследствие
наложения
волн
–
от
когерентных
источников,
расположенных непрерывно, называют дифракцией волн.

4. Принцип Гюйгенса - Френеля

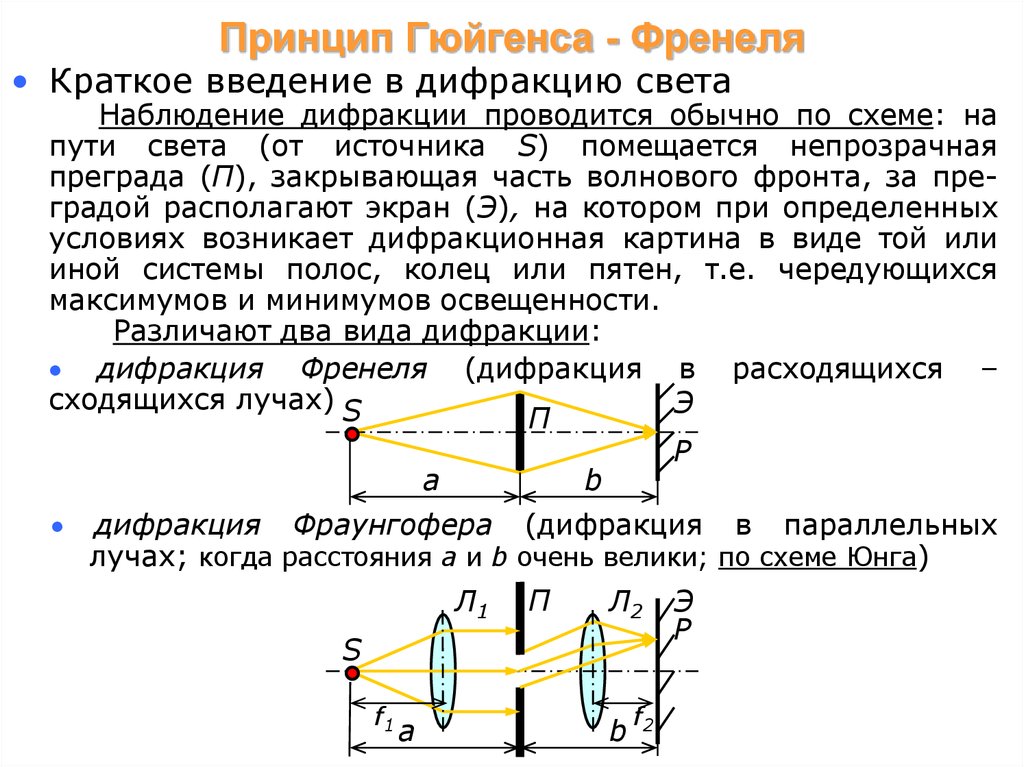
• Краткое введение в дифракцию света
Наблюдение дифракции проводится обычно по схеме: на
пути света (от источника S) помещается непрозрачная
преграда (П), закрывающая часть волнового фронта, за преградой располагают экран (Э), на котором при определенных
условиях возникает дифракционная картина в виде той или
иной системы полос, колец или пятен, т.е. чередующихся
максимумов и минимумов освещенности.
Различают два вида дифракции:
дифракция Френеля (дифракция в расходящихся –
сходящихся лучах) S
Э
П
Р
a
b
дифракция Фраунгофера (дифракция в параллельных
лучах; когда расстояния а и b очень велики; по схеме Юнга)
Л1
П
Л2
S
f1
a
b
f2
Э
Р

5. Принцип Гюйгенса - Френеля

• Основной принцип волновой оптики
Расчет интерференционно-дифракционной картины, т.е.
определение закона распределения интенсивности света,
можно провести точно путем решения системы уравнений
Максвелла при известных граничных условиях, однако это
будет связано с большими математическими трудностями. На
практике часто оказывается вполне достаточным приближенный метод решения этой задачи, основанный на принципе
Гюйгенса – Френеля. Этот принцип является основным
постулатом
волновой
теории,
описывающим
механизм
распространения и взаимодействия (наложения) волн.
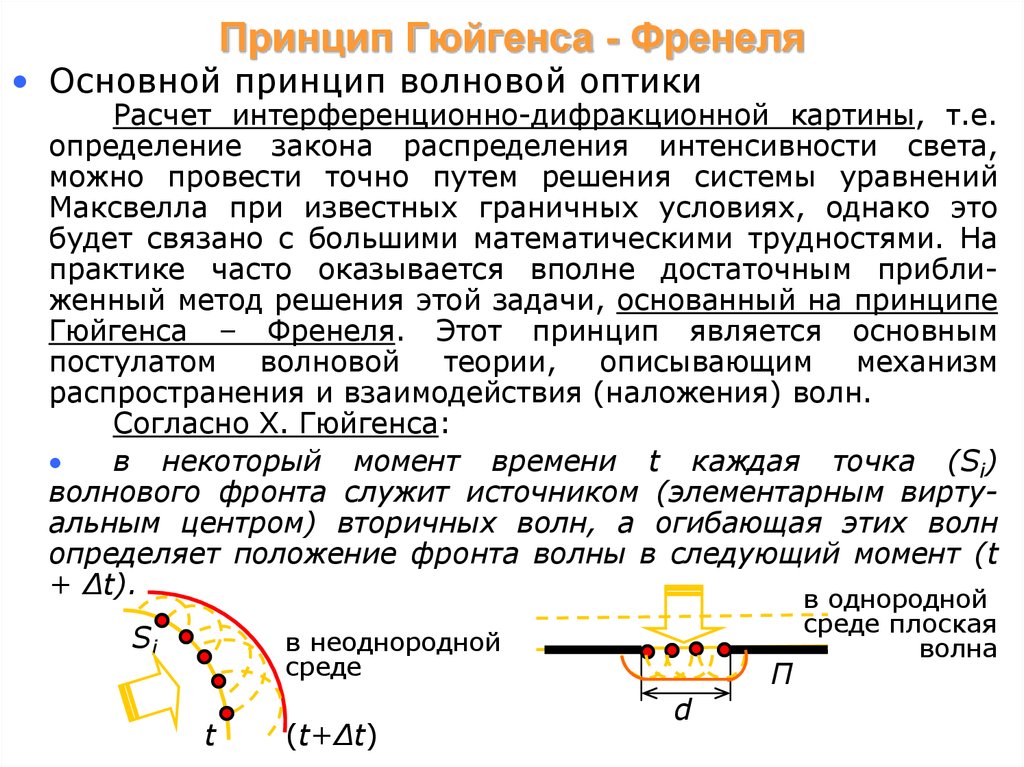
Согласно Х. Гюйгенса:
в некоторый момент времени t каждая точка (Si)
волнового фронта служит источником (элементарным виртуальным центром) вторичных волн, а огибающая этих волн
определяет положение фронта волны в следующий момент (t
+ Δt).
в однородной
Si
в неоднородной
среде
t
(t+Δt)
П
d
среде плоская
волна

6. Принцип Гюйгенса - Френеля

• Основной принцип волновой оптики
О. Френель дополнил принцип Гюйгенса представлением
об интерференции вторичных волн:
так как все вторичные источники принадлежат одной
волновой поверхности, то они – когерентны, и следовательно,
волны, вызванные их действием, при наложении могут
интерферировать и определять соответствующий интерференционный результат за пределами поверхности.
Рассмотрим непрозрачный экран (Э) с некоторым
отверстием (S), через которое проходит свет от точечного
монохроматического источника S0; требуется определить
напряженность Е светового вектора (или амплитуду колебания
АР) в точке Р перед экраном (куда еще на данный момент
волна не дошла).
Согласно
принципа
ГюйгенсаЭ
k Френеля каждый элемент dS волновой
поверхности S, открытый отверстием
экрана, служит источником вторичной
dS
сферической
волны,
амплитуда
S
S
P
r
которой пропорциональна величине
S0
dS и амплитуде первичной волны а0,
пришедшей к этому элементу.

7. Принцип Гюйгенса - Френеля

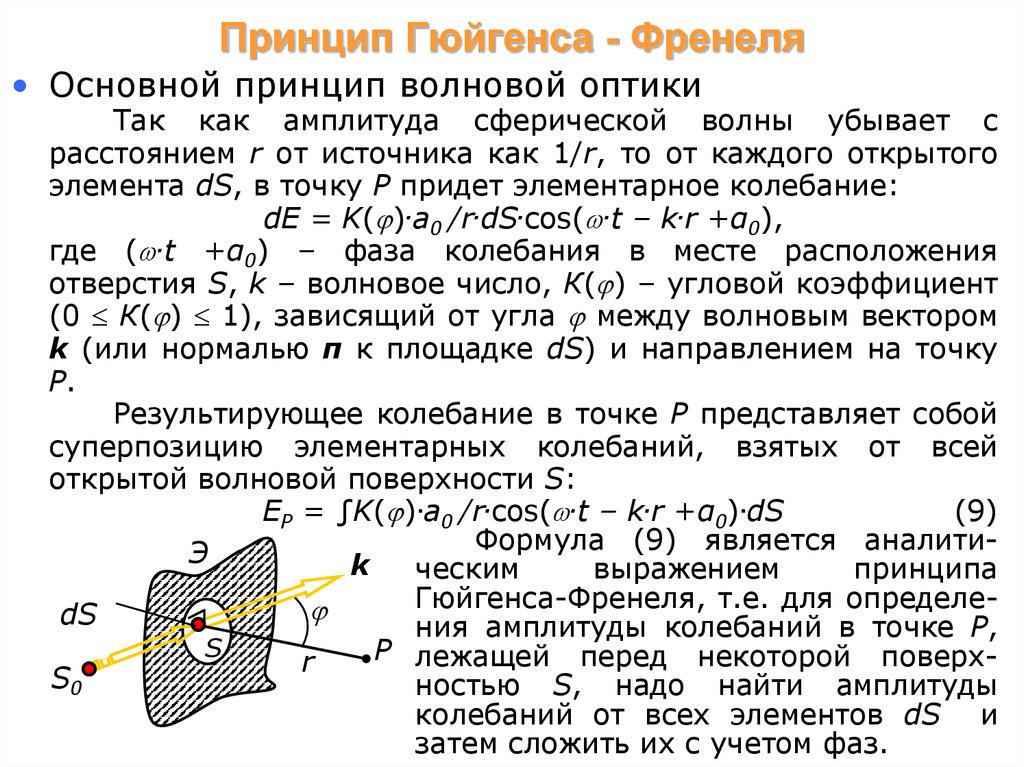
• Основной принцип волновой оптики
Так как амплитуда сферической волны убывает с
расстоянием r от источника как 1/r, то от каждого открытого
элемента dS, в точку Р придет элементарное колебание:
dE = K( ).a0 /r.dS.cos( .t – k.r +α0),
где ( .t +α0) – фаза колебания в месте расположения
отверстия S, k – волновое число, К( ) – угловой коэффициент
(0 К( ) 1), зависящий от угла между волновым вектором
k (или нормалью п к площадке dS) и направлением на точку
Р.
Результирующее колебание в точке Р представляет собой
суперпозицию элементарных колебаний, взятых от всей
открытой волновой поверхности S:
EP = ∫K( ).a0 /r.cos( .t – k.r +α0).dS
(9)
Формула (9) является аналитиЭ
k
ческим
выражением
принципа
Гюйгенса-Френеля, т.е. для определе
dS
ния амплитуды колебаний в точке Р,
S
S
P лежащей перед некоторой поверхr
S0
ностью S, надо найти амплитуды
колебаний от всех элементов dS и
затем сложить их с учетом фаз.

8. Метод зон Френеля. Векторная диаграмма

• Расчет размеров зон Френеля
Вычисления по формуле (9), вообще, достаточно сложны.
Однако, как показал Френель, в случаях, отличающихся
определенной
симметрией,
нахождение
амплитуды
результирующего колебания может быть осуществлено
простым алгебраическим или геометрическим суммированием.
Френель предложил разбивать открытую волновую
поверхность на зоны, конфигурация которых зависит от
симметрии рассматриваемой задачи.
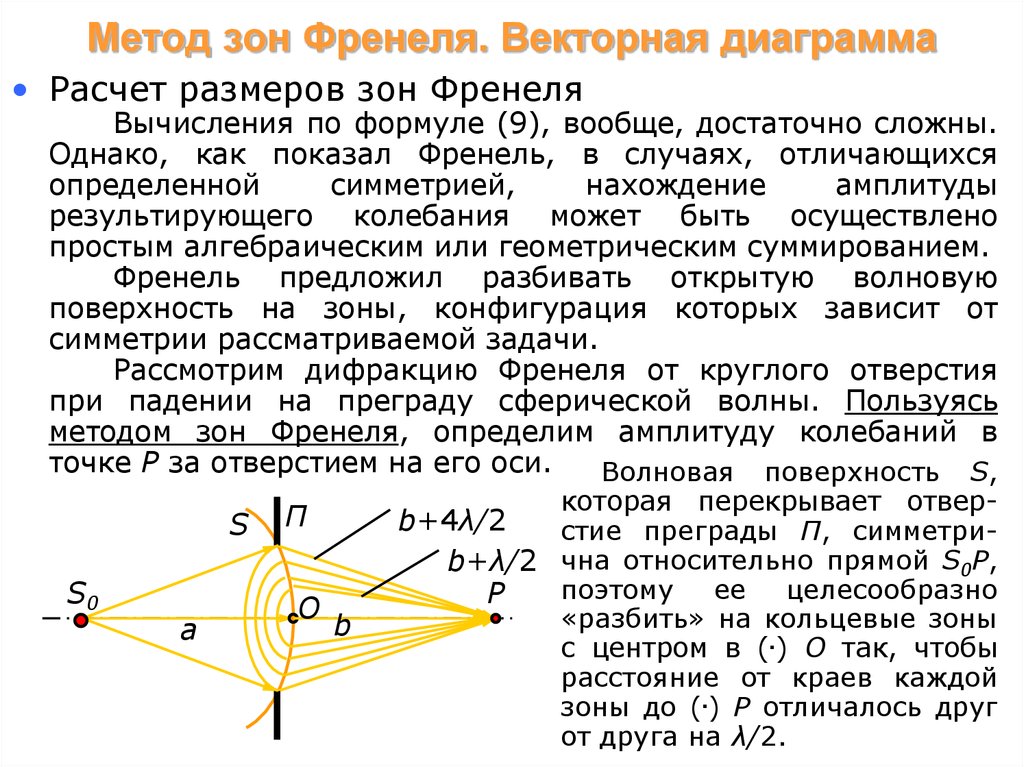
Рассмотрим дифракцию Френеля от круглого отверстия
при падении на преграду сферической волны. Пользуясь
методом зон Френеля, определим амплитуду колебаний в
точке Р за отверстием на его оси.
Волновая поверхность S,
S
S0
a
П
O
b
которая перекрывает отверb+4λ/2
стие преграды П, симметриb+λ/2 чна относительно прямой S0P,
поэтому ее целесообразно
P
«разбить» на кольцевые зоны
с центром в (.) О так, чтобы
расстояние от краев каждой
зоны до (.) Р отличалось друг
от друга на λ/2.

9. Метод зон Френеля. Векторная диаграмма

• Расчет размеров зон Френеля
Определение. Симметричные относительно оптической
оси зоны, на которые можно «разбить» свободный волновой
фронт и расстояния от границ которых до точки наблюдения
отличаются друг от друга на полволны (а колебания,
приносимые в эту точку соответствующими световыми лучами,
находятся в противофазе), называются зонами Френеля.
Определим внешний радиус m-ой зоны Френеля rm. Для
этого найдем отрезок СО = ha+ hb = m.λ/2. Из рисунка видно,
что для ΔS0AB: rm2 = a2- (a – ha)2= (2a – ha).ha. Как правило,
ha<<2a, а поэтому, учитывая малость ha2, можно считать:
rm2≈2a.ha или ha≈rm2/2a. Аналогично можно получить для
ΔBAP: rm2 = (b + mλ/2)2 – (b + mλ/2 – hb)2 = (2b + mλ – hb)hb,
и пренебрегая слагаемыми с mλ
A
bm= b+mλ/2 и h 2 по сравнению с 2b, имеем
b
a
hb≈rm2/2b. Подставив выражеS0
P ния для ha и hb в их сумму,
C
O b
получаем rm2(1/2a +1/2b) =
ha
hb B
mλ/2.
Таким образом для падающей сферической волны имеем:
(10)
r m ab (a b)
m

10. Метод зон Френеля. Векторная диаграмма

• Расчет размеров зон Френеля
В случае нормального падения на отверстие плоской
волны (для нее а ∞) имеем:
rm m b
(11)
Определим площадь m-ой зоны Френеля ΔSm. Для этого
найдем
разность
боковых
поверхностей
сферических
сегментов с основаниями Øm= 2rm и Øm-1= 2rm-1, используя
известную формулу для такой поверхности S = 2 .a.ha:
ΔSm = Sm – Sm-1 ≈ λ.ab /(a + b)
(12)
Как видно, все зоны Френеля – равновелики (их поверхности
не зависят от номера m).

11. Метод зон Френеля. Векторная диаграмма

• Расчет дифракции от круглого отверстия
Фазы колебаний, возбуждаемых в (.) Р соседними зонами
Френеля, отличаются на π (т.е. находятся в противофазе),
поэтому амплитуда результирующего колебания может быть
представлена в виде алгебраической суммы амплитуд,
обусловленных действием соответствующих зон Френеля:
АР = А1 – А2 + А3 – А4 + … ± Аm
(5)
Причем для зон Френеля выполняется неравенство:
А1> А2 > А3 > … Аm – 1 > Am , так как расстояние bm от зоны до
(.) Р монотонно растет с номером m и угол φ также растет, а
коэффициент К(φ) в уравнении (1) – быстро уменьшается.
Вывод. Результирующая амплитуда (и интенсивность) зависит
от того, четное или нечетное число m зон Френеля умещается
в отверстии для точки наблюдения Р: - если m нечетное, то
получаем Imax, – если m четное, то получаем Imin.
Таким образом можно представить рекурентную формулу:
АР = А1/2 ± Аm/2
(5′)

12. Метод зон Френеля. Векторная диаграмма

• Расчет дифракции от круглого отверстия
Если представить случай полностью открытого волнового
фронта, то имеем:
АР = А1/2 + (А1/2 – А2 + А3/2) + (А3/2 – А4 + А5/2) + …
+ (Аm-1/2 – Аm + Am+1/2)
(6)
а с учетом, что Am-1/2 + Am+1/2 = Am, как среднее значение, то
все выражения в скобках в (6) равны нулю и, следовательно,
АР = А∞ ≈ А1/2
(7)
Таким образом, амплитуда в (.)Р, создаваемая всей
сферической волновой поверхностью (или бесконечным
числом открытых зон Френеля), равна половине амплитуды от
1-ой зоны Френеля.
• Векторная диаграмма
Векторная диаграмма является наглядной графической
иллюстрацией метода зон Френеля. В этом случае каждую
зону разбивают на огромное число N элементарных
кольцевых подзон. Амплитуду колебаний, создаваемых
каждой подзоной, изображают в виде элементарного
амплитуд-вектора dA.

13. Метод зон Френеля. Векторная диаграмма

• Векторная диаграмма
Вследствие увеличения расстояния r и уменьшения коэффициента К(φ) амплитуда колебаний от каждой следующей
подзоны будет чуть-чуть меньше по модулю и отставать по
фазе на dδ от колебаний предыдущей подзоны. Откладывая
из (.) О некоторой горизонтальной базы последовательно все
N амплитуд-векторов dAi с соответствующим поворотом на
угол dδ против часовой стрелки, можно получить векторную
цепочку, которая определяет действие всей открытой 1-ой
зоны Френеля. Замыкающий эту цепочку вектор А1 есть
амплитуд-вектор полностью открытой 1-ой зоны Френеля.
δ=π
δ = 2π
dAN
А1
О
δ = 3π
Спираль Френеля
А3
dδ
A2 0 О
A∞≈ А1/2 О
О
dA1
Открыта вся
Открыта 1-я Открыты две первые Открыты три первые
волновая
зоны Френеля
зоны Френеля
зона Френеля
поверхность

14. Метод зон Френеля. Векторная диаграмма

• Векторная диаграмма
Таким образом, по мере увеличения радиуса отверстия в
преграде амплитуда колебаний (и интенсивность света) в (.) Р
изменяется не монотонно при переходе от одной зоны
Френеля к другой. Монотонное изменение амплитуды
происходит только в пределах одной наблюдаемой зоны.
Замечание. Аналогичную динамику изменения освещенности экрана
можно наблюдать, если вместо увеличения отверстия – приближать к
нему экран с точкой наблюдения Р.
Выводы. Наибольшая освещенность в центре экрана
наблюдается при полностью открытой 1-ой зоне Френеля (I1).
Так как интенсивность света I пропорциональна А2, то
интенсивность в (.) Р при полностью открытой волновой
поверхности (А∞ = А1/2) в 4 раза меньше, чем при открытой
только 1-ой зоне Френеля, т.е. I∞ = I1/4. При полностью
открытых первых двух зонах результирующая амплитуда А2
0 и, следовательно, I2 0, хотя световой поток через
отверстие – вдвое больше.
Замечание. Если отверстие открывает лишь часть 1-ой
Френеля, то на экране получается размытое светлое пятно.
зоны

15. Дифракция Френеля от круглого отверстия (и от круглого диска)

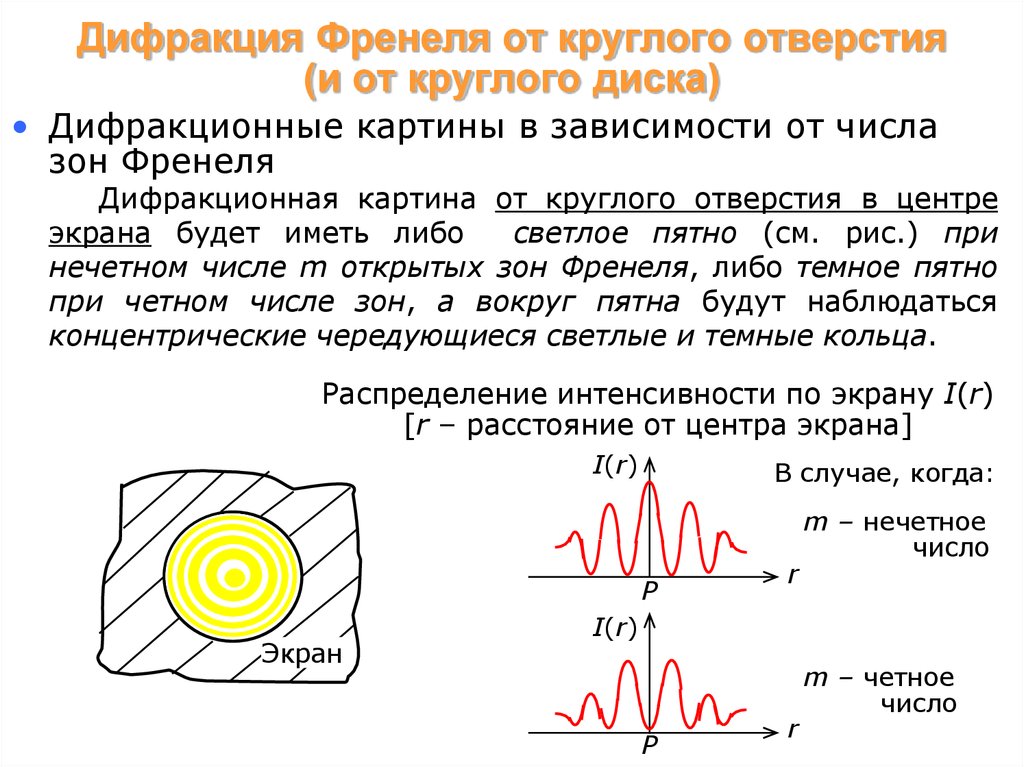
• Дифракционные картины в зависимости от числа
зон Френеля
Дифракционная картина от круглого отверстия в центре
экрана будет иметь либо
светлое пятно (см. рис.) при
нечетном числе m открытых зон Френеля, либо темное пятно
при четном числе зон, а вокруг пятна будут наблюдаться
концентрические чередующиеся светлые и темные кольца.
Распределение интенсивности по экрану I(r)
[r – расстояние от центра экрана]
I(r)
В случае, когда:
P
Экран
r
m – нечетное
число
I(r)
P
r
m – четное
число

16.

17. Дифракция Френеля от круглого отверстия (и от круглого диска)

• Дифракция Френеля от круглого (малого) диска
I(r)
O
r
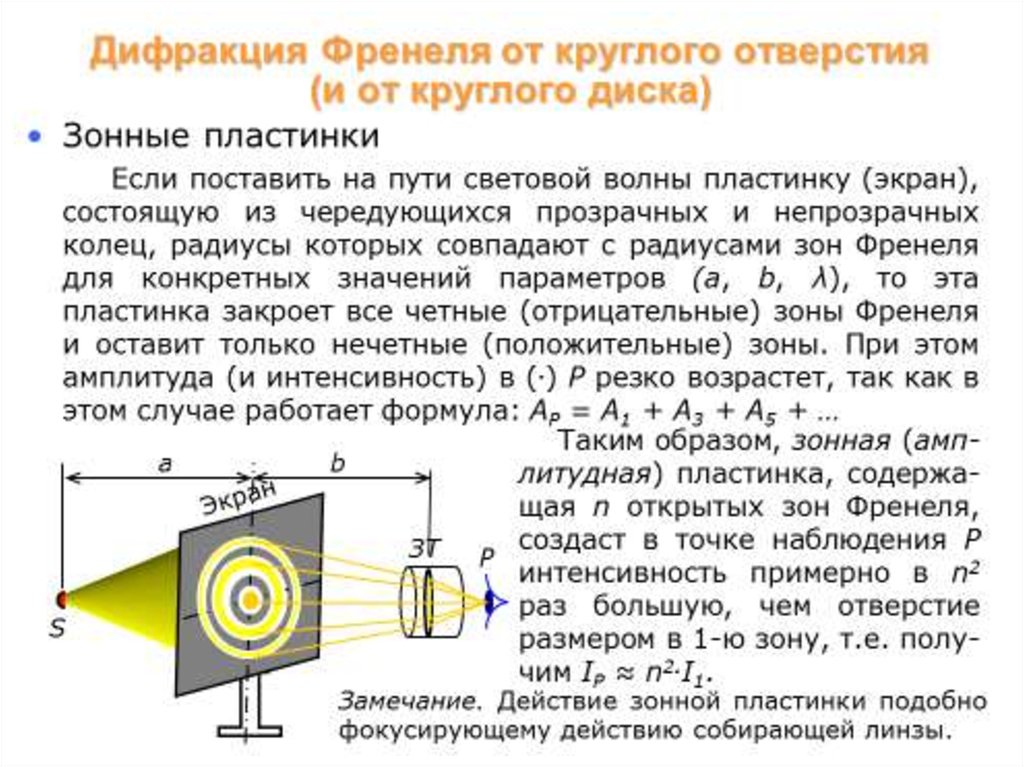
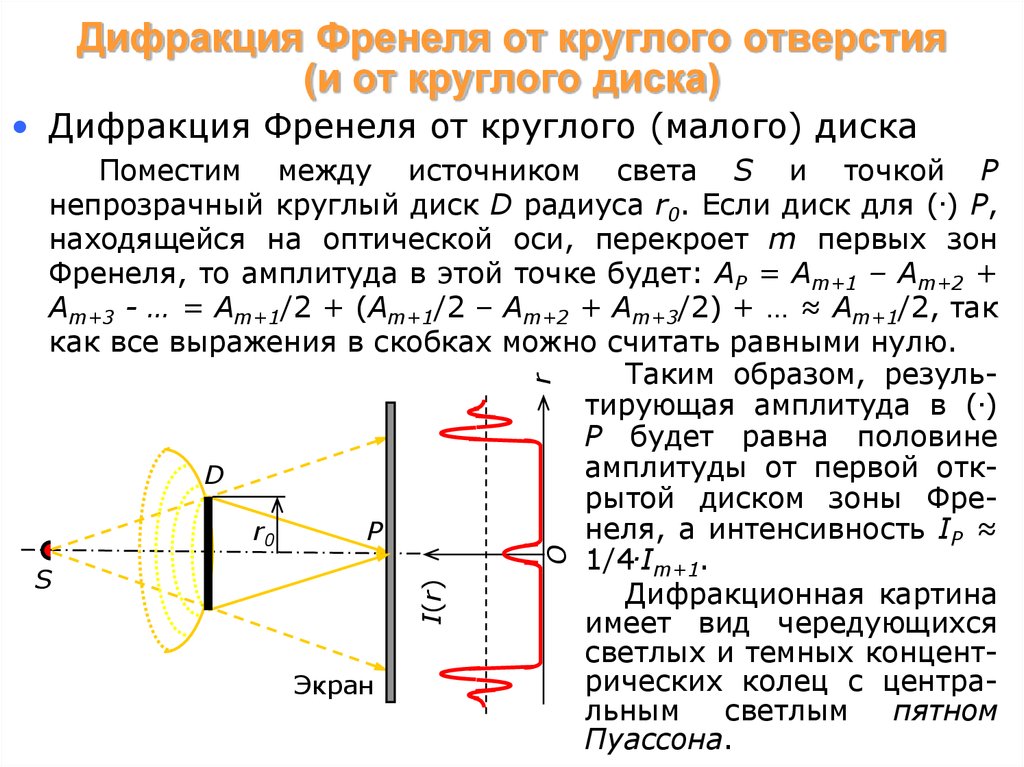
Поместим между источником света S и точкой Р
непрозрачный круглый диск D радиуса r0. Если диск для (.) Р,
находящейся на оптической оси, перекроет m первых зон
Френеля, то амплитуда в этой точке будет: АР = Аm+1 – Аm+2 +
Аm+3 - … = Am+1/2 + (Am+1/2 – Am+2 + Am+3/2) + … ≈ Am+1/2, так
как все выражения в скобках можно считать равными нулю.
Таким образом, результирующая амплитуда в (.)
Р будет равна половине
амплитуды от первой откD
рытой диском зоны Френеля, а интенсивность IP ≈
r0
P
1/4.Im+1.
S
Дифракционная картина
имеет вид чередующихся
светлых и темных концентрических колец с центраЭкран
льным
светлым
пятном
Пуассона.

18. Дифракция Фраунгофера от щели

Пусть на бесконечную прямую щель Sh ширины b падает
нормально плоская световая волна с длиной λ. Поместим за
щелью собирающую линзу, а в ее фокальной плоскости экран.
Разобьем мысленно щель (т.е. открытую часть волнового
фронта) на очень узкие, одинаковые по ширине, зоны –
полоски, параллельные прямолинейным краям щели. Суммирование вторичных волн проведем с помощью векторной диаграммы. Колебания, приходящие в (.) Р от каждой такой полоски имеют одинаковую амплитуду dA
λ
поскольку распространяются паралSh
лельно друг другу перед линзой;
при этом разность фаз dδ между
.
∆ = b sinφ колебаниями от соседних полосок
φ b
будет постоянной.
O
Линза
Таким образом при графическом
f
построении получим цепочку вектоP P0
Экран
ров dAi, одинаковых по модулю и
повернутых относительно друг друга
на один и тот же угол dδ, который зависит от угла дифракции φ.

19. Дифракция Фраунгофера от щели

• Условие дифракционных минимумов
Результирующую амплитуду – вектор А (см. рис. 1) можно
рассматривать как хорду дуги окружности с центром в (.) С и
радиуса R.
Для центральной точки Р0, т.е. при угле дифракции = 0,
разность фаз = 0 и векторная диаграмма превращается в
прямую цепочку, что соответствует центральному (m = 0)
максимуму I0, который пропорционален А02(см. рис. 2).
dAN
R=A0/
С
|А|= А0
dA1
D=A0/
dAN Рис. 2
Рис. 3
А
В случае, когда оптическая
.
А0=R
разность хода Δ, выражаемая как
b.sin , равна длине волны λ, то
dδ
О
колебания, исходящие от краев
dA1
Рис. 1
щели, отличаются по фазе на = 2 ,
и цепочка векторов оказывается замкнутой на себя (рис. 3), а
амплитуда результирующего колебания А обращается в 0. Это
первый минимум дифракционной картины, т.е. симметричной
относительно (.) Р0 системы чередующихся светлых и темных
полос.

20. Дифракция Фраунгофера от щели

• Условие дифракционных минимумов
Результирующая амплитуда обращается в нуль также при
= m.2 , где m =1, 2, 3,… ( = 2 /λ.Δ). Цепочка элементарных
векторов замыкается после m-оборотов, практически не
меняя своей длины А0.
Таким образом, условие наблюдаемых на экране
минимумов интенсивности Imin:
b.sin m = ±m.λ
(8)
• Условие (дополнительных) максимумов
b.sin m = ±(2m+1)λ/2
(9)
при этом разность фаз составляет = (2m+1) .
Так
первый
дополнительный
максимум возникает при условии Δ
= b.sin = 3λ/2, в этом случае
А1=2/3 .А0
колебания, исходящие от противоположных краев щели, отличаются
по фазе на = 3 . Диаметр полученной после полуторного
обхода окружности есть амплитуда этого максимума А1=2/3 ..А0
Таким образом получаем I1= (2/3 )2.I0 ≈ 0,045.I0.

21. Дифракция Фраунгофера от щели

Для других максимумов получается соотношение:
I0: I1: I2: I3:…=1:(2/3 )2:(2/5 )2:(2/7 )2:…≈
≈1: 0,045: 0,016: 0,008:…
• Закон распределения интенсивности
Из рис. 1 имеем A = 2R.sin( /2), а так как R = A0/ , то
получаем A = A0.sin( /2)/( /2). Тогда с учетом, что I ~ A2,
запишем для интенсивности:
I = I0.sin2 / 2
(10)
где = /2 = /λ.Δ = /λ.b.sin .
Таким образом интенсивность зависит от угла дифракции
Количество
минимумов
определяется
соотношением
ширины щели b к длине волны падающего света λ; так как
sin = ±mλ/b, а |sin | ≤ 1, то получаем неравенство mλ/b ≤
1 или для возможных m ≤ b/λ.
В случае b < λ минимумы вообще не возникают; здесь
освещенность от центра монотонно убывает к краям картины.

22. Дифракция Фраунгофера от щели

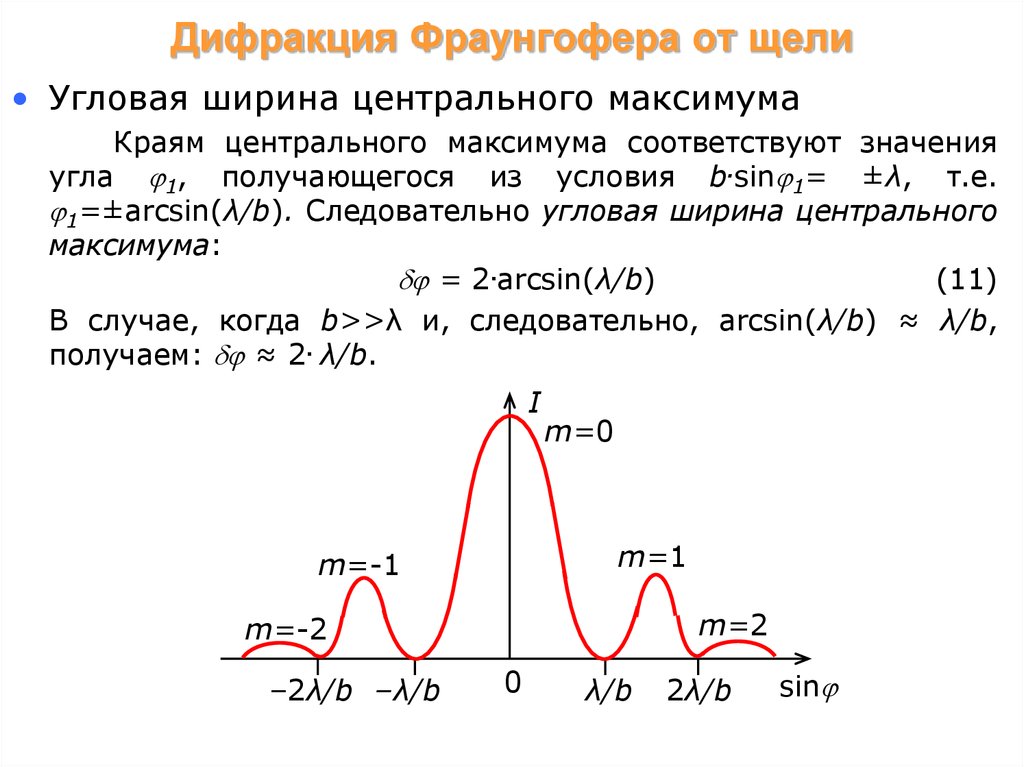
• Угловая ширина центрального максимума
Краям центрального максимума соответствуют значения
угла 1, получающегося из условия b.sin 1= ±λ, т.е.
1=±arcsin(λ/b). Следовательно угловая ширина центрального
максимума:
= 2.arcsin(λ/b)
(11)
В случае, когда b>>λ и, следовательно, arcsin(λ/b) ≈ λ/b,
получаем: ≈ 2. λ/b.
I
m=0
m=1
m=-1
m=2
m=-2
–2λ/b –λ/b
0
λ/b
2λ/b
sin

23. Предельный переход от волновой оптики к геометрической

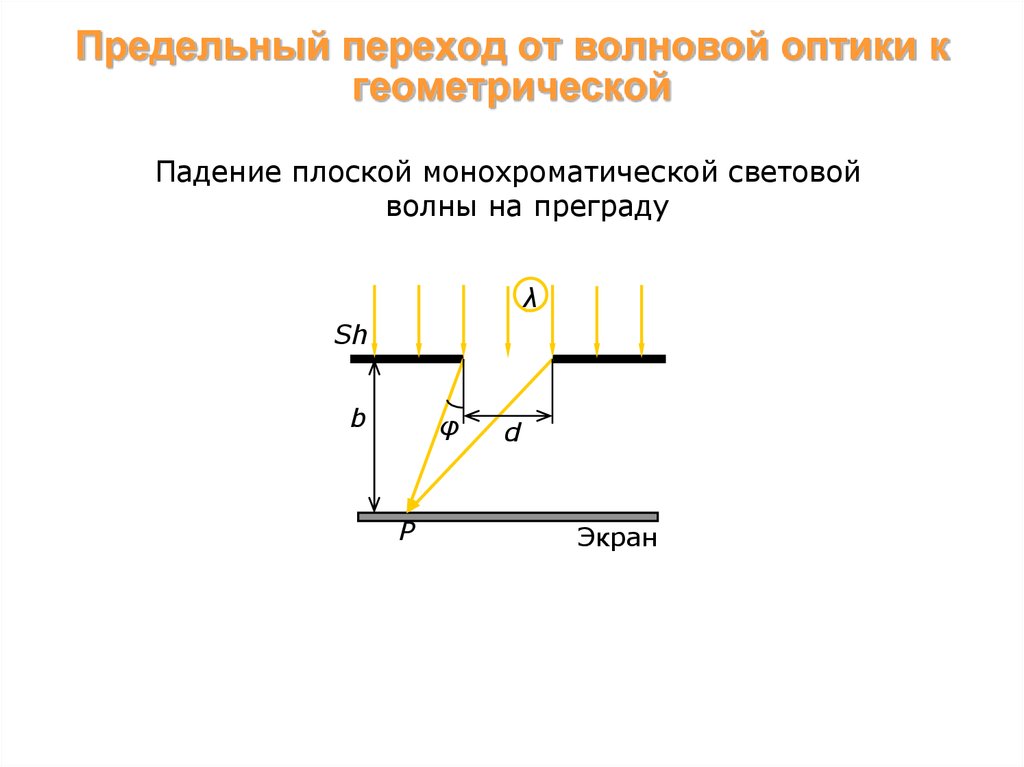
24. Предельный переход от волновой оптики к геометрической

Падение плоской монохроматической световой
волны на преграду
λ
Sh
b
φ
P
d
Экран