Решение показательных уравнений

1. МКОУ «Горшеченская СОШ им. Н.И. Жиронкина»

Математика
МКОУ «Горшеченская СОШ им. Н.И. Жиронкина»
Решение показательных
уравнений

2.

Расскажи – и я забуду,
Покажи – и я запомню,
Дай мне сделать самому – и я научусь!
Китайская мудрость

3.

Вычислите
1) 64
2)1
3) 1/64
4) 1/81
1) 2 6
2) 7 0
3) 4 3
4)3 4
1
5)
5
6)8
5) 125
6) 4
2
3
7)81
3
3
4
8) 2 5
7)27
8) 1/32

4.

Определение
Уравнение, в котором переменная
содержится в показателе степени,
называется показательным.
Примеры:
5х=1
49x+0,5 • 7x-2 =1
2-х=30,5х
3х + 33-х = 12

5.

Простейшим показательным уравнением
является уравнение вида
a a , где a 0, a 1.
x
b
Простейшее показательное уравнение
решается с использованием свойств
степени .
a a x b
x
b

6.

7.

Решите уравнения
1)3 х 27
1) х=3
2) 2 х 128
1
3) 2 х
8
4) 4 х 64
2)х=7
х
1
1
5)
625
5
1
6) 7 х
343
3) х= -3
4) нет решений
5) х=4
6) х= -3
х
1
7) 0
9
7)нет решений
х
1
8) 36
6
8) х= -2

8. Математический диктант «Крестики-нолики»

1
2
3
4
5
6
7
8
9
ДА – Х, НЕТ – О
Вопросы:
1) Область определения показательной функции – множество всех
действительных чисел?
2) При умножении степеней с одинаковым основанием – показатели
умножают?
3) Показательная функция с основанием а>1 является возрастающей?
4) При возведении степени в степень показатели складывают?
5) Любое действительное число в нулевой степени равно 1?
6) Область значений показательной функции – множество всех
действительных чисел?
7) Показательная функция с основанием 0<а<1 является убывающей?
х
8) Х=0 – корень уравнения 7 0
х
9) Не имеет корней уравнение 15 15

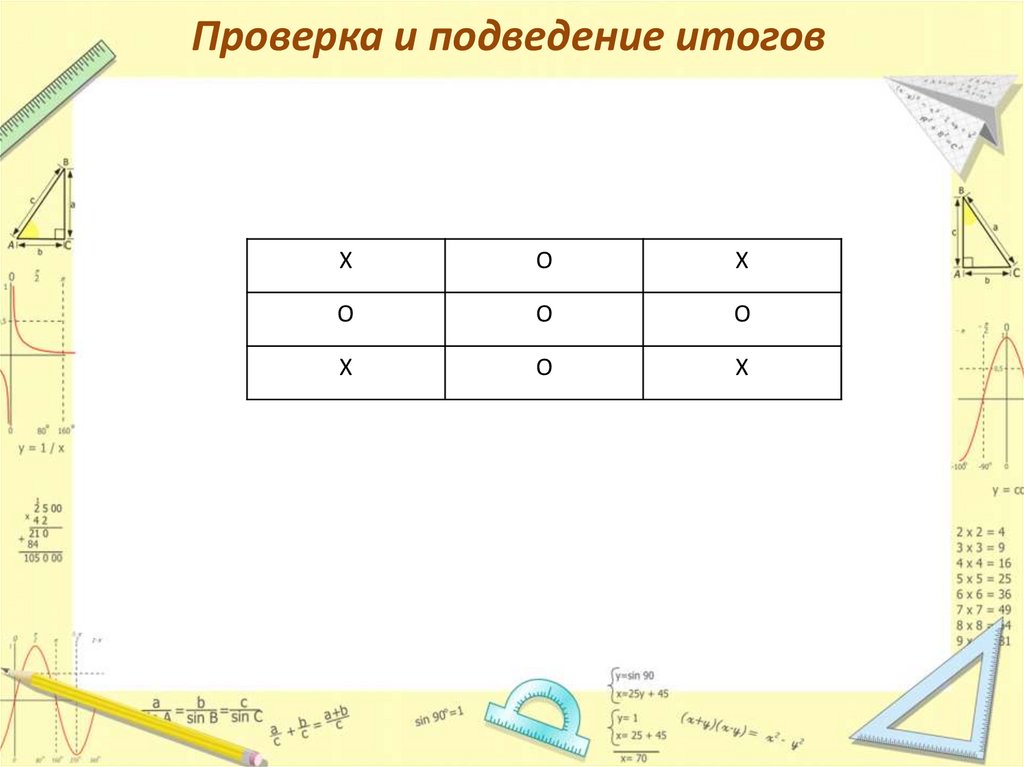
9. Проверка и подведение итогов

Х
О
Х
О
О
О
Х
О
Х

10. Метод замены переменной

Показательное уравнение сводится к решению
квадратного.
Способы замены используют, если:
1) основания степеней одинаковы;
2) показатель одной из степеней в 2 раза
больше, чем другой. Например: 9х - 8·3х = 9;
3) коэффициенты перед переменной
2-х
х–1
противоположны. Например: 2
–2
=1.

11.

Решим уравнения
9х - 8·3х = 9
32 x 8 3 x 9 0
3 x t , (t 0)
t2 8 t 9 0
D 64 36 100
8 10
t
9
1
2
8 10
t
1,
2
2
3х 9
3 х 32
x 2
Ответ : x 2
2 2 - х – 2 х – 1 =1
2 2 2 x 2 x 2 1 1
2x
4
1 0
2
2x
2 x t , (t 0)
t
4
1 0 / 2t
2
t
t 2 2t 8 0
D 4 32 36
2 6
2
t1
2
2 6
4
t2
2
2x 2
x 1
Ответ : х 1

12.

Решить самостоятельно:
1 вариант
2 вариант
14 7 х 7 х 5 0
3 х 1 2 3 х 1 0

13. Метод вынесения наименьшего общего множителя за скобки.

Этот метод используется, если
соблюдаются два условия:
основания степеней одинаковые;
коэффициенты перед переменной
одинаковые.
Например: 2 x 1 4 2 x 2 32

14.

Решим уравнения:
2 x 1 1 2 2 12
2 x 1 3 12
5 x 2 3 5 200
5 x 2 8 200
2 x 1 4
5 x 2 25
2 x 1 2 2
x 1 2
x 1
Ответ : x 1
5 x 2 52
x 2 2
x 4
Ответ : x 4

15.

Примеры:

16. Деление на показательную функцию

Этот способ используется, если основания
степеней разные:
x
x
x
a) в уравнении вида a = b делим на b
х
х
x
Например: 4 = 7 | : 7
2x
x
2x
b) в уравнении A a + B (ab) + C b = 0
2x
делим на b .
Например:
х
х
х
x
3 25 - 8 15 + 5 9 = 0 | : 9

17.

Решим уравнения:
3 25 х 8 15 х 5 9 х 0 : 9
D 64 4 3 5 4 2 2
25 х
15 x
3 х 8 x 5 0 t1 8 2 10 5 ; t 8 2 1.
2
6
6 3
9
9
6
х
2x
x
5
5
3 8 5 0
3
3
5
t
3
х
(t 0)
3t 8t 5 0
х
5
5
3
3
5
1
3
х 1
5 5
3 3
х
х
х 0
2
Ответ: 0; 1
0

18.

Пример:

19. Графический метод

Метод основан на использовании графических иллюстраций, или
каких-либо свойств функций.
• Решите уравнение 4 х 5 х
Построим в одной системе координат графики функций
у 4х
х
у
-2
1/16
-1
1/4
0
1
1
4
2
16
и у = 5 - х.
х
0
1
у
5
4
Графики пересекаются в одной точке (1; 4).
х=1 – решение уравнения.
Ответ: 1.

20.

Решите графически уравнение
3х 4 х

21. Домашнее задание

№ 468 (в,г)
№ 470 (в,г)
стр. 299 № 166 (а,г)

22.

Спасибо за Внимание!