Понятие энергии, работы и мощности. Лекция 4

1. Понятие энергии, работы и мощности

Лекция 4
Понятие энергии, работы и мощности
1

2.

Пример: Пусть тело массой m падает с высоты 20 м
на сваю и тело массой 2m с высоты 5 м на другую
сваю. Определить импульсы двух тел.
Еп Ек
m
mgh
2
2
2gh
p1 m m 2gh1 20m
p2 m 2m 2gh 2 20m
2

3.

Энергия – универсальная мера различных форм
движения и взаимодействия.
Количественная мера энергии т.е количественная
характеристика процесса обмена энергией между
взаимодействующими телами - работа.
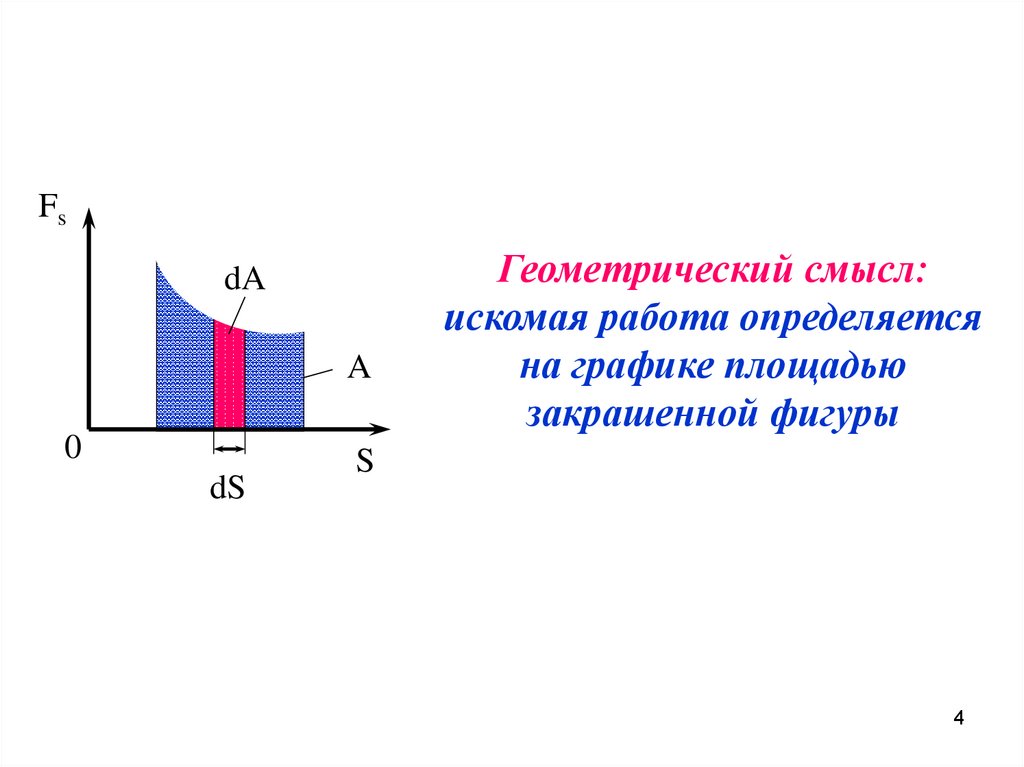
F
Fs
dА Fs dS FdScos
s
А FdScos
0
const
F const
s
A Fcos ds FScos
0
3

4.

Fs
dA
A
0
dS
Геометрический смысл:
искомая работа определяется
на графике площадью
закрашенной фигуры
S
4

5.

Если F=0, то А=0;
Если S=0, то А=0;
Если < π/2 работа силы положительна, в этом
случае
составляющая
Fs
совпадает
по
направлению с вектором скорости движения ;
Если > π/2, то работа силы отрицательна;
Если =π/2 (сила направлена перпендикулярно
перемещению) А=0.
5

6.

Пример:
Некоторая
точка
вращается
по
окружности.
На
нее
действует
центростремительная сила. Определить работу
этой силы.
A FScos
Fц
Fy
K
r
работа не совершается т.к.
Fц и
2
6

7.

Мощность - скорость совершения работы.
dA
N
dt
Fdr
N
F
dt
Мощность равна скалярному произведению
вектора силы на вектор скорости, с которой
движется точка приложения этой силы
7

8. Кинетическая и потенциальная энергии

8

9.

Механическая
энергия
кинетическая
потенциальная
9

10.

Кинетическая энергия механической системы –
это энергия механического движения этой
системы.
dA dЕ к
d
F m
dt
dr
т.к.
dt
то dA m d m d dE к
d
Fdr=m dr dA
dt
m 2
E к m d
2
0
Кинетическая энергия зависит от выбора системы отсчета.
10

11.

Потенциальная энергия – механическая энергия
системы тел, определяемая их взаимным
расположением и характером сил взаимодействия
между ними.
1
2
Поля называются потенциальными, а силы,
действующие в них, – консервативными если работа,
совершаемая
действующими
силами
при
перемещении тела из одного положения в другое, не
зависит от того, по какой траектории это
перемещение произошло, а зависит только от
11
начального и конечного положений.

12.

Если же работа, совершаемая силой, зависит от
траектории перемещения тела из одной точки в
другую,
то
такая
сила
называется
диссипативной; ее примером является сила
трения.
dA –dЕ п ;
т.к. dА Fdr,
то Fdr –dЕ п
Е п Fdr С
12

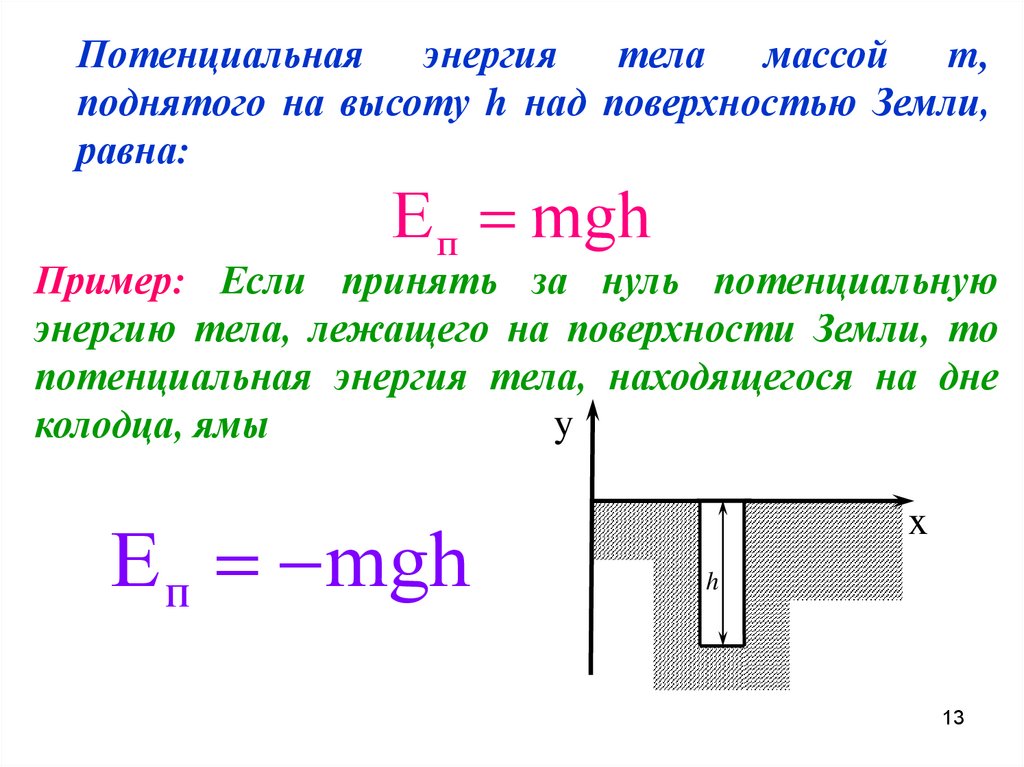
13.

Потенциальная энергия тела массой m,
поднятого на высоту h над поверхностью Земли,
равна:
Е п mgh
Пример: Если принять за нуль потенциальную
энергию тела, лежащего на поверхности Земли, то
потенциальная энергия тела, находящегося на дне
y
колодца, ямы
Е п mgh
x
h
13

14.

Потенциальная энергия упругодеформированного
тела (пружины).
Fx упр kx
Fx Fx упр =kx
dA Fx dx kxdx
x
kx
A kxdx
2
0
kx
Еп
2
2
2
14

15.

Потенциальная энергия системы является
функцией состояния системы. Она зависит
только от конфигурации системы и ее положения
по отношению к внешним телам.
Полная механическая энергия системы – энергия
механического движения и взаимодействия равна
сумме кинетической и потенциальной энергий.
Е Ек Еп
15

16. Закон сохранения энергии

16

17.

E A внеш
Aвнеш 0
E 0
Е const
Выражение представляет собой закон сохранения
механической энергии в системе тел, между
которыми действуют только консервативные
силы, полная механическая энергия сохраняется,
т. е. не изменяется со временем.
17

18.

Механические системы, на тела которых
действуют
только
консервативные
силы
(внутренние
и
внешние),
называются
консервативными системами.
Закон сохранения механической энергии можно
сформулировать так: в консервативных системах
полная механическая энергия сохраняется.
18

19.

Закон
сохранения
механической
энергии
фундаментальный закон природы, он справедлив
как для систем макроскопических, тел, так и для
систем микротел и связан с однородностью
времени.
Существует
еще
одни
вид
систем
–
диссипативные системы, в которых механическая
энергия постепенно уменьшается за счет
преобразования в другие (немеханические) формы
энергии. Этот процесс получил название
диссипации (или рассеяния) энергии.
19

20.

Энергия никогда не исчезает и не появляется
вновь, она лишь превращается из одного вида в
другой.
В этом и заключается физическая сущность
закона сохранения и превращения энергии –
сущность неуничтожимости материи и ее
движения.
20

21. Абсолютно упругий и неупругий удар

21

22.

Удар (или соударение) – это столкновение двух
или более тел, при котором взаимодействие
длится очень короткое время.
22

23.

Абсолютно упругий удар – столкновение двух тел,
в
результате
которого
в
обоих
взаимодействующих телах не остается никаких
деформаций и вся кинетическая энергия, которой
обладали тела до удара, после удара снова
превращается в кинетическую энергию.
Выполняются: закон сохранения импульса и закон
сохранения механической (кинетической) энергии.
m1 1 m2 2 mU
1 1 m2U 2
m
m
m1U
m2U
2
2
2
2
2
1 1
2
2 2
2
1
2
2
23

24.

Абсолютно неупругий удар – столкновение двух
тел, в результате которого тела объединяются,
двигаясь дальше как единое целое.
Выполняется: закон сохранения импульса
Не выполняется: закон сохранения механической
энергии.
24