Similar presentations:
Rotation and translation. Year 9
1.
Rotation and translationYear 9
#MathsEveryoneCan
2.
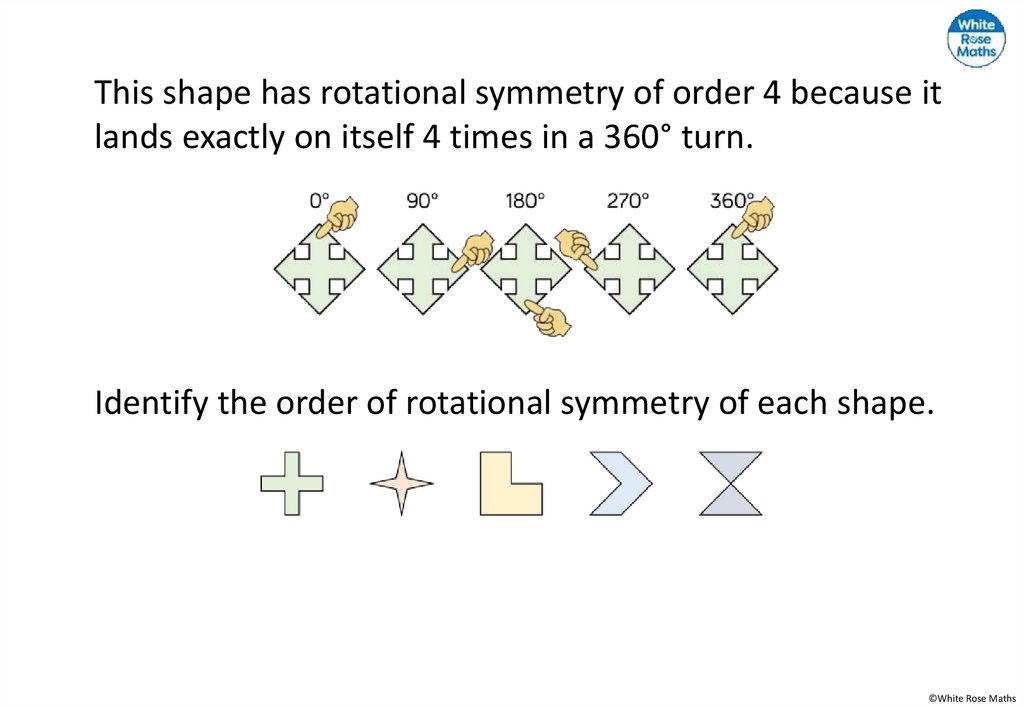
This shape has rotational symmetry of order 4 because itlands exactly on itself 4 times in a 360° turn.
Identify the order of rotational symmetry of each shape.
©White Rose Maths
3.
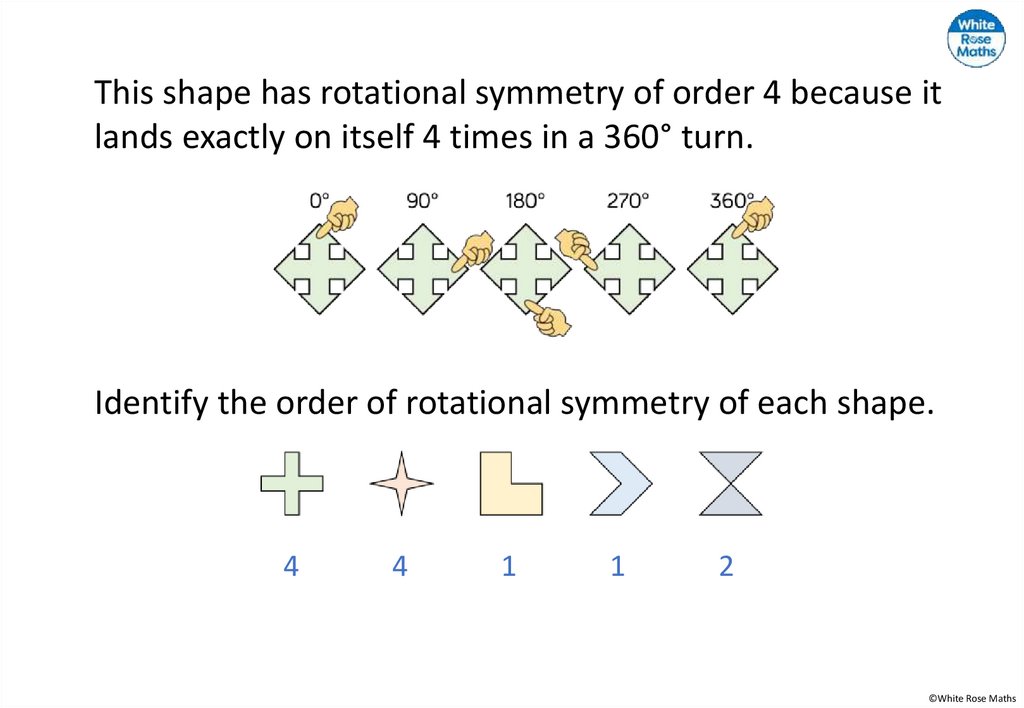
This shape has rotational symmetry of order 4 because itlands exactly on itself 4 times in a 360° turn.
Identify the order of rotational symmetry of each shape.
4
4
1
1
2
©White Rose Maths
4.
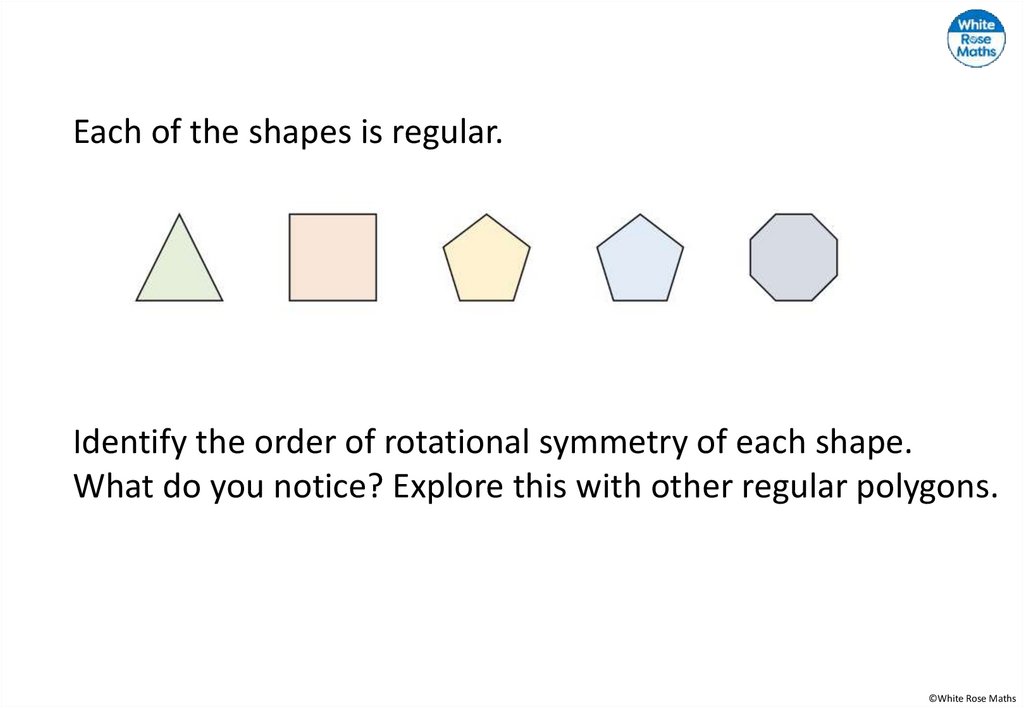
Each of the shapes is regular.Identify the order of rotational symmetry of each shape.
What do you notice? Explore this with other regular polygons.
©White Rose Maths
5.
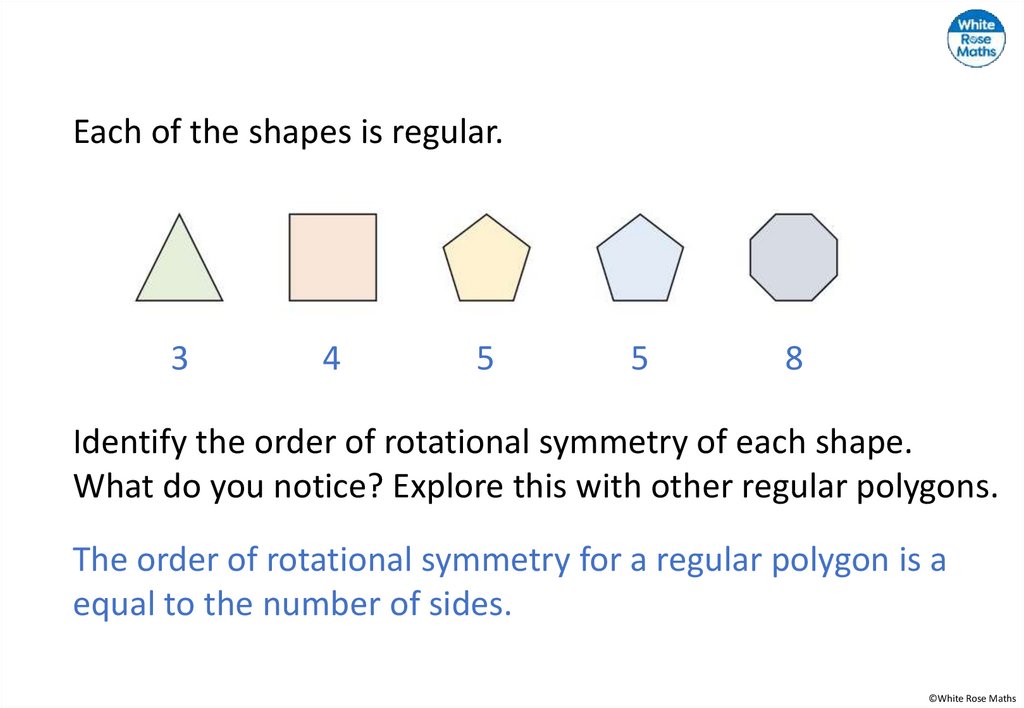
Each of the shapes is regular.3
4
5
5
8
Identify the order of rotational symmetry of each shape.
What do you notice? Explore this with other regular polygons.
The order of rotational symmetry for a regular polygon is a
equal to the number of sides.
©White Rose Maths
6.
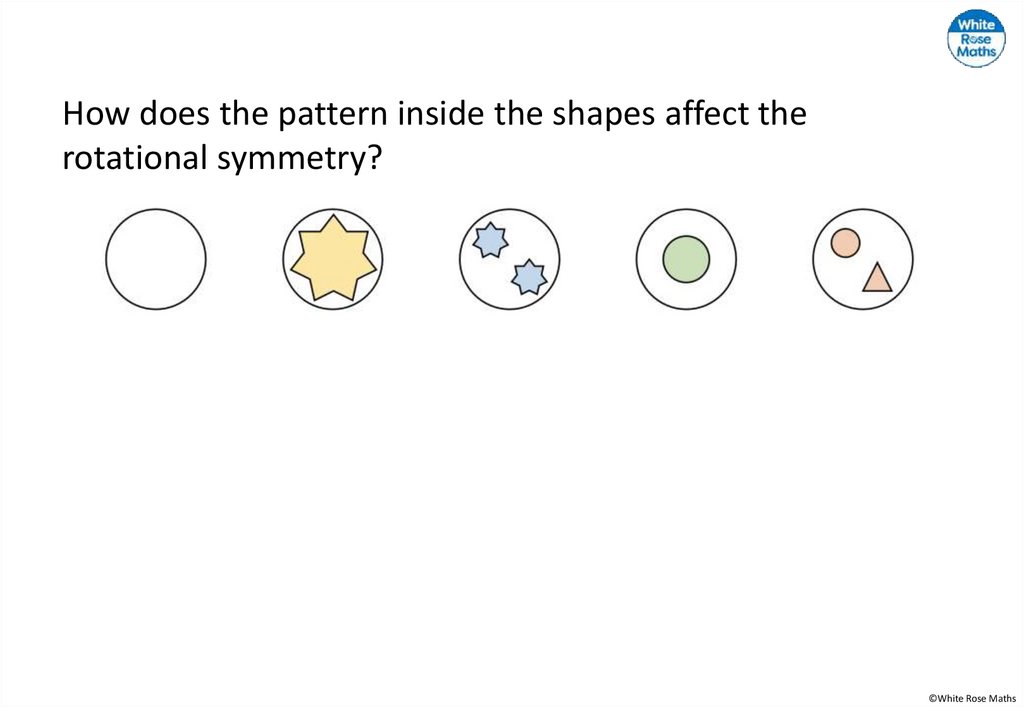
How does the pattern inside the shapes affect therotational symmetry?
©White Rose Maths
7.
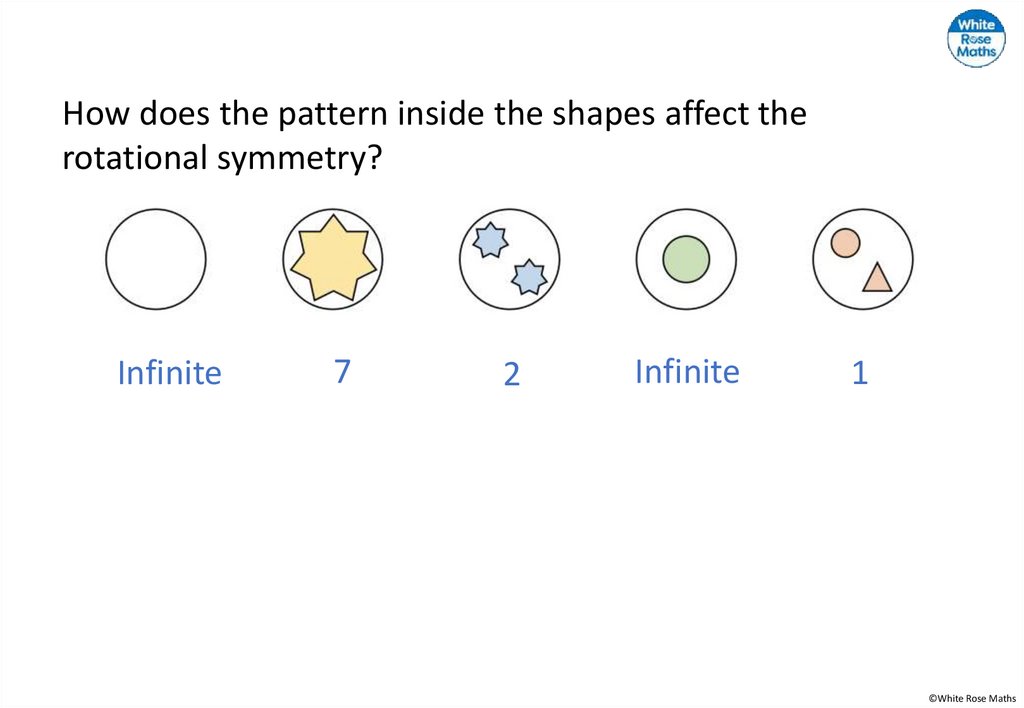
How does the pattern inside the shapes affect therotational symmetry?
Infinite
7
2
Infinite
1
©White Rose Maths
8.
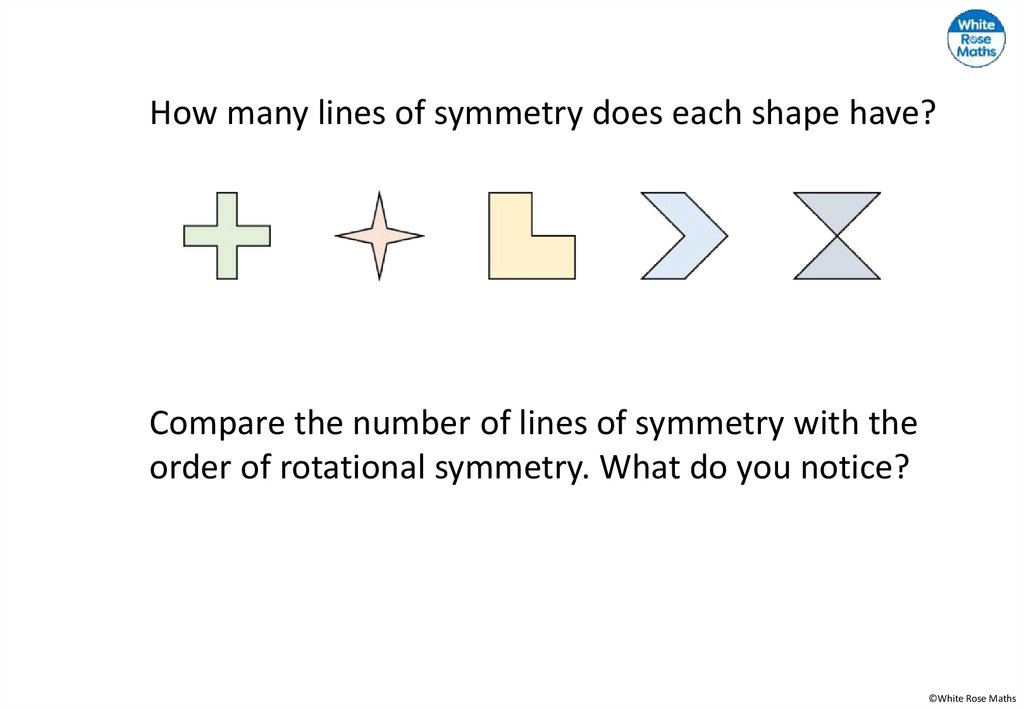
How many lines of symmetry does each shape have?Compare the number of lines of symmetry with the
order of rotational symmetry. What do you notice?
©White Rose Maths
9.
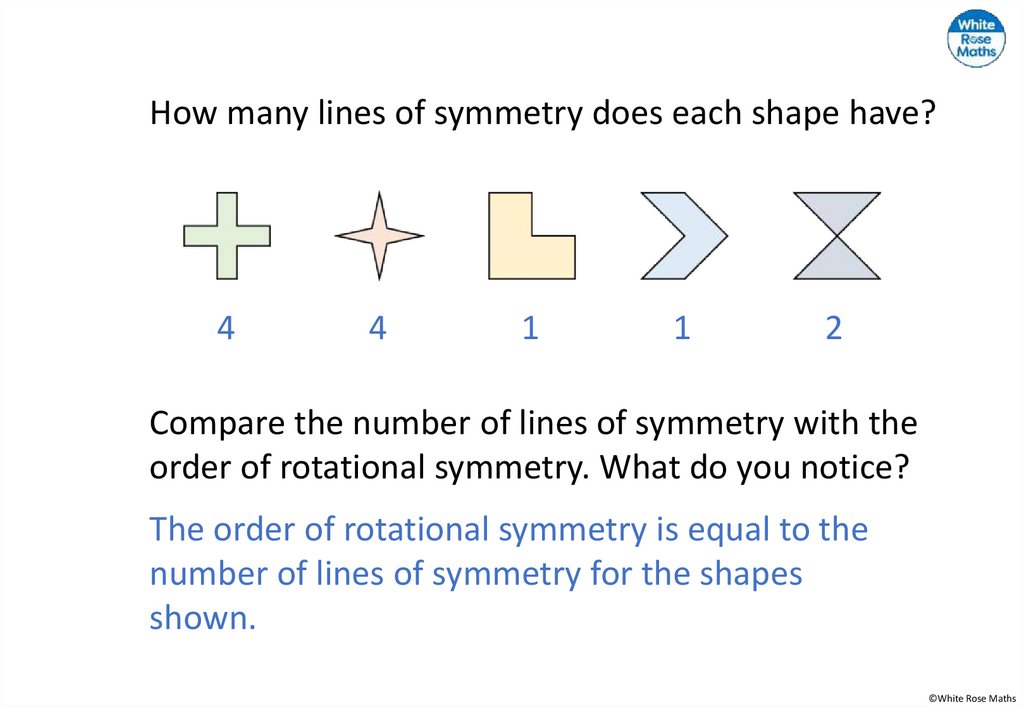
How many lines of symmetry does each shape have?4
4
1
1
2
Compare the number of lines of symmetry with the
order of rotational symmetry. What do you notice?
The order of rotational symmetry is equal to the
number of lines of symmetry for the shapes
shown.
©White Rose Maths
10.
Decide whether each statement is always, sometimes or never true.Explain your reasoning, including examples where appropriate.
The more lines of symmetry a shape has, the greater its order of
rotational symmetry.
The order of rotational symmetry of a shape is equal to the
number of lines of symmetry.
If a shape has line symmetry then it has rotational symmetry of
order greater than 1
©White Rose Maths
11.
Decide whether each statement is always, sometimes or never true.Explain your reasoning, including examples where appropriate.
The more lines of symmetry a shape has, the greater its order of
rotational symmetry. True
The order of rotational symmetry of a shape is equal to the
number of lines of symmetry. Sometimes true
If a shape has line symmetry then it has rotational symmetry of
order greater than 1 Sometimes true
Discuss examples as a class.
©White Rose Maths
12.
The interior angles of a regular polygon is 156°How many sides does the polygon have?
How many lines of symmetry does the polygon have?
Identify the order of rotational symmetry of the
polygon.
©White Rose Maths
13.
The interior angles of a regular polygon is 156°How many sides does the polygon have?
15 sides
How many lines of symmetry does the polygon have?
15 lines of symmetry
Identify the order of rotational symmetry of the
polygon.
Order of rotational symmetry is 15
©White Rose Maths
14.
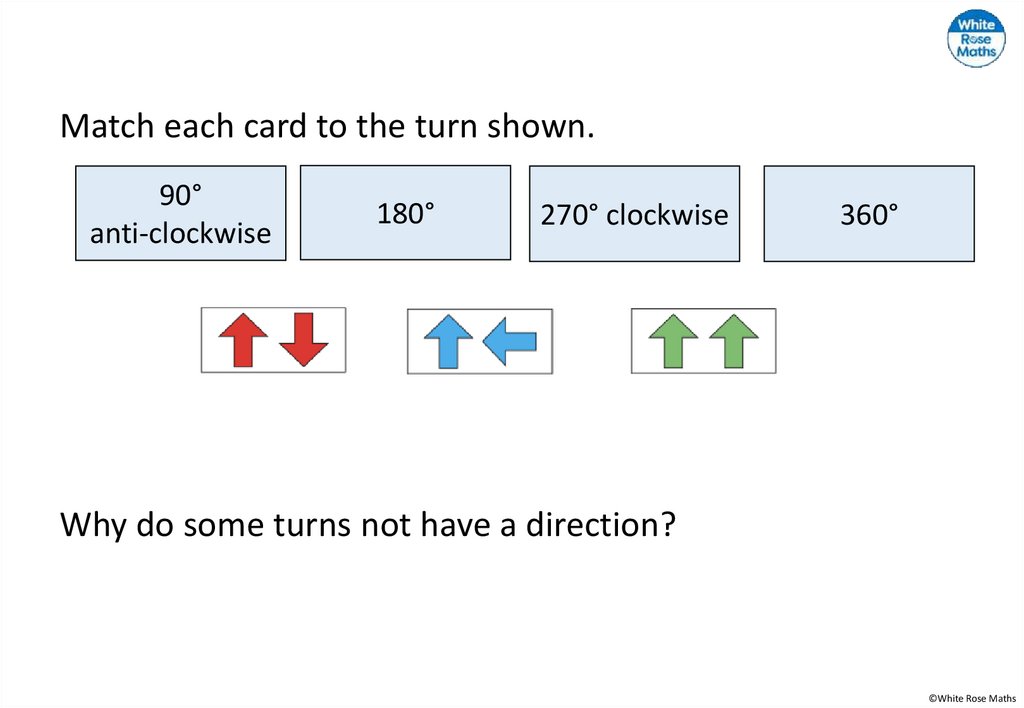
Match each card to the turn shown.90°
anti-clockwise
180°
270° clockwise
360°
Why do some turns not have a direction?
©White Rose Maths
15.
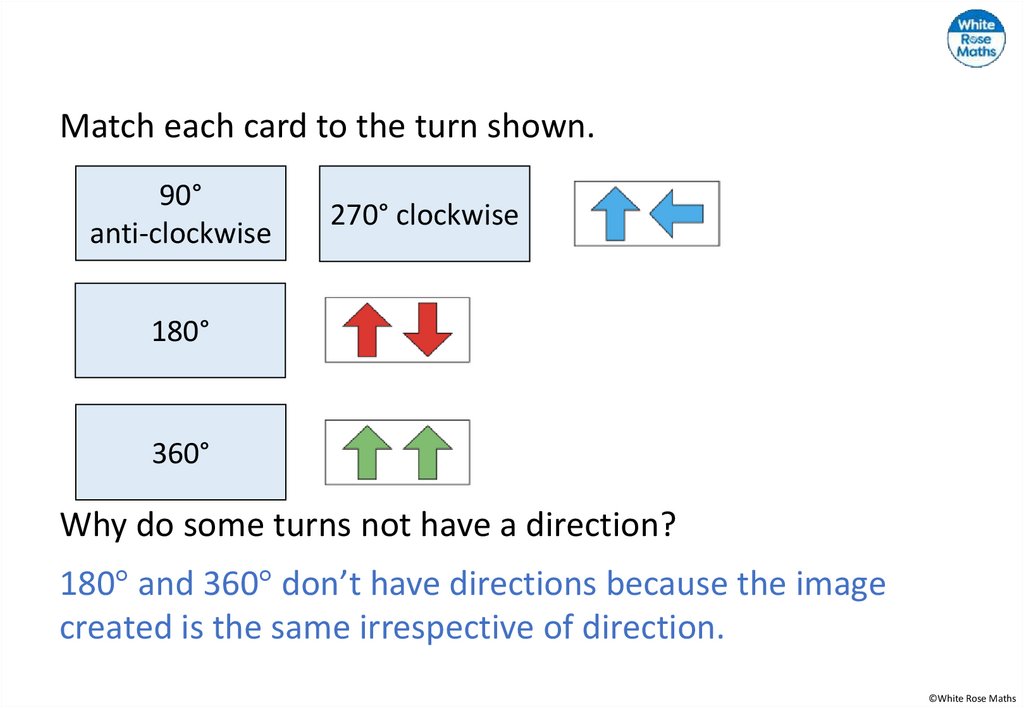
Match each card to the turn shown.90°
anti-clockwise
270° clockwise
180°
360°
Why do some turns not have a direction?
180° and 360° don’t have directions because the image
created is the same irrespective of direction.
©White Rose Maths
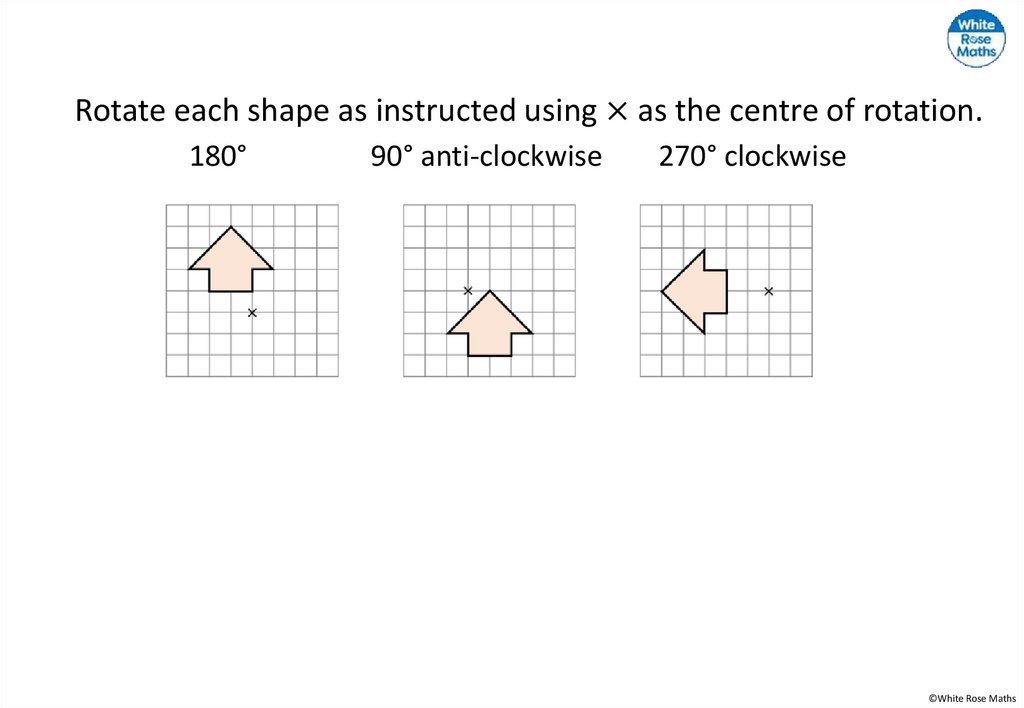
16.
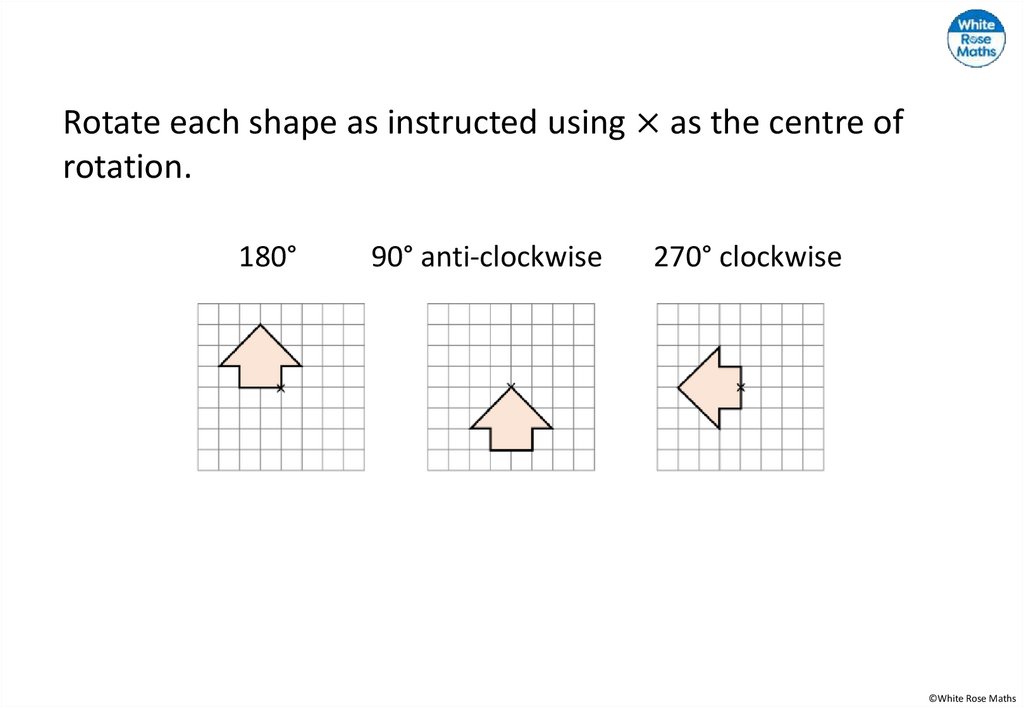
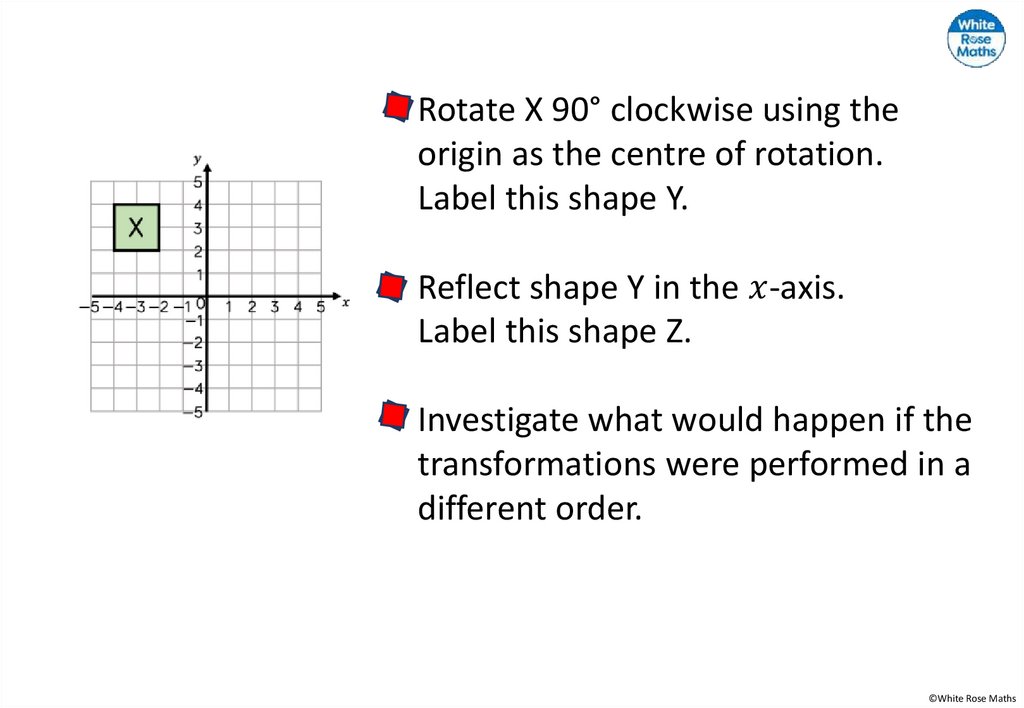
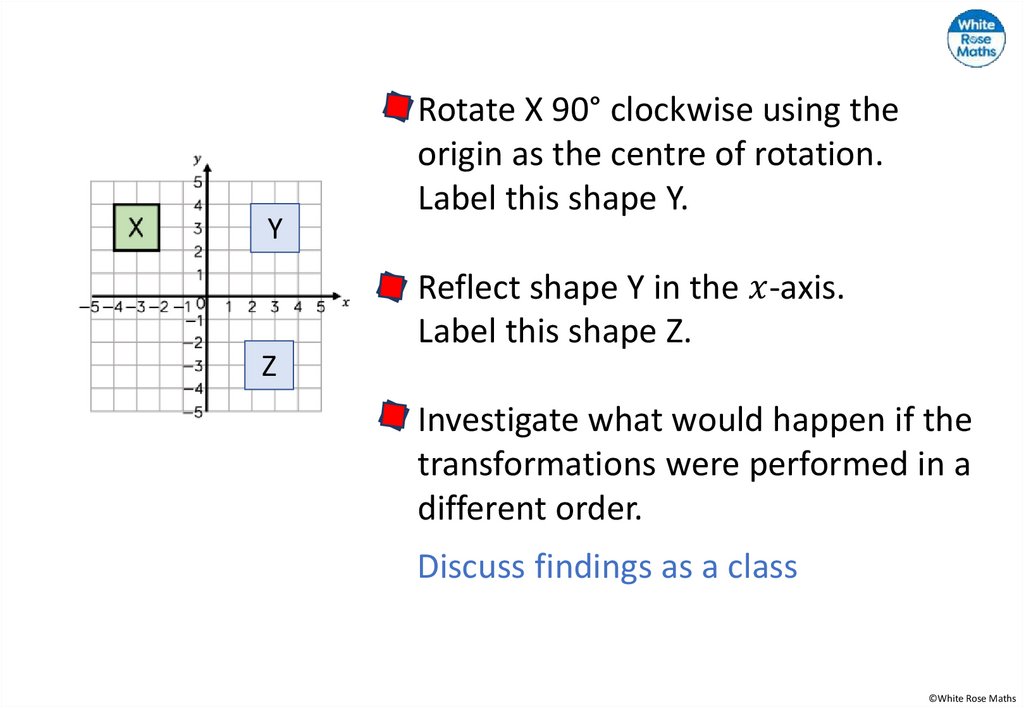
Rotate each shape as instructed using × as the centre ofrotation.
180°
90° anti-clockwise
270° clockwise
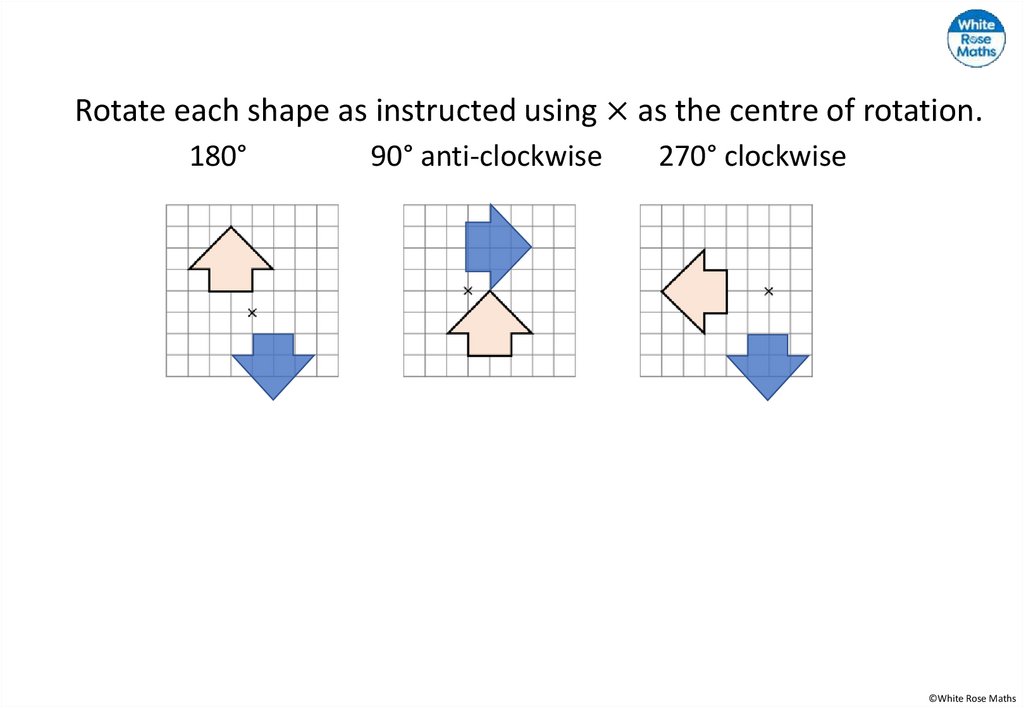
©White Rose Maths
17.
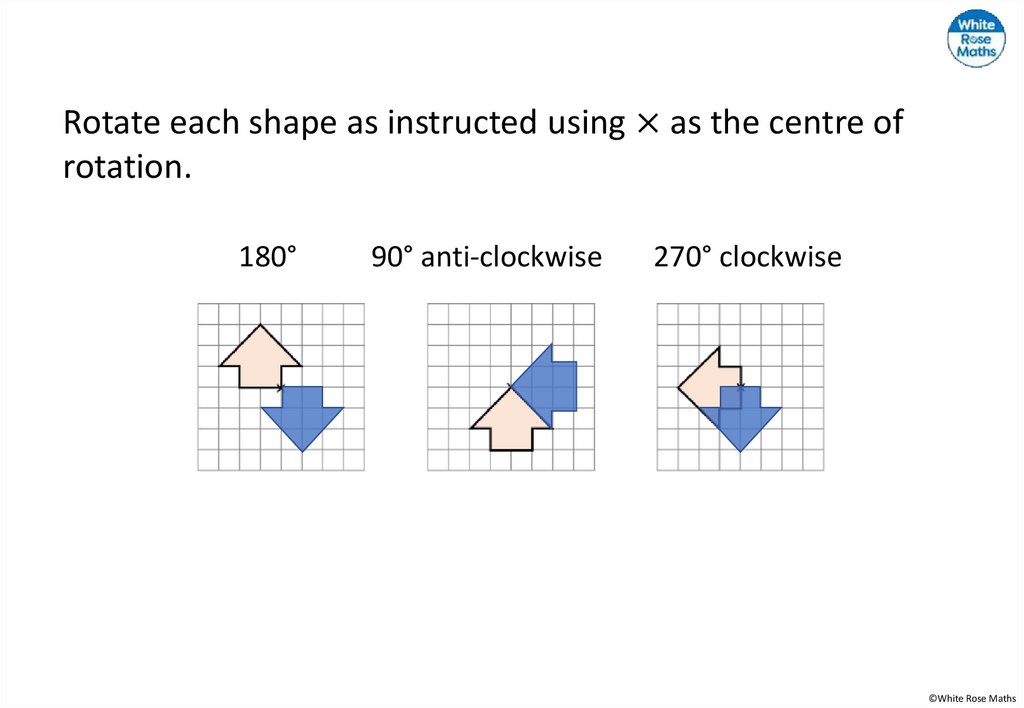
Rotate each shape as instructed using × as the centre ofrotation.
180°
90° anti-clockwise
270° clockwise
©White Rose Maths
18.
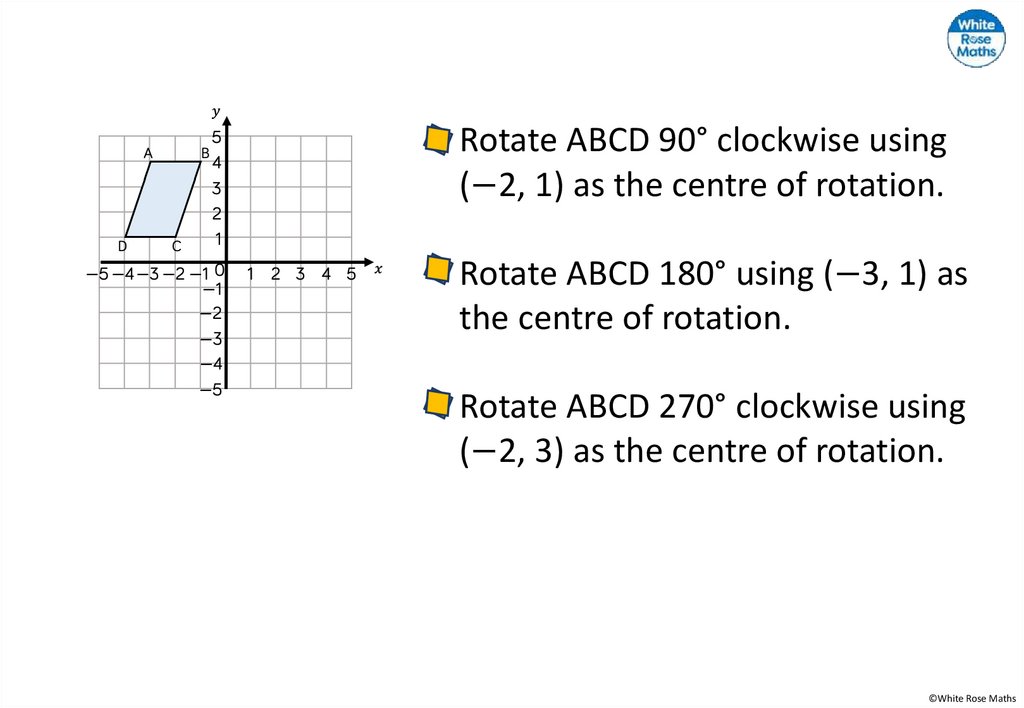
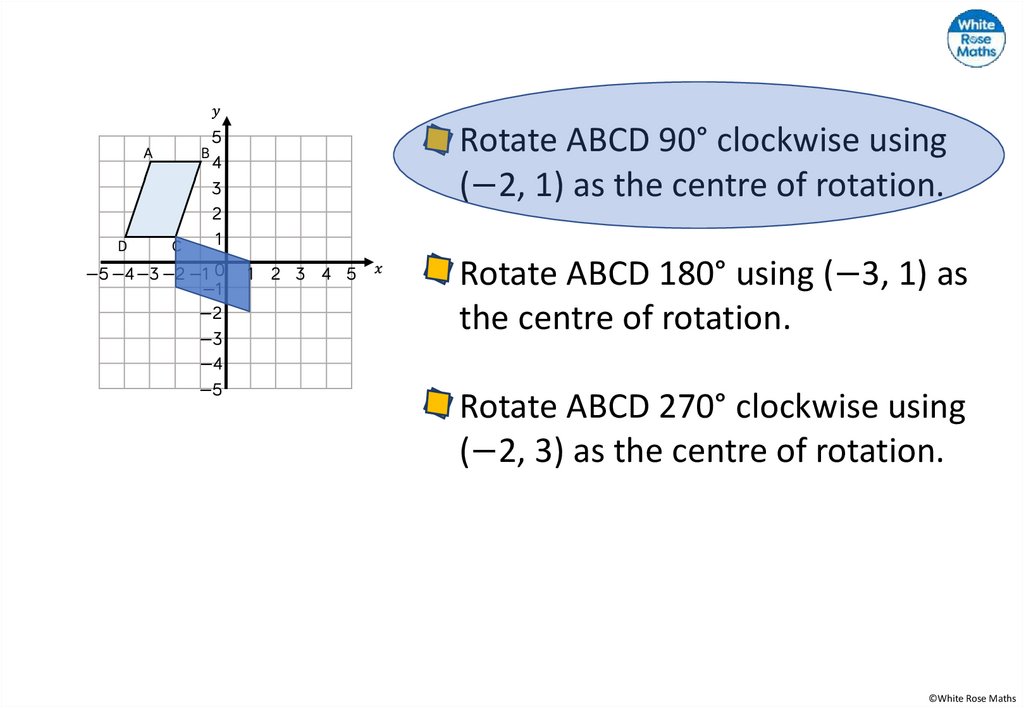
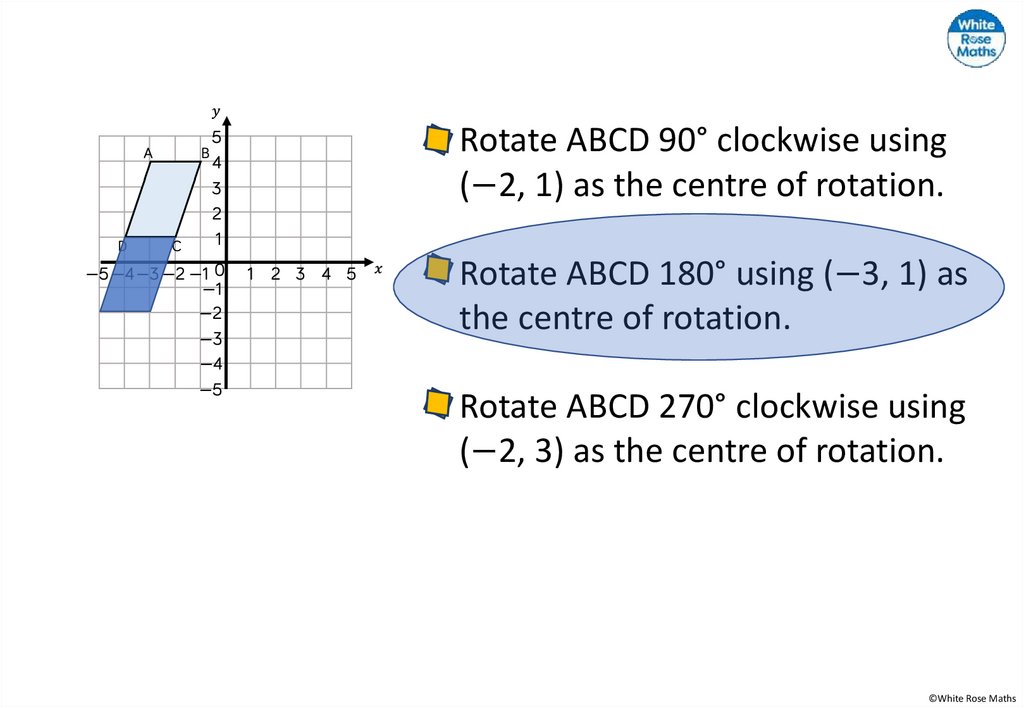
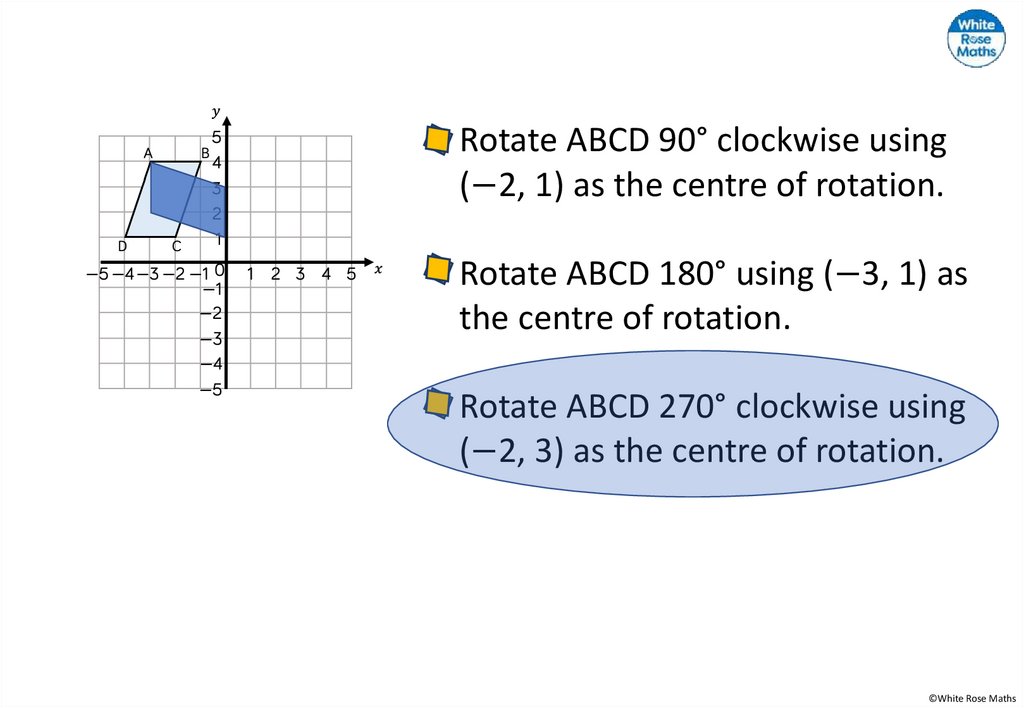
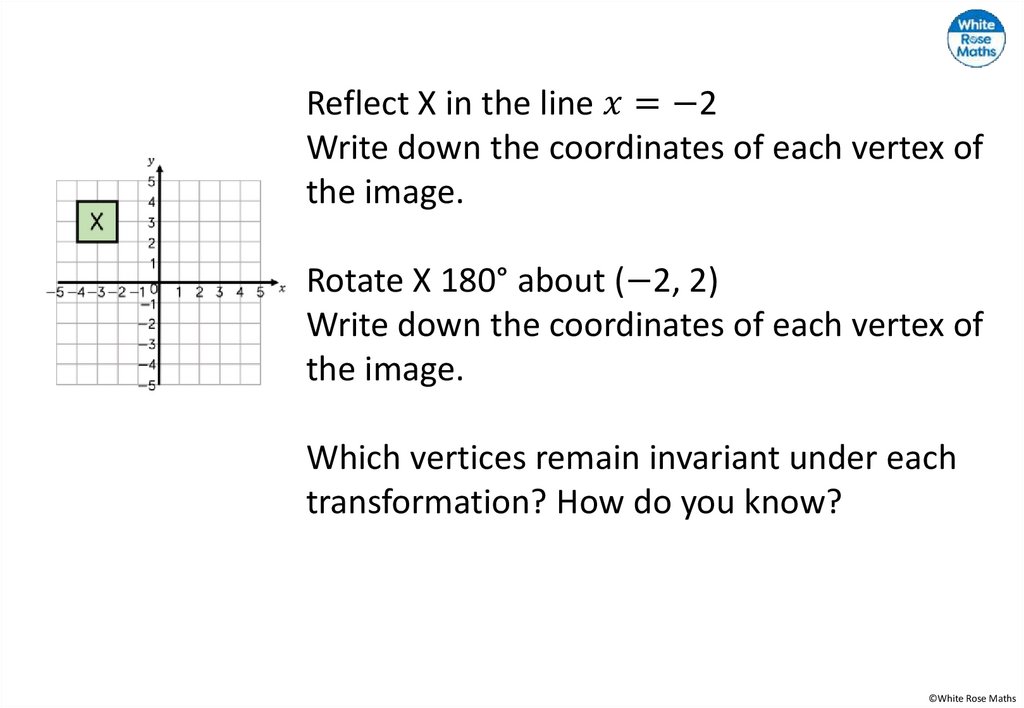
Rotate ABCD 90° clockwise using(−2, 1) as the centre of rotation.
Rotate ABCD 180° using (−3, 1) as
the centre of rotation.
Rotate ABCD 270° clockwise using
(−2, 3) as the centre of rotation.
©White Rose Maths
19.
Rotate ABCD 90° clockwise using(−2, 1) as the centre of rotation.
Rotate ABCD 180° using (−3, 1) as
the centre of rotation.
Rotate ABCD 270° clockwise using
(−2, 3) as the centre of rotation.
©White Rose Maths
20.
Rotate ABCD 90° clockwise using(−2, 1) as the centre of rotation.
Rotate ABCD 180° using (−3, 1) as
the centre of rotation.
Rotate ABCD 270° clockwise using
(−2, 3) as the centre of rotation.
©White Rose Maths
21.
Rotate ABCD 90° clockwise using(−2, 1) as the centre of rotation.
Rotate ABCD 180° using (−3, 1) as
the centre of rotation.
Rotate ABCD 270° clockwise using
(−2, 3) as the centre of rotation.
©White Rose Maths
22.
Rotate each shape as instructed using × as the centre of rotation.180°
90° anti-clockwise
270° clockwise
©White Rose Maths
23.
Rotate each shape as instructed using × as the centre of rotation.180°
90° anti-clockwise
270° clockwise
©White Rose Maths
24.
Rotate ABCD 90° clockwise using(−1, 1) as the centre of rotation.
Rotate ABCD 180° using the
origin as the centre of rotation.
Rotate ABCD 270° clockwise
using (−2, −1) as the centre of
rotation.
©White Rose Maths
25.
Rotate ABCD 90° clockwise using(−1, 1) as the centre of rotation.
Rotate ABCD 180° using the
origin as the centre of rotation.
Rotate ABCD 270° clockwise
using (−2, −1) as the centre of
rotation.
©White Rose Maths
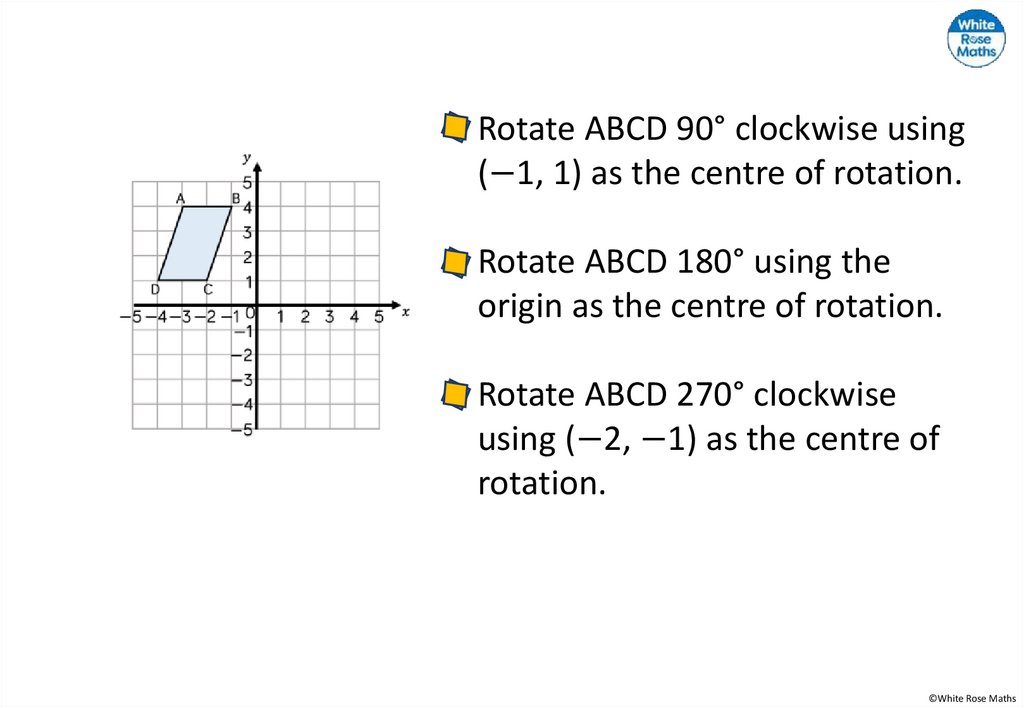
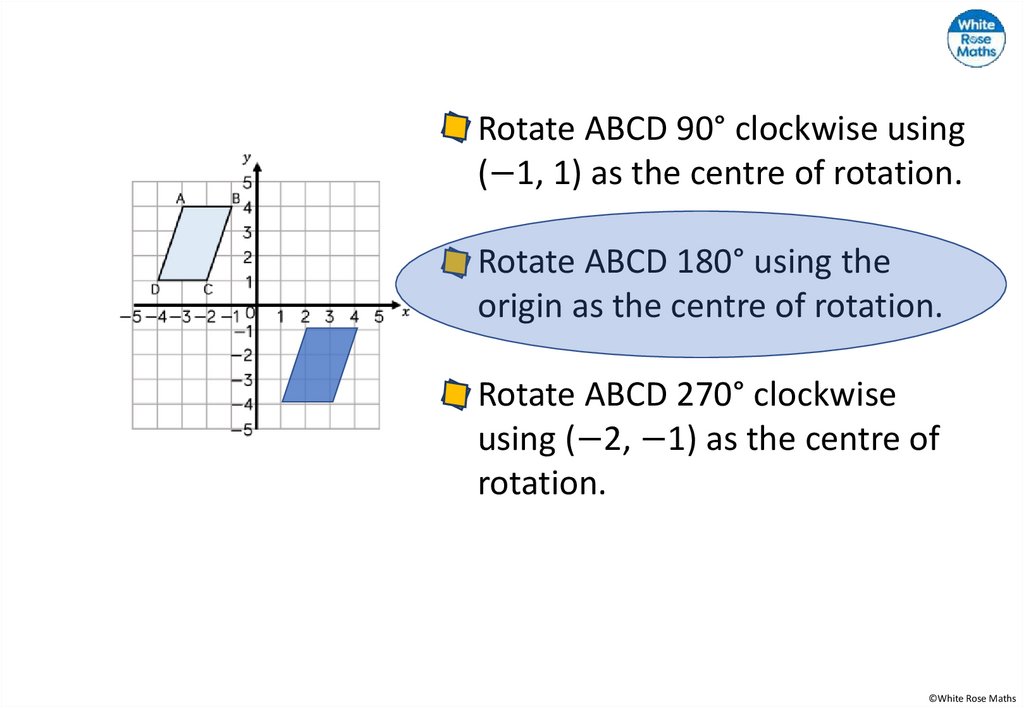
26.
Rotate ABCD 90° clockwise using(−1, 1) as the centre of rotation.
Rotate ABCD 180° using the
origin as the centre of rotation.
Rotate ABCD 270° clockwise
using (−2, −1) as the centre of
rotation.
©White Rose Maths
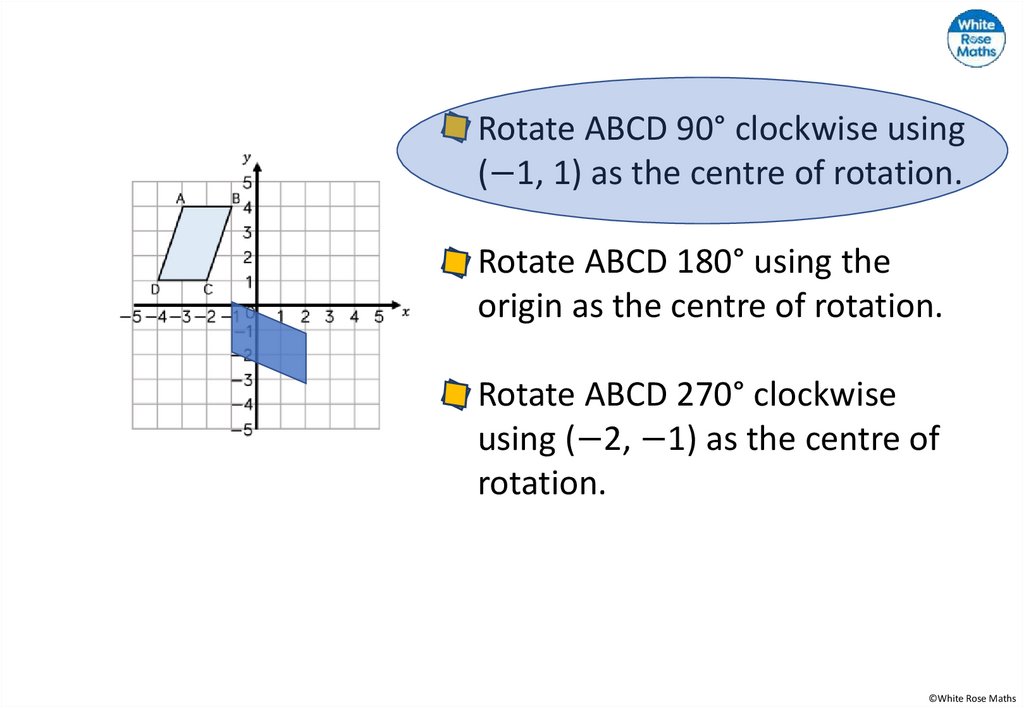
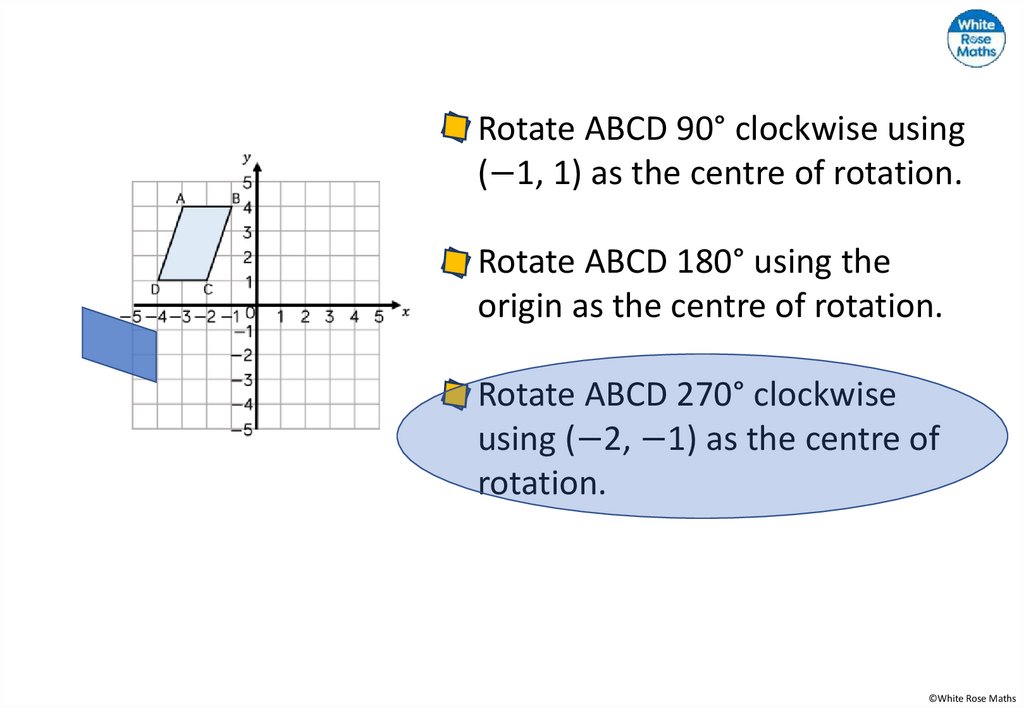
27.
Rotate ABCD 90° clockwise using(−1, 1) as the centre of rotation.
Rotate ABCD 180° using the
origin as the centre of rotation.
Rotate ABCD 270° clockwise
using (−2, −1) as the centre of
rotation.
©White Rose Maths
28.
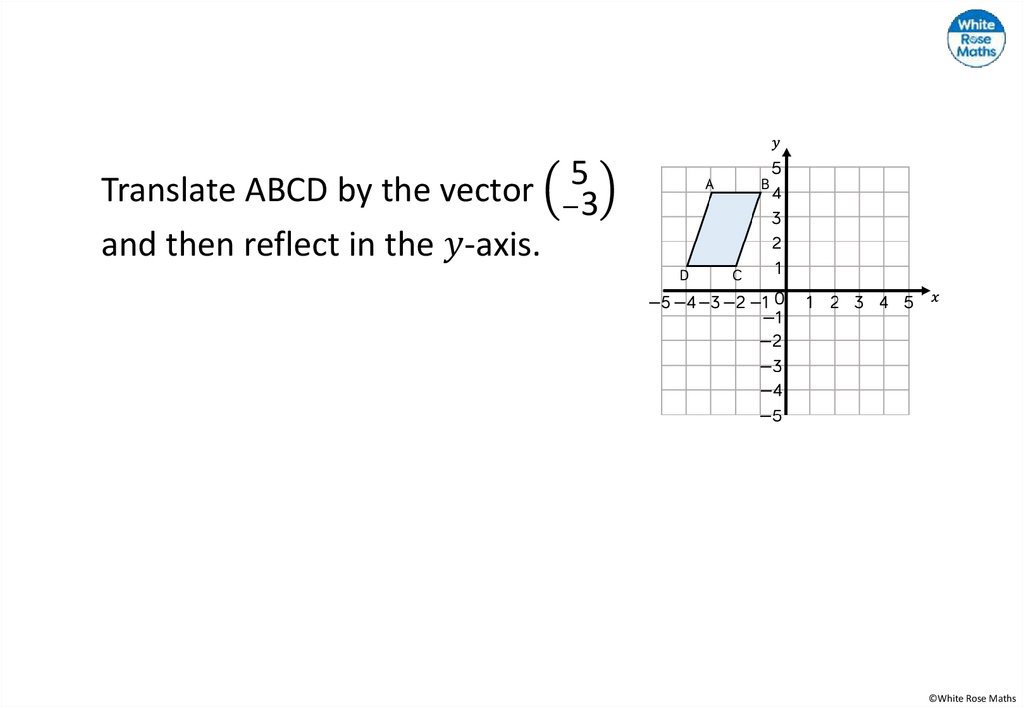
Shape A is an isosceles trapezium with vertices at (0, 3), (0, 9), (4, 4)and (4, 8).
Shape A is rotated 90 degrees anti-clockwise about the origin to give
shape B.
Find the area of shape B. Do you need to perform the rotation?
Find the equation of the line of symmetry of shape B.
©White Rose Maths
29.
Shape A is an isosceles trapezium with vertices at (0, 3), (0, 9), (4, 4)and (4, 8).
Shape A is rotated 90 degrees anti-clockwise about the origin to give
shape B.
Find the area of shape B. Do you need to perform the rotation?
Area = 20 units2 No, you can use the dimensions of shape A
Find the equation of the line of symmetry of shape B.















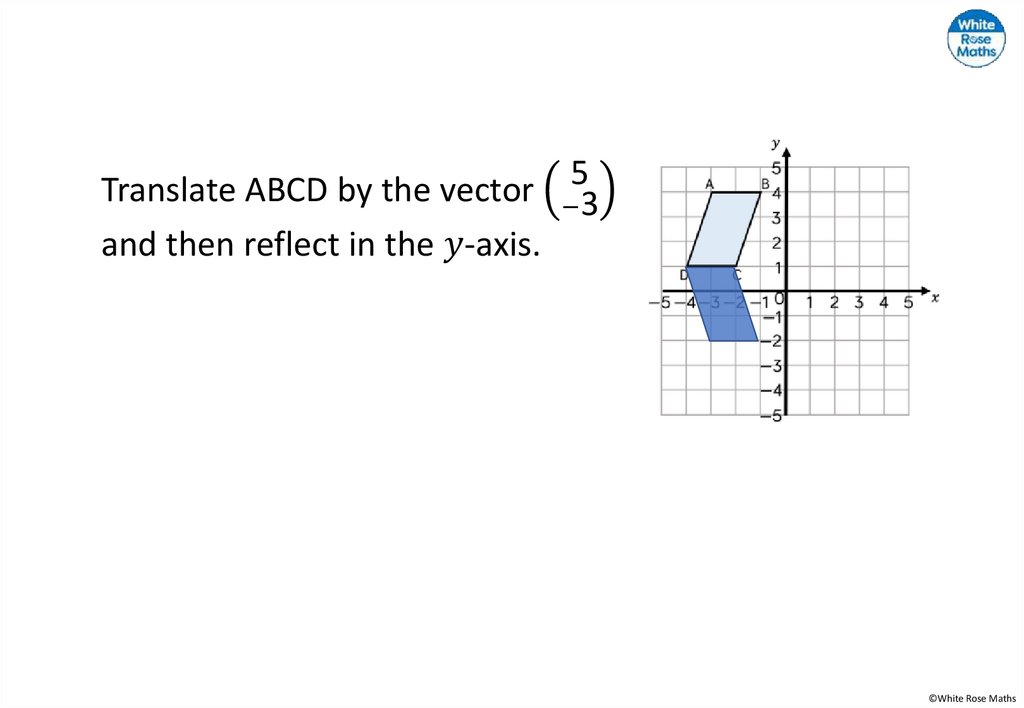


 english
english








