Приложения определенного интеграла

1.

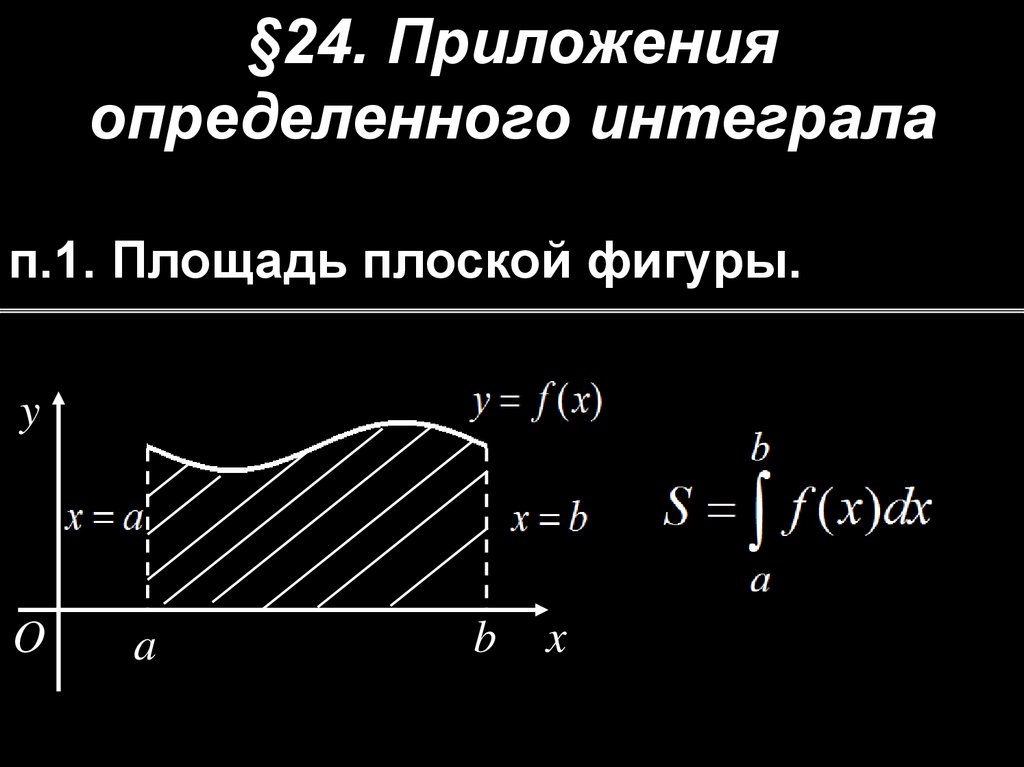
§24. Приложения
определенного интеграла
п.1. Площадь плоской фигуры.
y
O
a
b
x

2.

Теорема 1.
Пусть
функции
отрезке
и
непрерывны на
;
Тогда
площадь S фигуры, заключенной между
графиками
,
,
и
равна

3.

Иллюстрация теоремы 1
y
y
O
O
a
b
x
a
b
x

4.

Иллюстрация теоремы 1
y
b
y
O a
O
b
x
a
x

5.

п.2. Длина дуги кривой.
y
B
A
O
a
b
x
Под длиной дуги AB понимается предел, к
которому стремится длина ломаной,
вписанной в эту дугу, когда число звеньев
ломаной неограниченно возрастает, а длина
наибольшего звена стремится к нулю.

6.

y
O
a
b
x

7.

формула конечных
приращений §9

8.

Длина ломаной:
Длина кривой:

9.

п.3. Объем тела.
S ( x)
a
x x x b
S ( x) — площадь сечения, перпендикулярного
оси Ox, a x b.
V ( x ) — объем части тела, расположенной
левее плоскости S ( x ).

10.

V V ( x x) V ( x) S ( x) x,
dV S ( x)dx,
b
b
a
a
V dV S ( x )dx.

11.

Объем тела вращения
C
y
B
A
O a
D
b
x

12.

Пример. Найти объем тела, полученного
вращением вокруг оси OX области,
2
ограниченной параболой y x и прямыми
x 0, x 1, y 0 .
Решение.
1
1
31
x
V f ( x ) dx x dx
3
0
0
2
2
0
3

13.

п.4. Несобственный интеграл I рода (с
бесконечными пределами
интегрирования).

14.

Пусть функция f (x ) непрерывна
на промежутке [ a ; ).
Несобственным интегралом I рода
f
(
x
)
dx
a
называется предел
b
lim f ( x ) dx.
b
a
b
f ( x)dx lim f ( x)dx
a
b
a

15.

Если предел существует и конечен, то
несобственный интеграл называется
сходящимся (к данному пределу).
Если указанный предел не существует или
бесконечен, то несобственный интеграл
называется расходящимся.

16.

Самостоятельно: дать определение
несобственному интегралу I рода.
b
f
(
x
)
dx
lim
a
b
f
(
x
)
dx
a

17.

c
c
f ( x)dx f ( x)dx f ( x)dx
c
b
lim f ( x ) dx lim f ( x ) dx
a
a
b
c
c R
Несобственный интеграл с двумя
бесконечными пределами сходится лишь
тогда, когда существуют и конечны оба
предела.

18.

Пример. Вычислить или установить
расходимость 0
cos dx.
0
0
cos
dx
lim
cos
dx
lim
sin
x
a
0
a
a
a
lim sin 0 sin a 0 lim sin a
a
a
Интеграл расходится, т.к.
lim sin a
a
не существует.

19.

Несобственный интеграл позволяет придать
смысл такому понятию как площадь
полубесконечной (бесконечной) фигуры.
Пример.
b
dx
dx
1
lim
2
1 x 22 blim
b
x
x 1
1
b
1
lim 1 1
b
b

20.

y
1
y 2
x
O
1
x
1
Кривая y
ограничивает полубесконечную
2
x
фигуру конечной площади
S=1кв.ед.

21.

В курсе теории вероятности встречается
несобственный интеграл Эйлера–Пуассона
e
x2
2
dx.
Можно показать, что
e
x2
2
dx 2 .

22.

Другими словами, площадь S под кривой
x2
2
1
y
e
2
на интервале ( ; ) равна 1кв.ед.
y
1
y
e
2
O
x2
2
x

23.

п.5. Несобственный интеграл II рода
(от неограниченных функций).
Пусть функция f (x ) непрерывна на
промежутке[ a ; b ) и имеет бесконечный разрыв
при x b (неограниченна в точке x b ).
y
y f ( x)
b
O a
b
x

24.

Несобственным интегралом II рода
от функции y f ( x ) на [ a ; b ) называется
предел
b
lim f ( x ) dx.
0
a
b
b
f
(
x
)
dx
lim
f
(
x
)
dx
a
0
a

25.

Если предел существует и конечен, то
несобственный интеграл называется
сходящимся (к данному пределу).
Если указанный предел не существует или
бесконечен, то несобственный интеграл
называется расходящимся.

26.

Самостоятельно: дать определение
несобственному интегралу II рода, если
подынтегральная функция неограниченна в
точке x b.
b
b
a
a
f ( x ) dx
f ( x)dx lim
0

27.

Если функция неограничена (терпит разрыв) в
некоторой внутренней точке c ( a ; b ), то
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
lim
1 0
c 1
f
(
x
)
dx
lim
a
2 0
b
f
(
x
)
dx
c 2
Несобственный интеграл сходится лишь тогда,
когда существуют и конечны оба предела.

28.

Пример. Вычислить или установить
1
расходимость
1
x
dx.
0
1
1
1
dx
dx
lim
lim
2
x
0 x 0 x 0
lim 2 2 2
0

29.

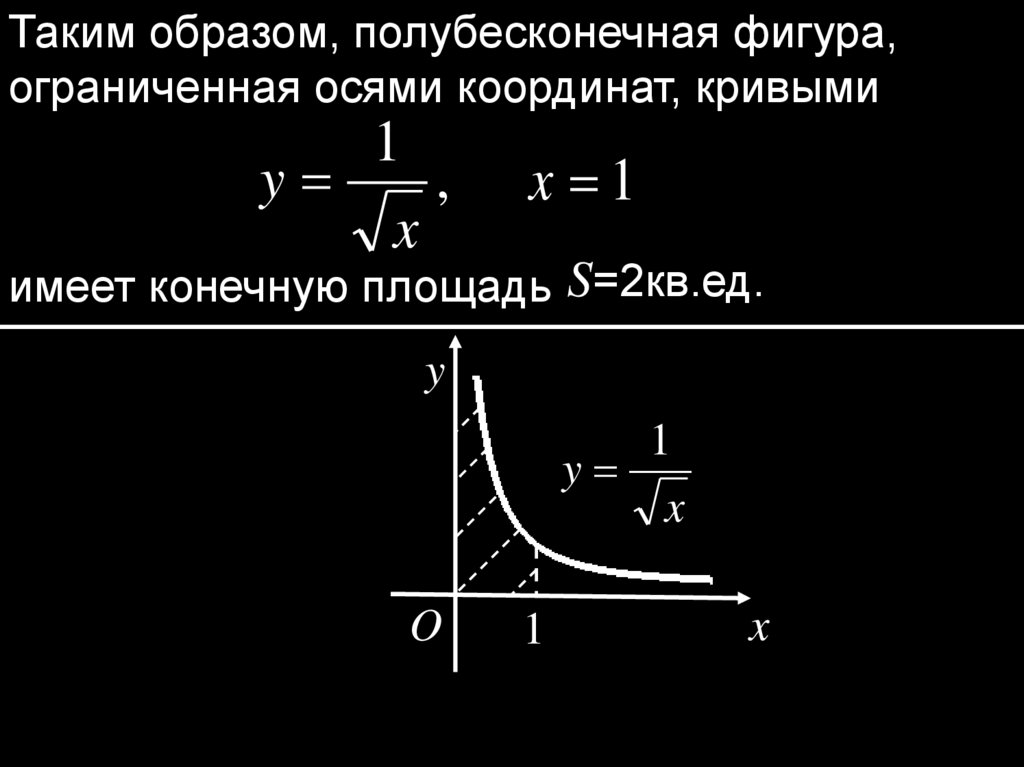
Таким образом, полубесконечная фигура,
ограниченная осями координат, кривыми
1
y
,
x
x 1
имеет конечную площадь S=2кв.ед.
y
1
y
x
O
1
x

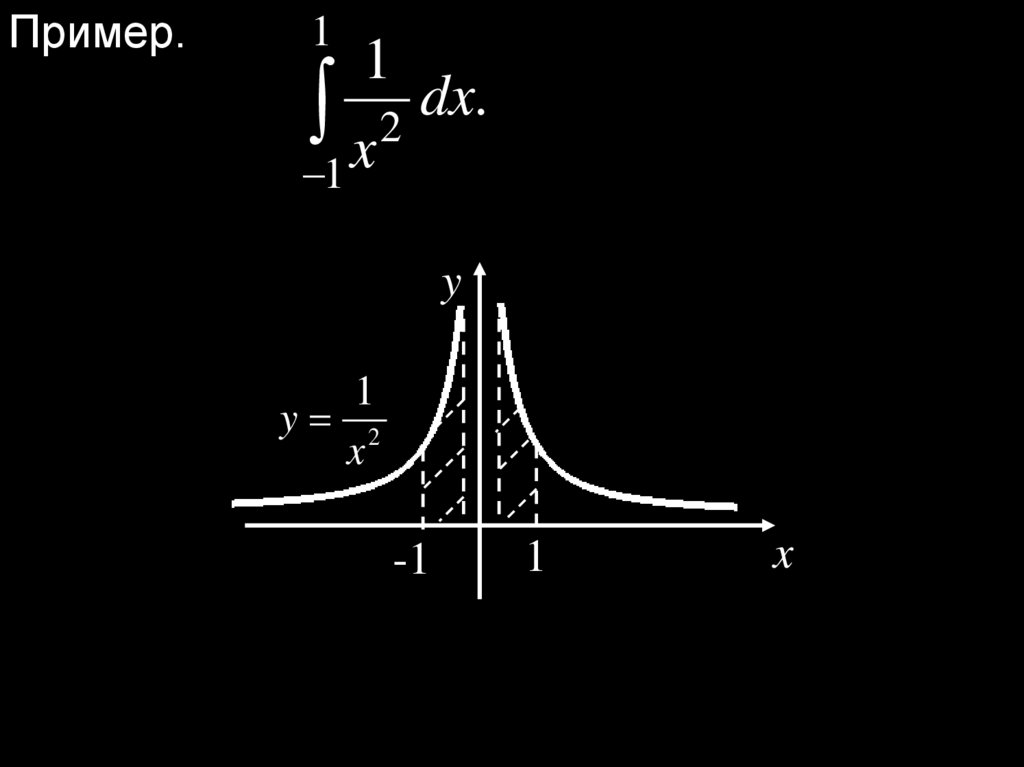
30.

Пример.
1
1
x
1
dx
.
2
y
1
y 2
x
-1
1
x

31.

1
1
x
1
0
dx
2
1
1
1 x
dx
2
0 1
1
0 x
dx
2
1
1
1
dx
lim
dx
2
2
0
0
x
x
lim
1
1
1
2
1
0 2
1
1
lim lim
1 0 x
2 0 x
1
2
1
1
lim 1 lim 1
1 0 1
2 0 2
Несобственный интеграл расходится.