Численные методы минимизации функций одной переменной

1.

Численные методы
минимизации функций
одной переменной

2.

f(x)→min, x U R
x* U - точка абсолютного
(глобального) минимума
f(x*) ≤ f(x)
для всех x U
f * min f ( x) - абсолютный (глобальный) минимум
U
~
x U - точка локального минимума
0 : x U {x : x U , x ~
x }
Глобальный
минимум
f (~
x ) f ( x)
Локальный
минимум

3.

МЕТОДЫ МИНИМИЗАЦИИ
- основанные на вычислении только
значений минимизируемой функции
(прямые)
- использующие значения производных
минимизируемой функции

4.

Метод перебора
f ( x) C[a; b]
0
xi a i(b a) / n,
i 0,...,n
f ( xm ) min f ( xi )
0 i n
n (b a) /
x* xm ,
f * f ( xm )
Пример.
f ( x) x 4 8 x3 6 x 2 72 x на отрезке [1,5; 2]; ε = 0,05
2 1,5
n
10
0,05
xi
f(xi)
xi
f(xi)
1,50
1,55
1,60
1,65
1,70
-89,44 -90,45 -91,24 -91,79 -92,08
1,75
1,80
1,85
1,90
1,95
-92,12 -91,89 -91,37 -90,56 -89,44
х* 1,75,
f* -92,12

5.

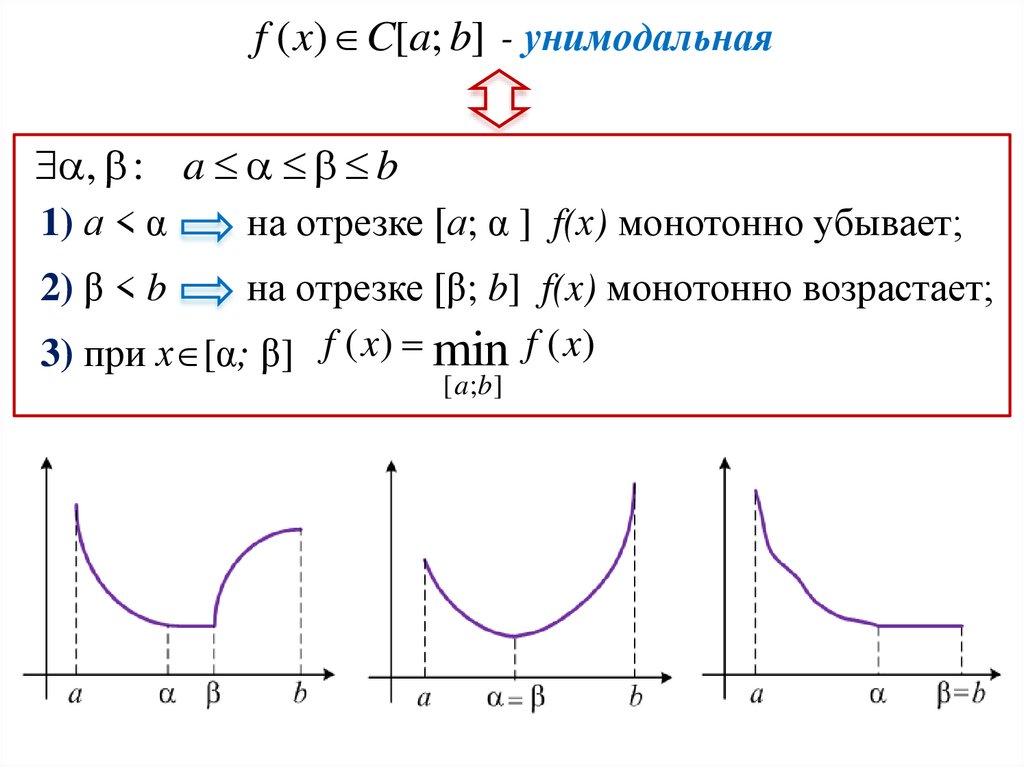
f ( x) C[a; b] - унимодальная
, : a b
1) а < α
на отрезке [а; α ] f(х) монотонно убывает;
2) β < b
на отрезке [β; b] f(x) монотонно возрастает;
3) при х [α; β] f ( x) min f ( x)
[ a ;b ]

6.

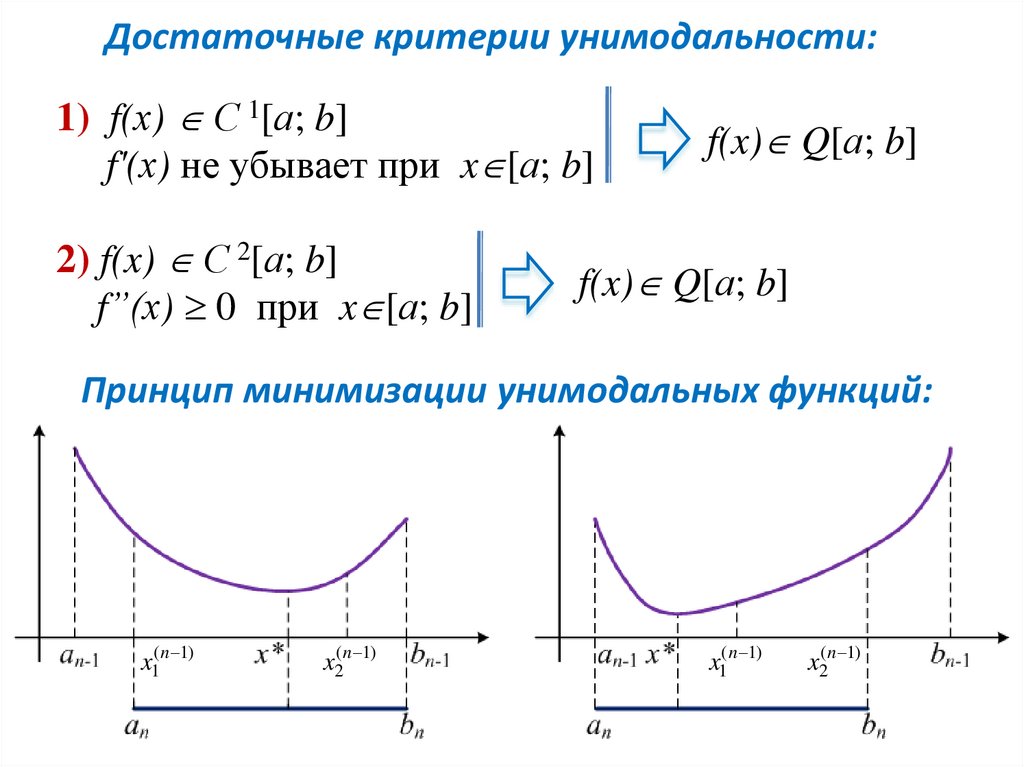
Достаточные критерии унимодальности:
1) f(х) С 1[а; b]
f'(х) не убывает при x [а; b]
2) f(x) С 2[а; b]
f”(х) 0 при x [а; b]
f(x) Q[а; b]
f(x) Q[а; b]
Принцип минимизации унимодальных функций:
x1( n 1)
x2( n 1)
x1( n 1)
x2( n 1)

7.

Метод деления пополам
f ( x) Q[a; b]
0
(0; 2 )
a0 a; b0 b
an 1 bn 1
( n 1)
x1
;
2
an 1 bn 1
( n 1)
x2
2
f ( x1( n 1) ) f ( x2( n 1) )
( n 1)
an an 1, bn x2
f ( x1( n 1) ) f ( x2( n 1) )
an x1( n 1) , bn bn 1
x* (bn an ) / 2
n (bn an ) / 2 (b a ) / 2n 1 / 2

8.

Пример.
f ( x) x 8 x 6 x 72 x на отрезке [1,5; 2]; ε = 0,05
= 0,02 < 2 = 0,1
n
an
4
3
2
bn
n
x1( n )
x2( n ) f ( x1( n ) ) f ( x2( n ) )
Примечание
( 0)
( 0)
f
(
x
)
f
(
x
0 1,50 2,00 0,25 1,74 1,76 -92,135 -92,096
1
2 )
1 1,50 1,76 0,13 1,62 1,64 -91,487 -91,696
f ( x1(1) ) f ( x2(1) )
2 1,62 1,76 0,07 1,68 1,70 -91,995 -92,084
f ( x1( 2) ) f ( x2( 2) )
3 1,68 1,76 0,04
3 , точность
достигнута
х* 1,72
f* f (1,72) = -92,13

9.

Метод золотого сечения
x - точка золотого сечения отрезка [а; b]:
b a b x
b x x a
3 5
x1 a
(b a ),
2
5 1
x2 a
(b a)
2
x1 a b x2
x2 a b x1

10.

f ( x) Q[a; b]
0
a1 a; b1 b
x1( n 1) , x2( n 1) - точки золотого сечения отрезка [an 1; bn 1 ]
f ( x1( n 1) ) f ( x2( n 1) )
( n 1)
an an 1, bn x2 ,
( n 1)
xn x1
( n 1)
( n 1)
f ( x1
) f ( x2 )
( n 1)
an x1 , bn bn 1,
( n 1)
xn x2
n
5 1
(b a)
x * xn n
2
5 1
n ln
2,1 ln
ln
b a
b a
2

11.

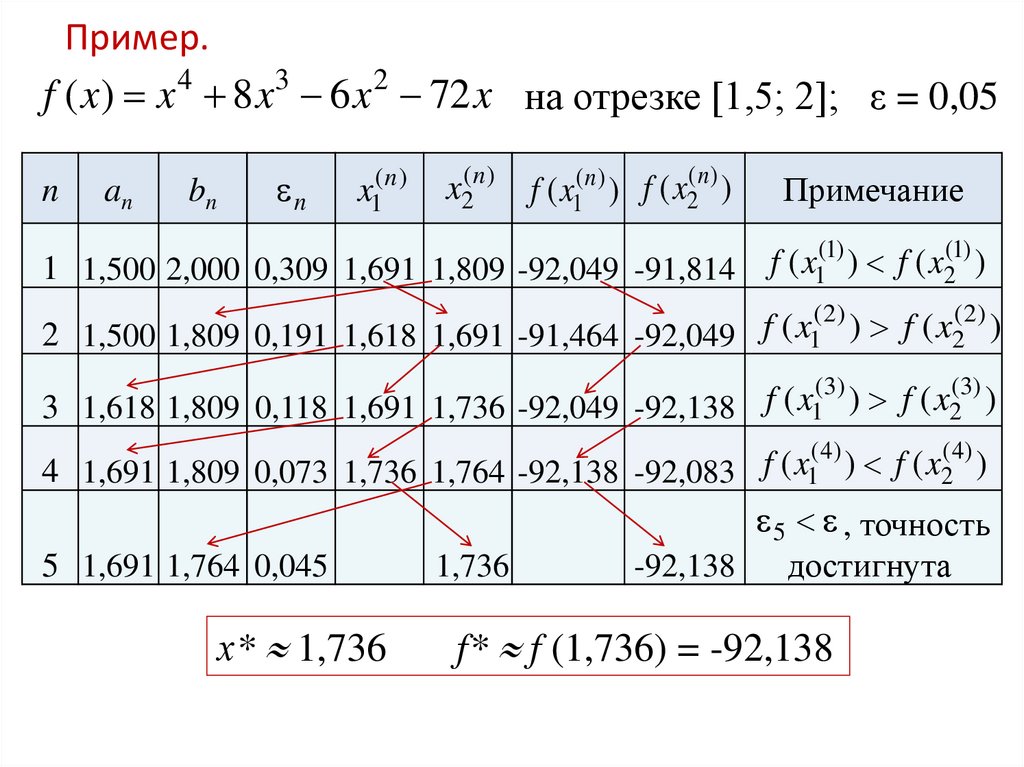
Пример.
f ( x) x 8 x 6 x 72 x на отрезке [1,5; 2]; ε = 0,05
4
3
2
bn
n
x1( n )
x2( n ) f ( x1( n ) ) f ( x2( n ) )
Примечание
1 1,500 2,000 0,309 1,691 1,809 -92,049 -91,814
f ( x1(1) ) f ( x2(1) )
n
an
( 2)
( 2)
f
(
x
)
f
(
x
2 1,500 1,809 0,191 1,618 1,691 -91,464 -92,049
1
2 )
( 3)
( 3)
f
(
x
)
f
(
x
3 1,618 1,809 0,118 1,691 1,736 -92,049 -92,138
1
2 )
( 4)
( 4)
f
(
x
)
f
(
x
4 1,691 1,809 0,073 1,736 1,764 -92,138 -92,083
1
2 )
5 , точность
5 1,691 1,764 0,045
достигнута
1,736
-92,138
х* 1,736
f* f (1,736) = -92,138

12.

Метод ломаных
f(х) удовлетворяет на отрезке [а; b] условию Липшица:
L 0 x' , x" [a; b] :
f(х) С 1[а; b]
f ( x' ) f ( x") L x' x"
L max f ' ( x)
[ a;b ]
sin x
на отрезке [10; 15]
f ( x)
x
x cos x sin x x cos x sin x x 1
f ' ( x)
2 0,11
2
2
x
x
x
Пример.
L = 0,11

13.

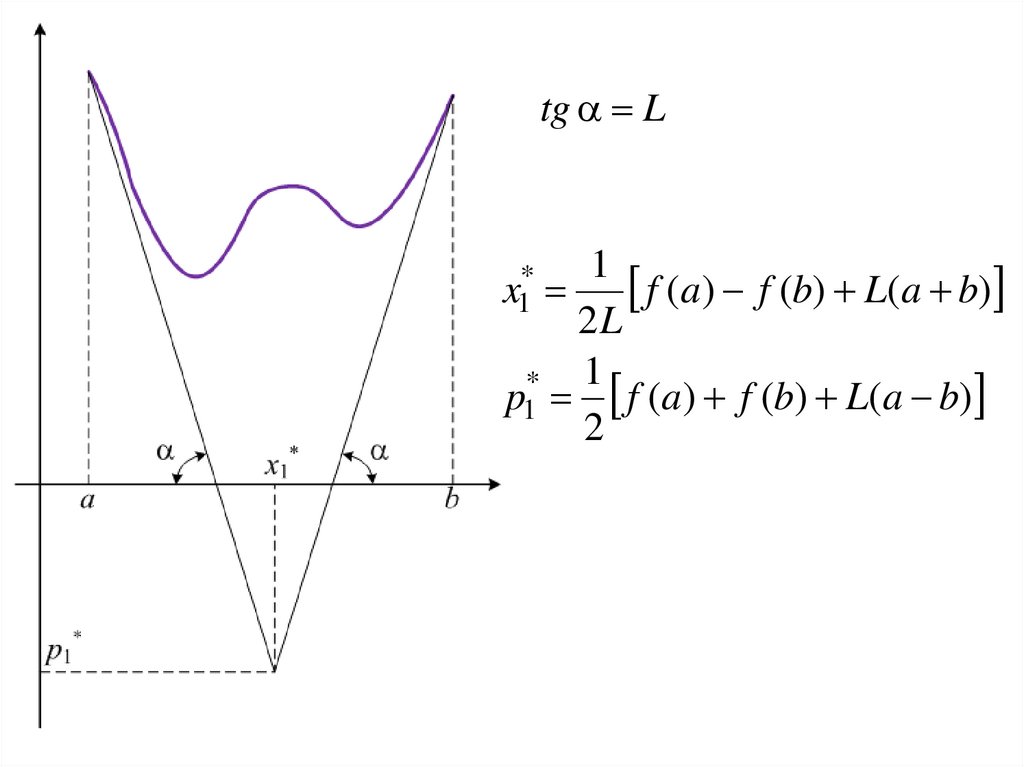
tg L
1
f (a) f (b) L(a b)
2L
* 1
p1 f (a) f (b) L(a b)
2
x1*

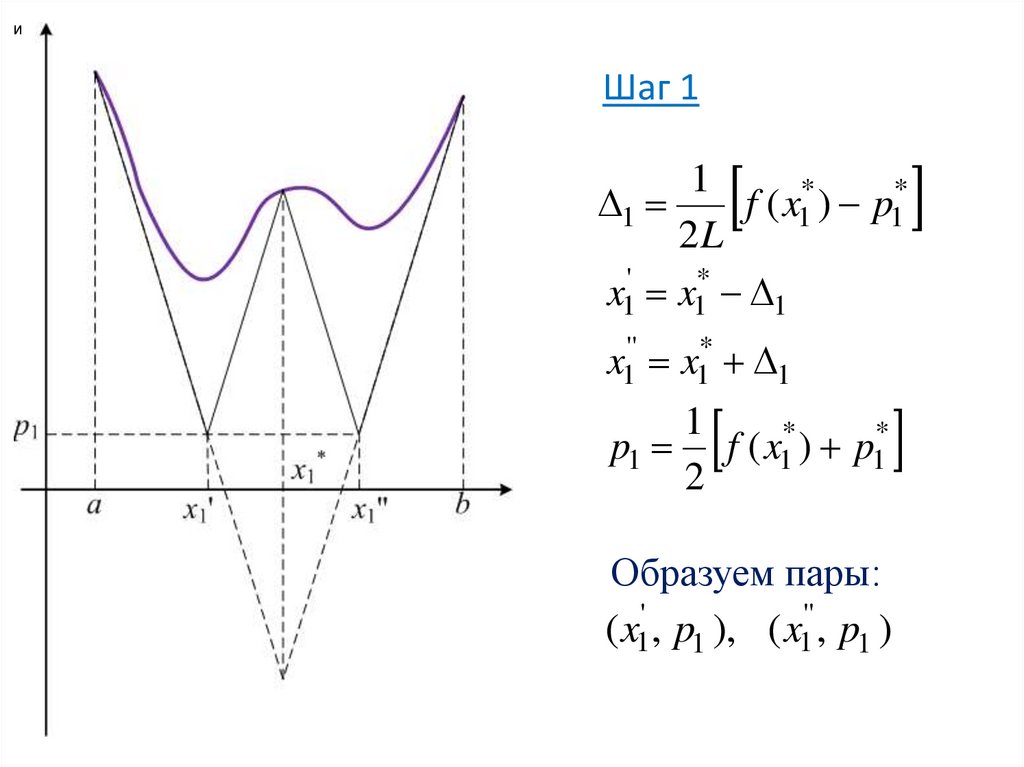
14.

и
Шаг 1
1
1
f ( x1* ) p1*
2L
x1' x1* 1
x1'' x1* 1
1
p1 f ( x1* ) p1*
2
Образуем пары:
( x1' , p1 ), ( x1'' , p1 )

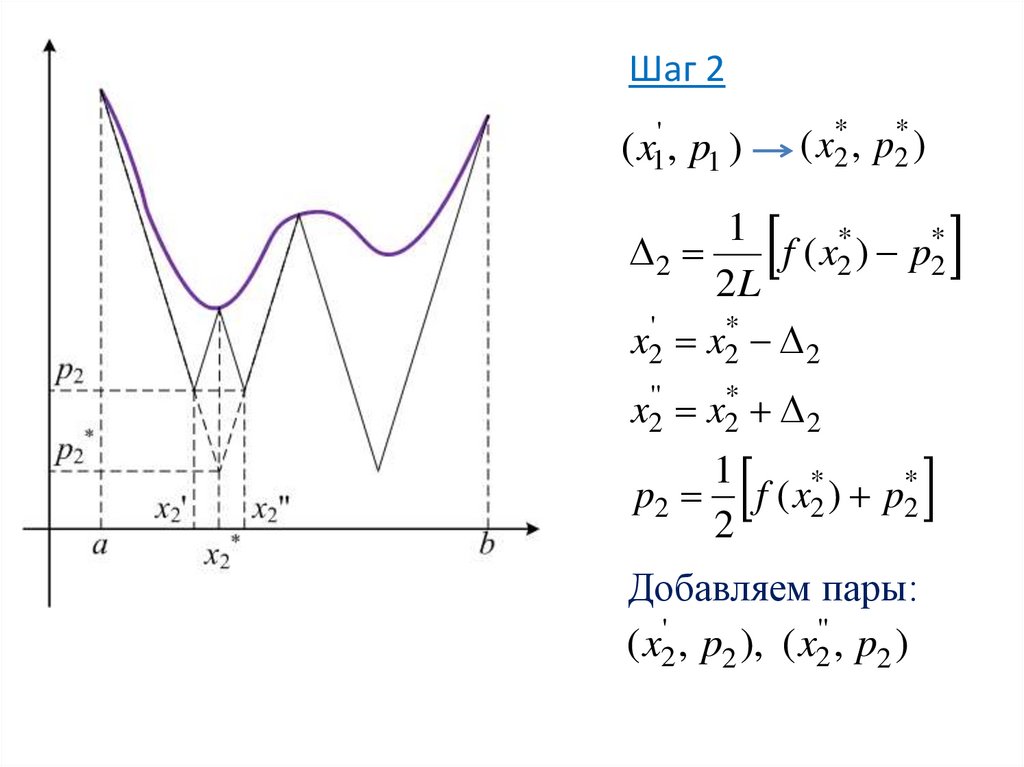
15.

Шаг 2
( x2* , p2* )
( x1' , p1 )
1
2
f ( x2* ) p2*
2L
x2' x2* 2
x2'' x2* 2
1
p2 f ( x2* ) p2*
2
Добавляем пары:
( x2' , p2 ), ( x2'' , p2 )

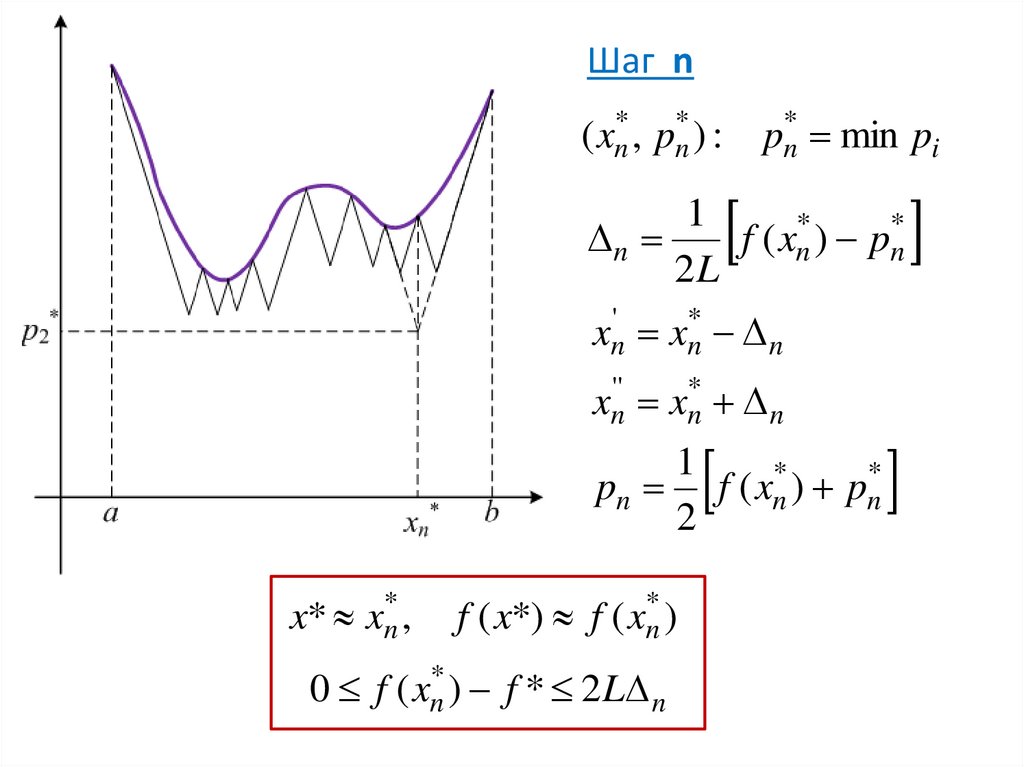
16.

Шаг n
pn* min pi
( xn* , pn* ) :
1
n
f ( xn* ) pn*
2L
xn' xn* n
xn'' xn* n
1
pn f ( xn* ) pn*
2
x* xn* ,
f ( x*) f ( xn* )
0 f ( xn* ) f * 2 L n

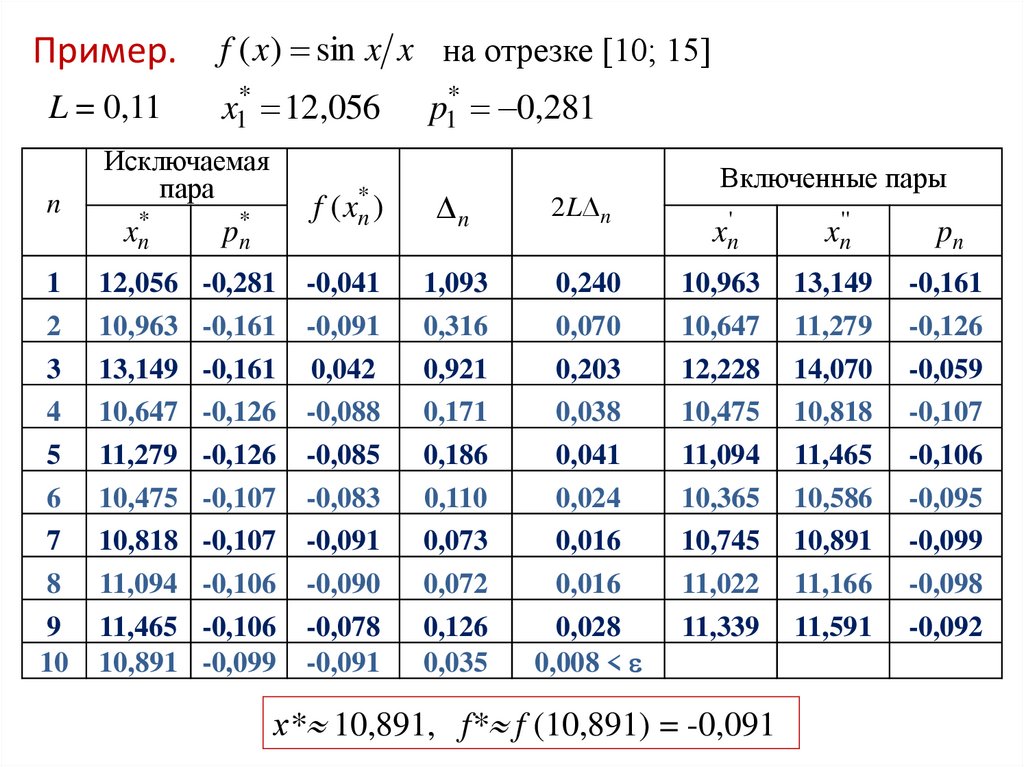
17.

Пример.
f ( x) sin x x на отрезке [10; 15]
L = 0,11
x1* 12,056
n
Исключаемая
пара
xn*
pn*
p1* 0,281
Включенные пары
f ( xn* )
n
2 L n
xn'
xn''
pn
1
12,056 -0,281
-0,041
1,093
0,240
10,963
13,149
-0,161
2
10,963 -0,161
-0,091
0,316
0,070
10,647
11,279
-0,126
3
13,149 -0,161
0,042
0,921
0,203
12,228
14,070
-0,059
4
10,647 -0,126
-0,088
0,171
0,038
10,475
10,818
-0,107
5
11,279 -0,126
-0,085
0,186
0,041
11,094
11,465
-0,106
6
10,475 -0,107
-0,083
0,110
0,024
10,365
10,586
-0,095
7
10,818 -0,107
-0,091
0,073
0,016
10,745
10,891
-0,099
8
11,094 -0,106
-0,090
0,072
0,016
11,022
11,166
-0,098
9
10
11,465 -0,106
10,891 -0,099
-0,078
-0,091
0,126
0,035
0,028
0,008 <
11,339
11,591
-0,092
х* 10,891, f* f (10,891) = -0,091

18.

Mетод касательных
f (х) - выпуклая на отрезке [а; b]
f ( x' ) (1 ) f ( x' ' )
: 0 1 x' , x" [a; b]
f x' (1 ) x' ' f ( x' ) (1 ) f ( x' ' )
x' (1 ) x' '
Критерий выпуклости:
f (x) С 2[а; b]
f (х) – выпуклая
f x' (1 ) x' '
x [a; b]
f " ( x) 0

19.

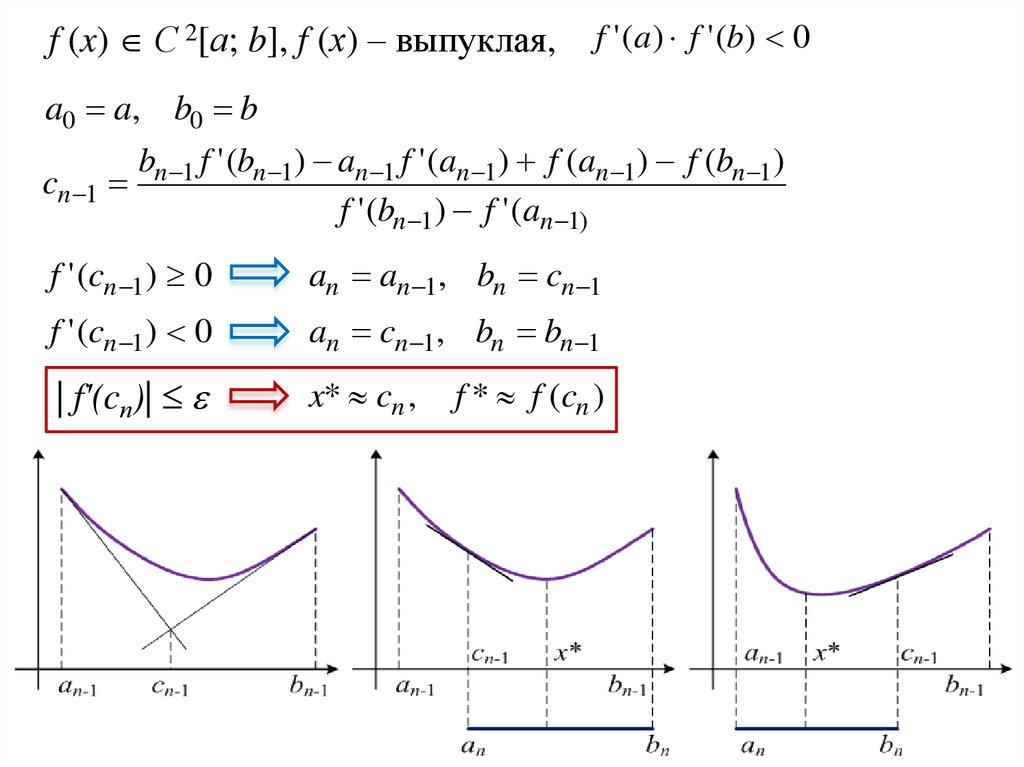
f (x) С 2[а; b], f (х) – выпуклая,
f ' (a) f ' (b) 0
a0 a, b0 b
bn 1 f ' (bn 1) an 1 f ' (an 1) f (an 1 ) f (bn 1)
cn 1
f ' (bn 1) f ' (an 1)
f ' (cn 1) 0
an an 1, bn cn 1
f ' (cn 1) 0
an cn 1, bn bn 1
| f'(cп)|
x* cn ,
f * f (cn )

20.

2
x
f
(
x
)
x
e
на отрезке [-1; 1]; ε = 0,05
Пример.
f ' ' ( x) 2 e x 0
f ' ( x) 2 x e x
f ' ( 1) f ' (1) 1,632 4,718 0
n
an
bn
f(an)
f(bn)
f'(an) f'(bn)
cn
f'(cn)
Примечание
0 -1,00000 1,00000 1,368 3,718 -1,632 4,718 0,11586 1,355
f ' (c0 ) 0
1 -1,00000 0,11586 1,368 1,136 -1,632 1,355 -0,41637 -0,173
f ' (c1) 0
2 -0,41637 0,11586 0,833 1,136 -0,173 1,355 -0,14313 0,580
f ' (c2 ) 0
3 -0,41637 -0,14313 0,833 0,887 -0,173 0,580 -0,27804 0,201
f ' (c3 ) 0
4 -0,41637 -0,27804 0,833 0,835 -0,173 0,201 -0,34679 0,013
| f'(cп)|
х* -0,347; f* f (-0,347)= 0,827

21.

Метод Ньютона
f (x) С 2[а; b], f (х) – выпуклая
Отыскание корней:
Минимизация:
f ( x) 0
f ' ( x) 0
f ( xn 1 )
xn xn 1
f ' ( xn 1 )
f ' ( xn 1 )
xn xn 1
f ' ' ( xn 1 )
| f '(хп)|
f ' ' ( x) 0
L
q 2 f ' ( x0 ) 1
2
õ* xn , f * f ( xn )
2 2n
x * xn
q , n 1,2,...
L

22.

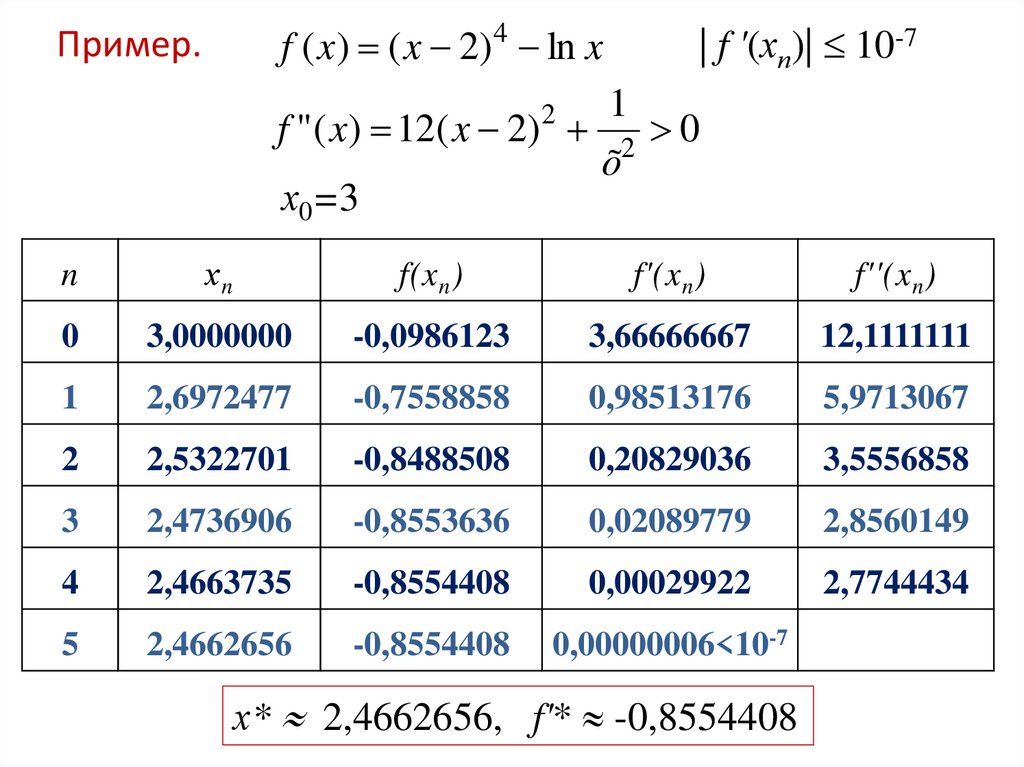
f ( x) ( x 2) 4 ln x
Пример.
| f '(хп)| 10-7
1
f " ( x) 12( x 2) 2 0
õ
х0=3
2
n
хn
f(x n )
f'(x n )
f''(x n )
0
3,0000000
-0,0986123
3,66666667
12,1111111
1
2,6972477
-0,7558858
0,98513176
5,9713067
2
2,5322701
-0,8488508
0,20829036
3,5556858
3
2,4736906
-0,8553636
0,02089779
2,8560149
4
2,4663735
-0,8554408
0,00029922
2,7744434
5
2,4662656
-0,8554408
0,00000006<10-7
х* 2,4662656, f'* -0,8554408