Similar presentations:
Наибольшее, наименьшее значение функции
1.
Наибольшее, наименьшее значениефункции
Хомкина Н.Н., учитель математики
МОУ Нижнебузулинская СОШ
Свободненского района Амурской области
2.
Задание 11Найти точку максимума
или минимума функции
Найти наибольшее или
наименьшее значение функции
Два прототипа
Сначала необходимо понять, что именно от нас
хотят в задании. Многие ученики путают понятия
«точка максимума / минимума» и «наибольшее /
наименьшее значение». Дело в том, что точка
экстремума – это x, а наибольшее или наименьшее
значение – это у. Как не запутаться? Обрати
внимание на слово-маркер «точка». Если ты
видишь его, то речь идет об х, если этого слова нет,
то речь об у.
3.
Алгоритм1) Находим производную
2) Находим точки экстремума: приравниваем
производную к нулю
3) На координатной прямой
отмечаем точки, сверху
описываем производную,
снизу функцию.
4) Находим знаки
производной в интервалах
между корнями.
5) Определяем вид каждого
экстремума
3) Считаем значение исходной
функции
- в начале промежутка
- в конце промежутка
-в экстремумах [a ; b], если
есть
4) Выбираем нужное значение.
В ответ – значение ФУНКЦИИ
4.
Задача.Найдите наименьшее значение функции
у= х3 – 27 х на отрезке [0; 4]
Решение.
у’ (х) = 3х2 – 27
3х2 – 27 = 0
х1 = 3
х2 = - 3
Или
у(0) = 0
у(3) = -54
Ответ: - 54
у(4) = - 44
5.
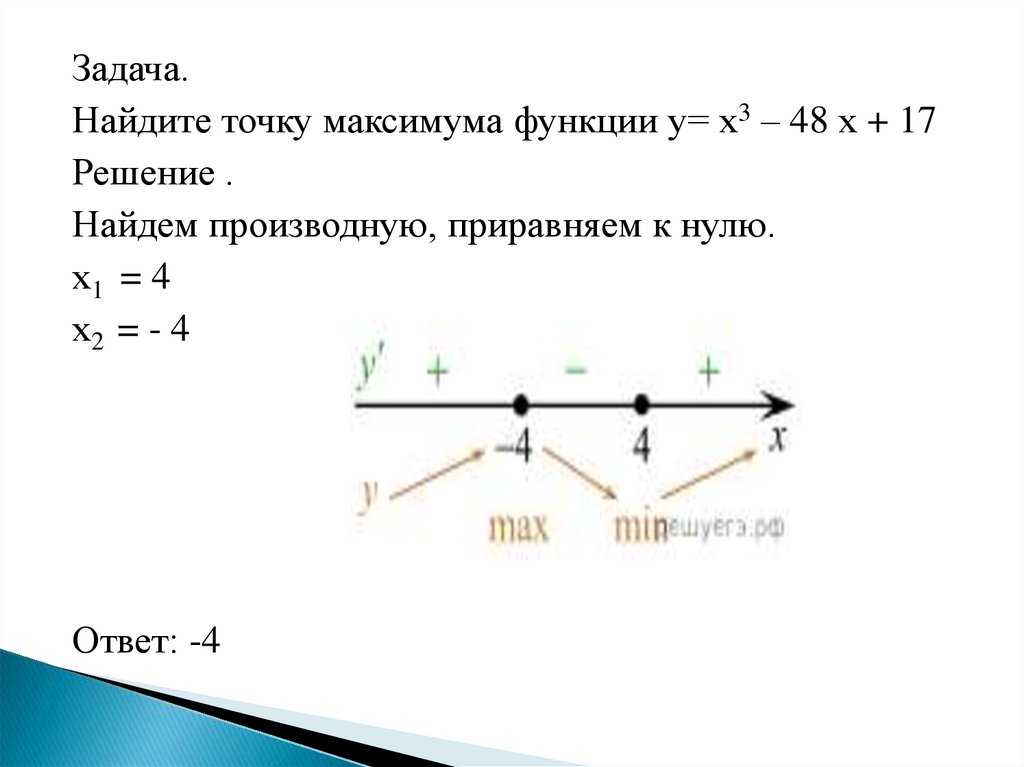
Задача.Найдите точку максимума функции у= х3 – 48 х + 17
Решение .
Найдем производную, приравняем к нулю.
х1 = 4
х2 = - 4
Ответ: -4
6.
1.Найдите наименьшее значение функции
y = 15 + 12x + x 3 на отрезке [−2; 2].
Ответ: - 17
2. Найдите точку максимума функции
y = x 5+15 x 3 - 260 х
Ответ: -2
3. Найдите точку максимума функции
у = (х – 2)2 е х-6
Ответ: 0
4. Найдите наибольшее значение функции
у = (8 - х)е х-7 на отрезке [3; 10]
Ответ: 1
7.
5. Найдите наибольшее значение функцииу= ln (x + 5)5 – 5x на отрезке [- 4,5; 0]
Ответ: 20
6. Найдите точку минимума функции
у =3х - ln (x + 3)3
Ответ: -2
7. Найдите точку минимума функции
у = 2х2 - 5х + ln х -3
Ответ: 1
8. Найдите наименьшее значение функции
у = 4х2 - 10х + 2ln х -5 на отрезке [0,3; 3]
Ответ:-11
8.
9. Найдите наименьшее значение функцииу = 3 + 5π/4 – 5х – 5√2 cos x на отрезке [0; π/2]
Ответ: -2
10. Найдите наименьшее значение функции
у = 5cos x – 6х + 4 на отрезке [π/2; 0]
Ответ: 9
11. Найдите наибольшее значение функции
у = 15х – 3 sin x + 5 на отрезке [ -π/2; 0]
Ответ: 5
12. Найдите наибольшее значение функции
у = 3 tg x -3х + 5 на отрезке [ -π/4; 0]
Ответ: 5









 mathematics
mathematics








